Похожие презентации:
Численные методы механики сплошных сред. Метод граничных интегральных уравнений для задач гидромеханики
1. «Численные методы механики сплошных сред. Метод граничных интегральных уравнений для задач гидромеханики»
Лекция 52. Решение задачи обтекания тела вращения с использованием МДВ
Краевая задача обтекания тела набегающим потоком для функции токав осевой плоскости течения, может быть сформулирована следующим образом:
xx yy y / y 0 в области
~ y1 /(1 ),
const,
Здесь
при
на контуре
(1)
x~
(2)
(3)
- граница обтекаемого тела, 0 - случай плоского обтекания, 1 - случай
осесимметричного обтекания, скорость набегающего потока направлена вдоль оси x и равна 1.
3.
Согласно методу ГИУ, решение задачи - функцию токабудем искать в
виде суперпозиции функции тока невозмущенного набегающего потока 0 и
функции тока набора кольцевых вихрей непрерывно распределенных вдоль
обтекаемого тела :
( x, y ) o ( x, y )
где
1 2
( ) M d ,
4 L
1
y
o ( x, y )
1
(4)
,
M o 4 ln RR1 1 , M1 R1[( 2 m) K 2E ], m 4 y / R12
R 2 ( x ) 2 ( y ) 2 , R12 ( x ) 2 ( y ) 2
K, E – полные эллиптические интегралы первого и второго рода с модулем m, точка
( , ) L, ( x, y ) произвольная точка пространства.
4.
Рассмотрим осесимметричный случай 1 . Подставляяосевой плоскости течения к полярным координатам
(4) в (3) , переходя в
( r , ) и полагая уравнение
обтекаемого тела в этой плоскости r g ( ) , имеем соотношение
1
g ( ) sin
( ) A[( 2 m) K 2E ]L[ g ( )]d 0
2 0
2
2
где
L2 [ g ( )] g 2 ( ) g , 2 ( ), A2 g 2 ( ) g 2 ( ) 2 g ( ) g ( ) cos( ),
m 4 g ( ) g ( ) sin sin / A2
(5)
5.
Ядро (5) имеет логарифмическую особенность. Для нахождения можноиспользовать равносильное сингулярное ИУ:
6.
Полученное уравнение может быть решено численно, путёмзамены её разностно-суммирующим аналогом с использованием МДВ.
Для отрезка (0, ) введем сетку
k hk , k 1, 2,......, n,
h
2
j j , j 1, 2,......, n 1,
Полученный аппроксимирующий аналог имеет вид :
Некоторые результаты численного решения полученной СЛАУ,
иллюстрирующие сходимость решения от сетки показаны в таблице.
n=10
n=20
n=40
ρ20-ρ10
ρ40-ρ20
0.6667
0.790981
0.838468
0.124281
0,047487
7. Краевые задачи теории фильтрации со свободной границей
Основным соотношением теории фильтрации является закон фильтрации,Дарси который устанавливает связь между вектором скорости фильтрации и тем
полем давления, которое вызывает фильтрационное движение
k
p ,
где p – давление; μ – гидродинамическая вязкость; k – проницаемость
Закон фильтрации вязкопластической нефти через пористую среду
0, если p o ;
k o
1
p, если
p
p o
где o = * m / k условимся называть начальным градиентом сдвига или
начальным градиентом
8.
Альтернативная модель фильтрации :0, если p o ;
k
p,
если
p o
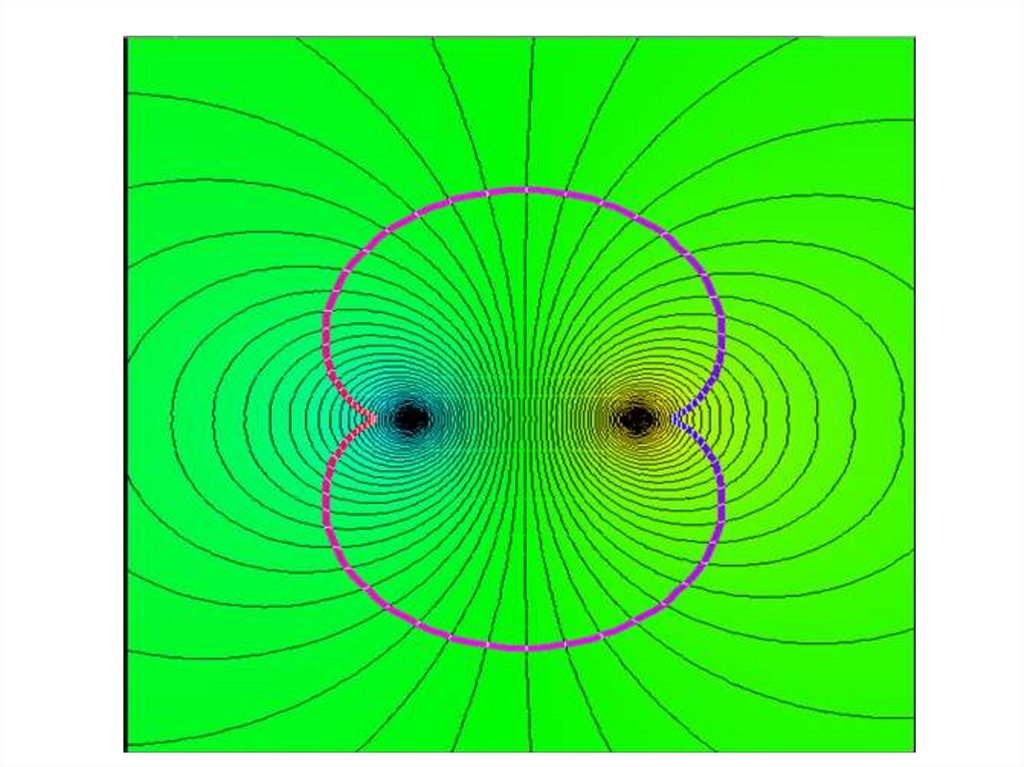
Рассмотрим фильтрационный поток, образуемый диполем с моментом – M,
помещённым в начало координат. В силу малости градиентов давления
образуется застойная зона ABC с неизвестной границей, вдоль которой модуль
скорости равен минимальной скорости vo
k
G . Т.о. зона течения будет иметь
вид, изображённый на рис. , если ограничиться рассмотрением течения при
Im z 0 .
9.
Параметрическое решение задачи, полученное методами ТФКП1 1 1 1 1 2 2
1 2 4
x( )
ln
1 2 1 (1 2 ) (1 2 )(1 2 2 )
y( )
1 1 1
( 1)
arctg
1 1
1 2 1 2 2 1 2
При этом численное значение параметра , используемое в системе, может
быть найдено из уравнения
avo
( 1) 2 ( 1) 2
2
ln
1
,
, 1 ,
4
Q
( 1) 2
10. Соответствующая краевая задача
p 0 в области(1)
p
d j Q j , i 1, 2
j 0 j n
k
(2)
lim
p
0,
n
Здесь
на контуре
(3)
p
G, на контуре
s
(4)
- граница застойной области, j - контур, охватывающий j-тую скважину с дебитом
Q j , расположенную в точке ( x j , y j ); n, s – внутренняя нормаль и касательная к контуру ; к
- заданная постоянная проницаемости среды. Индексом плюс отмечено предельное значение
нормальной производной давления при приближении к границе
изнутри.
11.
Согласно методу ГИУ, решение задачи - функцию распределениядавления будем искать в виде суперпозиции потенциала внешнего поля po ( x, y)
и потенциала простого слоя с неизвестной плотностью , сосредоточенной на
контуре :
p ( x, y ) p o ( x, y )
( , ) ln
2
где
po ( x, y )
i 1
1
(x ) ( y )
2
2
d ,
Qi
ln ( x xi ) 2 ( y yi ) 2 ,
2 k
Здесь ( , ) – точка, принадлежащая контуру ; (x, y) – произвольная точка в пространстве
.
R2
12.
Пусть контур границы застойной области ∂Ω = {r =g (θ), где 0≤ θ ≤ 2π}задан в полярных координатах. Подставляя выражение для функции давления
p(x,y) в граничные условия и учитывая, что нормальная производная потенциала
простого слоя терпит разрыв первого рода в точках контура ∂Ω со скачком 2πρ,
получим систему двух интегральных уравнений
po ( x, y)
1
( , ) ln
( x, y) 0
2
2
n
n
(x ) ( y )
po ( x, y)
1
( , ) ln
G
2
2
s
s
(x ) ( y )
(5)
(6)
13.
Переходя в полученных уравнениях к полярным координатам и используя затемформулы для нахождения частных производных по направлению нормали и касательной,
будем иметь систему двух интегродифференциальных уравнений для отыскания двух
неизвестных функций: плотности ρ(θ), сосредоточенной на контуре ∂Ω и формы самого
контура g(θ), где 0≤ θ ≤ 2π
( )
( ) N , , g ( ), g ( )
Q
2
2
g
(
)
g
(
)
d
0 g 2 ( ) g 2 ( )
2 k
2
N 0, , a, g ( ) N , , a, g ( )
1
g 2 ( ) g 2 ( )
(7)
0
Q
1
( ) K , , g ( ), g ( )
K 0, , a, g ( ) K , , a, g ( )
2 k
g 2 ( ) g 2 ( ) 0
g 2 ( ) g 2 ( )
(8)
2
g 2 ( ) g 2 ( ) G
g 2 ( ) g ( ) g ( ) cos( ) g ( ) g ( ) sin( )
Здесь N , , g ( ), g ( )
g 2 ( ) 2 g ( ) g ( ) cos( ) g 2 ( )
и
K , , g ( ), g ( )
( g ( ) cos( ) g ( )) g ( ) g ( ) g ( ) sin( )
g 2 ( ) 2 g ( ) g ( ) cos( ) g 2 ( )
14.
Перейдем теперь в уравнениях (7) и (8) к безразмерным величинам,полагая
( )
( )
G
, g ( )
G
aG
Q
g ( ) ,
, D
Da
D
В результате преобразований получим интегральные уравнения такого же вида
с заменой ρ(θ) на (θ), g(θ) на g ( ), a 2 на ε , G и aD, равными единице.
Одновременно введя замену для плотностей
~( ) ( ) g 2 ( ) g 2 ( ) ,
будем иметь систему уравнений (7) и (8) в окончательном виде:
2
1
~ ( ) ~ ( ) N , , g ( ), g ( ) d
N 0, , , g ( )
2
0
(9)
N , , , g ( ) 0
1
2
K (0, ,
2
, g ( )) K ( , , , g ( )) ~( ) K ( , , g ( ), g ( )) d
g 2 ( ) g 2 ( )
0
(10)
15.
Пусть точки t1 0, t 2 , , t n , t n 1 2 разбивают отрезок [0, 2π] на nравных частей длины h=2π/n, а точка t oj является серединой отрезка [ t oj , t oj 1 ] ,
j=1,…, n. Будем говорить, что точки множеств Eo t oj , j 1, 2, , n образуют
каноническое разбиение отрезка [0, 2π] с шагом h. Тогда вместо системы (9)(10) будем исследовать следующий аппроксимирующий аналог
n
1
~
j h ~ k N g k , g j
N , j , , g j
2
k 1
N 0, j , , g j
1
2
K 0, ,
, g j K , , , g j h ~ k K g k , g j
n
k 1
g 2 j g 2 j ,
где точки
(11)
j и j принадлежат множеству E0 , n – нечётное число.
(12)
16.
Пользуясь симметрией контура и плотностей, сосредоточенных на этомконтуре,
систему
нелинейных
уравнений,
справедливую
для
отрезка
интегрирования [0, 2π], можно переписать для отрезка [0, π]. Действительно,
т.к. ρ(α)=ρ(-α) и g(α)=g(-α), 0≤ α ≤π, то система (11) - (12) на отрезке [0, π]
примет следующий вид
m
~ j h ~ k N k , j , g k , g j N k , j , g k , g j
k 1
1
2
1
2
N , ,
K 0,
j
j
, g j N 0, j , , g j ,
где
j 1, 2, , m ,
m
, , g j K , j , , g j h ~ k K k , j , g k , g j
K k , j , g k , g j g 2 j g 2 j ,
m n 2 , n-нечётное число.
(13)
k 1
j 1, 2, , m
(14)
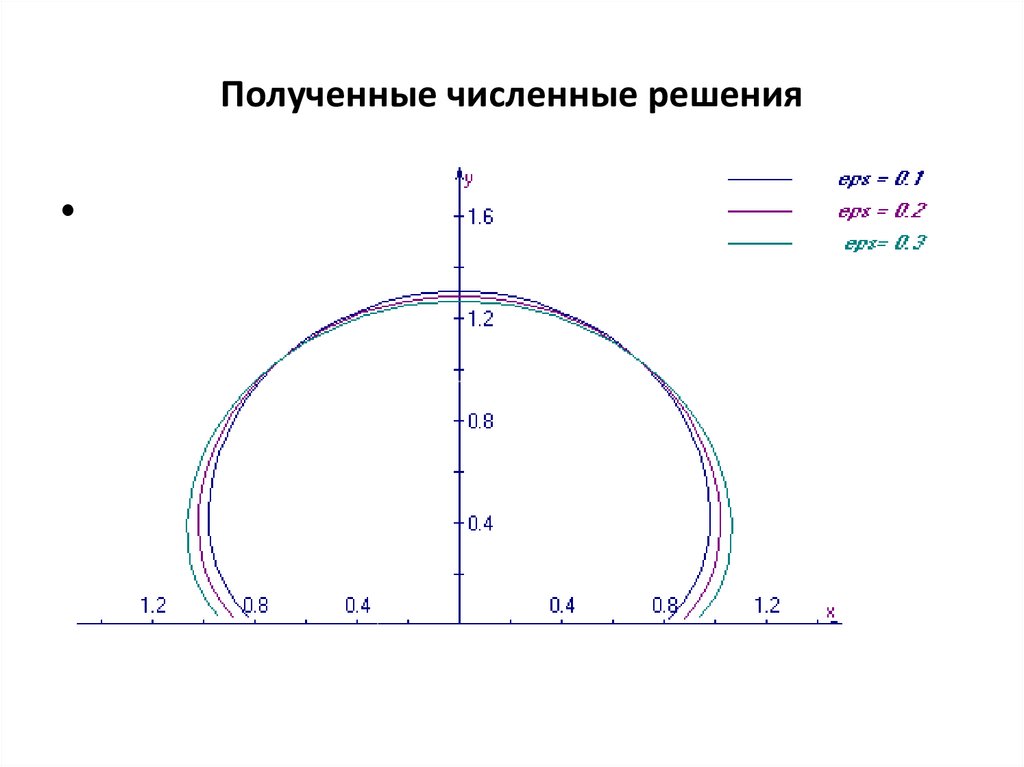
17. Полученные численные решения
18.
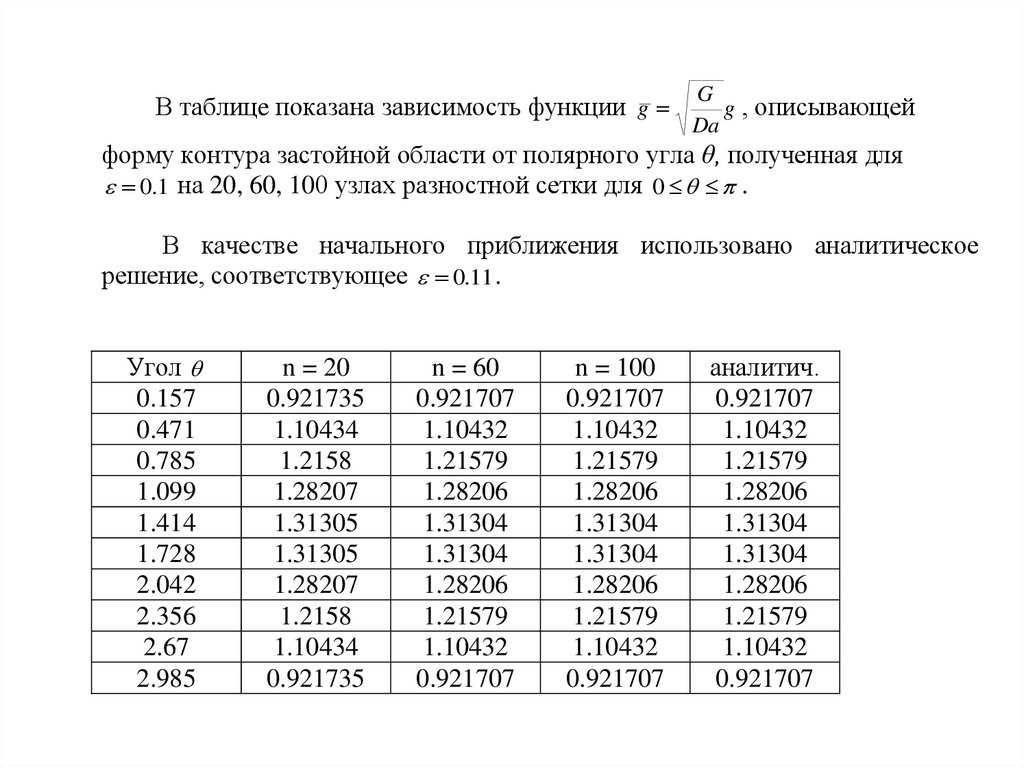
В таблицe показана зависимость функции gG
g , описывающей
Da
форму контура застойной области от полярного угла θ, полученная для
0.1 на 20, 60, 100 узлах разностной сетки для 0 .
В качестве начального приближения использовано аналитическое
решение, соответствующее 0.11 .
Угол
0.157
0.471
0.785
1.099
1.414
1.728
2.042
2.356
2.67
2.985
n = 20
0.921735
1.10434
1.2158
1.28207
1.31305
1.31305
1.28207
1.2158
1.10434
0.921735
n = 60
0.921707
1.10432
1.21579
1.28206
1.31304
1.31304
1.28206
1.21579
1.10432
0.921707
n = 100
0.921707
1.10432
1.21579
1.28206
1.31304
1.31304
1.28206
1.21579
1.10432
0.921707
аналитич.
0.921707
1.10432
1.21579
1.28206
1.31304
1.31304
1.28206
1.21579
1.10432
0.921707
19.
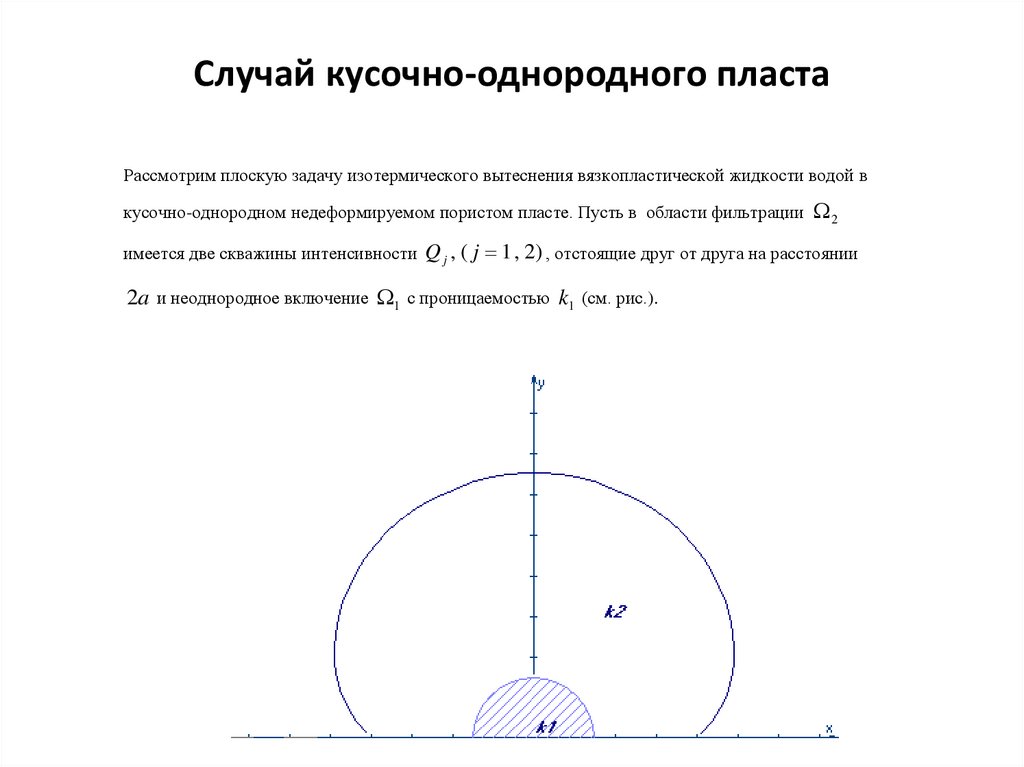
20. Случай кусочно-однородного пласта
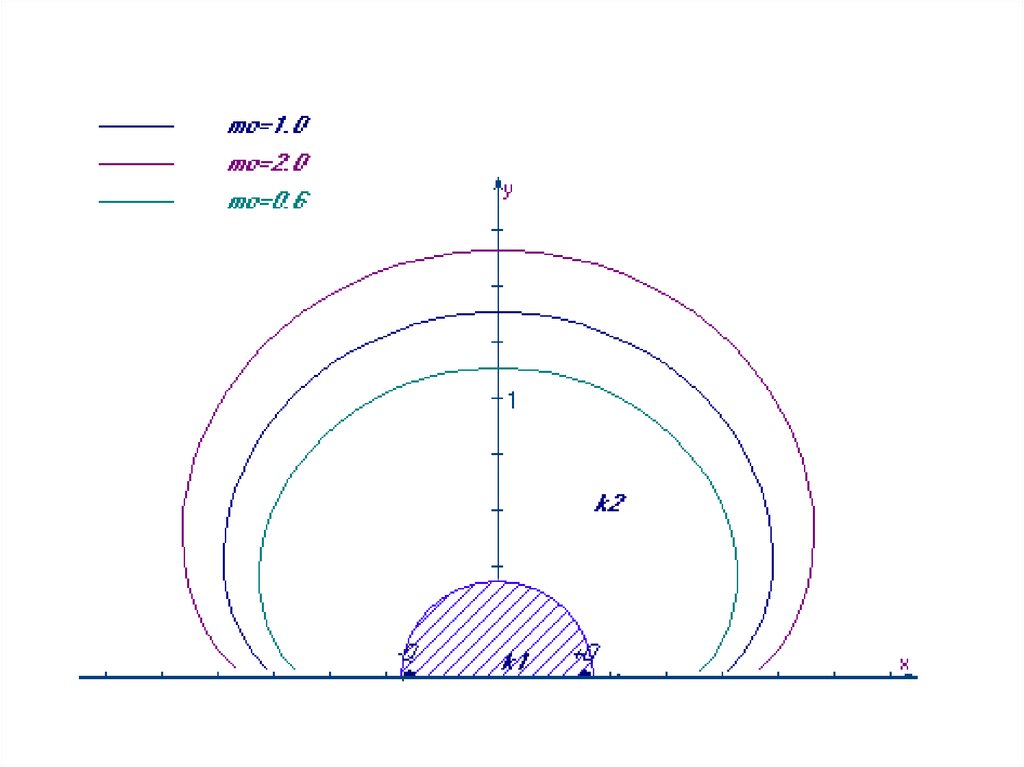
Рассмотрим плоскую задачу изотермического вытеснения вязкопластической жидкости водой вкусочно-однородном недеформируемом пористом пласте. Пусть в области фильтрации
2
имеется две скважины интенсивности Q j , ( j 1 , 2) , отстоящие друг от друга на расстоянии
2a и неоднородное включение 1 с проницаемостью k1 (см. рис.).
21.
p 0 в области 2(15)
p
d j Q j ,
j 0 j n j
k
lim
p
0,
n2
p
G
s
j 1, 2
(16)
на контуре 2
(17)
p ( x, y )
p ( x, y )
p p , k1
k 2
на контуре 1
n
n
1
1
Здесь
(18)
1 - замкнутый контур скачка проницаемости, j - контур, охватывающий j-тую
скважину с дебитом Q j , расположенную в точке x j , y j
j 1, 2 , n (n
i
j
), s i
внутренняя нормаль и касательная к контуру i ( j ), k1 , k 2 заданные постоянные
проницаемости областей
2 \ 1 и 2 соответственно.
22.
22 1 N g1 , g 2
0
g 22 g 22
g g 2
2
2
2
g12 g1 2
g 22 g 22
2
d 2 N g 2 , g 2
0
Q
N 0, , a, g 2 ( ) N , , a, g 2 ( ) 2 1 2 0
2 k
g 2 ( ) g 2 ( )
d
2
Q
K 0, , a, g 2 ( ) K , , a, g 2 ( ) 2 1 2 1 K g1 , g 2
2 ki
g 2 g 2 0
g12 g1 2
g 22 g 2 2
2
d 2 K g 2 , g 2
2 ki
2
1 N g1 , g 2
0
g 22 g 2 2
0
k1 k 2 1 ( ) k 2 k1 Q
g 22 g 22
g 22 g 22
0
d
2
2
g1 g1
1
g12 ( ) g1 2 ( )
g12 g12
g12 g1 2
d G
N 0, , a, g1 ( ) N , , a, g1 ( )
2
d 2 N g 2 , g 2
0



















 Математика
Математика Физика
Физика








