Похожие презентации:
Построение регрессионной модели
1. Построение регрессионной модели
2.
Ms Excel – это универсальнаясистема обработки данных,
которая может
использоваться для анализа
и представления данных в
наглядной форме.
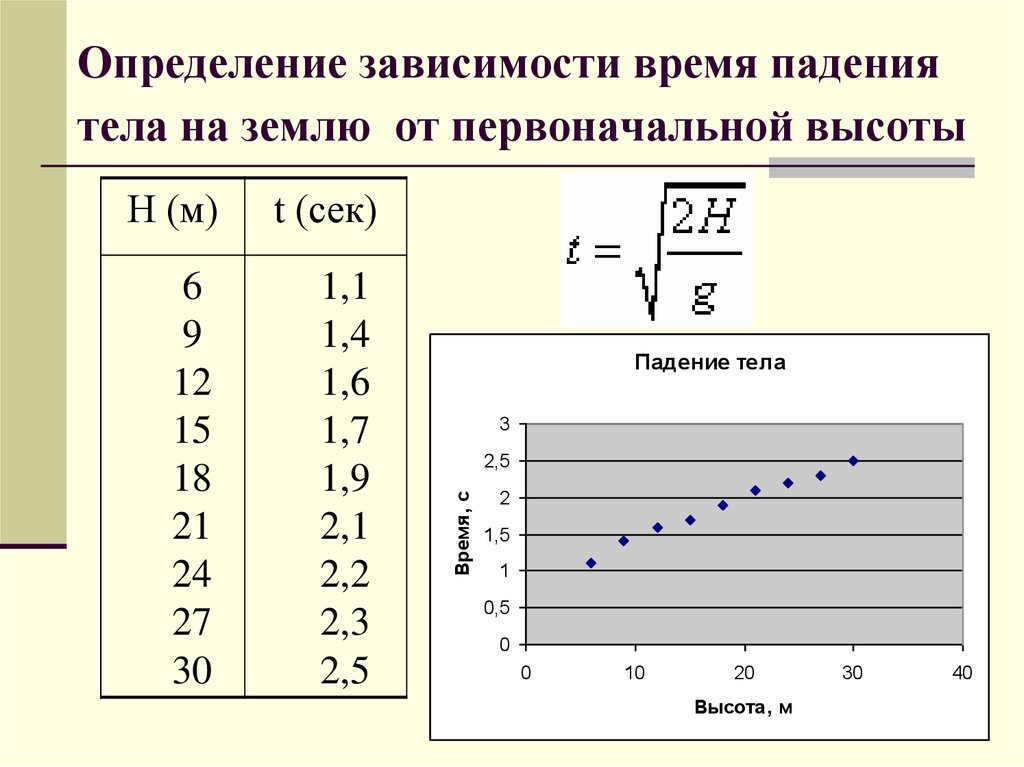
3. Определение зависимости время падения тела на землю от первоначальной высоты
t (сек)6
9
12
15
18
21
24
27
30
1,1
1,4
1,6
1,7
1,9
2,1
2,2
2,3
2,5
Падение тела
3
2,5
Время, с
Н (м)
2
1,5
1
0,5
0
0
10
20
Высота, м
30
40
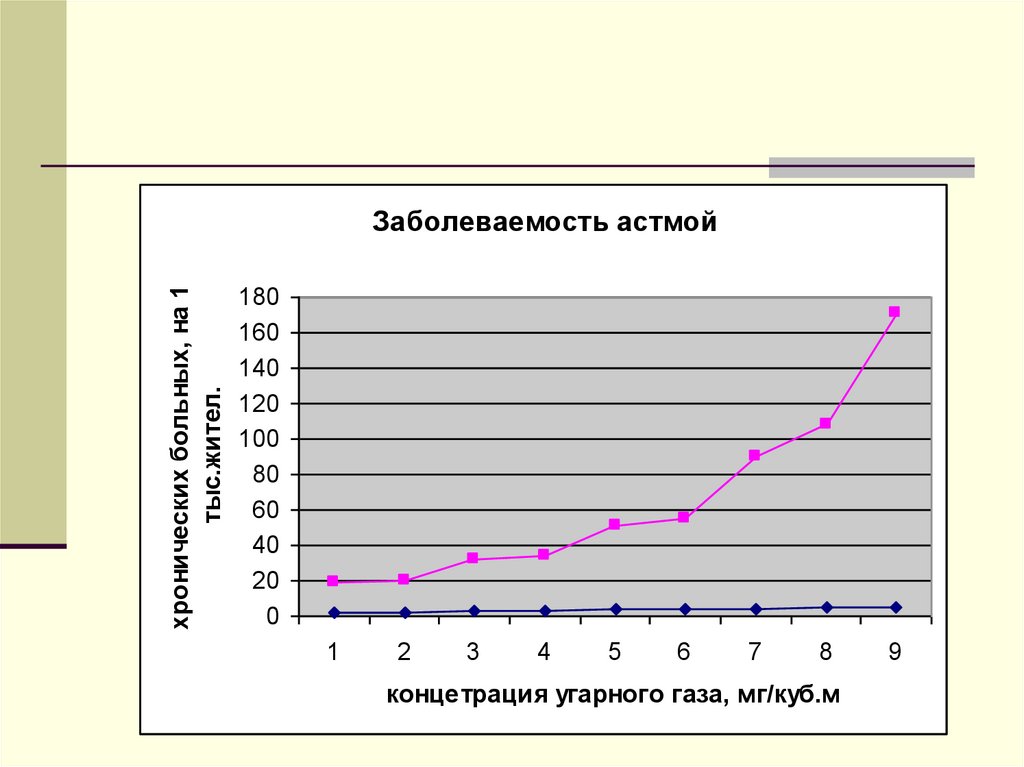
4. КАК найти зависимость частоты заболеваемости жителей города бронхиальной астмой от качества воздуха?
5. Статистика – наука о сборе, изменении и анализе массовых количественных данных.
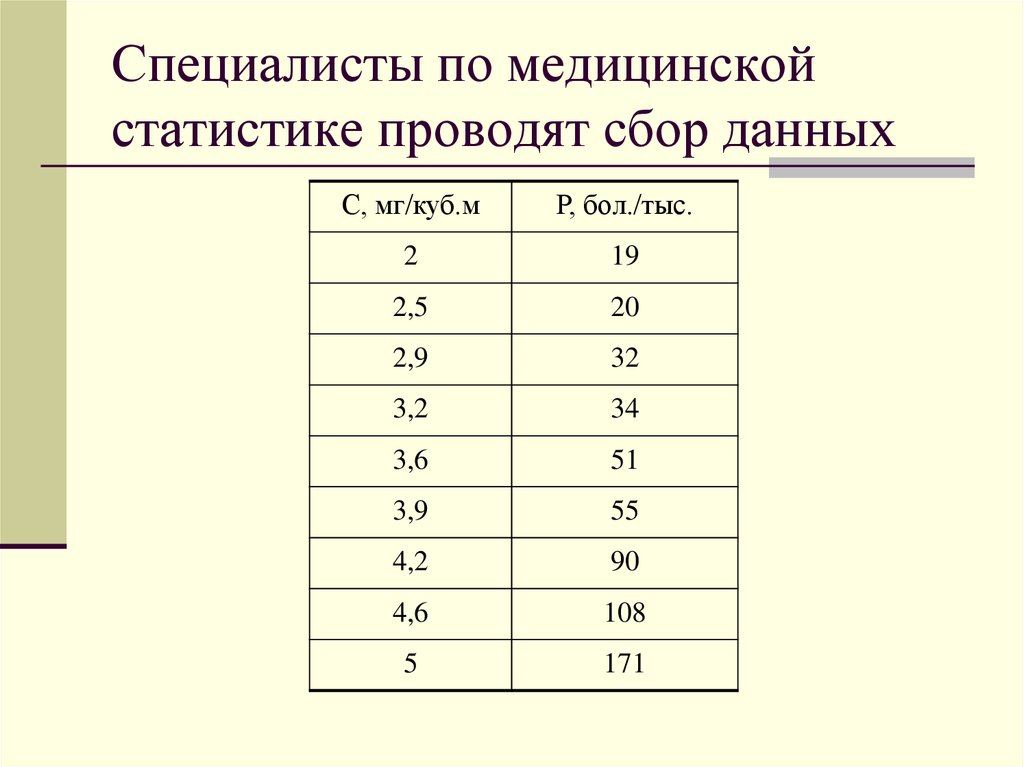
6. Специалисты по медицинской статистике проводят сбор данных
С, мг/куб.мР, бол./тыс.
2
19
2,5
20
2,9
32
3,2
34
3,6
51
3,9
55
4,2
90
4,6
108
5
171
7.
хронических больных, на 1тыс.жител.
Заболеваемость астмой
180
160
140
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
концетрация угарного газа, мг/куб.м
9
8.
Необходимо получитьформулу, отражающую эту
зависимость.
На языке математики это
называется функцией
зависимости Р от С:
Р(С)
9. Требования к искомой функции
она должна быть достаточно простой дляиспользования её в дальнейших
вычислениях;
график этой функции должен проходить
вблизи экспериментальных точек так,
чтобы отклонения этих точек от графика
были минимальны и равномерны
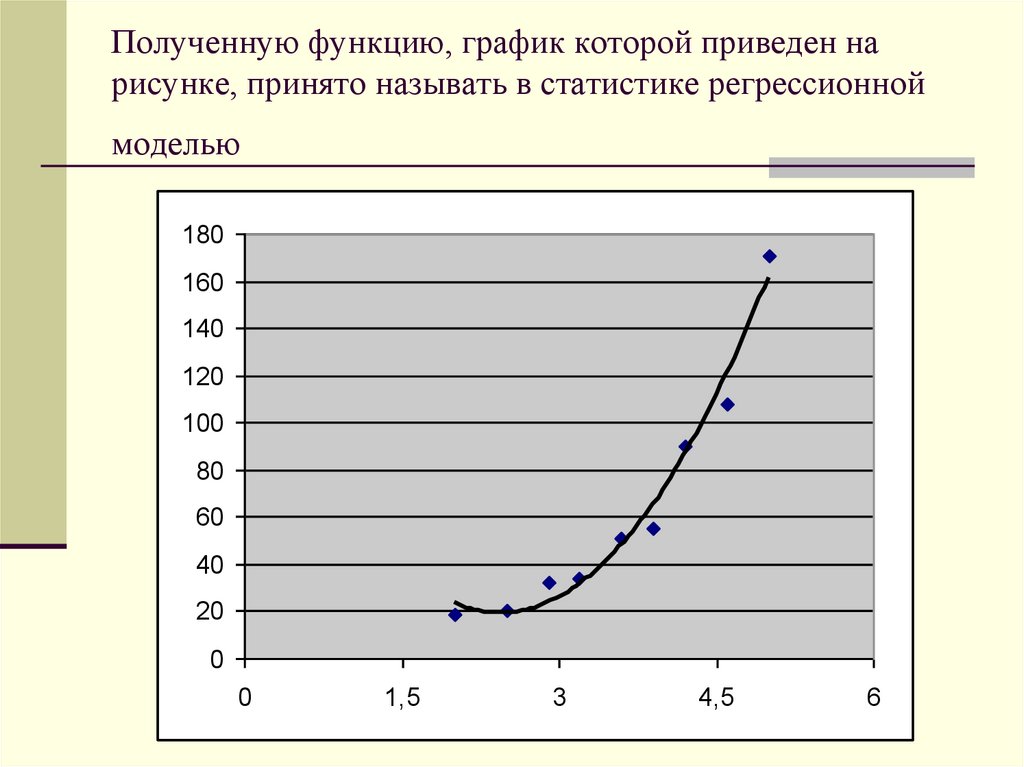
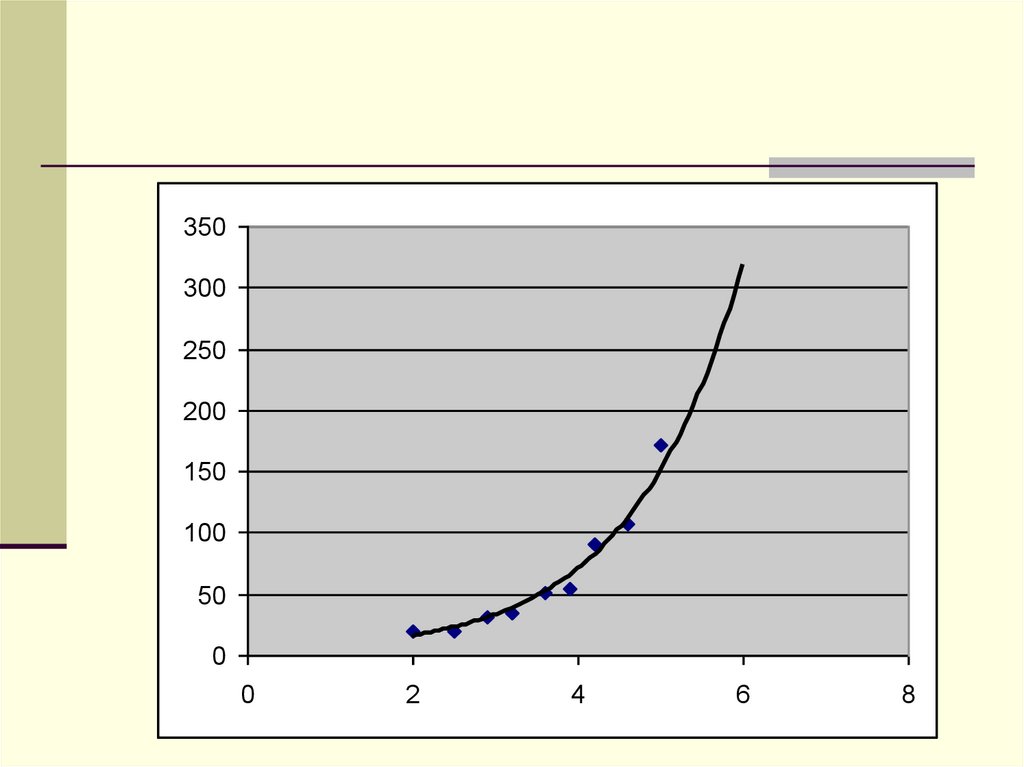
10. Полученную функцию, график которой приведен на рисунке, принято называть в статистике регрессионной моделью
180160
140
120
100
80
60
40
20
0
0
1,5
3
4,5
6
11.
Регрессионная модель –это функция, описывающая
зависимость между
количественными
характеристиками сложных
систем
12. Получение регрессионной модели
подбор вида функции;вычисление параметров
функции.
13. Выбор производится среди следующих функций
y=ax+b – линейная функция;y=ax2+bx+c – квадратичная функция;
y=aln(x)+b – логарифмическая функция;
y=aebx
y=axb
- экспоненциальная функция;
- степенная функция.
14. Метод наименьших квадратов (МНК)
Искомая функция должна бытьпостроена так, чтобы сумма
квадратов отклонений у –
координат всех экспериментальных
точек от у – координат графика
функции была бы минимальной
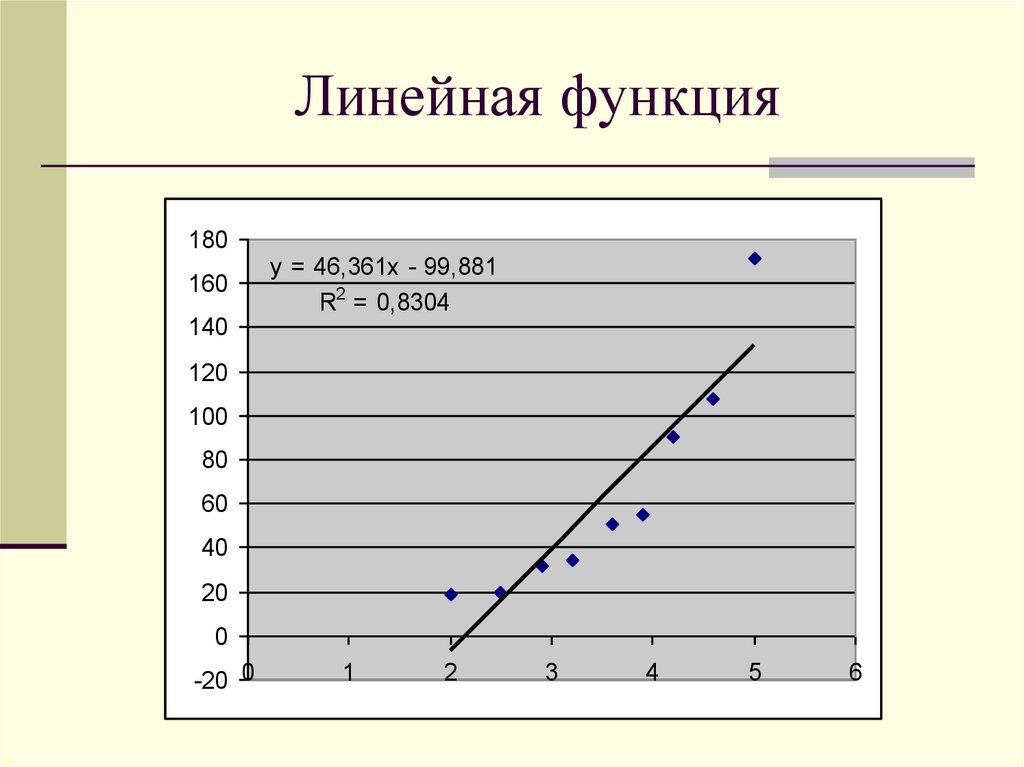
15. Линейная функция
180160
140
y = 46,361x - 99,881
R2 = 0,8304
120
100
80
60
40
20
0
-20 0
1
2
3
4
5
6
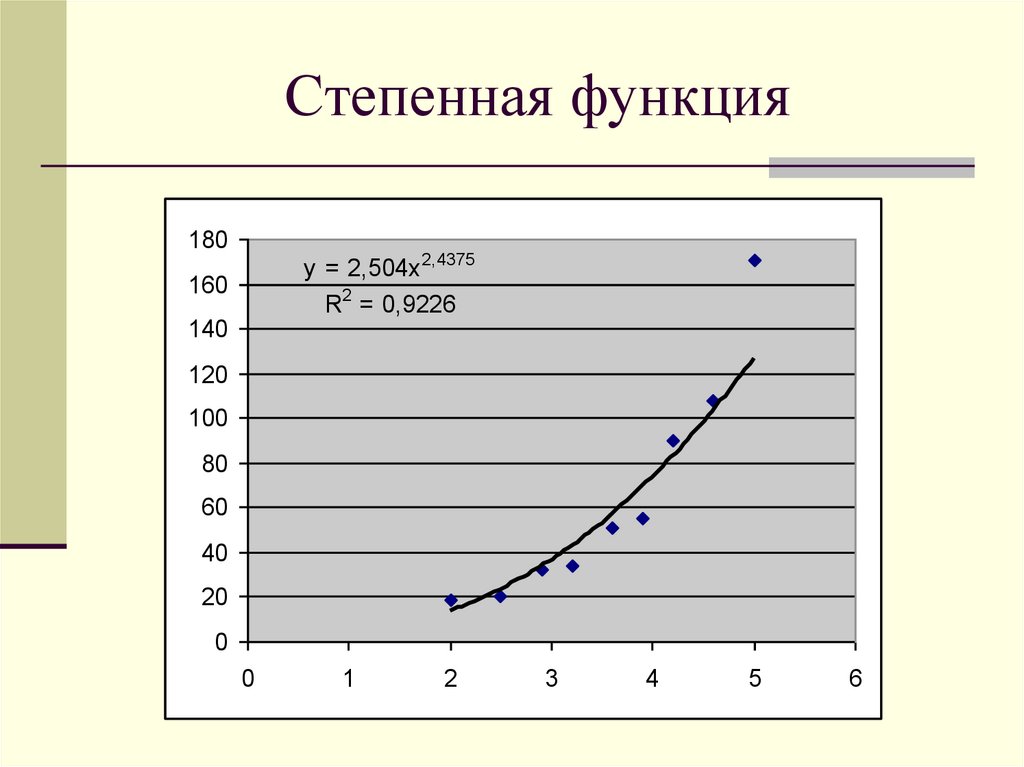
16. Степенная функция
180y = 2,504x 2,4375
R2 = 0,9226
160
140
120
100
80
60
40
20
0
0
1
2
3
4
5
6
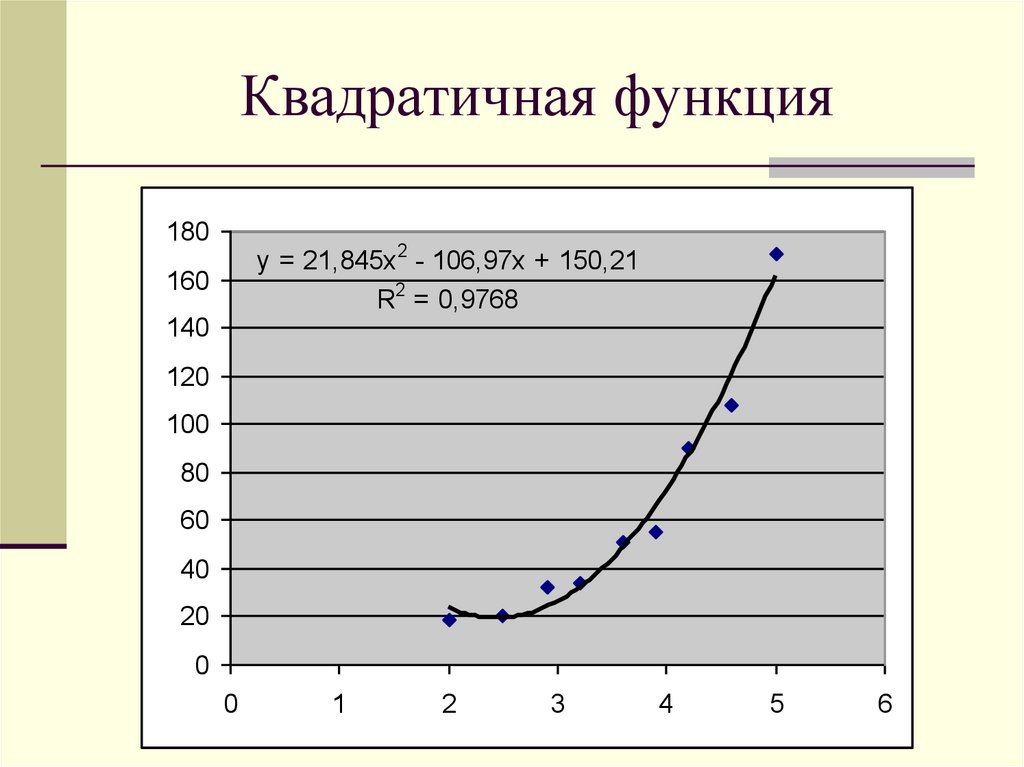
17. Квадратичная функция
180y = 21,845x 2 - 106,97x + 150,21
R2 = 0,9768
160
140
120
100
80
60
40
20
0
0
1
2
3
4
5
6
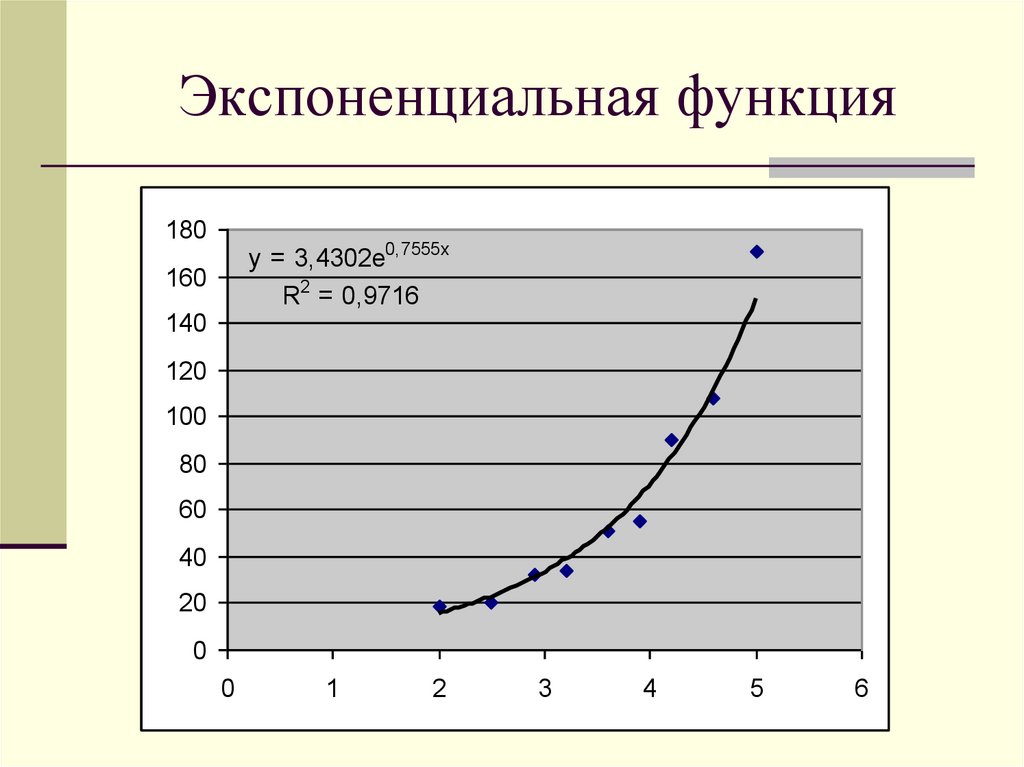
18. Экспоненциальная функция
180y = 3,4302e0,7555x
R2 = 0,9716
160
140
120
100
80
60
40
20
0
0
1
2
3
4
5
6
19. R2 - коэффициентом детерминированности
0<Плохая
модель
2
R
<1
Хорошая
модель
20. Способы прогнозов по регрессионной модели
Восстановление значения - прогнозпроизводится в пределах
экспериментальных значений
независимой переменной
Экстраполяция - прогнозирование
за пределами экспериментальных
данных
21.
350300
250
200
150
100
50
0
0
2
4
6
8