Расстояние между скрещивающимися прямыми

1. Задание 13. Расстояние между скрещивающимися прямыми.

2.

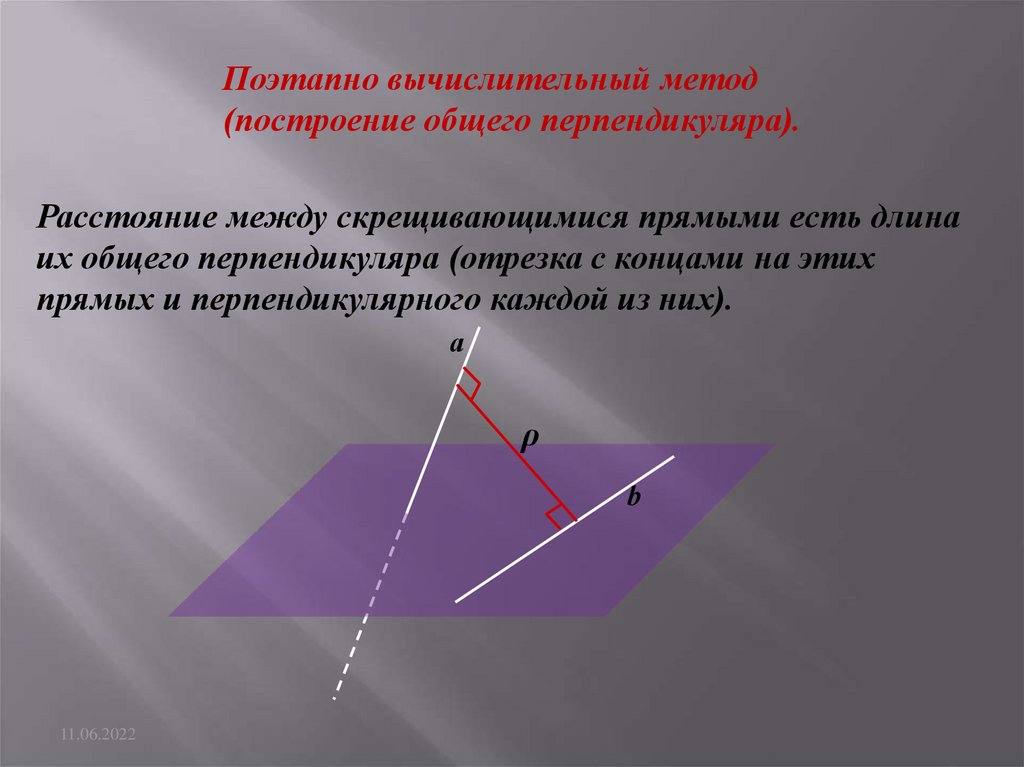
Поэтапно вычислительный метод
(построение общего перпендикуляра).
Расстояние между скрещивающимися прямыми есть длина
их общего перпендикуляра (отрезка с концами на этих
прямых и перпендикулярного каждой из них).
а
ρ
b
11.06.2022

3.

Метод параллельных прямой и плоскости.
Построить плоскость, содержащую
одну из прямых и параллельную
второй. Тогда искомое расстояние
будет равно расстоянию от какойнибудь точки второй прямой до
построенной плоскости (на этом
этапе можно использовать
координатный метод)
α
http://tashah.ucoz.ru/load/egeh/egeh_s2/k
oordinatnyj_metod_kljuchevye_za
dachi/14-1-0-73
11.06.2022
a║
b
AB
А
а
ρ
b
В
( a ; b ) AB
3

4.

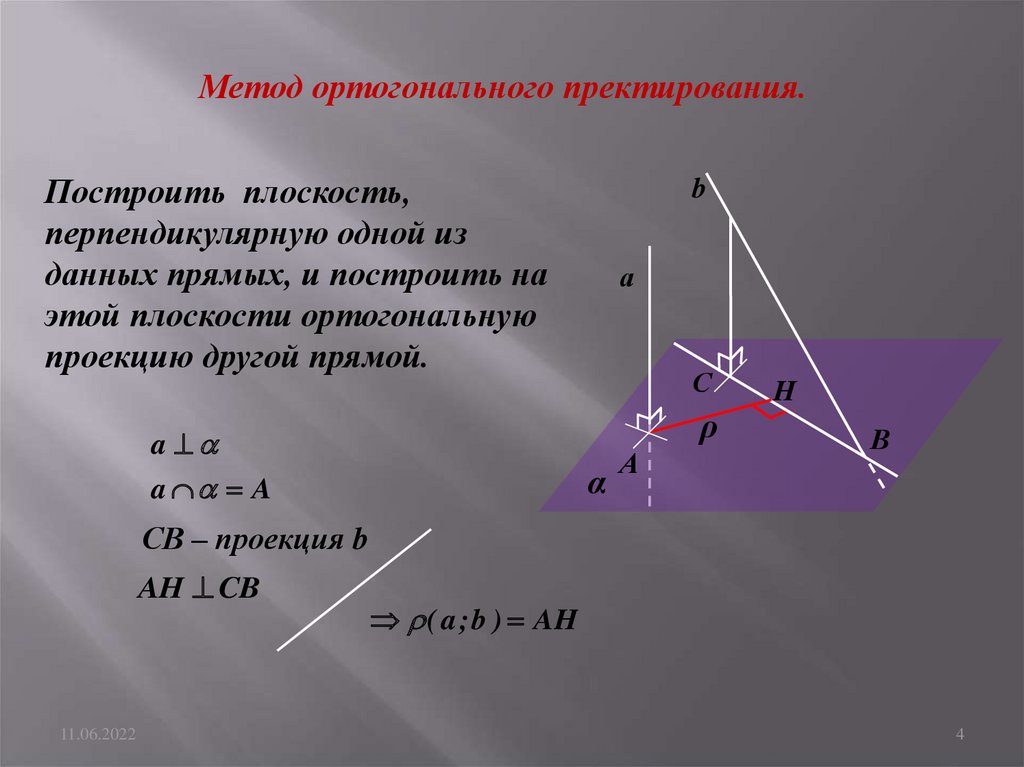
Метод ортогонального пректирования.
Построить плоскость,
перпендикулярную одной из
данных прямых, и построить на
этой плоскости ортогональную
проекцию другой прямой.
b
а
С
ρ
a
α
a A
А
Н
В
СВ – проекция b
AH CB
11.06.2022
( a ; b ) AH
4

5.

Опорная задача.
Если AB и CD –
скрещивающиеся ребра
треугольной пирамиды
ABCD, d – расстояние
между ними, α – угол между
AB и CD, V – объем
пирамиды ABCD, то
D
C
А
6V
d
АВ CD sin
B
Методы нахождения угла между прямыми
смотри по адресу:
Пример
http://ta-shah.ucoz.ru/load/egeh/egeh_s2/s2_4_ugol_mezhdu_prjamymi/14-1-0-78
11.06.2022
5

6.

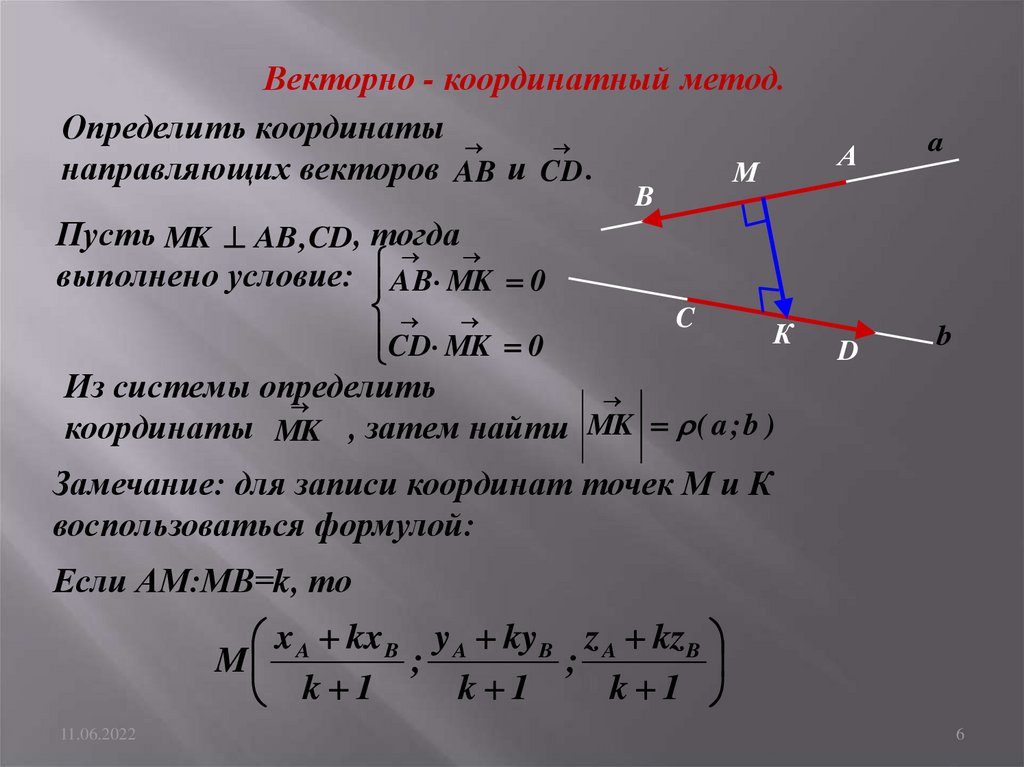
Векторно - координатный метод.
Определить координаты
направляющих векторов AB и CD .
М
А
a
B
Пусть MK AB , CD, тогда
выполнено условие: AB MK 0
CD MK 0
C
К
D
b
Из системы определить
координаты MK , затем найти MK ( a ; b )
Замечание: для записи координат точек М и К
воспользоваться формулой:
Если АМ:МВ=k, то
x A kx B y A kyB z A kz B
M
;
;
k 1
k 1
k 1
11.06.2022
6

7.

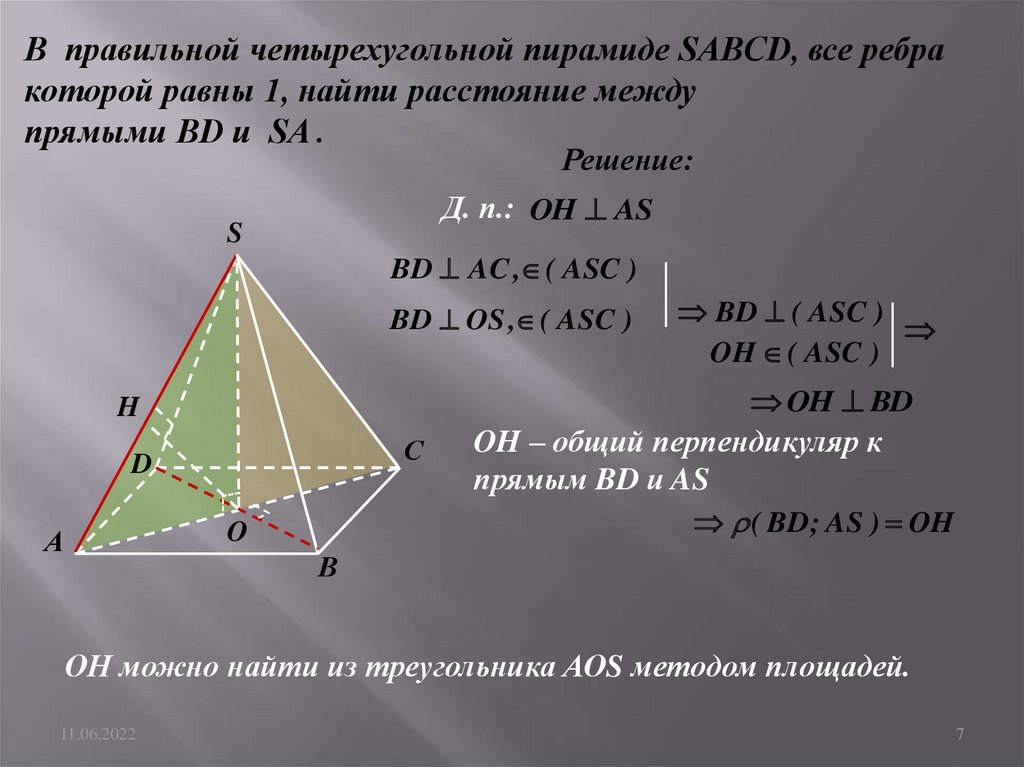
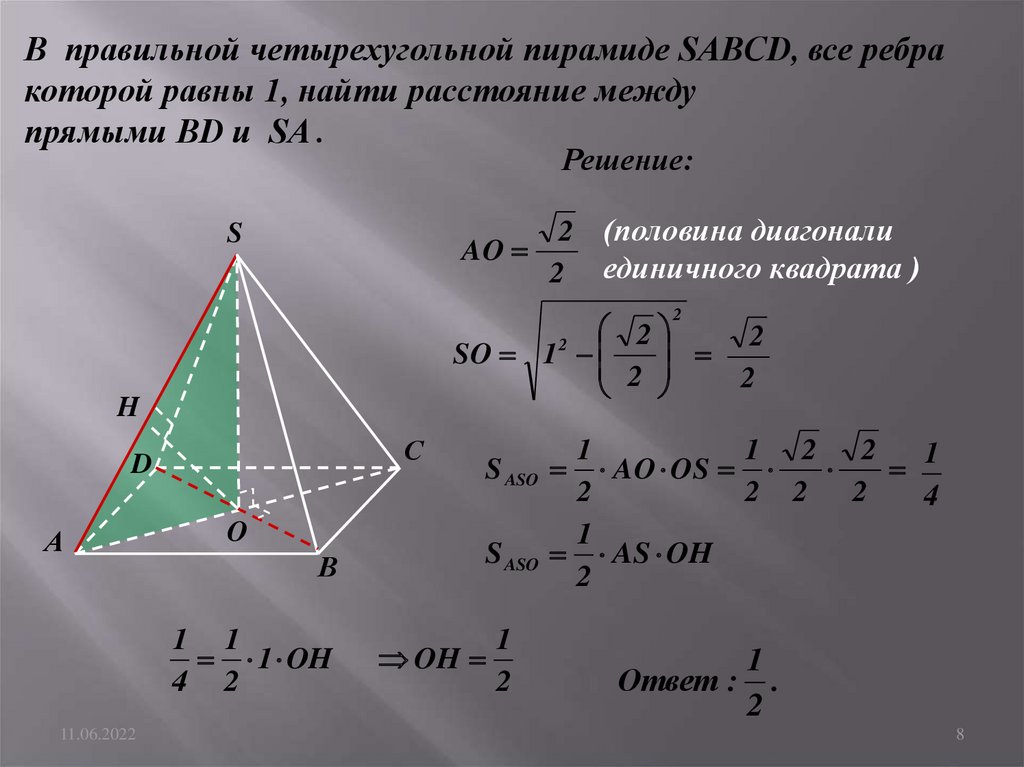
В правильной четырехугольной пирамиде SABCD, все ребра
которой равны 1, найти расстояние между
прямыми BD и SA .
Решение:
Д. п.: OH AS
S
BD AC , ( ASC )
BD OS , ( ASC )
H
С
D
O
А
BD ( ASC )
OH ( ASC )
OH BD
OH – общий перпендикуляр к
прямым BD и AS
( BD ; AS ) OH
В
ОН можно найти из треугольника АОS методом площадей.
11.06.2022
7

8.

В правильной четырехугольной пирамиде SABCD, все ребра
которой равны 1, найти расстояние между
прямыми BD и SA .
Решение:
S
AO
2
2
(половина диагонали
единичного квадрата )
2
2
2
SO 1
2
H
С
D
А
O
В
1 1
1 OH
4 2
11.06.2022
S ASO
S ASO
1
OH
2
2
2
1
1 2
2
1
AO OS
2
2 2
2
4
1
AS OH
2
1
Ответ : .
2
8

9.

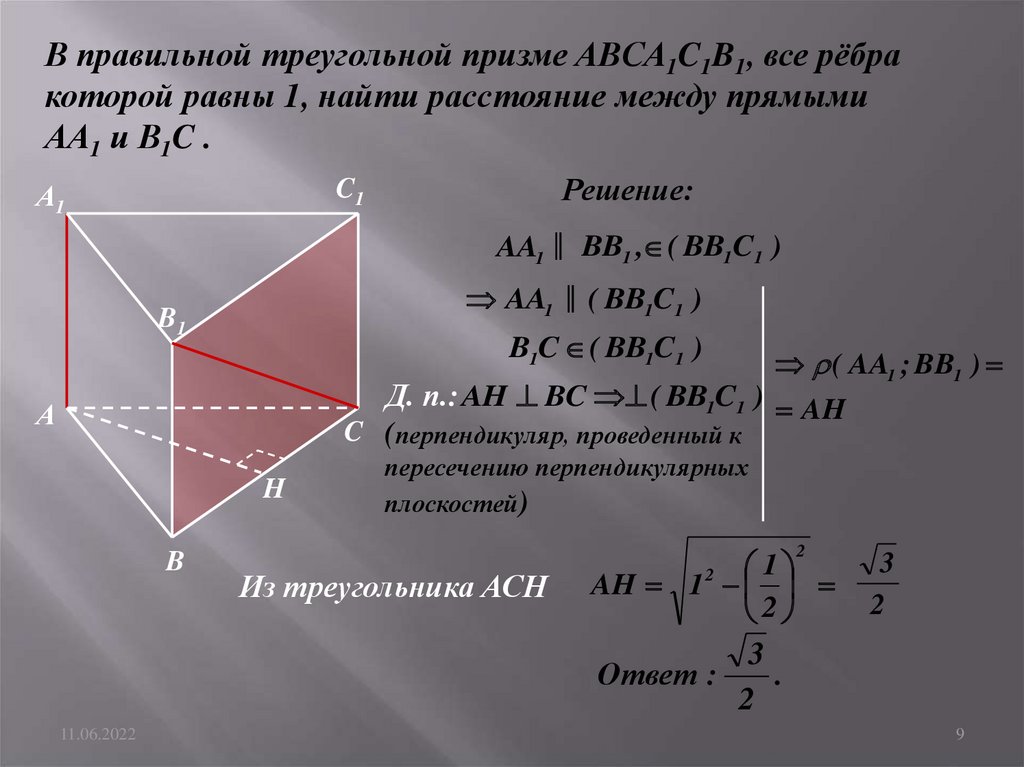
В правильной треугольной призме ABCA1C1B1, все рёбра
которой равны 1, найти расстояние между прямыми
АA1 и B1C .
Решение:
C1
А1
AA1 ║ BB1 , ( BB1C1 )
AA1
B1
║
( BB1C1 )
B1C ( BB1C1 )
( AA1 ; BB1 )
Д. п.: AH BC ( BB1C1 ) AH
C (перпендикуляр, проведенный к
А
H
B
пересечению перпендикулярных
плоскостей)
2
Из треугольника АСН
1
2
AH 1
2
3
2
3
Ответ :
.
2
11.06.2022
9

10.

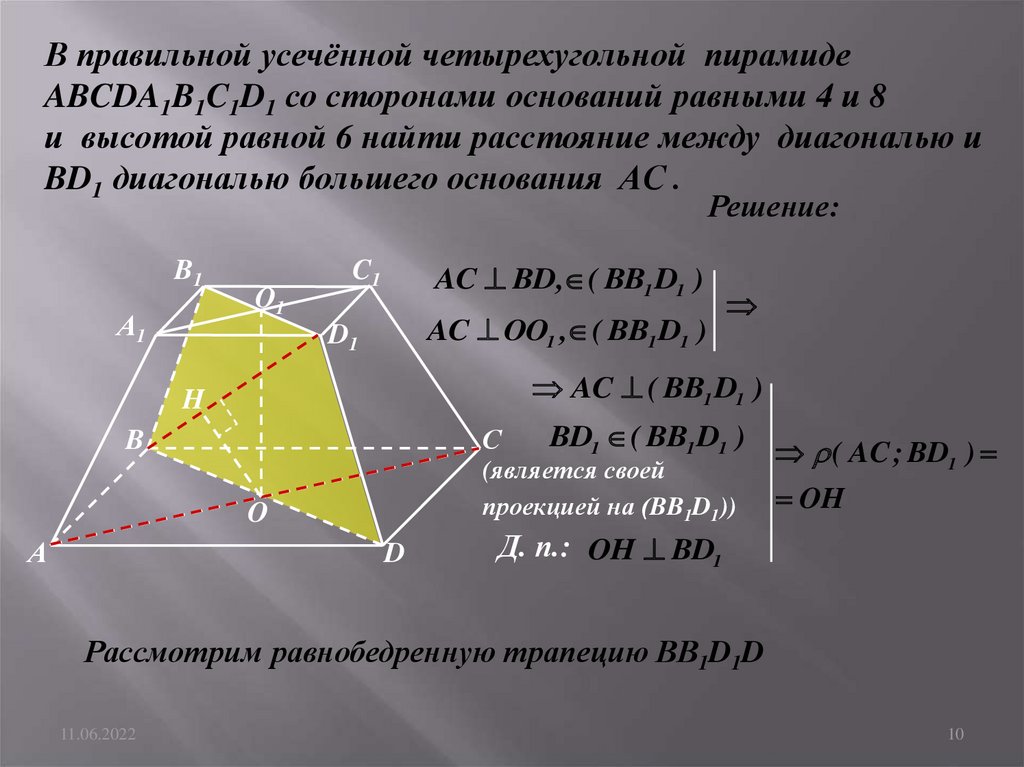
В правильной усечённой четырехугольной пирамиде
ABCDA1B1C1D1 со сторонами оснований равными 4 и 8
и высотой равной 6 найти расстояние между диагональю и
BD1 диагональю большего основания AC .
Решение:
B1
А1
O1
AC BD, ( BB1 D1 )
C1
AC OO1 , ( BB1 D1 )
D1
AC ( BB1 D1 )
H
С
B
BD1 ( BB1 D1 )
(является своей
проекцией на (BB1D1))
O
А
D
( AC ; BD1 )
OH
Д. п.: OH BD1
Рассмотрим равнобедренную трапецию ВВ1D1D
11.06.2022
10

11.

В правильной усечённой четырехугольной пирамиде
ABCDA1B1C1D1 со сторонами оснований равными 4 и 8
и высотой равной 6 найти расстояние между диагональю и
BD1 диагональю большего основания AC .
Решение:
4
B1
D1
Треугольники BD1K и ВОН подобны
по двум углам
В треугольнике ВD1K
H
BK 6
6
В треугольнике ВHO
?
B
O
K
D
8
BD1 D1 K
BO
OH
OH
Ответ : 2 2 .
11.06.2022
BD1 6 2 6 2 6 2
BO 4
6 2
6
4
OH
24
4
2 2
6 2
2
11

12.

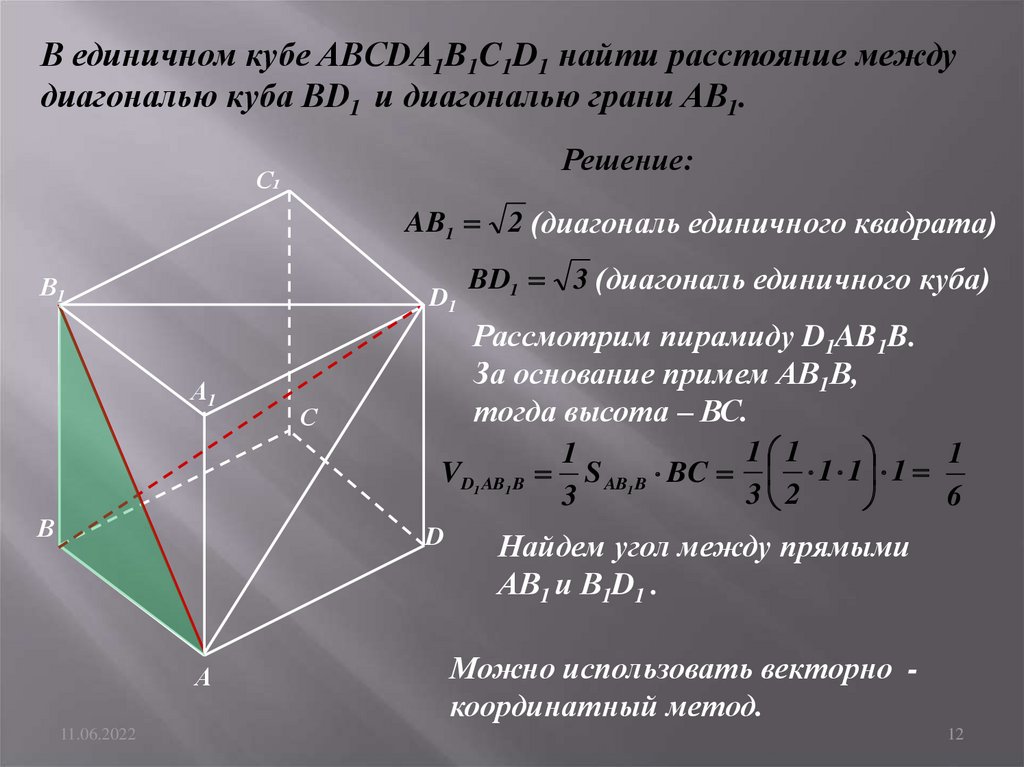
В единичном кубе ABCDA1B1C1D1 найти расстояние между
диагональю куба BD1 и диагональю грани AB1.
Решение:
С₁
AB1 2 (диагональ единичного квадрата)
В1
D1
А1
С
BD1 3 (диагональ единичного куба)
Рассмотрим пирамиду D1AB1B.
За основание примем АВ1В,
тогда высота – ВС.
1 1
1
1
VD AB B S AB B BC 1 1 1
3 2
3
6
1
В
D
А
11.06.2022
1
1
Найдем угол между прямыми
АВ1 и В1D1 .
Можно использовать векторно координатный метод.
12

13.

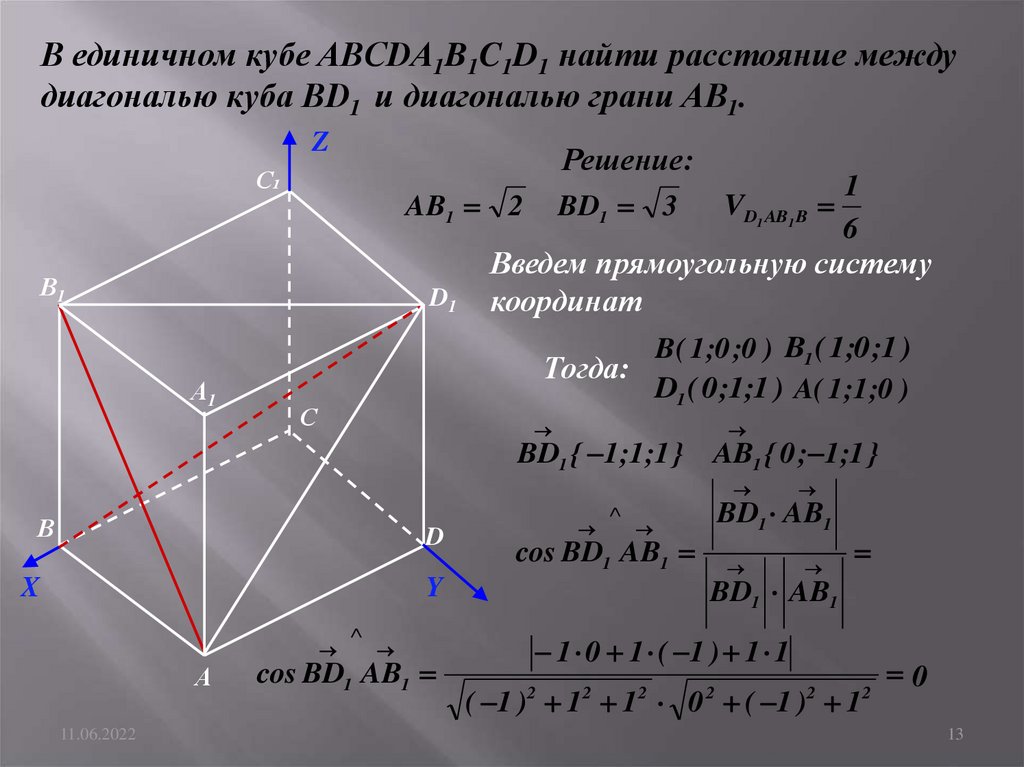
В единичном кубе ABCDA1B1C1D1 найти расстояние между
диагональю куба BD1 и диагональю грани AB1.
Z
Решение:
С₁
1
AB1 2 BD1 3
6
Введем прямоугольную систему
D1 координат
VD1 AB1 B
В1
А1
B( 1 ;0 ;0 ) B1 ( 1;0 ;1 )
Тогда:
D1 ( 0 ;1;1 ) A( 1 ;1 ;0 )
С
BD1 { 1;1;1 } AB1 { 0 ; 1;1 }
В
D
X
Y
А
11.06.2022
cos BD1 AB1
BD1 AB1
cos BD1 AB1
BD1 AB1
1 0 1 ( 1 ) 1 1
( 1 ) 1 1 0 ( 1 ) 1
2
2
2
2
2
2
0
13

14.

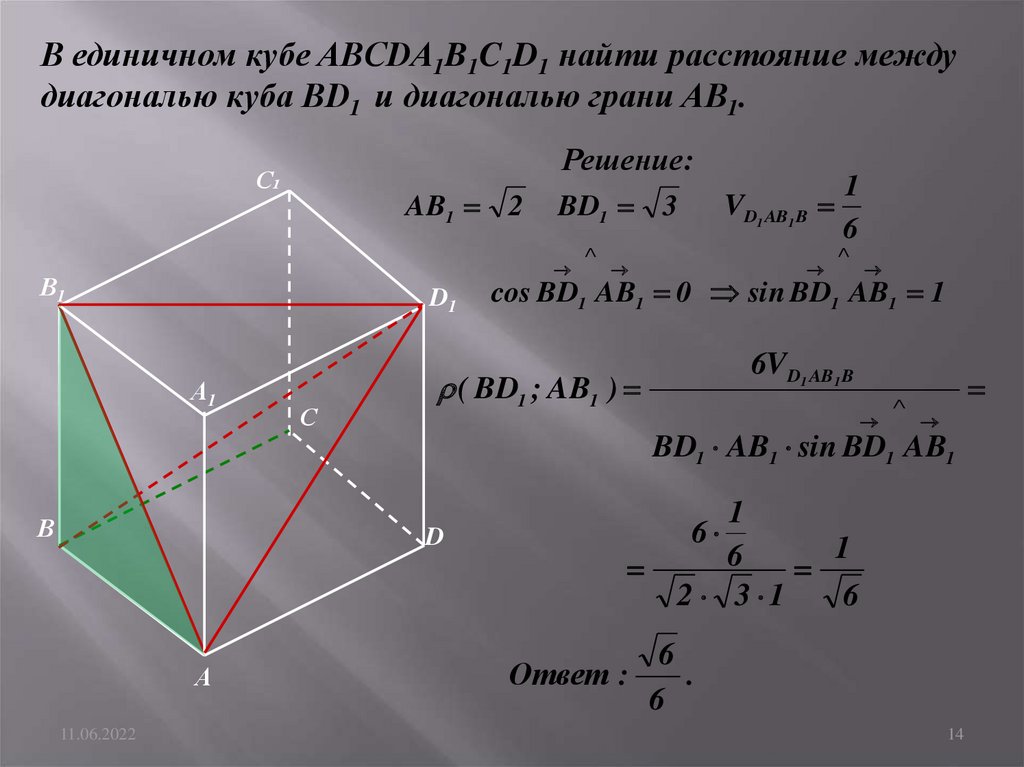
В единичном кубе ABCDA1B1C1D1 найти расстояние между
диагональю куба BD1 и диагональю грани AB1.
Решение:
С₁
AB1 2
В1
D1
А1
В
С
А
1
6
cos BD1 AB1 0 sin BD1 AB1 1
6VD1 AB1 B
( BD1 ; AB1 )
BD1 AB1 sin BD1 AB1
D
11.06.2022
BD1 3
VD1 AB1 B
1
6
1
6
2 3 1
6
6
Ответ :
.
6
14

15.

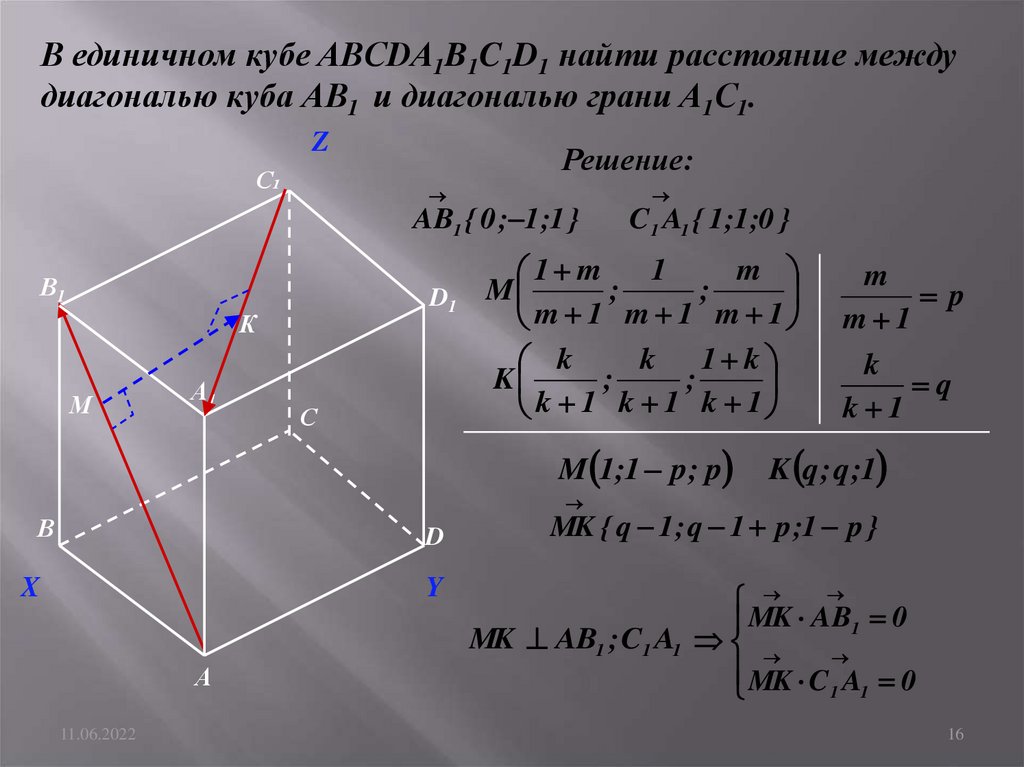
В единичном кубе ABCDA1B1C1D1 найти расстояние между
диагональю куба АВ1 и диагональю грани A1С1.
Z
С₁
Решение:
Введем прямоугольную систему координат
Тогда: B1 ( 1;0 ;1 ) A( 1 ;1 ;0 )
D1
A1 ( 1;1;1 ) C1 ( 0 ;0 ;1 )
В1
К
М
А1
С
В
X
xC1 kx A1
k 1
А K
11.06.2022
AB1 { 0 ; 1;1 } C 1 A1 { 1;1;0 }
AM : MB m
Пусть MK AB1 ; C1 A1 и
C 1 K : KA1 k
Тогда: x mx
y A my B1 z A mz B1
A
B1
M
;
;
m 1
m 1
D
m 1
1
m
1 m
Y
;
;
m 1 m 1 m 1
yC1 ky A1 zC1 kz A1 k
k 1 k
;
;
;
;
k 1
k 1 k 1 k 1 k 1
15

16.

В единичном кубе ABCDA1B1C1D1 найти расстояние между
диагональю куба АВ1 и диагональю грани A1С1.
Z
С₁
Решение:
AB1 { 0 ; 1;1 }
В1
D1
К
М
А1
С
C 1 A1 { 1;1;0 }
1
m
1 m
M
;
;
m
1
m
1
m
1
k 1 k
k
K
;
;
k 1 k 1 k 1
M 1;1 p; p
m
p
m 1
k
q
k 1
K q ; q ;1
В
D
X
Y
А
11.06.2022
MK { q 1; q 1 p ;1 p }
MK AB1 0
MK AB1 ; C1 A1
MK C A 0
1 1
16

17.

В единичном кубе ABCDA1B1C1D1 найти расстояние между
диагональю куба АВ1 и диагональю грани A1С1.
Решение:
AB1 { 0 ; 1;1 } C 1 A1 { 1;1;0 }
MK AB1 0
MK { q 1; q 1 p ;1 p }
MK C A 0
1 1
( q 1 ) 0 ( q 1 p ) ( 1 ) ( 1 p ) 1 0
( q 1 ) 1 ( q 1 p ) 1 ( 1 p ) 0 0
2
p
q 1 p 1 p 0
3
q 1 q 1 p 0
q 2
3
1 1 1
MK ; ;
3 3 3
2
2
1 1 1
MK
3 3 3
11.06.2022
2
3
Ответ :
.
3
17

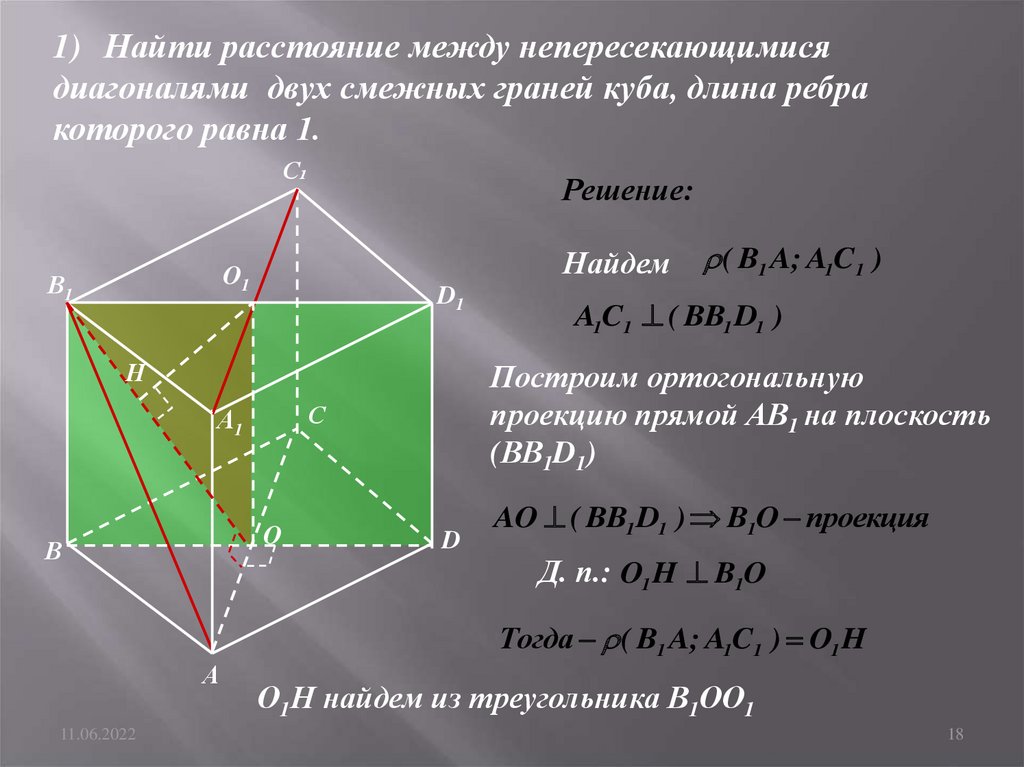
18.

1) Найти расстояние между непересекающимися
диагоналями двух смежных граней куба, длина ребра
которого равна 1.
С₁
Решение:
Найдем
O1
В1
D1
Н
O
В
A1C1 ( BB1 D1 )
Построим ортогональную
проекцию прямой АВ1 на плоскость
(ВВ1D1)
С
А1
( B1 A; A1C1 )
D
AO ( BB1 D1 ) B1O проекция
Д. п.: O1 H B1O
Тогда ( B1 A; A1C1 ) O1 H
А
11.06.2022
О1Н найдем из треугольника В1ОО1
18

19.

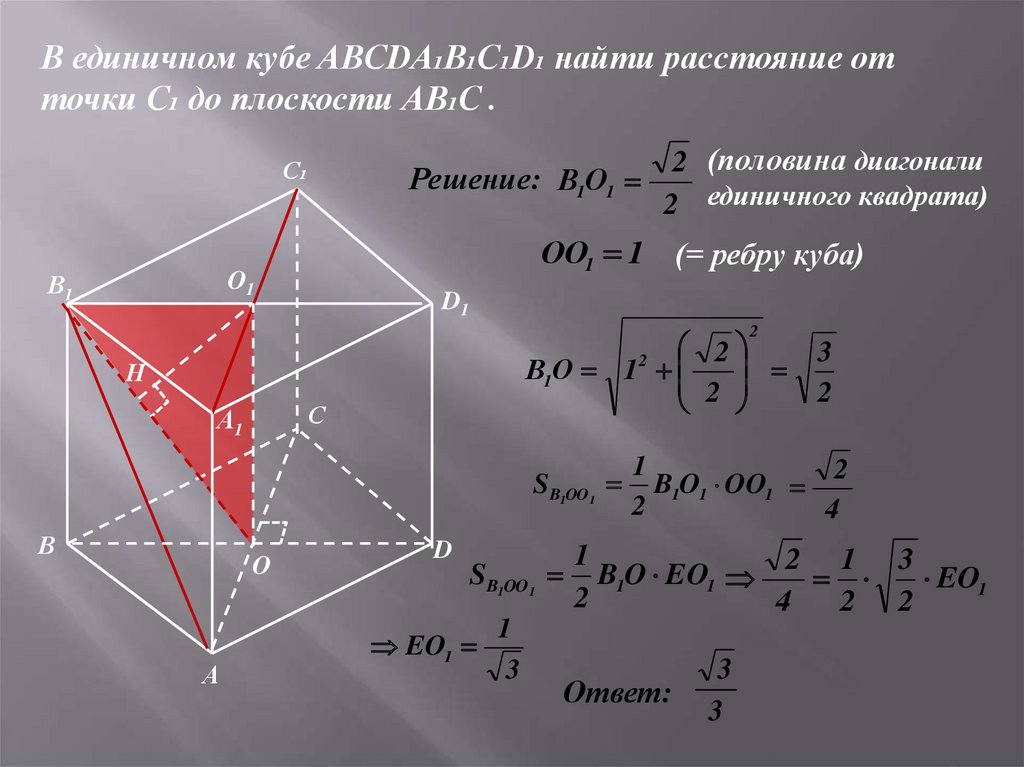
В единичном кубе ABCDA₁B₁C₁D₁ найти расстояние от
точки С₁ до плоскости АВ₁С .
С₁
В1
Решение: В1О1
2 (половина диагонали
2 единичного квадрата)
ОО1 1 (= ребру куба)
O1
D1
2
2
2
В1О 1
2
Н
С
А1
SB1OO 1
В
O
А
D
SB1OO 1
1
EO1
3
3
2
1
2
B1O1 OO1
2
4
1
2 1 3
B1O EO1
EO1
2
4
2 2
Ответ:
3
3

20.

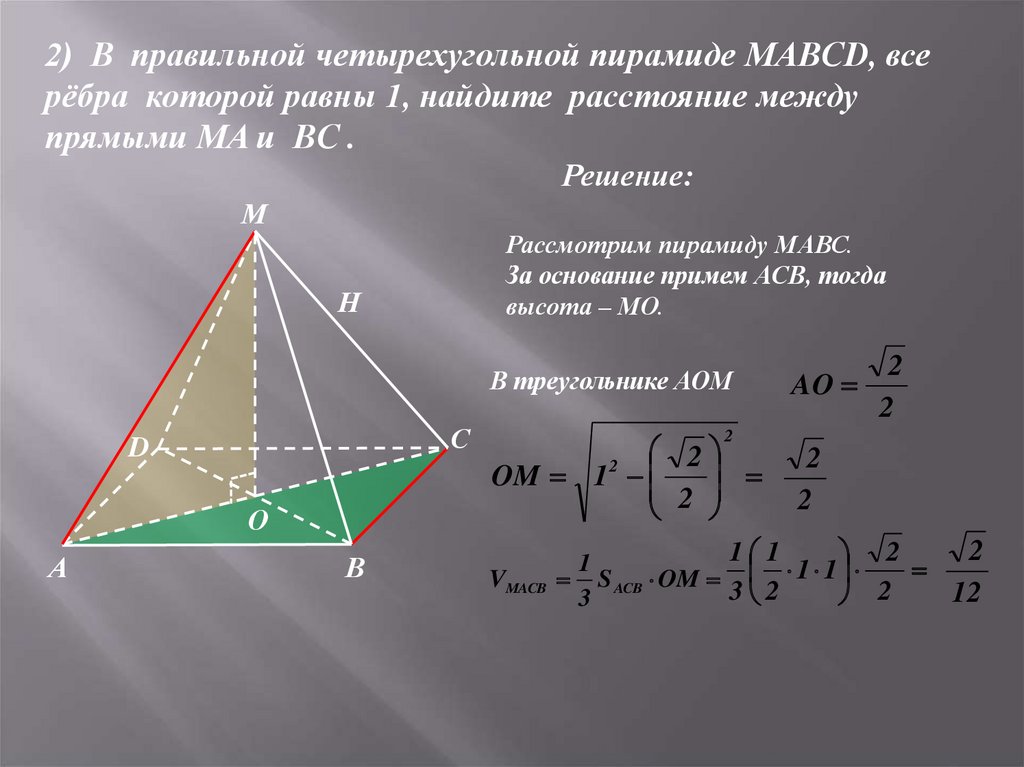
2) В правильной четырехугольной пирамиде MABCD, все
рёбра которой равны 1, найдите расстояние между
прямыми MA и BC .
Решение:
М
Рассмотрим пирамиду МАВС.
За основание примем АСВ, тогда
высота – МО.
Н
В треугольнике АОМ
С
D
А
2
2
OM 1
2
2
О
В
2
AO
2
VMACB
2
2
1 1
2
1
1
1
S ACB OM
3 2
2
3
2
12

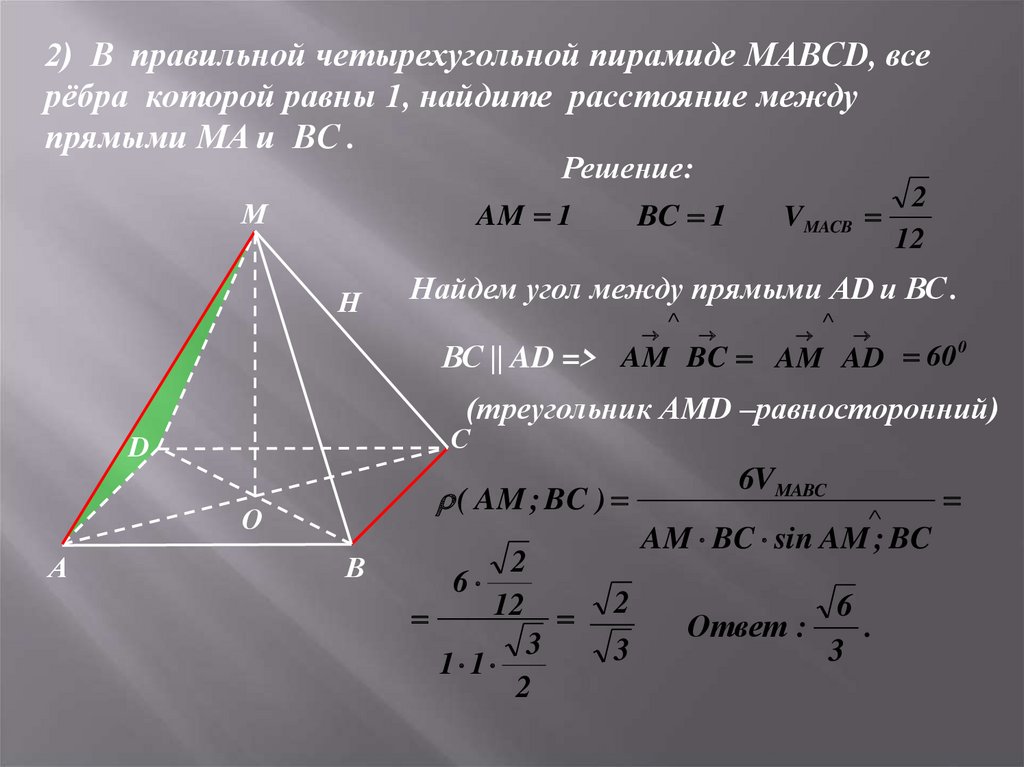
21.

2) В правильной четырехугольной пирамиде MABCD, все
рёбра которой равны 1, найдите расстояние между
прямыми MA и BC .
Решение:
BC 1
AM 1
М
Н
VMACB
2
12
Найдем угол между прямыми АD и ВС .
ВС || AD => AM BC AM AD 60 0
(треугольник АMD –равносторонний)
С
D
( AM ; BC )
О
А
В
2
12
3
1 1
2
6
6VMABC
AM BC sin AM ; BC
2
3
Ответ :
6
.
3