Похожие презентации:
Теория вероятностей. Случайные величины и их характеристики
1. Теория вероятностей
СЛУЧАЙНЫЕ ВЕЛИЧИНЫи их характеристики
2.
3.
4.
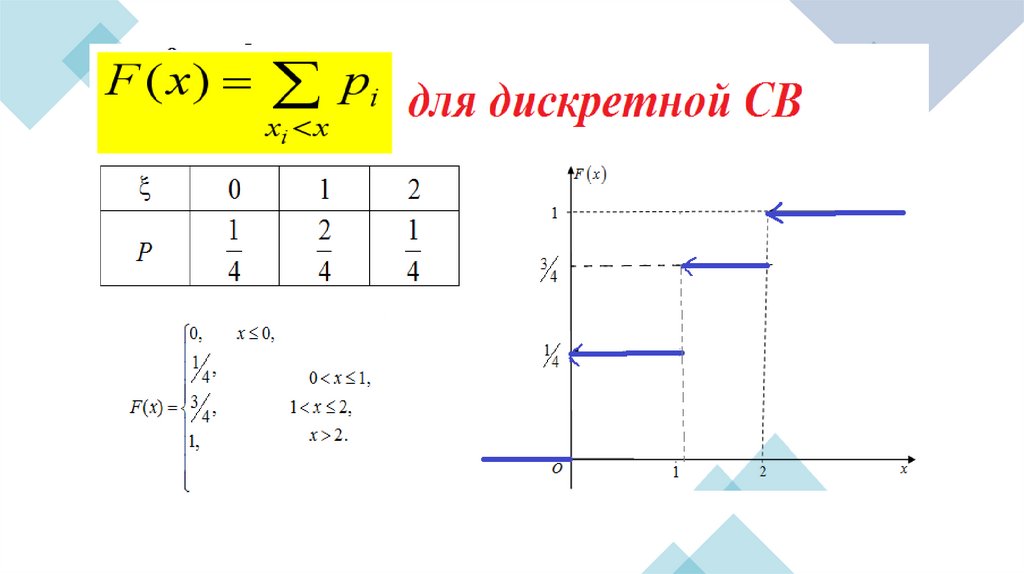
5. Дискретные случайные величины
Для того чтобы задать ДCB , достаточно перечислить все ее возможные значениях1, х2 , , xi , , i 1,2, , и указать, с какими вероятностями pi она их принимает.
Закон распределения ДСВ задают в виде таблицы, называемой рядом
распределения этой СВ:
x2 …
xi …
x1
p1 p2 …
pi …
P
(отметим, что pi 0 , p1 p2 pi 1 – условие контроля)
6.
Функция распределения случайной величины.Универсальным способом задания случайной величины (как дискретной,
так и непрерывной) является функция распределения – вероятность того, что
СВ примет значение, меньшее x :
F ( x) P x , x R,
7.
8.
9.
Числовые характеристики дискретных случайных величин.К
ним
относятся
математическое
ожидание,
дисперсия
и среднее
квадратическое отклонение случайной величины.
Математическим ожиданием дискретной СВ (ее средним значением)
называют
сумму
произведений
значений
случайной
величины
на
соответствующие им вероятности:
M x1 p1 x2 p2
xn pn
Дисперсия СВ – это математическое ожидание квадрата отклонения СВ
от ее математического ожидания:
D M
M 2 ,
характеризует разброс значений СВ вокруг ее математического ожидания.
Для ДСВ эта формула приобретает конкретный вид:
D
n
( xi
i 1
M ) 2 pi
Для вычисления дисперсии удобно также использовать формулу
D M
n
xi2
i 1
Величина
D
M
2
2
pi M .
2
– среднее квадратическое отклонение СВ (от ее
математического ожидания).
10.
11.
12.
Среднее квадратическое отклонение.Для оценки рассеяния возможных значений случайной величины вокруг ее
среднего значения кроме дисперсии служит среднее квадратическое отклонение.
Средним квадратическим отклонением случайной величины называется
квадратный корень из дисперсии D этой величины:
D .
Дисперсия имеет размерность, равную квадрату размерности случайной
величины. Размерность совпадает с размерностью . В тех случаях, когда
желательно, чтобы оценка рассеяния имела размерность случайной величины,
вычисляют среднее квадратичное отклонение, а не дисперсию.
13.
Непрерывные случайные величиныСлучайная величина называется непрерывной (НСВ), если ее функция
распределения F ( x) P( x) непрерывна на всей числовой оси (рисунок 1 в
конце лекции). НСВ принимает все значения из некоторого интервала или
системы интервалов на числовой оси. Вероятность того, что НСВ примет
фиксированное значение, равна нулю, т. е. P( x0 ) 0 .
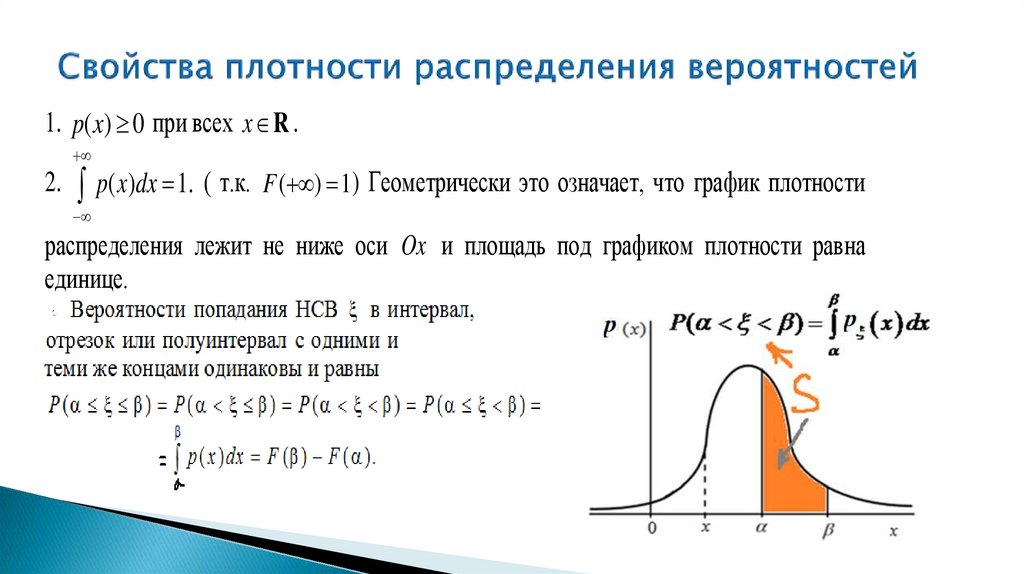
14. Свойства плотности распределения вероятностей
1. p( x) 0 при всех x R .2.
p( x)dx 1. ( т.к.
F ( ) 1 ) Геометрически это означает, что график плотности
распределения лежит не ниже оси Ox и площадь под графиком плотности равна
единице.
15.
Числовые характеристики непрерывной случайной величиныДля НСВ числовыми характеристиками также являются математическое
ожидание, дисперсия и среднее квадратическое отклонение.
Математическое ожидание M и дисперсия D НСВ определяются по
формулам
M
x p( x)dx,
D
x M
2
p( x)dx ,
где интегралы предполагаются абсолютно сходящимися.
На практике для вычисления дисперсии удобно использовать формулу
2
D M 2 M , при этом
M ( 2 )
x 2 p( x )dx .
Среднее квадратическое отклонение определяется формулой
D .
16.
Пример. Найти a, p(x), M , D , , P(–1 < 2,5), P( = 3,5), если данафункция распределения
0,
2
F ( x) a(x 1),
1,
x 1,
1 x 3,
x 3.
Построить графики функции распределения и плотности распределения.
17.
Используем свойство плотностиp( x )dx 1.
Найдем плотность
вероятности p(x) как производную от функции распределения F(x):
0,
p( x) F '( x) 2ax,
0,
Вычислим
1
.
8
3
p( x )dx 2axdx ax
1
2 3
1
x 1,
1 x 3,
x 3.
8a, т. е. 8a = 1. Следовательно, a =
18.
Подставляя найденное a, получим следующие выражения для функциираспределения и плотности распределения данной СВ:
0,
1 2
F ( x) 8 (x 1),
1,
0,
p( x) 4x ,
0,
x 1,
1 x 3,
x 3;
x 1,
1 x 3,
x 3.
19.
Вычисляем числовые характеристики:3 3
x
x
x
27 1 13
;
M xp( x )dx x dx dx
4
12 1
12
6
1
1 4
3
3
2
4 3
x
x
x
81 1
M x p( x )dx x dx dx
5;
4
16 1
16
1
1 4
2
3
2
3
3
2
169 11
;
D M M 5
36 36
2
2
11
11
.
среднее квадратическое отклонение равно D
36
6
20.
Вероятность можно вычислить с помощью функции распределения:1
21
2
P(–1 < 2,5) = F(2,5) – F(–1) = ((2,5) 1) 0
0,65625.
8
32
Или можно воспользоваться интегралом от плотности распределения
вероятностей:
P(–1 < 2,5) =
2,5
1
1
2,5
1
1
p( x)dx 0 dx
2 2,5
x
x
dx
4
8
1
6,25 1
0,65625
8
8
Для непрерывной СВ вероятность того, что она примет конкретное
значение, равна нулю, т. е. P( = 3,5) = 0.
21.
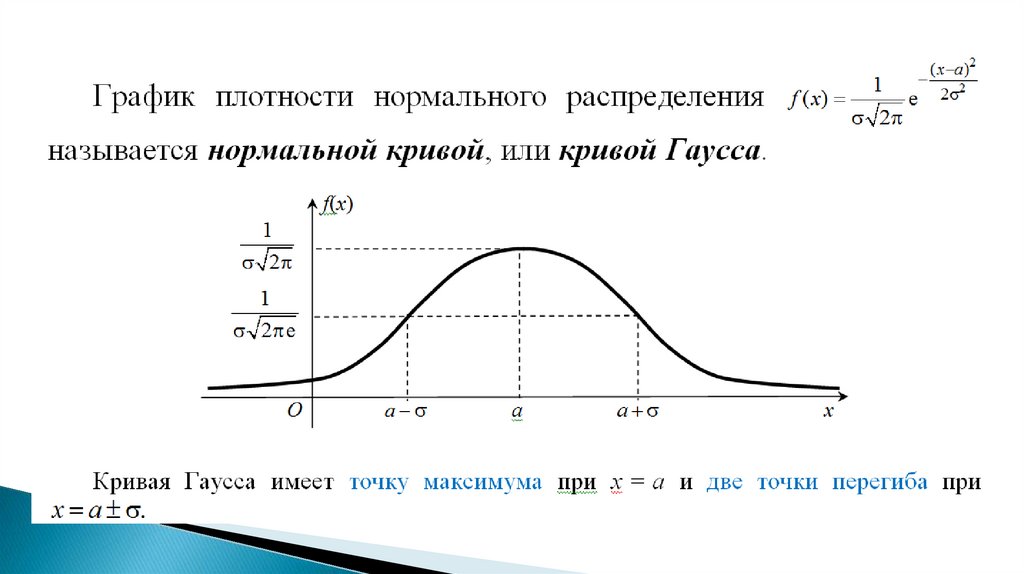
Распределение НСВ называется нормальным (или распределениемГаусса) с параметрами a и > 0: N (a, ) , если плотность распределения
вероятностей имеет вид
1
p( x)
e
2
( x a )2
2 2
,
x ( , ).
Параметры a и имеют смысл математического ожидания и среднего
квадратического отклонения СВ : M a, D 2 , .
22. Основные распределения ДСВ
23. Основные распределения НСВ
24.
25.
26.
Вероятность попадания нормально распределенной СВ на заданный интервал( , ) можно найти по формуле:
a
a
P( )
.
Вероятность того, что СВ , распределенная нормально с параметрами a и
, отклонится от своего математического ожидания менее, чем на δ,
определяется соотношением
P( a ) 2 .
27.
28.
Пример. СВ распределена по нормальному закону. Математическоеожидание M = 5; дисперсия D = 0,64. а) Найти вероятность попадания этой
СВ в интервал (4;7). б) Какова вероятность того, что СВ примет значение,
большее чем 3? в) Определить вероятность того, что СВ примет значение,
равное ее математическому ожиданию.
а) Так как a = M = 5; D = 0,8, то
7 5
4 5
P(4 < < 7) =
0,8
0,8
2,5 1,25 0,4938 ( 0,3944) 0,8882.
29.
aa
P( )
.
б) Найдем
5
3 5
P( > 3) = P(3 < < + ∞) =
0,8
0,8
2,5 0,5 ( 0,4938) 0,9938.
в) Поскольку нормальное распределение является непрерывным
распределением, то вероятность того, что СВ примет конкретное значение,
равна 0, т. е. P( = M ) = P( = 5) = 0.



























 Математика
Математика








