Похожие презентации:
Электрический диполь
1. ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ
Электрическийдиполь – это система
двух одинаковых по модулю
разноименных точечных зарядов,
находящихся на расстоянии
(плечо
диполя) друг от друга
-Q
P
+Q
P
- Дипольный
момент
P Q
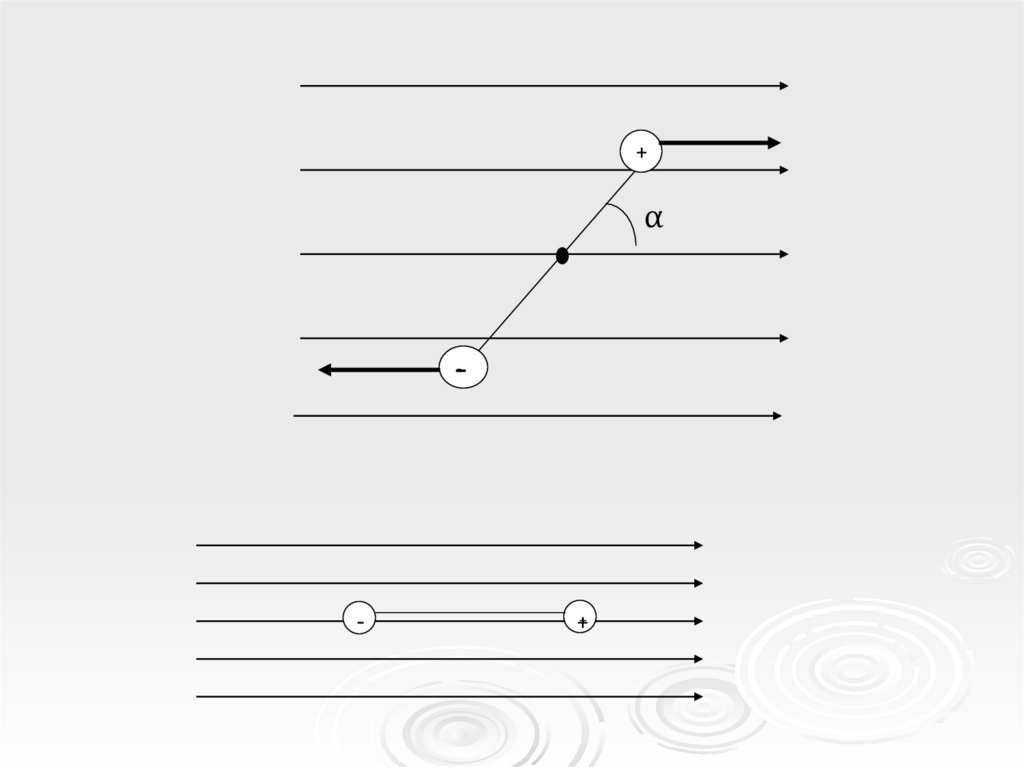
2.
+α
-
--
++
3.
Надиполь действует момент сил,
который стремится развернуть его
вдоль поля
M r qE
l
M qE sin
2
Моменты
M r qE
l
M qE sin
2
сил направлены в одну
сторону
M M M
4.
M M MM M M
l
M 2 qE sin qlE sin PE sin
2
M P E
Диполь будет поворачиваться к положению
устойчивого равновесия ,
(ориентация вдоль поля)
5. ПОЛЯРИЗАЦИЯ
Поляризацией называется процессориентации диполей или появление
ориентированных по полю диполей под
воздействием внешнего электрического
поля
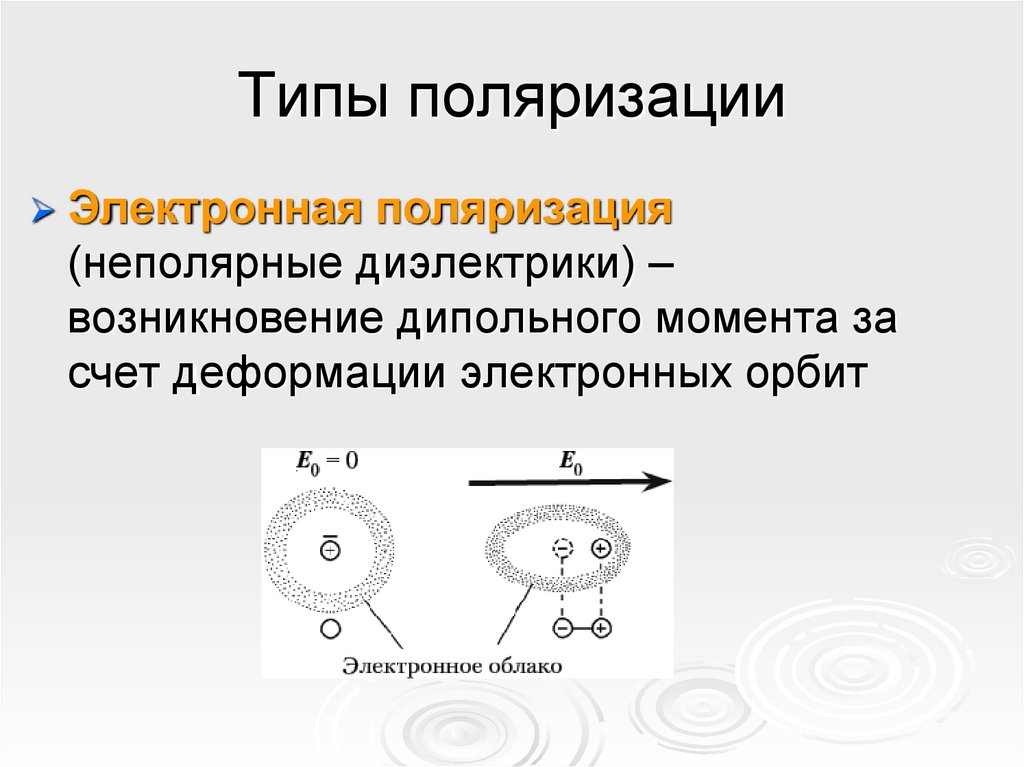
6. Типы поляризации
Электроннаяполяризация
(неполярные диэлектрики) –
возникновение дипольного момента за
счет деформации электронных орбит
7.
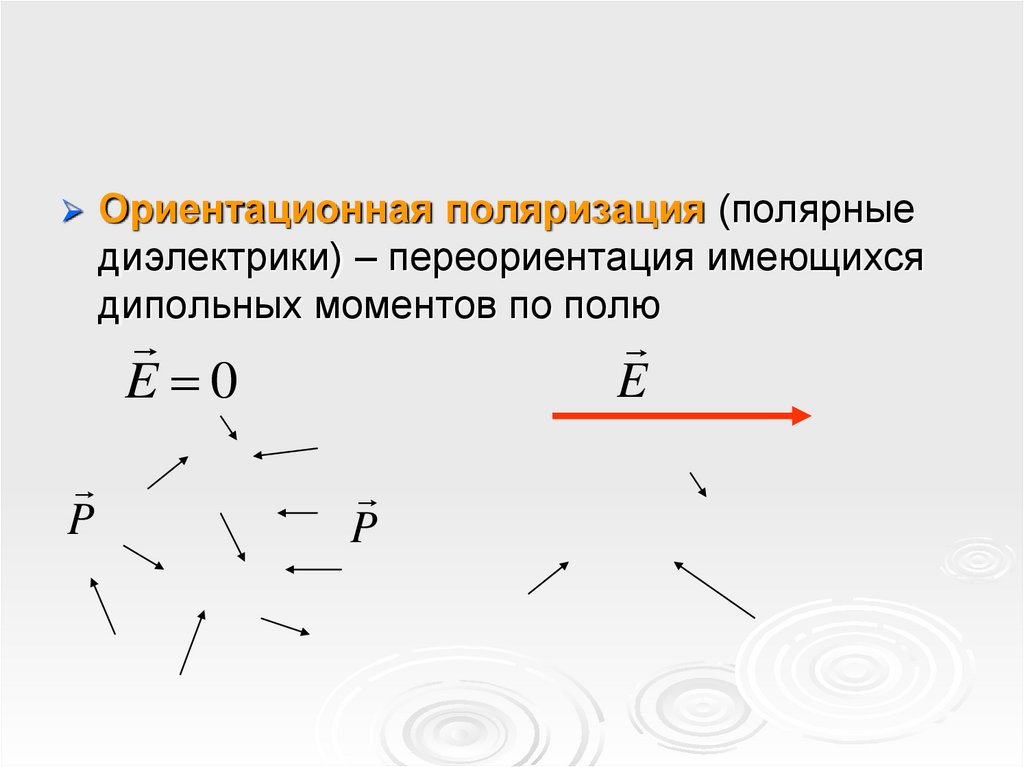
Ориентационная поляризация (полярныедиэлектрики) – переориентация имеющихся
дипольных моментов по полю
E 0
P
E
P
8.
Ионнаяполяризация ( ионные
кристаллы) заключается в смещении
подрешеток положительных ионов по
полю, а отрицательных – против поля
9. ПОЛЯРИЗОВАННОСТЬ
Поляризованность– это дипольный
момент единицы
объема
pi
N
P
p
i 1
V
- Дипольный момент одной молекулы
i
10.
Для большинствадиэлектриков
Ρ 0 E
Диэлектрическая восприимчивость
11.
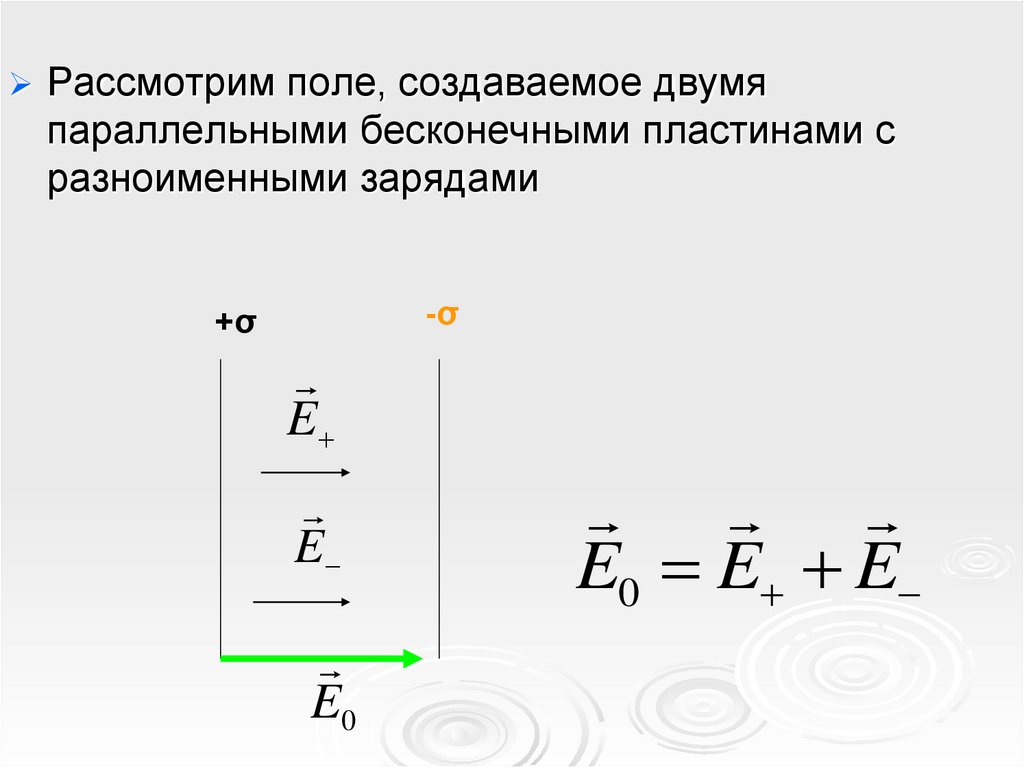
Рассмотрим поле, создаваемое двумяпараллельными бесконечными пластинами с
разноименными зарядами
-σ
+σ
E
E
E0
E0 E E
12.
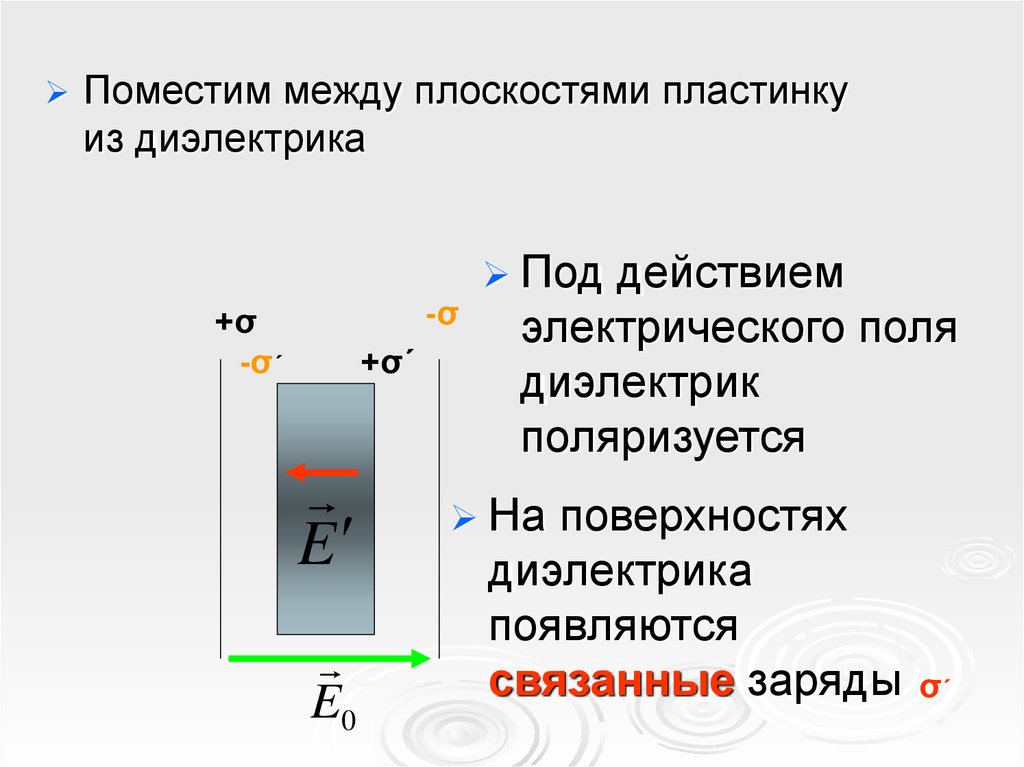
Поместим между плоскостями пластинкуиз диэлектрика
Под
-σ
+σ
-σ΄
+σ΄
E
E0
действием
электрического поля
диэлектрик
поляризуется
На
поверхностях
диэлектрика
появляются
связанные заряды
σ΄
13.
Связанныезаряды- это
нескомпенсированные заряды,
появляющиеся в результате
поляризации диэлектрика
14.
Результирующееполе внутри
диэлектрика
E
0
Q S
p
E E0 E
E E0 E E0
0
Q d S d p
- дипольный момент пластинки диэлектрика
15.
С другой стороныp P V P S d
p S d P S d
P
Т.е. поверхностная плотность связанных
зарядов – это поляризованность
16.
PE E0
E0
0
0
P 0 E
0 E
E0 E
E E0 E0
0
0
E0 E0
E
1
1
P
диэлектрическая проницаемость
вещества
17.
Диэлектрическаяпроницаемость
показывает во
сколько раз
электрическое поле
ослабляется
диэлектриком по
сравнению с полем
в вакууме
E
E0
18.
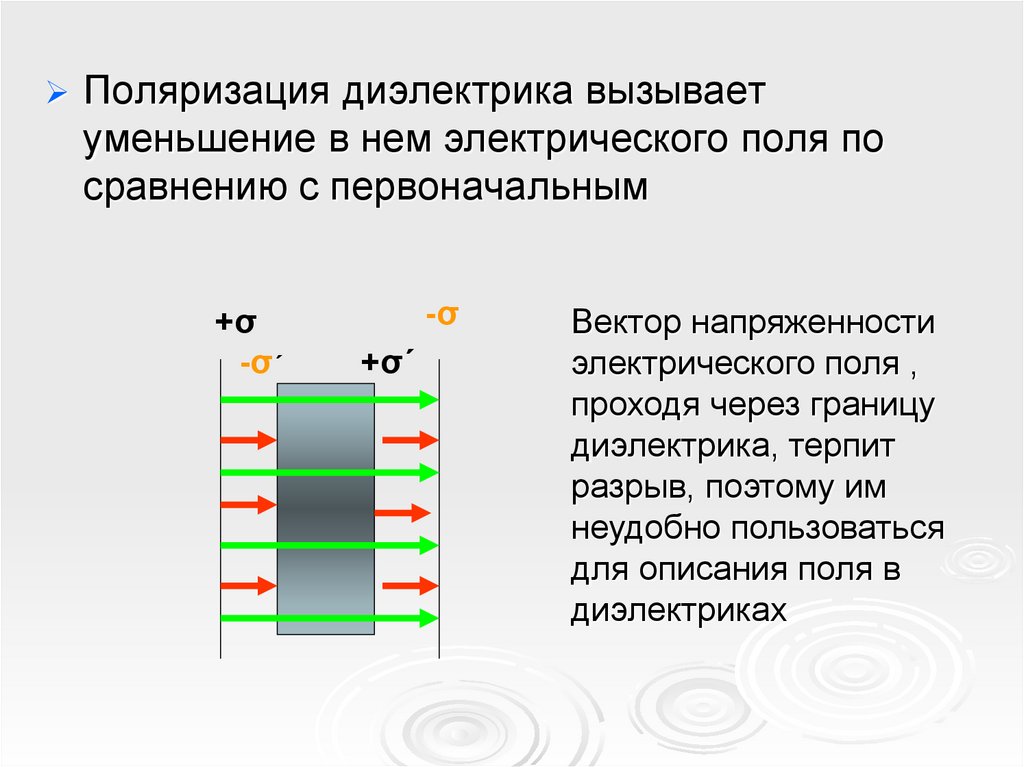
Поляризация диэлектрика вызываетуменьшение в нем электрического поля по
сравнению с первоначальным
+σ
-σ΄
-σ
+σ΄
Вектор напряженности
электрического поля ,
проходя через границу
диэлектрика, терпит
разрыв, поэтому им
неудобно пользоваться
для описания поля в
диэлектриках
19. ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ
20.
Полев диэлектрике уменьшается по
сравнению с полем в вакууме
Линии напряженности разрываются на
поверхности диэлектрика
21.
Теорема Гаусса дляполя в диэлектрике
Qin
E dS
S
0
Q Q
in
in
0
Q – свободные заряды в диэлектрике
Q́ – связанные заряды в диэлектрике, как их
искать ?
22. Вектор электрического смещения
D 0 ED (1 ) 0 E 0 E 0 E
D P 0E
Размерность
Кл/м2
23.
DПоле
изображается с помощью
линий электрического смещения
Линии электрического смещения
начинаются и заканчиваются только на
свободных зарядах
Линии напряженности начинаются и
заканчиваются и на свободных зарядах,
и на связанных
24. ТЕОРЕМА ГАУССА ДЛЯ ЭЛЕКТРИЧЕСКОГО СМЕЩЕНИЯ
Поток вектораэлектрического
смещения через
замкнутую
S
поверхность равен
алгебраической
сумме свободных
зарядов,
заключенных внутри
данной поверхности
D dS Qin
25. ВАКУУМ
Для вакуума ε=1D 0E
S
E
d
S
Q
0
in
S
D dS Qin
Qin
E dS
S
0
Теорема Гаусса для электрического смещения
переходит в теорему Гаусса для напряженности
26. Пример
Точечный заряд q помещен внутри шара изоднородного диэлектрика с проницаемостью ε.
Найти зависимость напряженности от расстояния до
центра шара. Радиус шара R.
D dS Qin
S
+q
r R, r R
2
D dS D 4 r q
S
q
D
2
4 r
27.
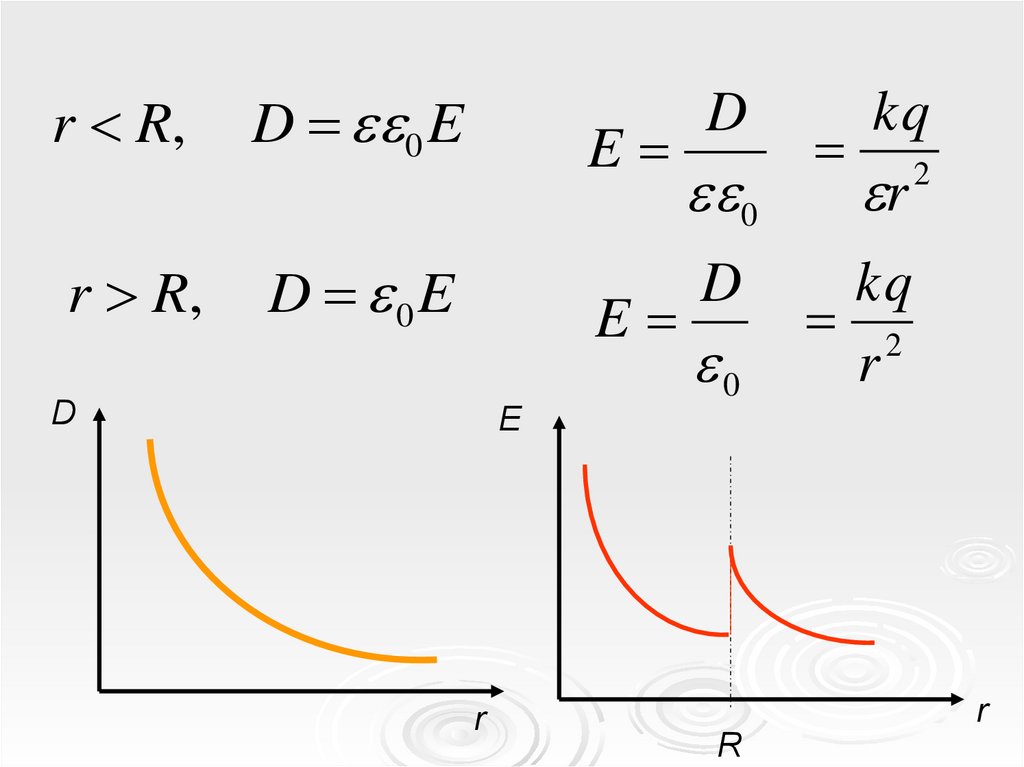
r R,D 0 E
r R,
D 0E
E
E
D
D
0
D
0
kq
2
r
kq
2
r
E
r
r
R
28. УСЛОВИЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ ДИЭЛЕКТРИКОВ
29.
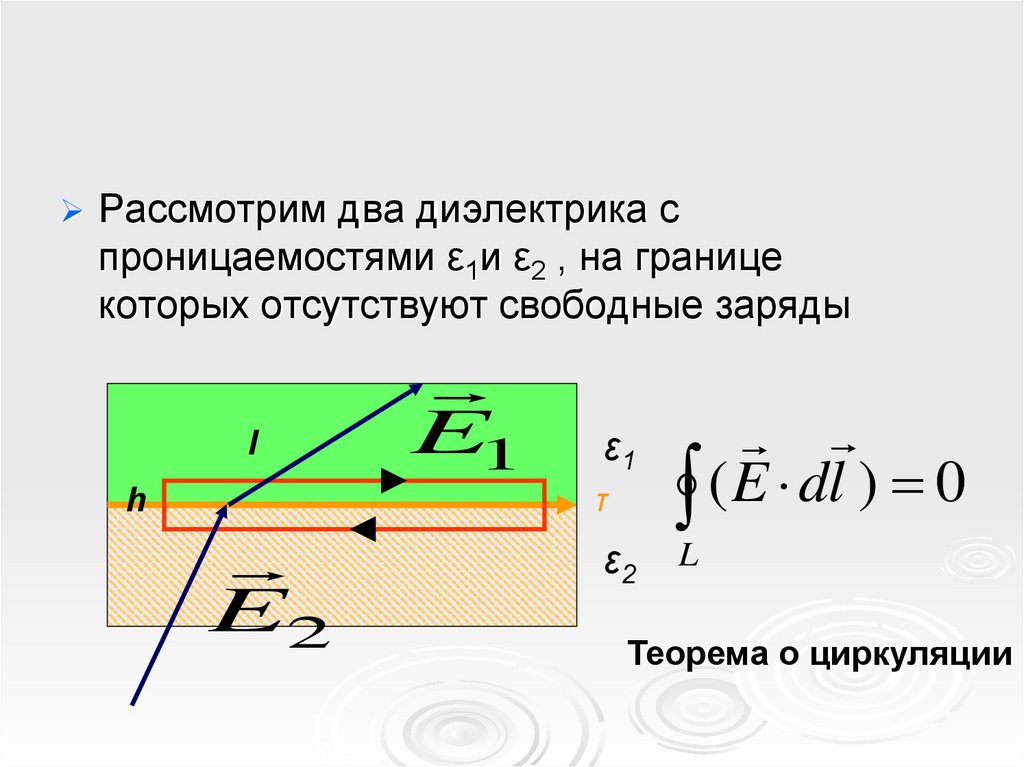
Рассмотрим два диэлектрика спроницаемостями ε1и ε2 , на границе
которых отсутствуют свободные заряды
l
E1
ε1
τ
h
E2
ε2
( E dl ) 0
L
Теорема о циркуляции
30.
h 0 ( E dl ) E 1 E 2 0L
E 1 E 2
D 1 E 1 1 0 D 2 E 2 2 0
D 1 D 2
1
2
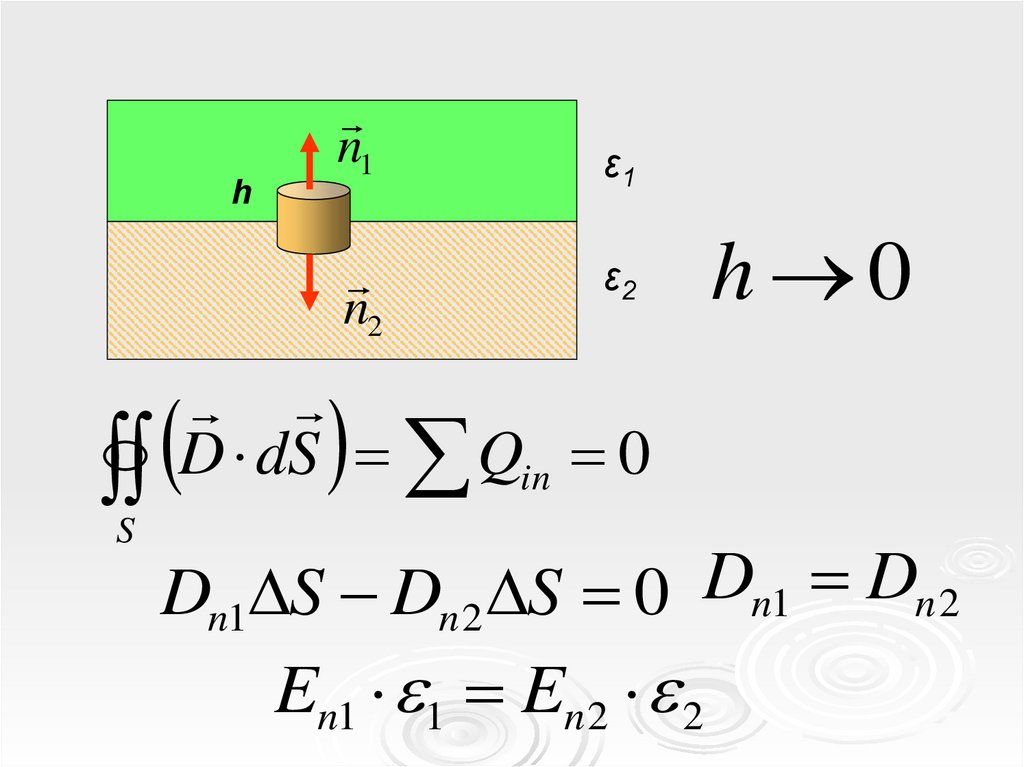
31.
hn1
n2
ε1
ε2
h 0
D dS Qin 0
S
Dn1 S Dn 2 S 0 Dn1 Dn 2
En1 1 En 2 2
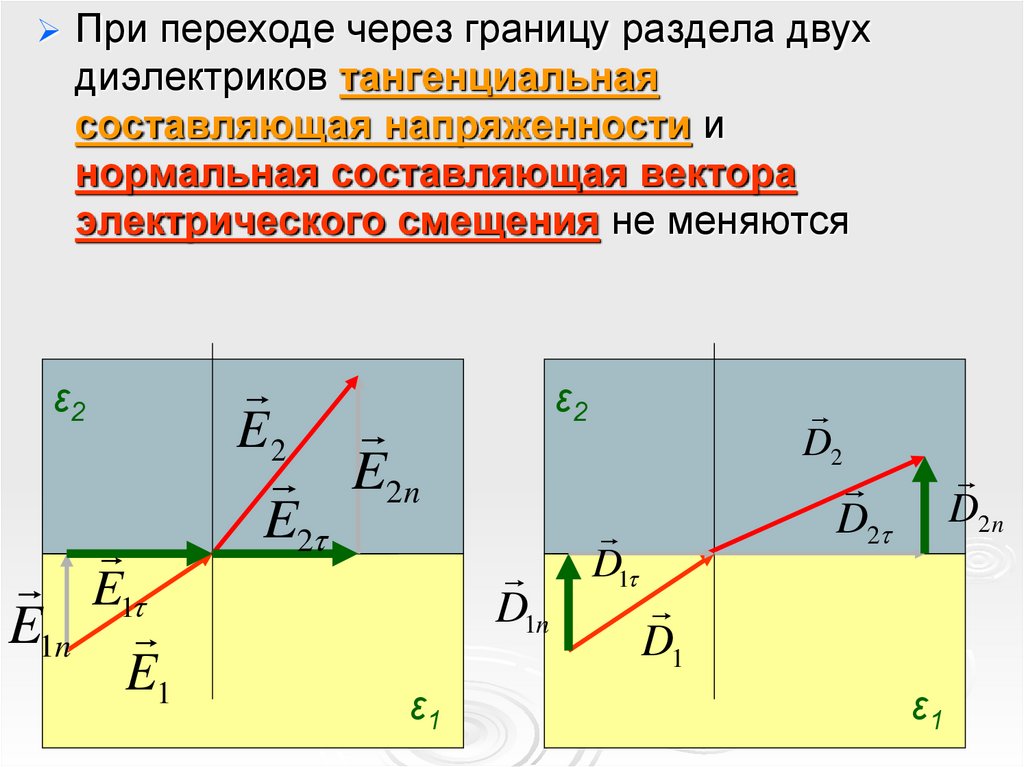
32.
При переходе через границу раздела двухдиэлектриков тангенциальная
составляющая напряженности и
нормальная составляющая вектора
электрического смещения не меняются
ε2
E1n
E1
E1
E2
E2n
E2
ε1
ε2
D1n
D2
D1
D2 n
D2
D1
ε1
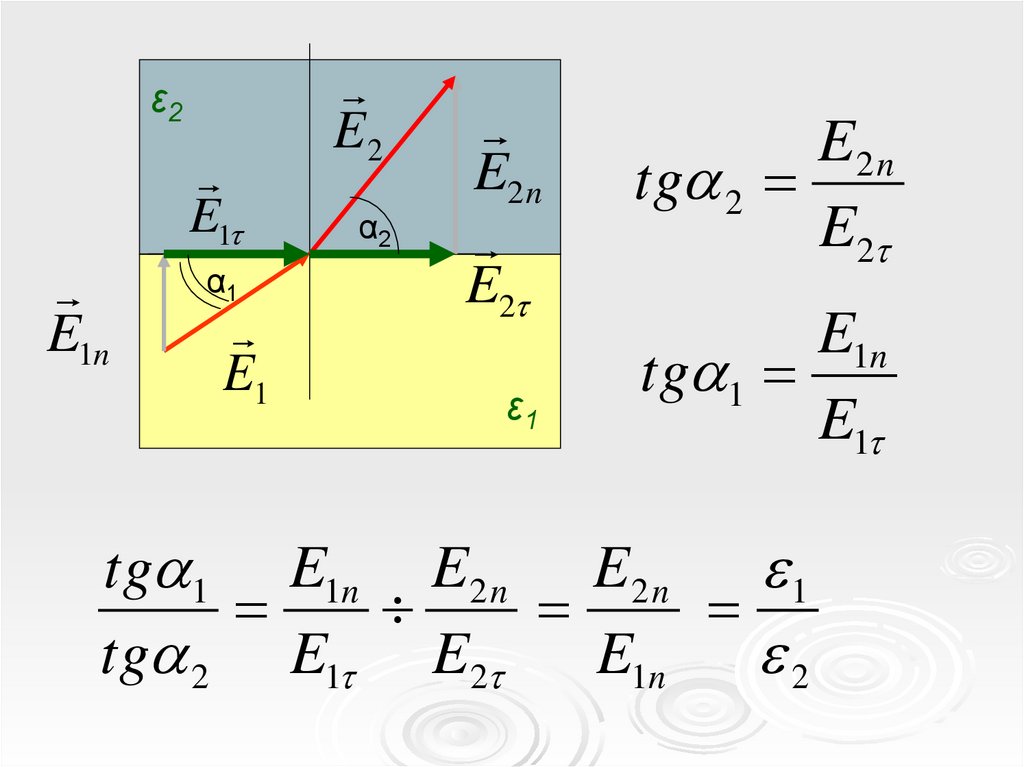
33.
ε2E1
E1n
α1
E1
E2
α2
E2n
E2
ε1
E2 n
tg 2
E2
E1n
tg 1
E1
tg 1 E1n E2 n E 2 n
1
tg 2 E1 E2
E1n
2





















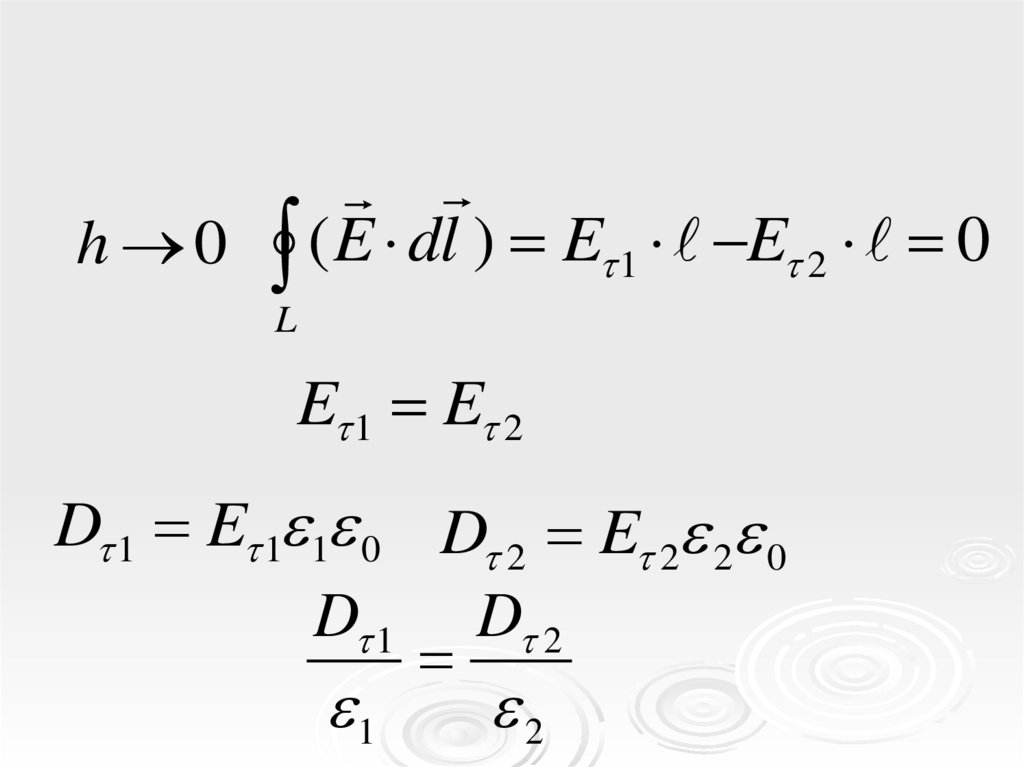
 Физика
Физика








