Комплексные числа

1. 4

Комплексные числа:
определение;
геометрическое изображение
комплексного числа;
формы записи комплексного числа;
операции
над
комплексными
числами.

2. Решить уравнение: Решение:

Решить уравнение:
z 2 z 10 0
2
Решение:
z1, 2
2 4 40 2 36 2 36 1
2
2
2
Обозначим 1 i мнимая единица i 2 1
i i; i 1; i i и т.д.
3
z1, 2
4
5
2 6i 2(1 3i )
1 3i
2
2

3. Определение. Комплексным числом называется выражение вида где - действительные числа , мнимая единица. Число действительная часть комплек

Определение.
Комплексным числом называется выражение вида
z x iy
где x, y - действительные числа , i мнимая
единица. Число x действительная часть
комплексного числа z и обозначается Re( z ) , а y
мнимая часть и обозначается
Im( z ) , т.е.
x Re z , y Im z.

4. Алгебраическая форма записи комплексного числа

1. Два комплексных числа
z1 x1 iy1 и z2 x2 iy2
равны, если
x1 x2 ; y1 y2
2. Z = 0, если x=0; y=0
3. Если y=0, то z R.
4. Числа z1 x1 iy1 и z2 x1 iy1
сопряженными и обозначаются
называются
z иz

5.

Такая форма записи комплексного числа
называется алгебраической.
Изображается комплексное число точкой на
комплексной плоскости.
z1 1 3i, z2 1 3i, z3 2i, z4 2 i
Imz
.z
3
1
.z
4
Rez
.z
-3
3
.z
2

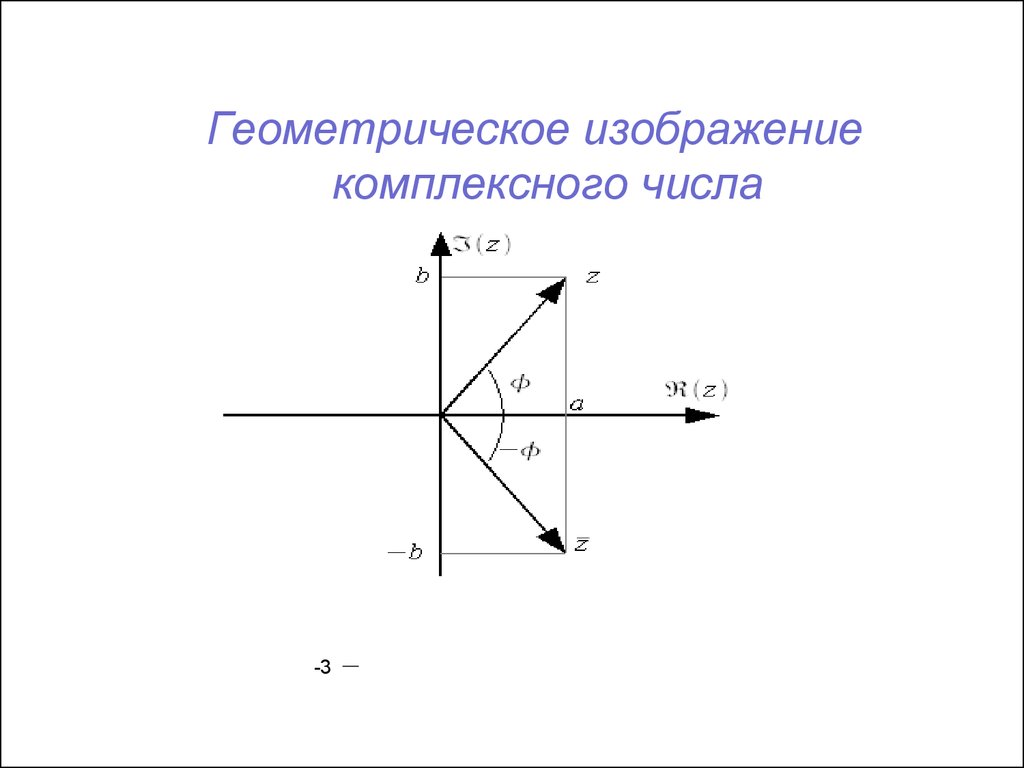
6.

Геометрическое изображение
комплексного числа
Для геометрического представления комплексных
чисел служат точки координатной плоскости OXY.
Плоскость называется комплексной , если каждому
z x iy соответствует
комплексному числу
точка плоскости3 z ( x; y ) , причем это соответствие
взаимно однозначно.
Оси OX и OY, на которых расположены действительные числа
z x 0i x
z 0 iy iy,
и чисто мнимые числа
называются
соответственно
действительной и мнимой осями.
-3

7.

Геометрическое изображение
комплексного числа
3
-3

8. Тригонометрическая форма записи комплексного числа

Imz
z
y
r
φ
x
r
Rez
x r cos
z x iy
y r sin
r cos i r sin
r (cos i sin )
r (cos( 2 n) i sin( 2 n))
x 2 y 2 z модуль числа z
y
tg
; arg z аргумент числа z
x
0 2

9. Показательная форма записи комплексных чисел Из формулы Эйлера

i
e cos i sin
i
z z (cos i sin ) z e

10. Показательная форма записи комплексных чисел Из формулы Эйлера

i
e cos i sin
i
z z (cos i sin ) z e

11. Пример. z=-1-i записать в тригонометрической и показательной формах. Решение.

x 1
2
2
2
2
z x y ( 1) ( 1) 2
y 1
y 1
5
tg
1
x 1
4
5
i
5
5
z 1 i 2 (cos i sin ) 2e 4
4
4

12. Операции над комплексными числами z0=x0+iy0 и z1=x1+iy1

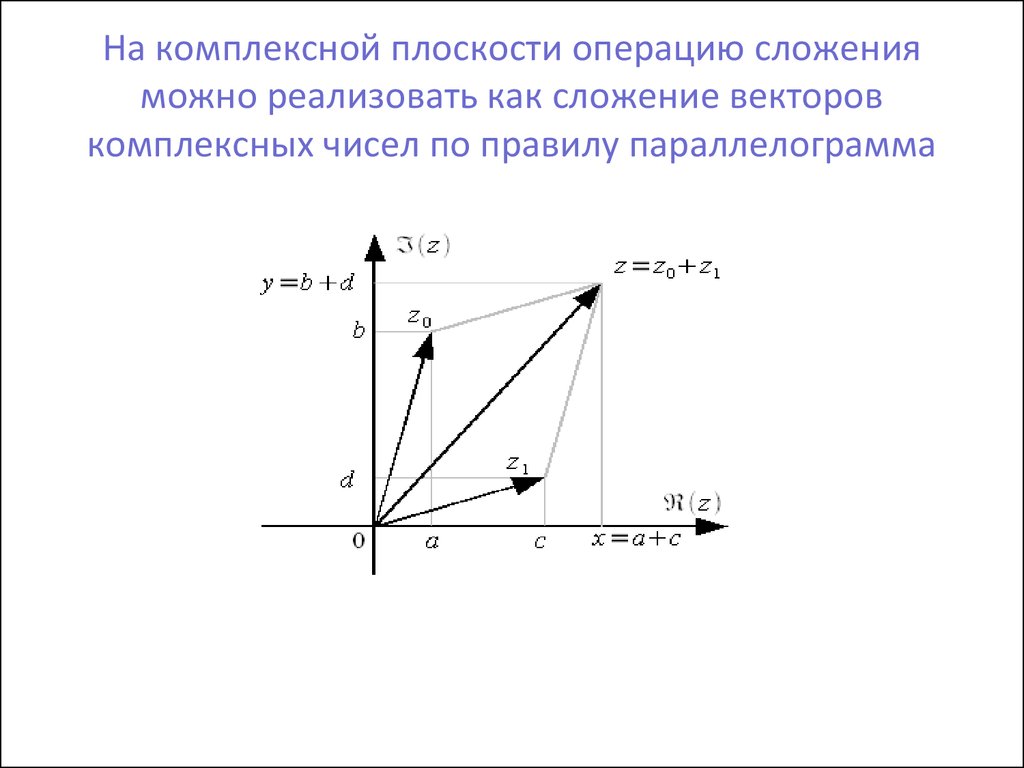
Сумма двух комплексных чисел и есть также
комплексное число :z0 + z1 =(x0+x1)+i(y0+y1)
Пример: (3+2i)+(1+5i)=(3+1)+i(2+5)=4+7i.
Как следует из выражения при сложении реальные
и мнимые части комплексного числа также
складываются.

13. На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма

14. 2.Вычитание комплексных чисел

Разность двух комплексных чисел и есть также комплексное число:
z0 - z1 =(x0-x1)+i(y0-y1).
Пример:
(4+i)-(-2-i)=(4+2)+i(1+1)=6+2i.
На комплексной плоскости операцию
вычитания можно реализовать как
вычитание векторов комплексных
чисел по правилу параллелограмма .
На первом шаге из вектора
формируется вектор
после чего вектор
с вектором
,
складывается
по правилу параллелограмма.

15. 3. Умножение комплексных чисел. Для того чтобы получить формулу для умножения комплексных чисел необходимо перемножить два комплексных чи

3. Умножение комплексных чисел.
Для того чтобы получить формулу для умножения
комплексных чисел необходимо перемножить два
комплексных числа по правилу умножения многочленов:
z1 · z2=(x1x2-y1y2)+i(x1y2+x2y1).
Пример 1.
(1+3i)(-5-2i)=-5-15i-2i-6i2 =-5-17i+6=
=1-17i .
Пример 2.
(1+3i)(1-3i)=1-3i+3i-9i2 =1+9=10 .
z z
всегда действительное число

16. 4. Деление комплексных чисел Пример

4. Деление комплексных чисел
z1
z такое, что z z2 z1
z2
Пример
4 i
(4 i )(3 2i ) 12 3i 8i 2i
3 2i (3 2i )(3 2i )
9 4
14 5i 14 5
i
13
13 13
2

17. 5. Операции над комплексными числами, заданными в тригонометрической форме. 1. 2. 3. 4.

5. Операции над комплексными числами, заданными в
тригонометрической форме.
1.
2.
3.
z1 z 2 z1 z 2 (cos( 1 2 ) i sin( 1 2 ))
z1
z1
(cos( 1 2 ) i sin( 1 2 )) (| z 2 | 0)
z2
z2
z z (cos n i sin n ); n N
n
n
4.
n
z
n
2 k
2 k
z cos
i sin
; k 0;1;2;...n 1
n
n