Энергия. Работа. Закон сохранения механической энергии

1. Энергия. Работа. Закон сохранения механической энергии

Лекция 1

2. План лекции

CEE
Энергия как универсальная мера различных форм движения
и взаимодействия.
Работа силы.
Консервативные и диссипативные силы.
Потенциальная энергия системы материальных точек.
Потенциальная энергия растянутой пружины.
Потенциальная энергия гравитационного притяжения двух
материальных точек.
Потенциальная энергия тела в однородном поле силы
тяжести Земли.
Кинетическая энергия.
Закон сохранения энергии в механике.
Общефизический закон сохранения энергии.

3.

Энергия как универсальная мера различных
форм движения и взаимодействия
CEE

4.

Работа постоянной силы на
прямолинейном пути
CEE
Изменение
механического
движения тела
вызывается
силами,
действующими на
него со стороны
других тел.

5.

Работа постоянной силы на
прямолинейном пути
CEE
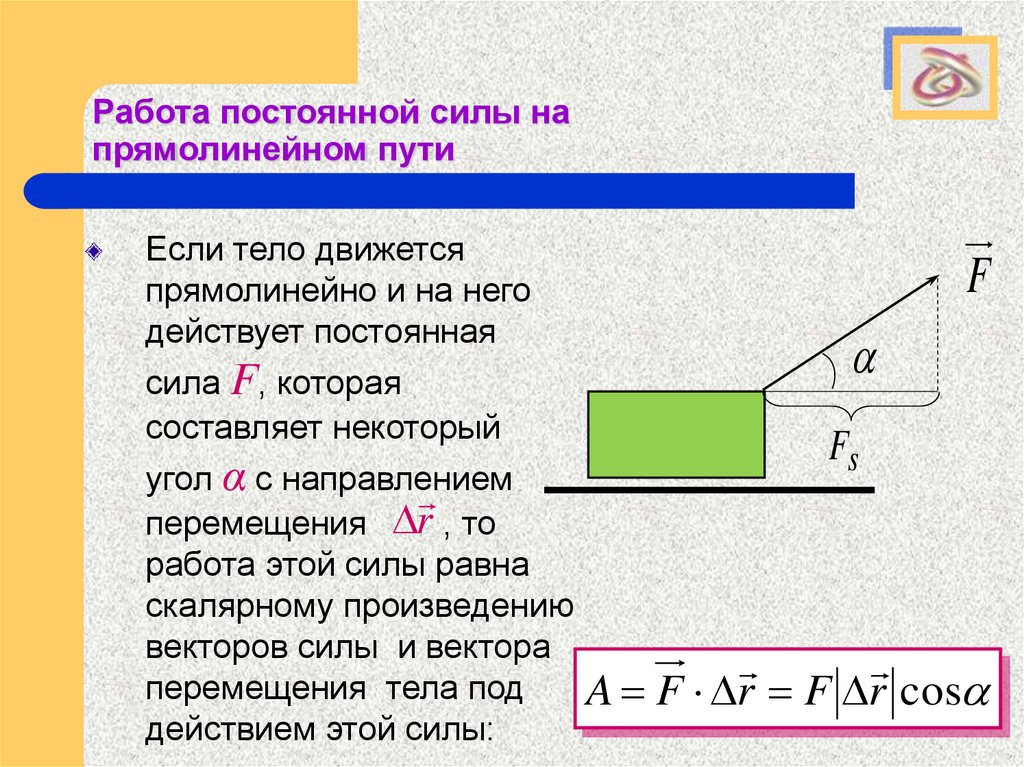
Если тело движется
прямолинейно и на него
действует постоянная
сила F, которая
составляет некоторый
угол α с направлением
перемещения r , то
работа этой силы равна
скалярному произведению
векторов силы и вектора
перемещения тела под
действием этой силы:
F
Fs
A F r F r cos

6.

Работа постоянной силы на
прямолинейном пути
CEE
При
прямолинейном
движении
вектор
перемещения совпадает с соответствующим
участком траектории и модуль перемещения
равен пройденному пути:
r s

7.

Работа постоянной силы на
прямолинейном пути
CEE
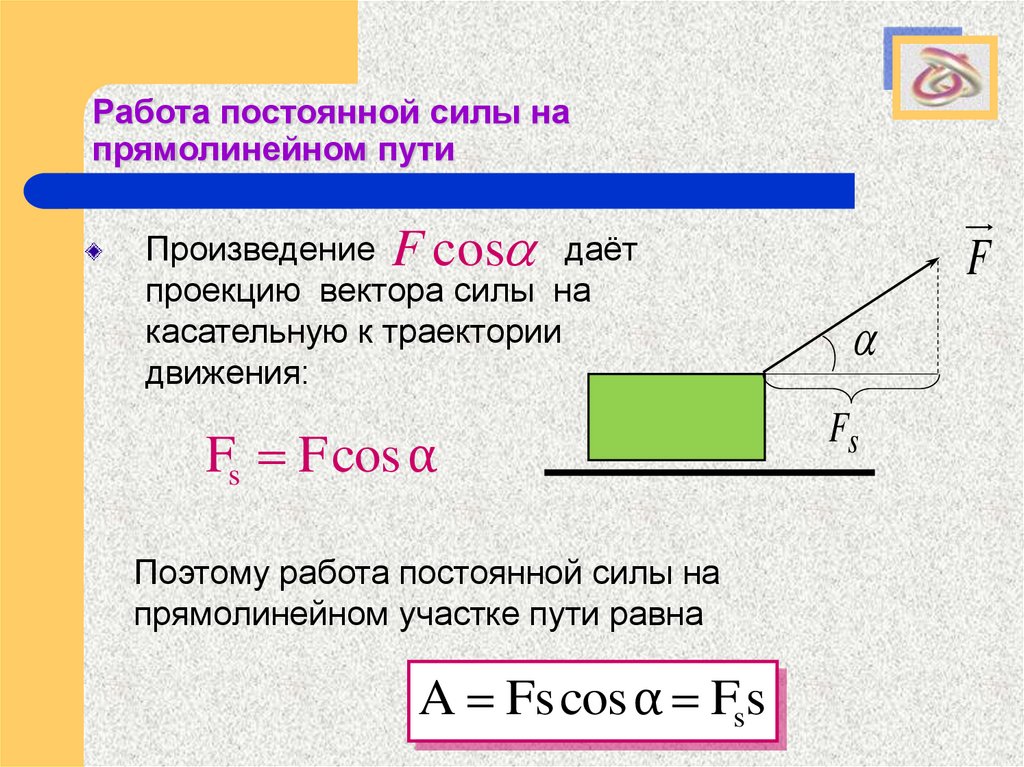
Произведение F cos
даёт
проекцию вектора силы на
касательную к траектории
движения:
Fs F cos α
Поэтому работа постоянной силы на
прямолинейном участке пути равна
A Fs cos α Fss
F
Fs

8.

Работа постоянной силы на
прямолинейном пути
CEE
Единицей
работы
в
СИ
служит
работа,
совершаемая на пути в один метр с силой в один
ньютон,
действующей
в
направлении
перемещения.
Эта единица называется джоулем (Дж),
т.е.
1 Дж = 1 Н 1м = 1 кг·м2/с2.

9.

Работа постоянной силы на
прямолинейном пути
CEE
Fs
С геометрической точки
зрения работа А численно
равна площади фигуры,
заключенной под
графиком зависимости Fs
от пройденного пути s .
A=Fss
s

10.

Работа силы на криволинейном пути
CEE
F
dr
1
α
Fs
υ
2
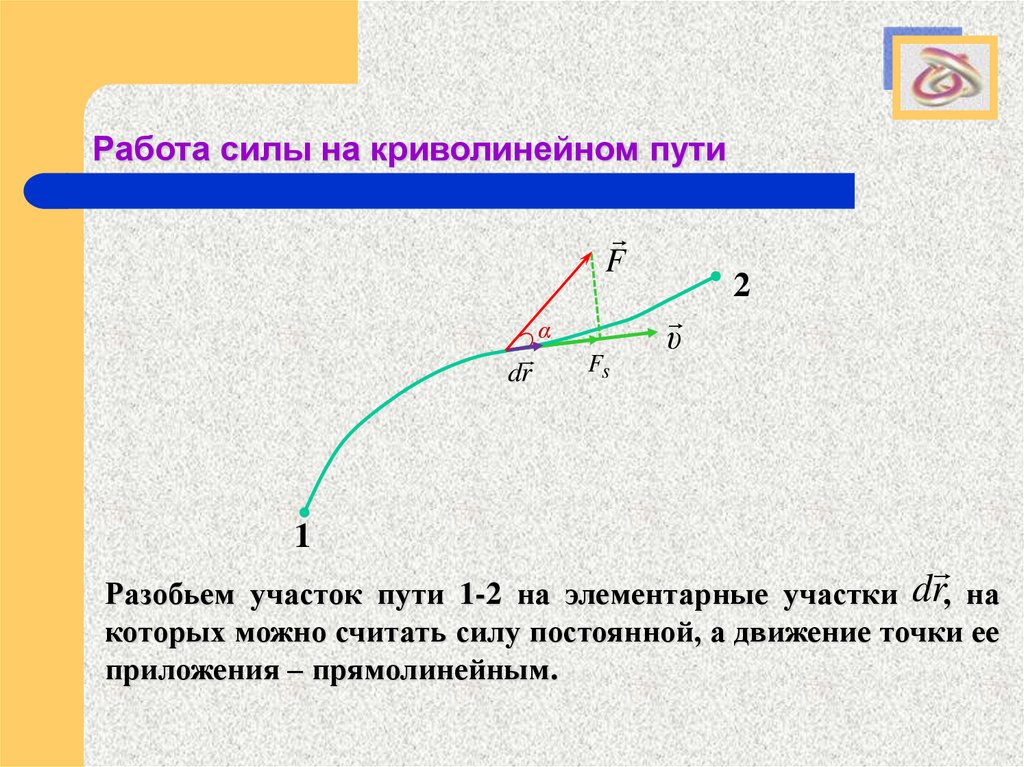
dr,
Разобьем участок пути 1-2 на элементарные участки
на
которых можно считать силу постоянной, а движение точки ее
приложения – прямолинейным.

11.

Работа силы на криволинейном пути
CEE
Элементарной работой dA силы F на
малом перемещении dr называется
скалярное произведение Fdr :
dA Fdr F dt
(1)

12.

Работа силы на криволинейном пути
CEE
Так как скалярное произведение двух векторов
равно произведению их модулей на косинус угла
между ними, то
dA F dr cos α Fds cos α Fs ds
(2)
ds dr
где
— путь точки М за малое время dt; α — угол между
силой и элементарным перемещением (или скоростью ) точки М;
Fs F cos
— проекция силы
называют касательной силой.
F
на направление
dr ,
иногда

13.

Работа силы на криволинейном пути
CEE
Из (2) следует,
что если / 2 , то dA > 0,
если / 2 , то dA < 0
и при / 2 dA = 0.

14.

Работа силы на криволинейном пути
CEE
Работа, совершаемая силой на конечном участке
пути от точки 1 до точки 2 равна сумме
элементарных работ на отдельных бесконечно
малых участках криволинейного пути.
Эта сумма приводится к интегралу :
2
2
2
A12 dA Fds cos α Fs ds
1
1
1
(3)

15.

Работа силы на криволинейном пути
CEE
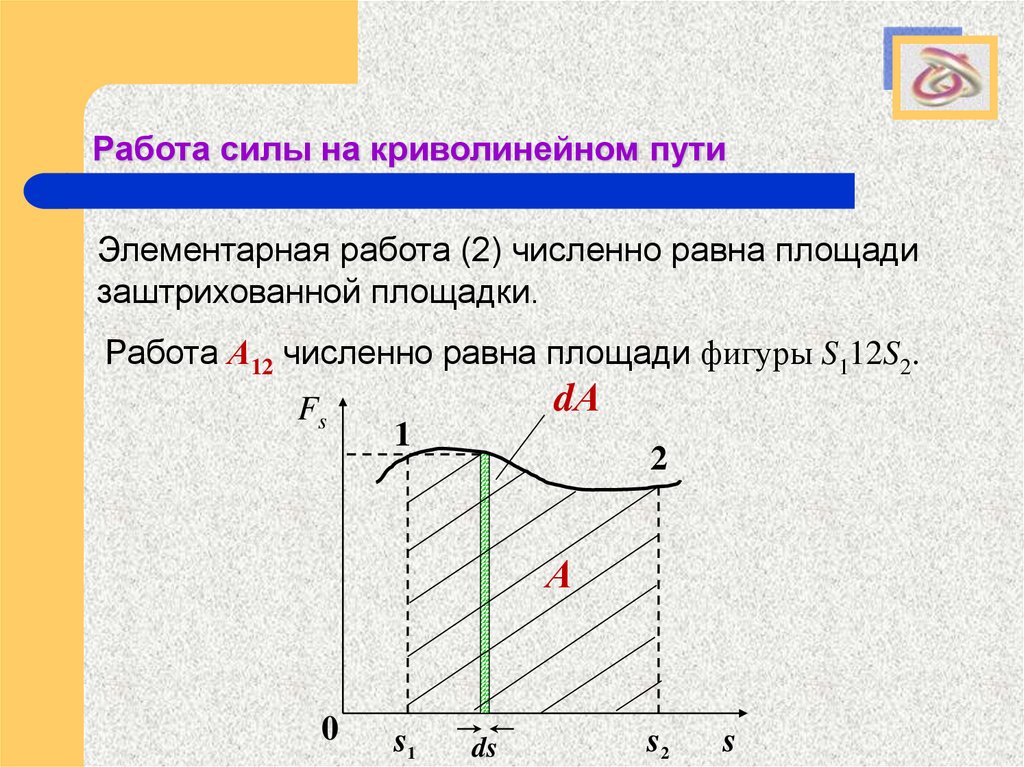
Элементарная работа (2) численно равна площади
заштрихованной площадки.
Работа А12 численно равна площади фигуры S112S2.
Fs
dА
1
2
А
0
s1
ds
s2
s

16.

Мощность
CEE
Работа, совершаемая в
называется мощностью:
единицу
dA dr
N
F
F
dt
dt
времени,
(4)
Единицей мощности в СИ является ватт (Вт) – это такая
мощность, при которой за одну секунду совершается
работа, равная одному джоулю, т. е. 1 Вт = 1 Дж/1с.
1 кВт = 103 Вт, 1 МВт = 106 Вт, 1 ГВт = 109 Вт. В технике
иногда применяется единица мощности, именуемая
лошадиной силой (л. с.) и равная 736 Вт.

17.

Консервативные
и диссипативные силы
CEE
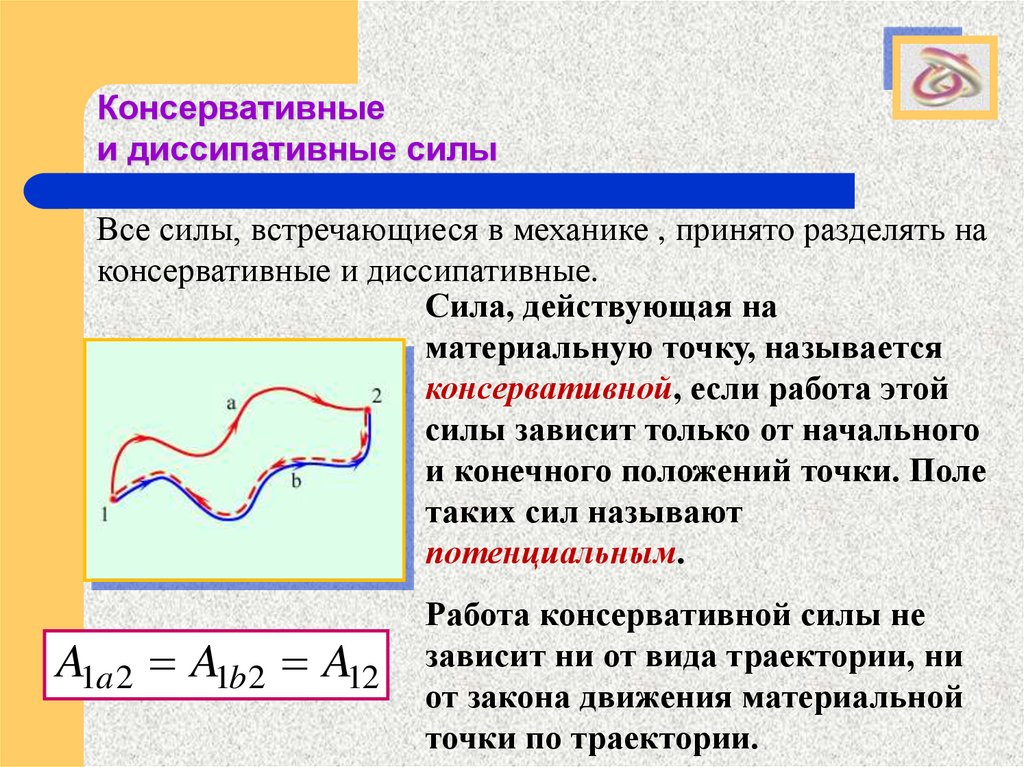
Все силы, встречающиеся в механике , принято разделять на
консервативные и диссипативные.
Сила, действующая на
материальную точку, называется
консервативной, если работа этой
силы зависит только от начального
и конечного положений точки. Поле
таких сил называют
потенциальным.
A1a 2 A1b 2 A12
Работа консервативной силы не
зависит ни от вида траектории, ни
от закона движения материальной
точки по траектории.

18.

Консервативные
и диссипативные силы
CEE
Изменение направления движения точки вдоль
малого участка на противоположное вызывает
изменение знака элементарной работы
dA Fdr
Следовательно,
A2b1 A1b 2
Поэтому работа консервативной силы
замкнутой траектории 1a2b1 равна нулю:
вдоль
A1a 2b1 A1a 2 A2b1 A1a 2 A1b 2 0

19.

Консервативные
и диссипативные силы
CEE
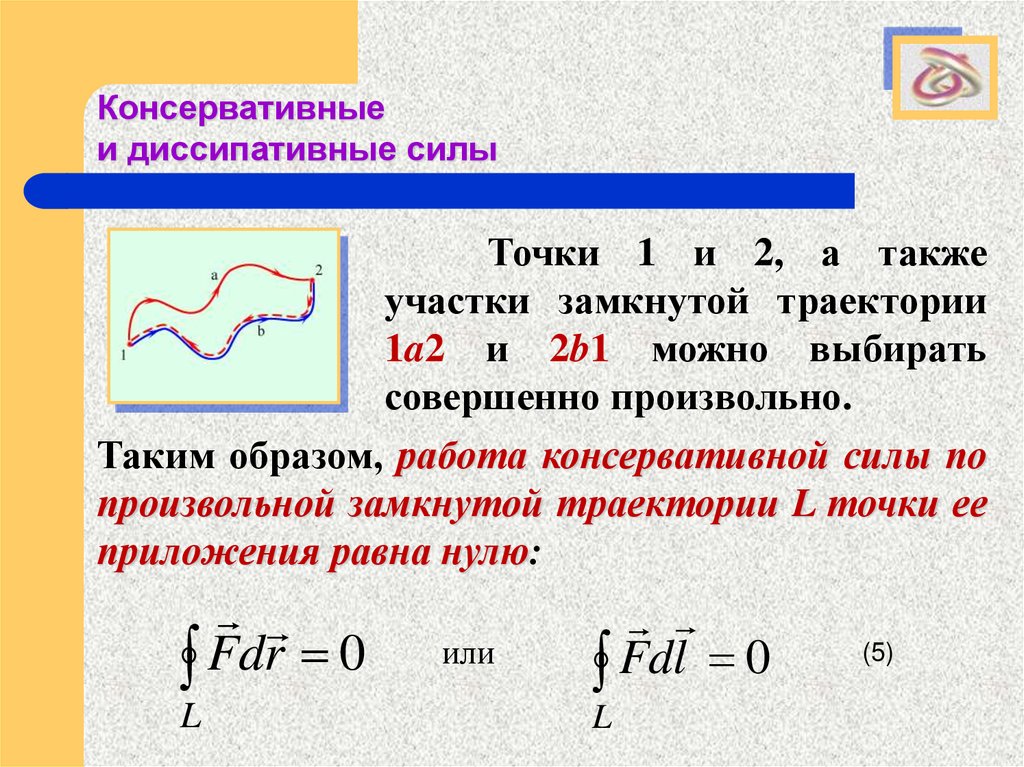
Точки 1 и 2, а также
участки замкнутой траектории
1a2 и 2b1 можно выбирать
совершенно произвольно.
Таким образом, работа консервативной силы по
произвольной замкнутой траектории L точки ее
приложения равна нулю:
Fdr 0
L
или
Fdl 0
L
(5)

20.

Консервативные
и диссипативные силы
CEE
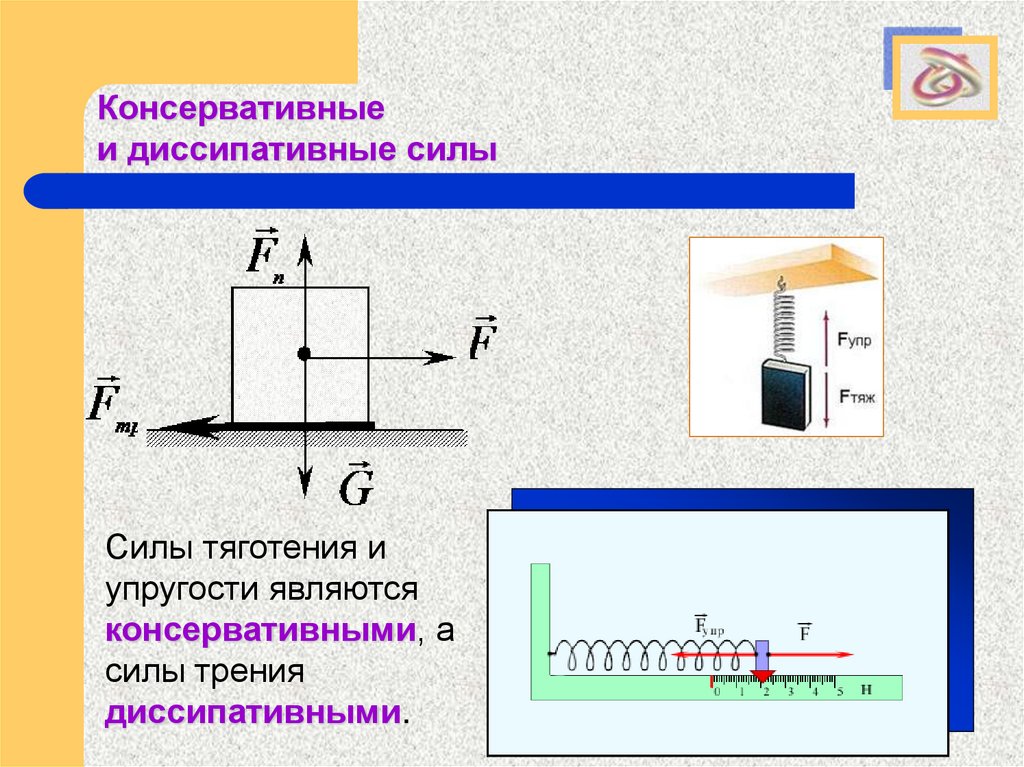
Силы тяготения и
упругости являются
консервативными, а
силы трения
диссипативными.

21.

Потенциальная энергия
CEE
Потенциальная энергия – это энергия,
определяемая взаимным расположением и
характером взаимодействия тел или частей
системы.
Потенциальная энергия системы является
функцией только её координат. Она равна
работе, которую совершают консервативные
силы при переводе тела из данного положения
в положение, выбранное за нулевой уровень
потенциальной энергии.

22.

Потенциальная энергия системы
материальных точек
CEE
Рассмотрим систему, состоящую
многих материальных точек.
из
Если
задано
положение
каждой
материальной
точки,
то
этим
определено и положение всей системы
или ее конфигурация.

23.

Потенциальная энергия системы
материальных точек
CEE
Если силы, действующие на материальные
точки
системы,
зависят
только
от
конфигурации системы то такие силы
называются консервативными.
В этом случае для системы материальных точек
также можно ввести понятие потенциальной
энергии системы:
A12 WП1 WП 2 (WП 2 Wп1 ) Wп
(6)

24.

Потенциальная энергия системы
материальных точек
CEE
где A12 — полная работа консервативных сил,
действующих на материальные точки системы
при переходе ее из положения 1 в положение 2;
WП1 и WП 2 — значения потенциальной энергии
системы в этих положениях.
Из (6) видим, что работа консервативных
сил равна убыли потенциальной энергии.

25.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
F
Пусть под действием консервативной силы
материальная точка совершила перемещение
dr.
При этом потенциальная энергия точки изменилась
dWп
на величину
.
Работа силы равна:
dA Fdr dWп
(7)
С другой стороны:
dA Fdr Fx dx Fy dy Fz dz
(8)

26.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
А
z
dx, dy и dz –
dr
dz
dy
dx
x
О
y
проекции
вектора dr на
оси координат
Х, У и Z
соответственно
Fx, Fy и Fz – проекции вектора силы
на соответствующие оси координат

27.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
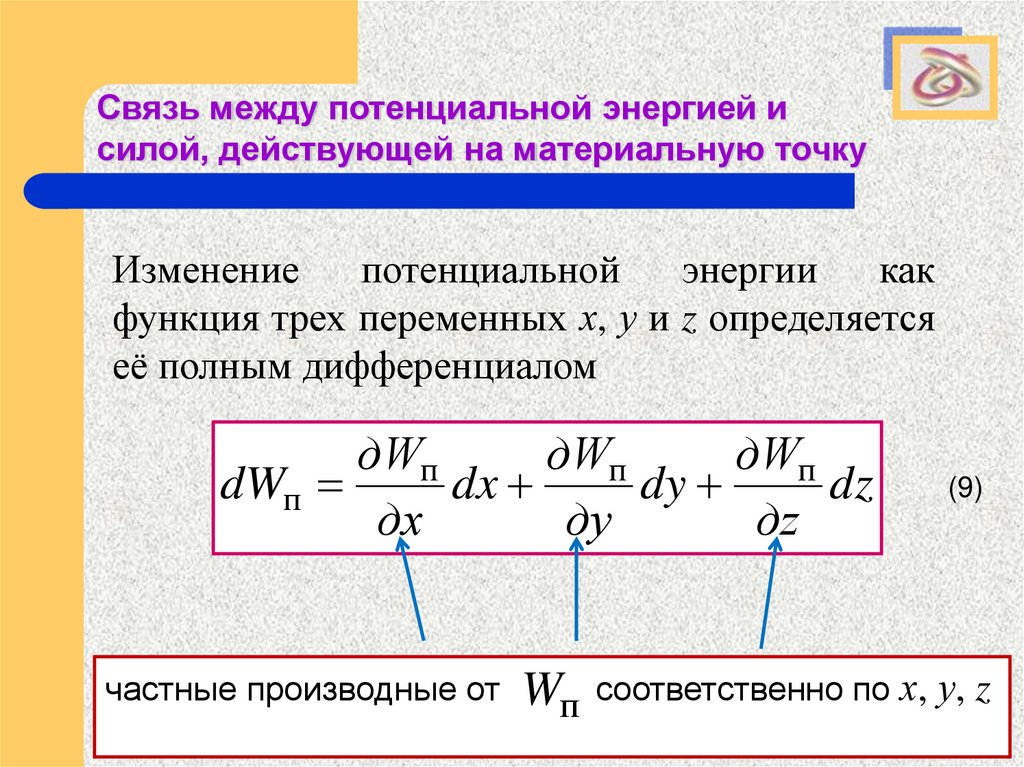
Изменение
потенциальной
энергии
как
функция трех переменных х, у и z определяется
её полным дифференциалом
дWп
дWп
дWп
dWп
dx
dy
dz
дх
дy
дz
частные производные от
Wп
(9)
соответственно по х, у, z

28.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
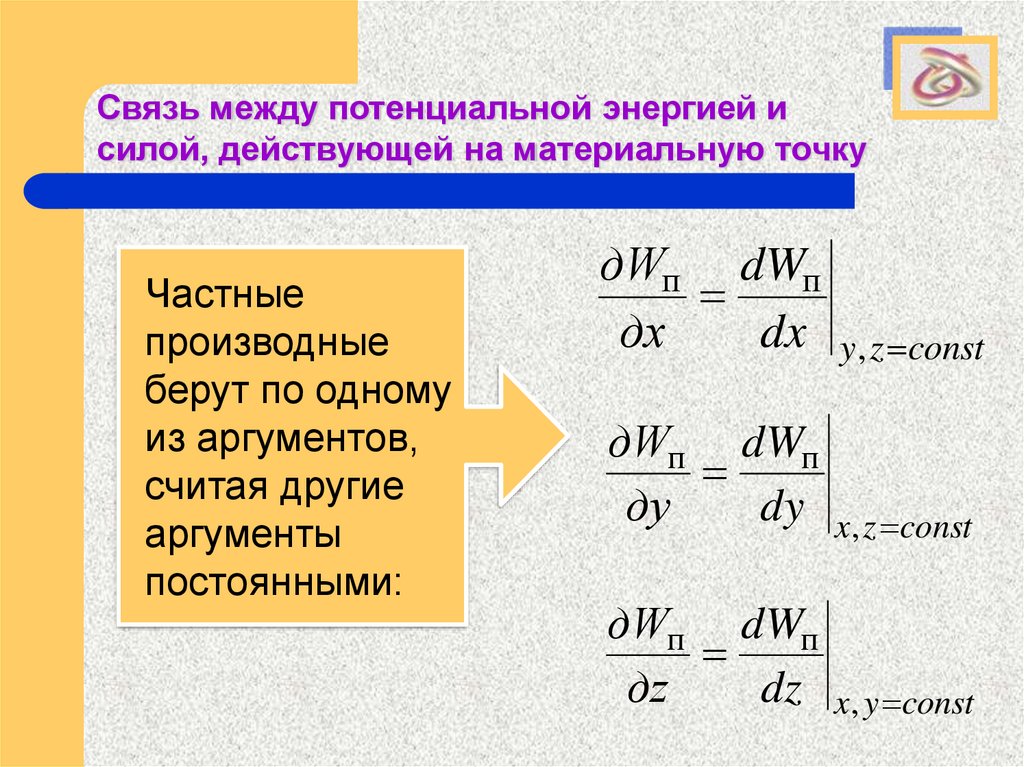
Частные
производные
берут по одному
из аргументов,
считая другие
аргументы
постоянными:
дWп dWп
дx
dx
y , z const
дWп dWп
дy
dy
x , z const
дWп dWп
дz
dz
x , y const

29.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
С учетом (9) выражение (7) перепишем в виде:
дWп
дWп
дWп
dA dWп
dx
dy
dz
дy
дz
дх
(10)
Сравним с (8):
dA Fdr Fx dx Fy dy Fz dz
(8)

30.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
дWп
Fx
дx
Получим:
дWп
Fy
дy
дWп
Fz
дz
(11)

31.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
Как и любой вектор, сила может быть записана
через составляющие (компоненты):
z
k
x
F
i
А
F i Fx j Fy k Fz
(12)
j
y
орты — единичные
векторы, направленные
вдоль осей x, y, z
соответственно.

32.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
Сравнивая (11) и (12), получим:
дWп дWп дWп
F
i
j
k gradWп (13)
дy
дz
дx
где gradWП называется градиентом скалярной
функции WП;
grad
i , j, k
осей.
x
i
y
j
z
k
– единичные векторы координатных

33.

Связь между потенциальной энергией и
силой, действующей на материальную точку
CEE
дWп дWп дWп
F
i
j
k gradWп
дy
дz
дx
(13)
Формула (13) устанавливает дифференциальную
связь между силой, действующей на материальную
точку, и потенциальной энергией системы: вектор
действующей силы равен взятому с
противоположным знаком градиенту
потенциальной энергии.
Из (13) следует, что потенциальная энергия системы
возрастает в направлении, противоположном вектору
консервативной силы.

34.

Потенциальная энергия
упруго деформированного тела
CEE
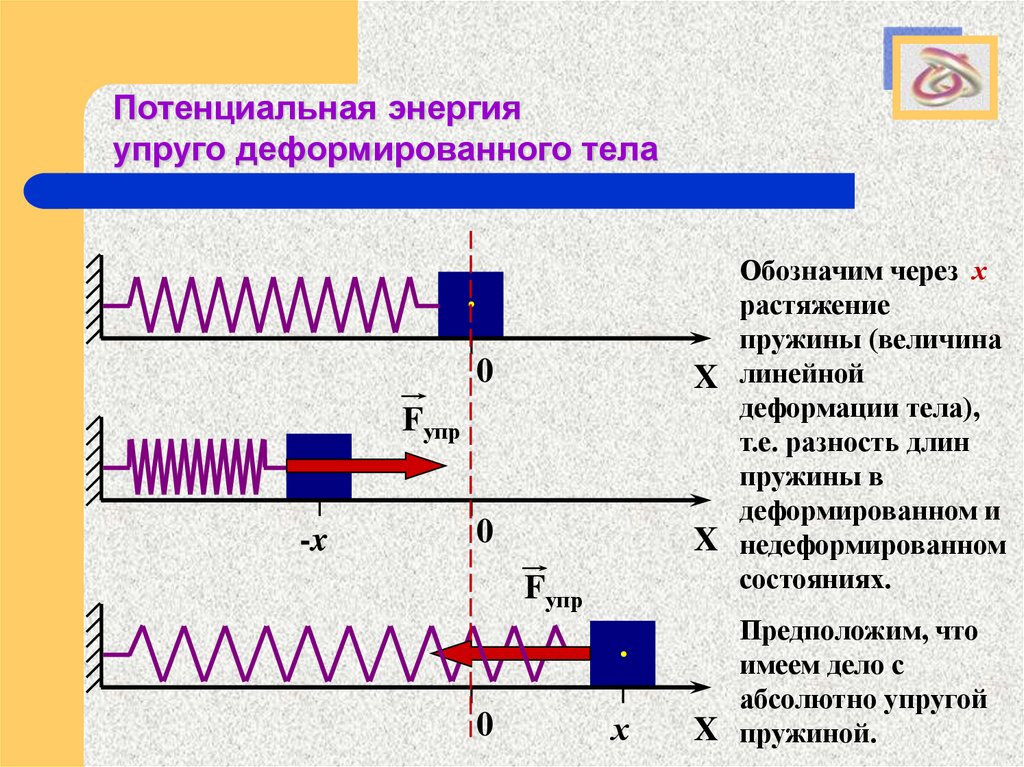
Обозначим через х
растяжение
пружины (величина
X линейной
деформации тела),
т.е. разность длин
пружины в
деформированном и
X недеформированном
состояниях.
0
Fупр
-x
0
Fупр
0
х
Предположим, что
имеем дело с
абсолютно упругой
X пружиной.

35.

Потенциальная энергия
упруго деформированного тела
CEE
В этом случае пружина действует на груз с упругой силой,
пропорциональной смещению
обратную смещению, т. e.:
х
и направленной в сторону
Fупр kxi
k – коэффициент пропорциональности (жесткость пружины).
х – величина линейной деформации тела;
i–
единичный вектор оси Х, вдоль которой происходит
деформация тела.
Знак "минус" означает, что сила упругости противодействует
смещению.

36.

Потенциальная энергия
упруго деформированного тела
CEE
Вычислим работу силы упругости при изменении
величины линейной деформации от x1 до x2 .
Элементарная работа, совершаемая силой
упругости при бесконечно малой деформации,
равна
dA Fупр dх cos Fупрх dх -kxdx

37.

Потенциальная энергия
упруго деформированного тела
CEE
Тогда полная работа силы упругости:
x2
2
x2
2
1
2
2
kx
kx
kx
A kxdx
2 x
2
2
x1
1
(14)

38.

Потенциальная энергия
упруго деформированного тела
CEE
Сравним (14) и (6):
x2
2
x2
2
1
2
2
kx
kx
kx
A kxdx
2 x
2
2
x1
1
(14)
A12 WП1 WП 2 (WП 2 Wп1 ) Wп
(6)
Видим:
kx
Wп
2
2
потенциальная энергия
упруго деформированного
тела

39.

Потенциальная энергия тела
в поле тяготения Земли
CEE
Согласно закону всемирного тяготения
сила притяжения тела к Земле
mM
F =G 2
r
m - масса тела; М – масса Земли;
r – расстояние от центра Земли до тела (длина
радиус вектора, проведённого из центра Земли
к телу);
G - гравитационная постоянная.

40.

Потенциальная энергия тела
в поле тяготения Земли
CEE
Сила тяготения относится к центральным
силам, она направлена к центру Земли, и
изменяется при изменении расстояния r.
Работа силы тяготения
r2
r2
r1
r1
dr
A Fdr GmM 2
r
r2
(15)
mM
mM
1
GmM G
G
r1
r2
r r1

41.

Потенциальная энергия тела
в поле тяготения Земли
CEE
Сравним (15) и (6).
Видим:
mM
Wп G
r
(16)
потенциальная энергия
тела массы т,
находящегося в поле
гравитации Земли,
масса которой М

42.

Потенциальная энергия тела
в поле тяготения Земли
CEE
Изменение потенциальной энергии тела массы
m, поднятого с поверхности Земли (r = R, где R
– радиус Земли) на высоту h (r = R + h),
согласно (16), равно:
1
1
Wп GMm(
)
R h R
GMm(R-(R h)) GMmh
( R h) R
( R h) R
(17)

43.

Потенциальная энергия тела
в поле тяготения Земли
CEE
Если h<<R, то в знаменателе формулы (17)
можно пренебречь слагаемым h и она перейдет
в формулу:
Mmh
Wп G 2 mgh
R
(18)
Потенциальная энергия тела относительно поверхности Земли
где GM / R 2 g – ускорение силы тяжести
на поверхности Земли.

44.

Кинетическая энергия
CEE
Кинетической энергией называют
энергию, зависящую от скорости
движения тела.

45.

Кинетическая энергия
CEE

46.

Кинетическая энергия
CEE
Напишем уравнение движения
материальной точки (частицы) массы m,
движущейся под действием сил,
результирующая которых равна F :
d
m
F
dt

47.

Кинетическая энергия
CEE
Умножим скалярно правую и левую часть
этого
равенства
на элементарное
перемещение точки dr dt
Тогда
d
m dt Fdr
dt
или
<=>
m d Fdr
m d dA

48.

Кинетическая энергия
CEE
Если скорость тела увеличивается от 1 до
то
2
2 2
1
1
m
A12 m d
2
m 2 m 1
A12
2
2
2
или
2
2 ,

49.

Кинетическая энергия
CEE
Обозначим
Тогда
m
WK
2
A12 WK WK
2
1
2
(19)
Работа результирующей всех сил, действующих на
материальную точку, равна изменению
кинетической энергии.

50.

Кинетическая энергия
CEE
Обобщим полученный результат на случай
произвольной системы материальных точек.
Кинетической энергией системы называется
сумма кинетических энергий материальных
точек, из которых эта система состоит или на
которые ее можно мысленно разделить:
mi
WK
2
i 1
n
2
i

51.

Кинетическая энергия
CEE
Напишем соотношение (1) для каждой
материальной точки системы, а затем все
такие соотношения сложим.
В результате снова получим формулу,
аналогичную (1), но для системы
материальных точек.
A12 WK WK
2
1
WK 1 и WK 2 – кинетические энергии системы, а под A12 необходимо
понимать сумму работ всех сил, действующих на материальные точки
системы.

52.

Кинетическая энергия
CEE
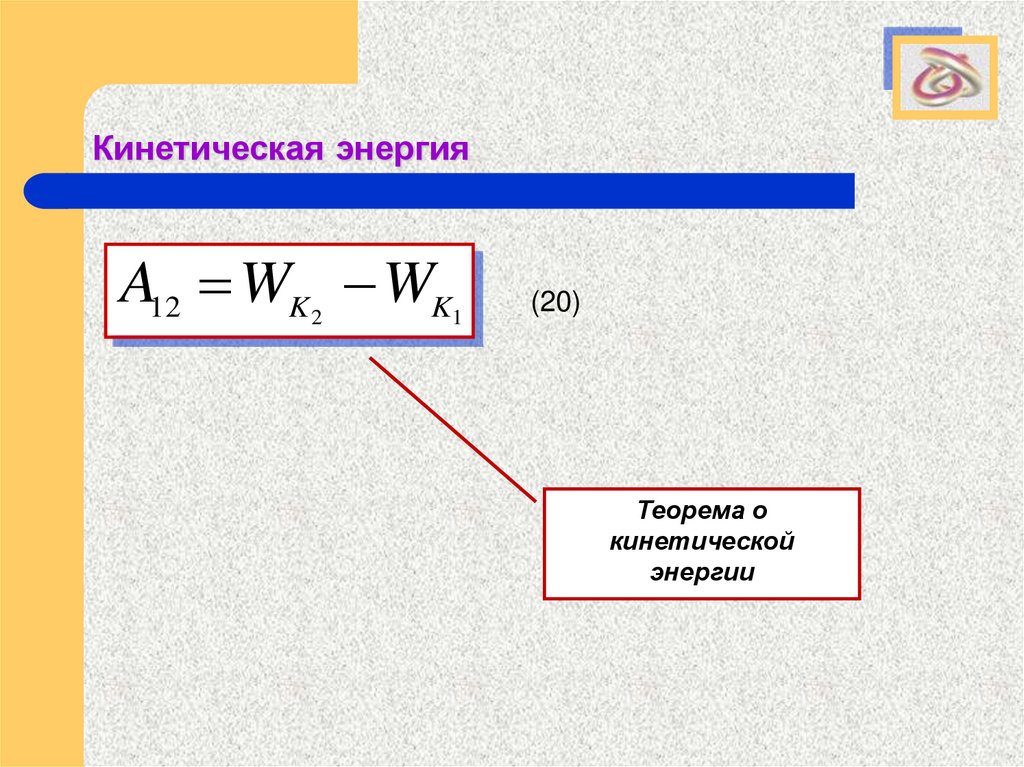
A12 WK WK
2
1
(20)
Теорема о
кинетической
энергии

53.

Закон сохранения энергии в механике
CEE
Изменение кинетической энергии равно
работе сил. Если силы консервативные, то
эта работа равна убыли потенциальной
энергии.
A12 WП WП
1
или
2
A12 (WП WП )
2
1

54.

Закон сохранения энергии в механике
CEE
Следовательно, учитывая (20),:
(WП WП ) WK WK
2
1
2
1
или
WK WП WK WП
1
1
2
(21)
2

55.

Закон сохранения энергии в механике
CEE
Сумма кинетической и потенциальной энергии
представляет собой полную механическую
энергию Е системы:
E WК WП
Тогда, согласно (21):
E WК WП const

56.

Закон сохранения энергии в механике
CEE
Полная механическая энергия
системы материальных точек,
находящихся под действием
консервативных сил остается
постоянной.

57.

Закон сохранения энергии в механике
CEE
В такой системе могут происходить
лишь превращения потенциальной
энергии в кинетическую и обратно,
но полный запас энергии системы
измениться не может.

58.

Общефизический закон сохранения энергии
CEE
Полное количество энергии в
изолированной системе тел и
полей всегда остается
постоянным; энергия лишь может
переходить из одной формы в
другую.

59.

Общефизический закон сохранения энергии
CEE

60.

CEE
Лекцию подготовила к.п.н.
доцент Симдянкина Е.Е.