9. Магнитное поле

1.

Магнитное поле
Лекция № 9

2.

План лекции:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Магнитное поле и его характеристики.
Закон Био Савара Лапласа и его применение к расчету
магнитного поля.
Закон Ампера. Взаимодействие параллельных токов.
Магнитная постоянная. Единицы магнитной индукции и
напряженности магнитного поля.
Циркуляция магнитного поля (закон полного тока) в
вакууме. Теорема Гаусса для магнитного поля.
Работа перемещения проводника с током в постоянном
магнитном поле.
Действие магнитного поля на движущийся заряд.
Движение заряженных частиц в магнитном поле.
Применение магнитного поля.

3.

1. Магнитное поле и его
характеристики
• В 1820 г. датский физик Ханс Эрстед
обнаружил, что магнитная стрелка
поворачивается при пропускании
электрического тока через проводник,
находящийся около нее.

4.

1. Магнитное поле и его
характеристики
• Магнитное поле действует только на
движущиеся в этом поле электрические
заряды.
• При исследовании магнитного поля
используется замкнутый плоский контур с
током (рамка с током), линейные
размеры которого малы по сравнению с
расстоянием до токов, образующих
магнитное поле.

5.

1. Магнитное поле и его
характеристики
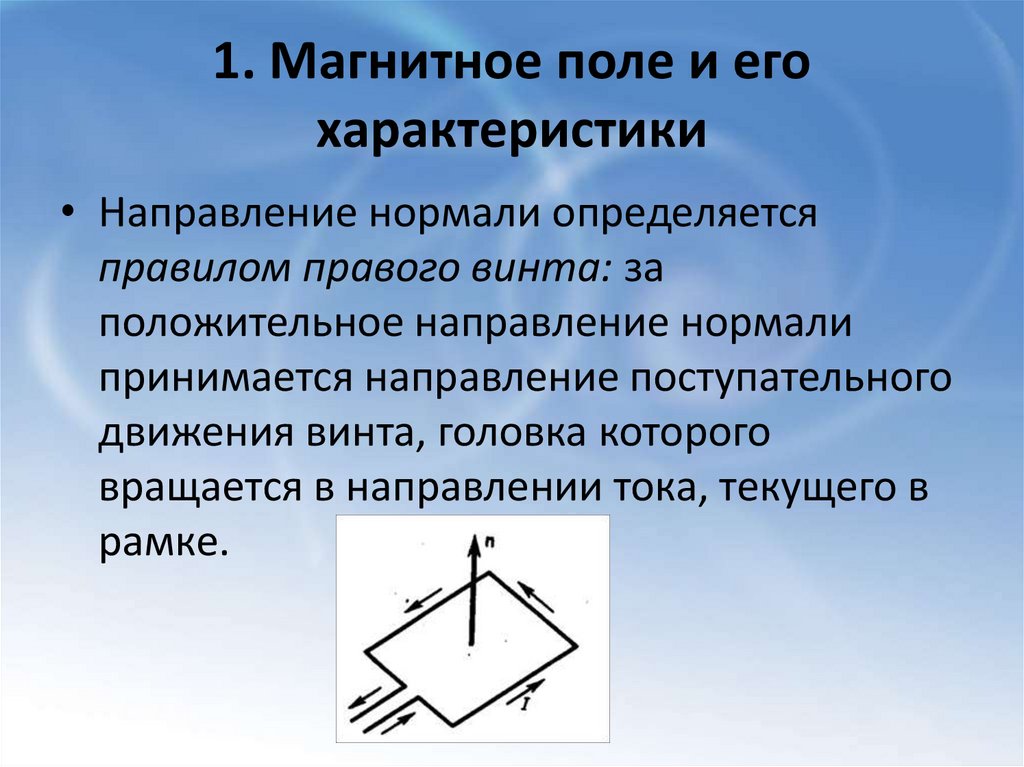
• Направление нормали определяется
правилом правого винта: за
положительное направление нормали
принимается направление поступательного
движения винта, головка которого
вращается в направлении тока, текущего в
рамке.

6.

1. Магнитное поле и его
характеристики
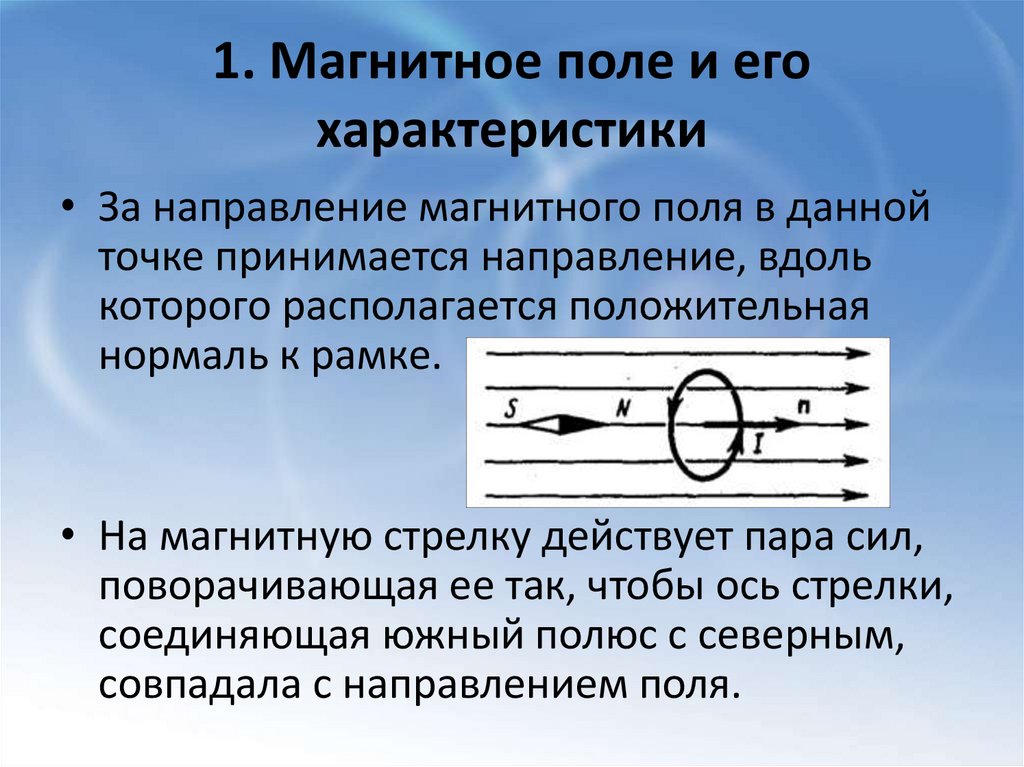
• За направление магнитного поля в данной
точке принимается направление, вдоль
которого располагается положительная
нормаль к рамке.
• На магнитную стрелку действует пара сил,
поворачивающая ее так, чтобы ось стрелки,
соединяющая южный полюс с северным,
совпадала с направлением поля.

7.

1. Магнитное поле и его
характеристики
• Вращающий момент сил:
M pm B
• где pm вектор магнитного момента
рамки с током, В вектор магнитной
индукции.
• Для плоского контура с током I:
pm ISn
• где S площадь поверхности контура
(рамки), n единичный вектор нормали к
поверхности рамки.

8.

1. Магнитное поле и его
характеристики
• Магнитная индукция в данной точке
однородного магнитного поля
определяется максимальным вращающим
моментом, действующим на рамку с
магнитным моментом, равным единице,
когда нормаль к рамке перпендикулярна
направлению поля.
M max
B
pm

9.

1. Магнитное поле и его
характеристики
• Линии магнитной индукции линии,
касательные к которым в каждой точке
совпадают с направлением вектора В.
• Их направление задается правилом правого
винта: головка винта, ввинчиваемого по
направлению тока, вращается в
направлении линий магнитной индукции.

10.

1. Магнитное поле и его
характеристики
• Линии магнитной
индукции поля
кругового тока:
• Линии магнитной
индукции поля
соленоида:
• Соленоид равномерно намотанная на цилиндрическую
поверхность проволочная спираль, по которой течет
электрический ток.

11.

1. Магнитное поле и его
характеристики
Картина магнитного поля

12.

1. Магнитное поле и его
характеристики
• Линии магнитной индукции всегда
замкнуты и охватывают проводники с
током.
• Линии магнитной индукции полосового
магнита; они выходят из северного полюса
и входят в южный.

13.

1. Магнитное поле и его
характеристики
• А. Ампер: в любом теле существуют
микроскопические токи, обусловленные
движением электронов в атомах и молекулах.
• Вектор магнитной индукции В характеризует
результирующее магнитное поле,
создаваемое всеми макро- и микротоками,
т. е. при одном и том же токе и прочих равных
условиях вектор В в различных средах будет
иметь разные значения.

14.

1. Магнитное поле и его
характеристики
• Для однородной изотропной среды
B 0 H
• где 0 магнитная постоянная,
безразмерная величина магнитная
проницаемость среды, показывающая, во
сколько раз магнитное поле макротоков Н
усиливается за счет поля микротоков
среды.

15.

2. Закон Био Савара Лапласа и его
применение к расчету магнитного поля
• Закон Био Савара Лапласа для проводника с
током I, элемент dl которого создает в
некоторой точке А индукцию поля dB,
записывается в виде
0 I dl , r
dB
4
r3
• где dl вектор, по модулю равный длине dl
элемента проводника и совпадающий по
направлению с током, r радиус-вектор,
проведенный из элемента dl проводника в
точку А поля, r модуль радиуса-вектора r.

16.

2. Закон Био Савара Лапласа и его
применение к расчету магнитного поля
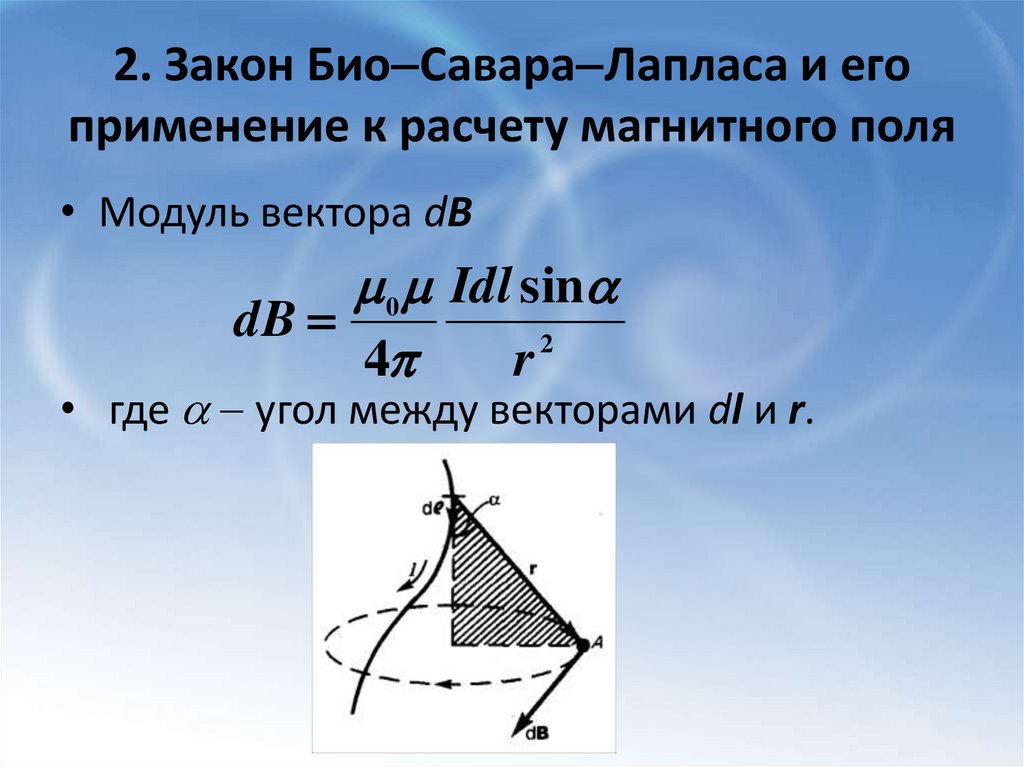
• Модуль вектора dB
0 Idl sin
dB
2
4
r
• где угол между векторами dl и r.

17.

2. Закон Био Савара Лапласа и его
применение к расчету магнитного поля
• Принцип суперпозиции: магнитная
индукция результирующего поля,
создаваемого несколькими токами или
движущимися зарядами, равна векторной
сумме магнитных индукций складываемых
полей, создаваемых каждым током или
движущимся зарядом в отдельности:
n
B Bi
i 1

18.

2. Закон Био Савара Лапласа и его
применение к расчету магнитного поля
1. Магнитное поле прямого тока тока,
текущего по тонкому прямому проводу
бесконечной длины.
R
r
sin
rd
dl
sin
Магнитная индукция, создаваемая
одним элементом проводника:
0 I
dB
sin d
4 R

19.

2. Закон Био Савара Лапласа и его
применение к расчету магнитного поля
• Так как угол для всех элементов прямого
тока изменяется в пределах от 0 до , то:
0 I
0 2 I
B dB
sin d
4 R 0
4 R
• Магнитная индукция поля прямого тока:
0 2 I
B
4 R

20.

2. Закон Био Савара Лапласа и его
применение к расчету магнитного поля
2. Магнитное поле в центре кругового
проводника с током .
Так как все элементы проводника
перпендикулярны
радиусу-вектору (sin 1) и расстояние
всех элементов проводника до центра
кругового тока одинаково и равно R, то:
0 I
dB
dl
2
4 R

21.

2. Закон Био Савара Лапласа и его
применение к расчету магнитного поля
• Тогда
0 I
0 I
I
B dB
dl
2 R 0
2
2
4 R
4 R
2R
• Магнитная индукция поля в центре
кругового проводника с током:
I
B 0
2R

22.

3. Закон Ампера. Взаимодействие
параллельных токов
• Ампер установил, что сила dF, с которой
магнитное поле действует на элемент
проводника dl с током, находящийся в
магнитном поле, равна
dF I dl , B
• где dl вектор, по модулю равный dl и
совпадающий по направлению с током, В
вектор магнитной индукции.

23.

3. Закон Ампера. Взаимодействие
параллельных токов
• Правило левой руки: если ладонь левой
руки расположить так, чтобы в нее входил
вектор В, а четыре вытянутых пальца
расположить по направлению тока в
проводнике, то отогнутый большой палец
покажет направление силы, действующей
на ток.

24.

3. Закон Ампера. Взаимодействие
параллельных токов
• Модуль силы Ампера:
dF IBdl sin
• где угол между векторами dl и В.
• Закон Ампера применяется для
определения силы взаимодействия двух
токов.

25.

3. Закон Ампера. Взаимодействие
параллельных токов
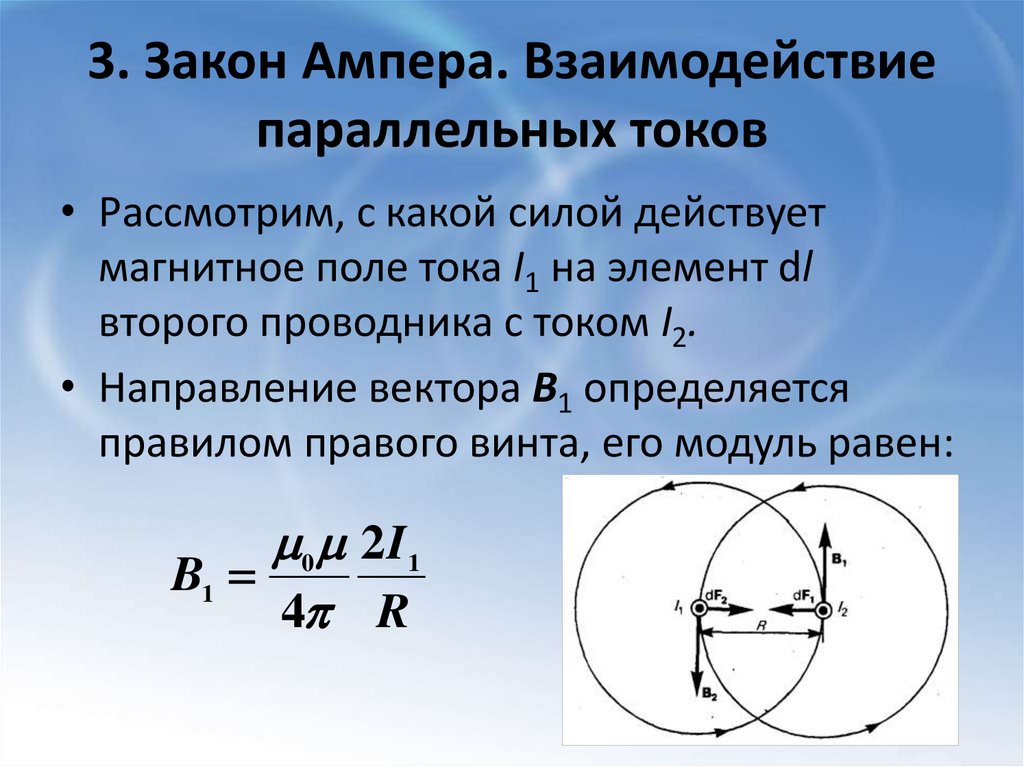
• Рассмотрим, с какой силой действует
магнитное поле тока I1 на элемент dl
второго проводника с током I2.
• Направление вектора B1 определяется
правилом правого винта, его модуль равен:
0 2 I 1
B1
4 R

26.

3. Закон Ампера. Взаимодействие
параллельных токов
• Модуль силы, с учетом того, что угол
между элементами тока I2 и вектором B1
прямой, равен:
dF1 I 2 B1dl
• подставляя значение для В1, получим
0 2 I 1 I 2
dF1
dl
4 R

27.

3. Закон Ампера. Взаимодействие
параллельных токов
• Сила dF2 с которой магнитное поле тока I2
действует на элемент dl первого
проводника с током I1, направлена в
противоположную сторону и по модулю
равна:
0 2 I 1 I 2
dF2 I1 B2dl
dl
4 R
dF1 dF2

28.

3. Закон Ампера. Взаимодействие
параллельных токов
• Два параллельных тока одинакового
направления притягиваются друг к другу
с силой
0 2 I 1 I 2
dF
dl
4 R
• Если токи имеют противоположные
направления, то между ними действует
сила отталкивания, определяемая этой
же формулой.

29.

4. Магнитная постоянная. Единицы
магнитной индукции и напряженности
магнитного поля
• Если два параллельных проводника с током
находятся в вакууме ( 1) то сила
взаимодействия на единицу длины
проводника равна
dF 0 2 I1 I 2
dl 4 R
dF
2 10 7 Н / м
dl
I1 I 2 1 А
R 1м
0 4 10 7 Н / А2 4 10 7 Гн / м

30.

4. Магнитная постоянная. Единицы
магнитной индукции и напряженности
магнитного поля
• Предположим, что элемент проводника dl с
током I перпендикулярен направлению
магнитного поля. Тогда закон Ампера:
dF IBdl
1 dF
B
I dl
• 1 Тл (Тесла) магнитная индукция такого
однородного магнитного поля, которое
действует с силой 1 Н на каждый метр длины
прямолинейного проводника, расположенного
перпендикулярно направлению поля, если по
этому проводнику проходит ток 1 А:
1Тл 1Н /( А м)

31.

4. Магнитная постоянная. Единицы
магнитной индукции и напряженности
магнитного поля
• Так как
0 4 10 7 Н / А2
• в случае вакуума
B 0 H
1
• то
H B / 0
• Единица напряженности магнитного поля
ампер на метр (А/м): 1 А/м
напряженность такого поля, магнитная
индукция которого в вакууме равна 4 10 7 Тл

32.

5. Циркуляция магнитного поля (закон
полного тока) в вакууме. Теорема Гаусса для
магнитного поля
• Теорема о циркуляции для магнитного поля
в вакууме: циркуляция вектора
магнитной индукции поля в вакууме
равна алгебраической сумме токов,
охватываемых этим контуром (т. е.
результирующему току через
поверхность, опирающуюся на контур L),
умноженной на магнитную постоянную:
B dl μ0 I k μ0 j dS
L
k
S

33.

5. Циркуляция магнитного поля (закон
полного тока) в вакууме. Теорема Гаусса для
магнитного поля
• Силовые поля, для которых циркуляция
силового вектора отлична от нуля,
называются вихревыми или
соленоидальными.
• Магнитное поле является вихревым,
а его
силовые линии (линии вектора B )
замкнуты.

34.

5. Циркуляция магнитного поля (закон
полного тока) в вакууме. Теорема Гаусса для
магнитного поля
• Для соленоида:
• для тороида:
B 0 nI
N
B 0
I
2 r
R1 r R2
• где n число витков на единицу длины
соленоида; N полное число витков тороида; r
радиус окружности, лежащей внутри
тороида; R1 и R2 внутренний и наружный
радиусы тороида.

35.

5. Циркуляция магнитного поля (закон
полного тока) в вакууме. Теорема Гаусса для
магнитного поля
• Элементарным потоком магнитной
индукции (магнитным потоком) сквозь
малую поверхность площадью dS
называется физическая величина, равная
dΦm B dS
• Магнитный поток сквозь произвольную
поверхность S
Фm B dS BndS
S
S

36.

5. Циркуляция магнитного поля (закон
полного тока) в вакууме. Теорема Гаусса для
магнитного поля
• Если магнитное поле однородное, а
поверхность S плоская, то
Фm Bn S BS cos Bn
• Единица измерения магнитного потока в СИ
1 Вб (вебер).

37.

5. Циркуляция магнитного поля (закон
полного тока) в вакууме. Теорема Гаусса для
магнитного поля
• Теорема Гаусса для магнитного поля
(силовые линии поля замкнуты):
магнитный поток сквозь произвольную
замкнутую поверхность равен нулю:
B dS 0

38.

6. Работа перемещения проводника с
током в постоянном магнитном поле
• Элементарная работа, совершаемая силой
Ампера при малом перемещении в
магнитном поле элемента тока:
δA FA dr Idl , B dr I dr , dl B IdS B I d m
A IdФm
• где dФm магнитный поток сквозь
поверхность, которую описывает
проводник при его малом перемещении.

39.

6. Работа перемещения проводника с
током в постоянном магнитном поле
• Работа сил Ампера при перемещении в
магнитном поле замкнутого контура с
постоянным током I:
A12 I IN Фm
• где Ψ – изменение потокосцепления
контура при перемещении; N количество
витков контура; Фm магнитный поток
через поверхность контура.

40.

7. Действие магнитного поля на
движущийся заряд
• Сила, действующая на электрический заряд Q,
движущийся в магнитном поле со скоростью υ,
называется силой Лоренца:
F Q B
• Направление силы Лоренца определяется с помощью
правила левой руки: если ладонь левой руки
расположить так, чтобы в нее входил вектор В, а четыре
вытянутых пальца направить вдоль вектора υ, то
отогнутый большой палец покажет направление силы,
действующей на положительный заряд.

41.

7. Действие магнитного поля на
движущийся заряд
• Модуль силы Лоренца:
F Q B sin
• Магнитное поле не действует на
покоящийся электрический заряд.
• Магнитное поле действует только на
движущиеся в нем заряды.

42.

7. Действие магнитного поля на
движущийся заряд
• Если на движущийся электрический заряд
помимо магнитного поля с индукцией В
действует и электрическое поле с
напряженностью Е, то результирующая сила
F, приложенная к заряду, равна векторной
сумме сил:
F QE Q B

43.

8. Движение заряженных частиц в
магнитном поле
• Будем считать, что магнитное поле
однородно и на частицы электрические
поля не действуют:
• 1. если заряженная частица движется в
магнитном поле со скоростью вдоль
линий магнитной индукции, то магнитное
поле на частицу не действует и она
движется равномерно и прямолинейно.

44.

9. Применение магнитного поля
Магнит

45.

9. Применение магнитного поля
• Магнитное поле Земли.

46.

9. Применение магнитного поля
• Магнитное поле Земли защищает планету
от космических лучей и солнечного ветра.