Приложение: частица в "потенциальной яме" ("ящике") конечной глубины

1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц

10 (2). Приложение: частица в
"потенциальной яме" ("ящике") конечной
глубины.

2. Одномерная прямоугольная потенциальная яма ("ящик")

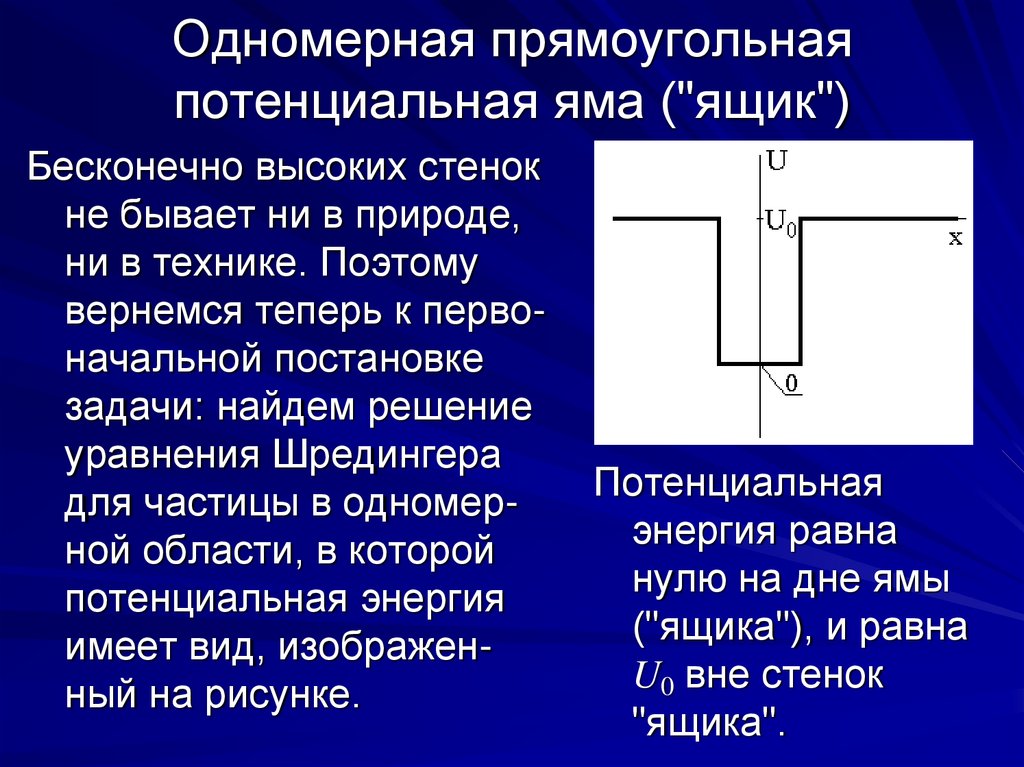
Одномерная прямоугольная
потенциальная яма ("ящик")
Бесконечно высоких стенок
не бывает ни в природе,
ни в технике. Поэтому
вернемся теперь к первоначальной постановке
задачи: найдем решение
уравнения Шредингера
для частицы в одномерной области, в которой
потенциальная энергия
имеет вид, изображенный на рисунке.
Потенциальная
энергия равна
нулю на дне ямы
("ящика"), и равна
U0 вне стенок
"ящика".

3.

Докажем прежде всего одно важное свойство собственных функций: собственные функции, принадлежащие различным собственным значениям, ортогональны, т.е., если m ≠ n, то:
x x dx
m
n
0
Доказательство: если m ≠ n, то интеграл
nx mx
An Am sin
sin
dx
L
L
1
x
x
An Am cos (m n) cos (m n) dx 0
2
L
L
0
L
равен нулю.

4.

Если m = n, то интеграл не равен 0, и из условия нормировки можно найти коэффициент An:
l
1 2
2 nx
2
2
2 nx
dx 1 A sin
n
n
L
dx
1 2
An L 1
2
An 1 cos
dx
2 0
L
An
2
L
т.е. нормирующий множитель у всех собственных функций одинаков. Поэтому
2
nx
n
sin
(10.8)
L
L

5.

Для поля, изображенного на рисунке, все пространство можно
разделить на 3 области I, II, III:
x a
U 0 ,
(10.9)
U x 0,
a x a
U ,
x a
0
причем E < U0.
Как и раньше, требуется решить
одномерное стационарное
уравнение Шредингера
2m
2
( E U ) 0
(9.6)

6.

Подставляя в уравнение Шредингера условие (10.9), получаем для областей I и III
одинаковые уравнения:
2
d 2m
(10.10)
2 (U 0 E ) 0
2
dx
а для области II (внутри ямы потенциальная
энергия U = 0): 2
d 2m
2 E 0
(10.11)
2
dx
Обозначим для краткости
1
1
k
2mE ; k1
2m(U 0 E )

7.

Тогда уравнение (10.10) принимает вид:
(10.12)
d 2
2
dx
2
k1 E 0
а уравнение (10.11):
d 2
2
k
E 0
2
dx
(10.13)
Для области II общее решение уравнения
(10.13), как уже говорилось, известно и имеет вид:
II ( x ) A sin kx B cos kx
где A и B - неизвестные пока константы.
Общее решение уравнения (10.12) также известно и имеет вид: Ce k x De k x
где C и D - также неизвестные пока константы.
1
1

8.

Учтем условие, согласно которому волновая функция не должна обращаться в бесконечность (условие ограниченности). Слева от ямы (в области I)
координата x < 0, и уходит в . Справа от ямы (в
области III) координата x > 0, и уходит в .
Поэтому в области I должна равняться нулю константа D, а в области III должна обратиться в нуль
константа C. Таким образом, волновые функции в
первой, второй и третьей областях имеют вид:
I x Ce
k1 x
II ( x) A sin kx B cos kx
III x De
k1 x
(10.14)

9.

Итак, мы получили решения уравнения Шредингера
для каждой из трех областей. Теперь эти решения
надо "сшить" на границах областей так, чтобы были непрерывны сами функции , и их первые производные по x. Для левой границы x = -a условие
непрерывности функции имеет вид:
Ce k1a A sin ka B cos ka
(10.15)
а условие непрерывности производной:
k1a
(10.16)
Ck1e Ak cos ka Bk sin ka
Аналогично для правой границы x = a:
De
k1a
A sin ka B cos ka
Dk1e k1a Ak cos ka Bk sin ka
(10.17)
(10.18)

10.

Таким образом, получены 4 уравнения относительно 4 неизвестных A, B, C, D. Решить эту систему
можно различными способами. Например, умножим уравнение (10.15) на k1 и вычтем его из уравнения (10.16), исключая, таким образом, константу С:
A( k cos ka k1 sin ka ) B(k sin ka k1 cos ka ) 0
(10.19)
Аналогично, умножив уравнение (10.17) на k1 и складывая его с (10.18), исключаем константу D:
A( k1 sin ka k cos ka ) B(k1 cos ka k sin ka ) 0
(10.20)

11.

Получили систему из 2-х однородных линейных
уравнений для двух неизвестных A и B. Условием
существования нетривиального решения такой
системы является равенство нулю ее определителя:
( k cos ka k1 sin ka ) ( k1 cos ka k sin ka )
( k sin ka k1 cos ka ) (k1 sin ka k cos ka ) 0
Раскрывая скобки и выполняя простые тождественные преобразования, получаем уравнение:
k k1 tgka k1 k tgka 0
откуда получаем два корня:
k11 = k tgka
и
k12 = -k ctgka.
(10.21)
(10.22)

12.

Подставляя первый корень (10.21) в уравнение
(10.19), получаем: A = 0. Далее, из уравнений
(10.15) - (10.18) находим D = C, и соотношение между константами B и C:
C
k a
B
cos ka
e
11
Далее, запишем условие нормировки:
a
2 k11a a
e
2
2 k11 x
2 k11 x
2
C e dx
cos kxdx e
dx
2
cos ka a
a
C e
2
2 k11a
1
a
sin 2ka
1
2
2
k11 cos ka 2k cos ka
(10.23)
и найдем из него константу C:
e2 ka tgka
k sin 2ka e 2 ka tgka
C
1
a
sin 2ka 2 1 ka tgka
k tgka cos2 ka 2k cos2 ka
2
(10.24)

13.

Итак, волновые функции для 1-го корня имеют вид
I Ce
III Ce
k1 x
II ( x) Ce
k1 x
k1 x
(10.25)
cos kx
cos ka
где константа C определяется формулой (10.24). Отметим, что первый корень приводит к четным волновым функциям, т.е. (x) = (-x).
Далее, выполняя аналогичные вычисления со вторым корнем, получаем B = 0, D = -C, и соотношение
между константами A и C:
C k1a
A
e
sin ka

14.

Из условия нормировки получаем формулу для
константы C, совпадающую с формулой (10.24).
Таким образом, волновые функции для 2-го
корня имеют вид: Таким образом, волновые
функции для 2-го корня имеют вид:
I Ce k1x
II ( x ) Ce
III Ce k1x
k1 x
sin kx
sin ka
(10.26)
где константа C, как и для 1-го корня, определяется формулой (10.24). Отметим, что второй корень приводит к нечетным волновым функциям,
т.е. (x) = - (-x).

15.

Теперь надо сделать самое главное: определить
спектр уровней энергии частицы в потенциальной
яме. Для этого надо в формулы (10.21) и (10.22)
вместо k и k1 подставить их значения:
k
k1
1
1
2mE
2m(U 0 E )
(10.27)
(10.28)
Сначала займемся уравнением (10.21). Подставляя
в него (10.27) и (10.28), получаем трансцендентное уравнение относительно энергии E:
2m
2
2m
2m
E tg
E a
(U 0 E )
2
2

16.

В "докомпьютерные" времена такие уравнения решали графически следующим образом. Обозначим:
ka, k1a
Умножая обе части уравнения (10.21) на a, получаем в новых обозначениях:
tg
Далее найдем сумму квадратов величин и :
a k k
2
2
2
2
2
1
2m
2m
2mU 0a
a 2 E 2 U 0 E
2
2
2
(10.29)

17.

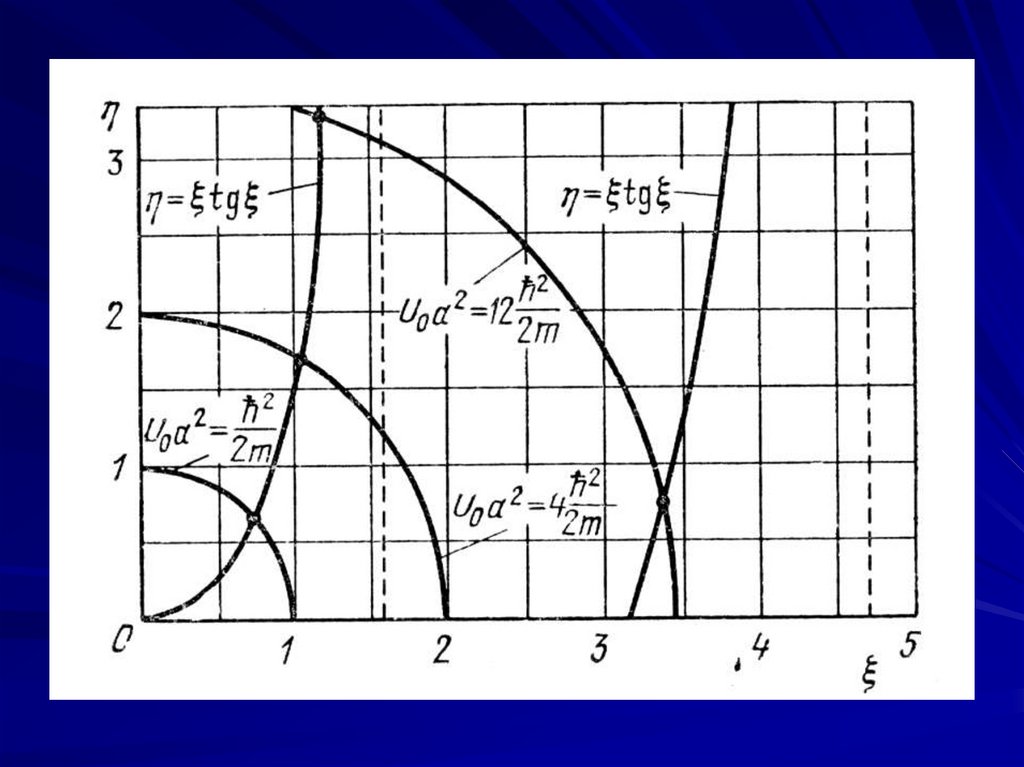
Это уравнение окружности в
координатах и с радиусом
a
2mU 0
Искомые уровни энергии можно определить, найдя точки пересечения кривой tg с окружностью указанного радиуса (см. рисунок). На рисунке приведены
окружности для трех значений параметра глубины
ямы U0a2. Первым двум значениям соответствуют
по одной точке пересечения в первом квадранте (
и - положительные числа), а третьему - две точки
пересечения.

18.

19.

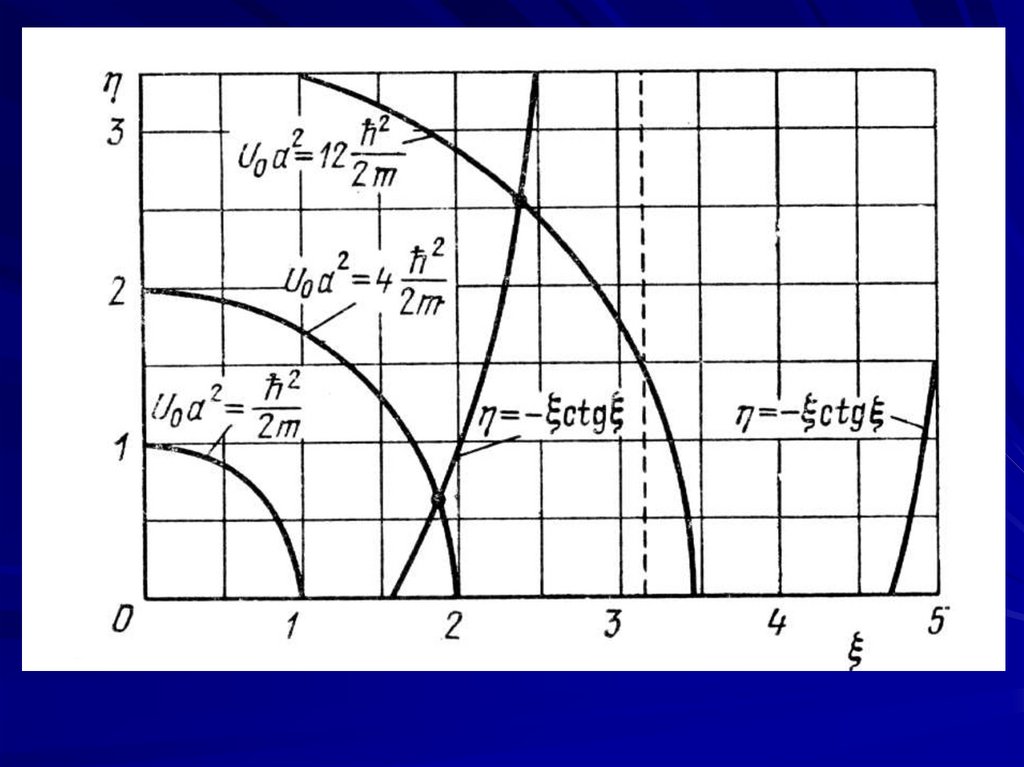
Выполняя аналогичные преобразования для формулы
(10.22), получим ctg
Соответствующие значения
энергии получим, найдя точки
пересечения этой кривой с окружностью (10.29) (см.
рисунок). Как видно из рисунка, для параметра глубины ямы U 0a 2 2 / 2m пересечение отсутствует, а
для следующих двух параметров глубины имеется
по одному пересечению. Итак, для трех последовательных значений параметра глубины U0a2 получаем соответственно один, два и три уровня энергии.

20.

21.

В настоящее время подобные уравнения
решают численными методами, причем
решения получают за долю секунды и с
гораздо более высокой точностью. На
всех современных языках программирования имеются готовые подпрограммы
для решения таких уравнений. Однако
графический метод имеет преимущество в наглядности.

22.

В пределе при U0 → полученные результаты
должны совпадать с формулами, найденными
выше для ямы с бесконечно высокими стенками.
Проверим это. Запишем формулу (10.21) в виде:
k1
U0 E
tgka
k
E
При U0 → правая часть этой формулы также
стремится к бесконечности. Это означает, что в
пределе ka n / 2 где n - целое нечетное число.
Подставляя сюда вместо k его значение из форму2 2
лы (10.27), получаем
2
En n
2ma
что для нечетных чисел n совпадает с формулой
(10.6).

23.

Аналогично, записывая формулу (10.22) в виде
k1
U0 E
ctgka
k
E
видим, что в пределе при U0 → правая часть этой
формулы стремится к - . Отсюда
ka n / 2
где n - целое четное число.
Подставляя значение k из формулы (10.27), получаем
2 2
En n
2
2ma
что также совпадает с формулой (10.6) для четных
чисел n.