Похожие презентации:
Решение показательных уравнений
1.
Алгебра и начала анализа11 класс.
2. Цель урока
• Выработатьумения решать
показательные уравнения
• Сформировать
навыки решения
показательных уравнений
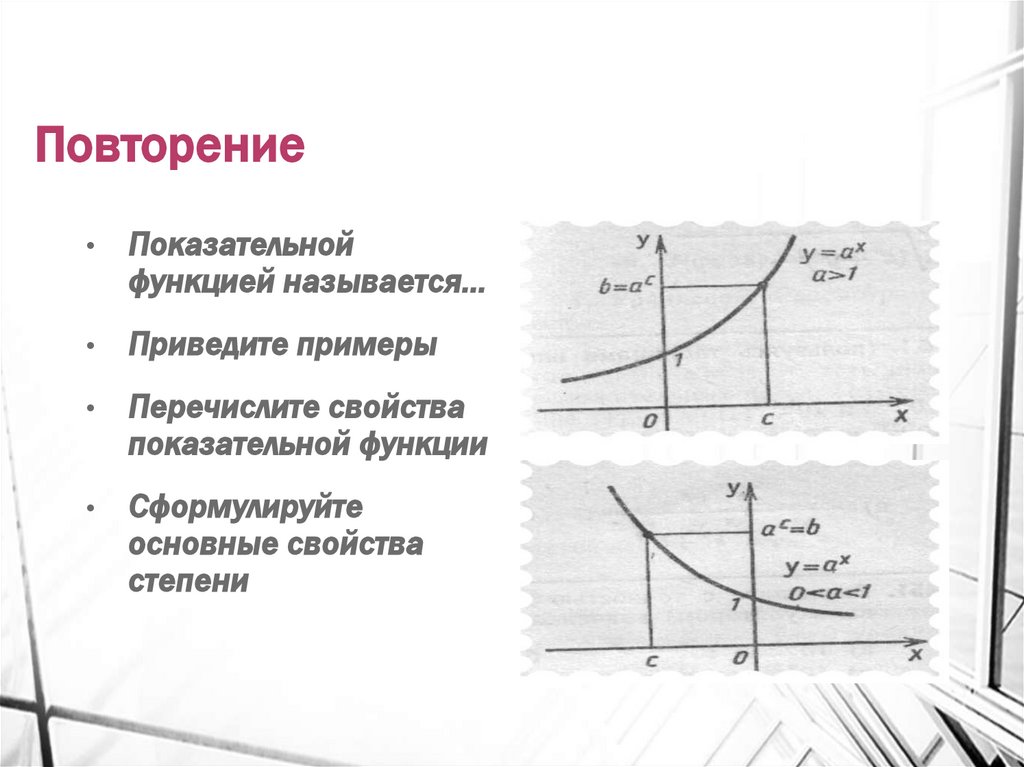
3. Повторение
Показательной
функцией называется…
Приведите примеры
Перечислите свойства
показательной функции
Сформулируйте
основные свойства
степени
4. Проверь себя
• Функцияу а, где а>0, х R,
х
называется показательной
функцией.
Например:
у 2
х
1
у
2
х
у (0,3)
х
5. Основные свойства функции
у аПри а>1
Область определения функции- множество
действительных чисел:
Множество значений функции- множество
положительных действительных чисел:
Функция возрастает на всей области
х
D( a x ) R
Е (а х ) R
х2 x1 , a
ее определения:
x2
a
x1
если
При х=0
а 1
х
х ;0 , то0 а х 1;
х 0; , то
ах 1
6. При 0<а<1
При 0<а<1Область определения функции- множество
действительных чисел:
Множество значений функции- множество
положительных действительных чисел:
Функция убывает на всей области ее
определения:
D( a x ) R
Е (а ) R
х
х2 x1 , a x2 a x1
если
При х=0
а 1
х
х ;0 , то
а х 1;
х 0; , то0 а х 1
7. Свойства степени
а а ах
у
х у
х
а
х у
а
у
а
х
х
х
а в а в
а
х
у
а
х у
8. Показательное уравнение
Показательным называется уравнение,содержащее переменную в показателе
степени.
Например:
2 4
х
3 2 3
х
х 2
63
х 1 3
2 5 0,1 (10 )
х
х
9. Методы решения показательных уравнений
1.Приведение показательного уравнения к
виду
f х
х
а
а
2.
Вынесение общего множителя за скобки.
3.
Приведение показательного уравнения к
квадратному.
4.
Графическое решение показательного
уравнения.
10. 1. Приведение показательного уравнения к виду
f хх
а
а
Решить уравнение:
Образец 1
27 1 х
3
3
1 х
1
81
3 4
3 3 3 х 3 4
3 3 х 4
3 х 7
7
х
3
7
Ответ :
3
11.
Образец 2х2
4 5 х
х2
5 х 4
7
2
2
7
7
7
2
2
х2 5х 4
х2 5х 4 0
х1 1, х2 4
Ответ: 1; 4.
12.
Образец 3х
2 5 0,1 10
х
2 5
х
10 10
10 10
х
1
3 х 4
х 3х 4
х 2
Ответ : 2.
х 1 3
3 х 3
13.
Замечание:а
а
Наприме
р:
2
2
f х
1
f х
а
х 5
1
х 5
2
0
х 5 0
х 5
0
14. 2. Вынесение общего множителя за скобки.
Решите уравнение:Образец 1
3 х 2 3 х 2 63
3 х 2 3 2 2 63
3 х 2 7 63
3 х 2 9
3 х 2 32
х 2 2
х 4
Ответ : 4
15.
Образец 24 3 х 2 5 3 х 1 6 3 х 5
3 х 4 3 2 5 31 6 5
3 х 36 15 6 5
3 х 45 5
1
3
9
3 х 3 2
х
х 2
Ответ : 2
16. 3. Приведение показательного уравнения к квадратному.
Решить уравнение:Образец 1
вернёмся
4х 3 2х 4
4 2
х
2 х
22 х
к
замене
22 х 3 2 х 4
2х 4
обозначим
2 х 22
2х t
х1 2
t 2 3t 4 0
2 х 1( решения
t1 4
нет)
t2 1
Ответ : 2.
17.
Пример:4х + 2х+1 – 24 = 0
Решение:
Заметив , что 4х=(22 )х=( 2х)2 и
2х+1 = 2х × 21 , запишем уравнение в виде:
(2х )2 + 2×2х – 24 = 0,
Введем новую переменную 2х = у;
Тогда уравнение примет вид:
У2 + 2у – 24 = 0
D = в2 – 4 а с = 22 – 4×1×(–24) = 100> 0
, находим у1 = 4, у2 = – 6.
Получаем два уравнения:
2 х= 4
22 = 2 2
х = 2.
и
2х = – 6
корней нет.
18.
Образец 222 х 22 х 15
2
2
22 2 х х 15
2
4
4 2 х х 15
2
обозначим
2х 4
2 х 22
х1 2
2х t
4
15
t
4t 2 15t 4 0
4t
t1 4
t2
1
4
1
2 х ( решения
4
нет )
Ответ : х 2
19. 4. Графическое решение показательных уравнений
Решить уравнение:2 х
х
Строим графики
функций
их
у 2
.
у х
Графики функций не
имеют общих точек.
Ответ: решений нет
20.
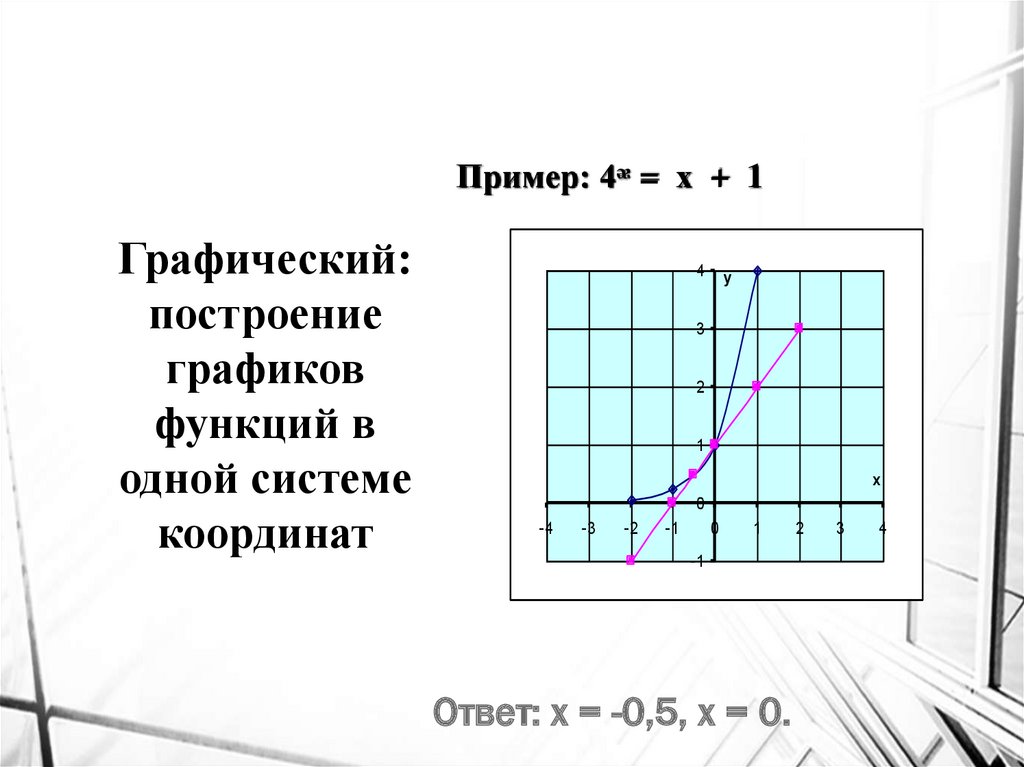
Пример: 4ᵆ = х + 1Графический:
построение
графиков
функций в
одной системе
координат
4
у
3
2
1
х
0
-4
-3
-2
-1
0
1
-1
Ответ: х = -0,5, х = 0.
2
3
4
21. Закрепление. Реши самостоятельно
Решить уравнение:2 х
1
1)9
27
2)36 2163 х 1 1
х
3)17
х 2 5 х 6
1
4)5 х 1 5 х 5 х 1 31
5)3х 2 3х 810
1 х
1
6) 7 х 6
7
7)9 х 8 3х 9
8)22 х 1 7 2 х 4
1
9)5 х
5
10)2 х 3
х 1
4
22. Проверь ответы, поставь себе оценку
9-10 - «5»
7-8 - «4»
5-6 - «3»
4 и менее – «2»
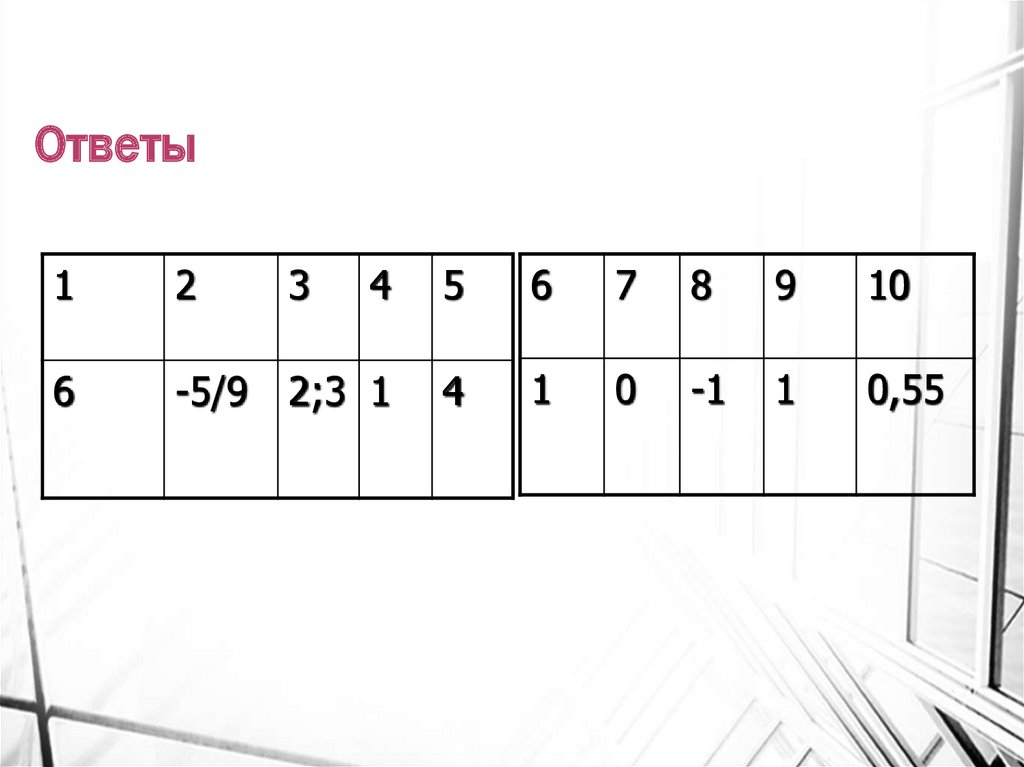
23. Ответы
12
3
4
5
6
7
8
9
10
6
-5/9
2;3 1
4
1
0
-1
1
0,55
24. 2) Решите уравнение:
32x 3
3 x 1
3
x 2
625
600
x 7
25.
Решение.5 x 15
2
3 x 1
3
4 x 8
5
3 x 21
2
x 7
3
2 x 14
5
,
так
600 23 3 52
3 x 1
2
x 7
3
2 x 14
5
0
обе части уравнения на данное
Разделим
выражение и получим :
2 x 6
2 x 6
3
2 x 6
5
2
1
(2 3 5)
30 30
2 x 6
2 x 6
0
2x 6 0
x 3
Ответ : x 3
1
как
26. Основные результаты урока
Повторили определение и свойства показательнойфункции
Познакомились с методами решения показательных
уравнений
Научились подбирать способы решения для
конкретных заданий
27. Домашнее задание
§12 выучить, № 208-214(1,3)- решитьДополнительно- решить уравнения:
1) 2
х 2 1
2)3
2 х 1
5
х 2 1
0,001 10
8 3 3
х
3)2 х 2 х 2 3
1 2
4)3 х
3
х
х 3 2




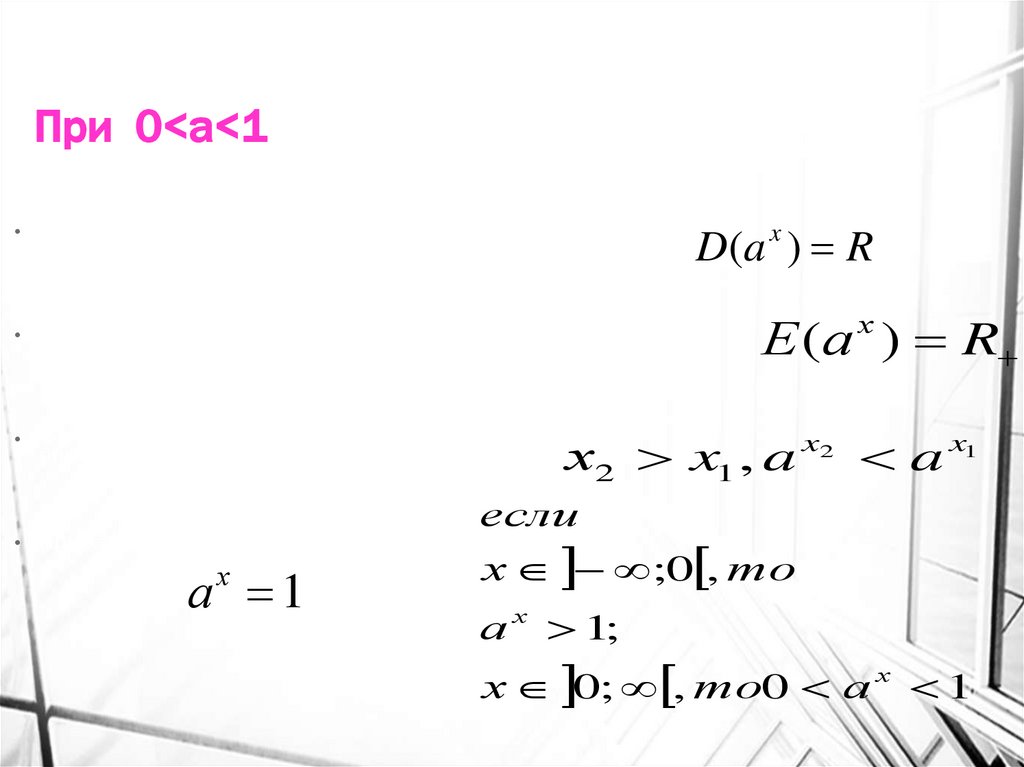



















 Математика
Математика








