Вычитание векторов. Умножение вектора на число

1. Вычитание векторов. Умножение вектора на число.

2. Вычитание

Разностью векторов a и b называется такой
вектор, сумма которого с вектором b равна
вектору a .

3. Вычитание

Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C

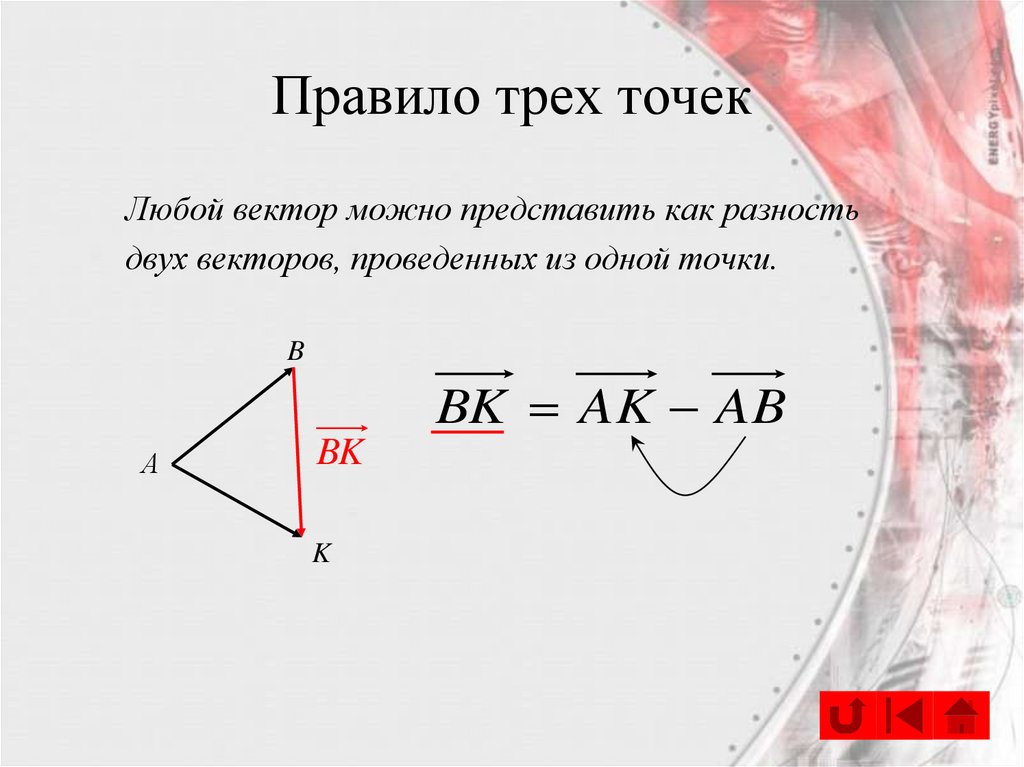
4. Правило трех точек

Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
BK AK AB
А
BK
K

5. Сложение с противоположным

Разность векторов
как сумму вектора
a
a
и
b можно представить
и вектора,
противоположного вектору
b.
a b a b
a
B
b
a b
b
O
А
a

6. Умножение вектора на число

Произведением ненулевог о вектора a на число k
называется такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

7. Свойства

• Произведением нулевого вектора на любое число
считается нулевой вектор.
0 n 0
• Произведение любого вектора на число нуль есть
нулевой вектор.
n 0 0

8. Свойства

Для любыхвект оровa и b и любых
чисел k, l справедливы равенст ва:
(kl)a k(la ) сочет ат ельный закон
k( aPL
b ) PK
k a k b 1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон

9. Признак коллинеарности

Если существует такое число k при котором
выполняется равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы.

10. Повторение

а) CM MK CK
б) DM MA DA
в) SD ST TD
г) PL PK KL
д) AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK