Типовые динамические звенья

1.

ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ
Алгоритмические звенья, которые описываются обыкновенными
дифференциальными уравнениями первого и второго порядка,
получили название типовых динамических звеньев.
• Безынерционное звено (усилительное);
• Апериодическое звено;
• Колебательное звено;
• Идеальное дифференцирующее звено;
• Реальное дифференцирующее звено;
• Идеальное интегрирующее звено;
• Реальное интегрирующее звено;
• Форсирующее звено;
• Звено чистого запаздывания

2.

ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ
1) Безынерционное звено (усилительное)
Безынерционное звено является простейшим среди
всех типовых звеньев.
Оно передает сигнал с входа на выход мгновенно, без
искажений его формы. В звене может происходить только
усиление или ослабление мгновенных значений входной
величины.
Математическое описание звена
Передаточная функция
y t kx t .
W(s) = K

3.

Переходная характеристика
Амплитудно-фазовая характеристика
W j K ,
Im[W(i )]
K
Re[W(i )]
Амплитудно-частотная характеристика
Импульсная характеристика
A( )
K
w(t) = L-1[W(s)] = K·δ(t)
0
Фазо-частотная характеристика

4.

Логарифмическая амплитудно-частотная характеристика
L 20 lg A 20 lg K
Сигналы любой частоты (от нуля до бесконечности)
проходят через безынерционное звено с одинаковым
отношением амплитуд выходной и входной величин,
равным K.
Безынерционное звено не создает фазовых сдвигов между
входной и выходной величиной.

5.

Примерами таких пропорциональных звеньев могут служить,
рычажный механизм, жесткая механическая передача, редуктор,
электронный усилитель сигналов на низких частотах, делитель
напряжения и др.
U1 = (R1 + R2)·I
U2 = R2·I
U2 = [R2/(R1 + R2)]·U1
K = R2/(R1 + R2) у(t) = K·х(t)

6.

2) Апериодическое звено 1-го порядка (инерционное)
Математическое описание звена
T·dу(t)/dt + у(t) = K·х(t)
Передаточная функция
где K – коэффициент усиления;
T – постоянная времени, характеризующая инерционность
системы, т.е. продолжительность переходного процесса в ней.
Поскольку постоянная времени характеризует некоторый
временной интервал, то ее величина должна быть всегда
положительной, т.е. (T > 0).

7.

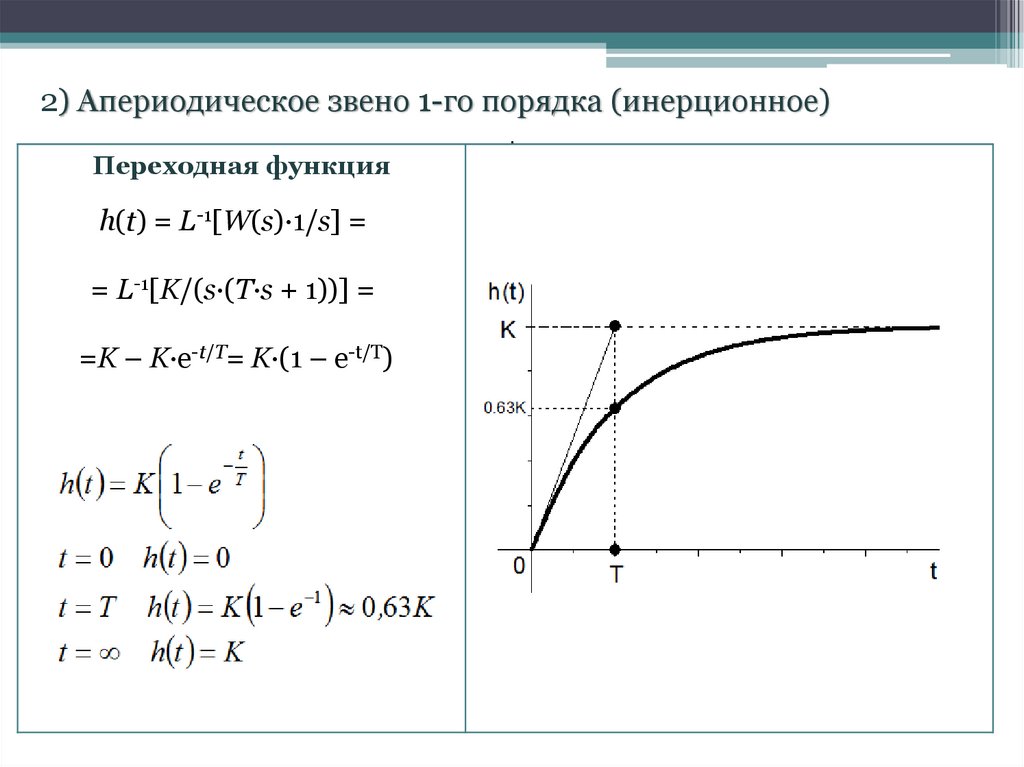
2) Апериодическое звено 1-го порядка (инерционное)
.
Переходная функция
h(t) = L-1[W(s)·1/s] =
= L-1[K/(s·(T·s + 1))] =
=K – K·e-t/T= K·(1 – e-t/T)

8.

Весовая функция
.

9.

2) Апериодическое звено 1-го порядка (инерционное)
АФЧХ
(Амплитудная фазочастотная
характеристика)
.

10.

2) Апериодическое звено 1-го порядка (инерционное)
АЧХ
ФЧХ
.

11.

2) Апериодическое звено 1-го порядка (инерционное)
Чем больше частота входного сигнала, тем больше отставание по
фазе выходной величины от входной. Максимально возможное
отставание равно 900. При частоте с=1/Т сдвиг фаз равен –450.
Гармонические сигналы малой частоты ( < с) пропускаются
звеном хорошо – с отношением амплитуд выходной и входной
величин, близким к передаточному коэффициенту K. Сигналы
большой частоты ( > с) плохо пропускаются звеном
Чем больше постоянная времени Т, т.е. чем больше инерционность,
тем меньше АЧХ вытянута вдоль оси частот, или, тем уже полоса
пропускания частот.
Инерционное звено первого порядка по своим частотным свойствам
является фильтром низкой частоты.

12.

ЛАЧХ
.

13.

Примерами апериодического звена I-ого порядка могут служить:
электрический RC-фильтр, термоэлектрический преобразователь,
резервуар с сжатым газом и т.п.

14.

3) Интегрирующее звено
Математическое описание звена
В интегральной форме это уравнение имеет вид:
Передаточная функция
где K – коэффициент усиления;
T – постоянная времени (время интегрирования);
T = 1/K.

15.

3) Интегрирующее звено
Переходная характеристика
Амплитудно-фазовая характеристика
Амплитудно-частотная характеристика
Импульсная характеристика
Фазо-частотная характеристика

16.

Логарифмическая амплитудно-частотная характеристика
Интегрирующее
звено
ослабляет
высокие
частоты
и
неограниченно
(теоретически) усиливает низкие частоты.
Фазовый сдвиг постоянен и равен –
900.
Примерами интегрирующего звена являются операционный усилитель в
режиме интегрирования, интегрирующим звеном является также обычный
гидравлический демпфер.

17.

4) Реальное интегрирующее звено
Математическое описание звена
Передаточная функция
где k – коэффициент усиления;
T – постоянная времени, характеризующая инерционность
системы, т.е. продолжительность переходного процесса в ней.
Реальное
интегрирующее
звено
представляет
собой
последовательное соединение идеального интегрирующего звена и
апериодического.

18.

4) Реальное интегрирующее звено
Переходная функция
Весовая функция

19.

4) Реальное интегрирующее звеное
.
АФЧХ

20.

4) Реальное интегрирующее звено
АЧХ
ФЧХ
Из характеристик видно, что
звено также пропускает сигналы
тем сильнее, чем меньше их
частота.
.

21.

4) Реальное интегрирующее звено
.
ЛАЧХ
L, дБ
a
30
L( )
-20
20
b
y,0
-180
10
y( )
0
10
, Гц
100
-40
-90
y1( )
y2( )
c
0
= 1/T
, Гц
Из характеристики
видно,
что
звено
приближается
к
идеальному интегрирующему звену при
частотах,
меньших
сопрягающей частоты,
тем
точнее,
чем
меньше
рабочая
частота по сравнению с
сопрягающей.

22.

5) Колебательное звено
Математическое описание звена
d 2 y t
dy t
T
2T
y t kx t
2
dt
dt
2
где k – коэффициент усиления;
T – постоянная времени, характеризующая инерционность
системы, т.е. продолжительность переходного процесса в ней.
- коэффициент демпфирования звена (или коэффициент
затухания).
В зависимости от величины коэффициента демпфирования
различают четыре типа звеньев:
а) колебательное 0< <1;
б) консервативное звено =0;
в) апериодическое звено II порядка >1;
г) неустойчивое колебательное звено <0.

23.

Передаточная функция:

24.

Переходная функция

25.

Весовая функция

26.

Частотные характеристики колебательного звена
АФЧХ
АФХ для консервативного звена
W j
k
T 2 j
2
k
2 2
1 1 T
.
Для апериодического звена 2-го
порядка
1
T1T2

27.

АЧХ
Максимум (резонансный пик)
имеет амплитуду
.

28.

ФЧХ:
.

29.

ЛАЧХ:
.
Асимптотическая ЛАЧХ
колебательного звена:
Область низких частот:
T << 1; т.е. << 1/T; можно
пренебречь
выражением
T2 2.
Получаем: L( ) = 20lgK.
Это горизонтальная прямая.
Область высоких частот:
T >> 1; т.е. >> 1/T;
можно пренебречь 1 в сравнении с
выражением T2 2.
Получаем L( ) = 20lgK – 40lg(T ).
Это – уравнение прямой с
наклоном -40 дб/декаду.
Асимптотическую ЛАЧХ может
быть получена при =1

30.

ЛАЧХ
.
В районе сопрягающей частоты ωс = 1/T имеется максимум (так
называемый "горб"), из-за чего поведение асимптотической ЛАХ в
этой области может существенно отличаться от истинной.
Это явление называется резонансом.

31.

6) Идеальное дифференцирующее звено
Математическое описание звена
dx1
x2 k
dt
В операторной форме это уравнение имеет вид:
x2 k p x1
Передаточная функция
где K – коэффициент усиления;
W(s) = K·s

32.

6) Идеальное дифференцирующее звено
Переходная функция
h(t)
.
Амплитудно-фазовая
характеристика
Амплитудно-частотная
характеристика
k t
Фазо-частотная характеристика
0
t, c
Весовая функция
w(t) = K '(t)
( ) 90 o
Логарифмическая амплитудночастотная характеристика
L( ) 20 lg K 20 lg

33.

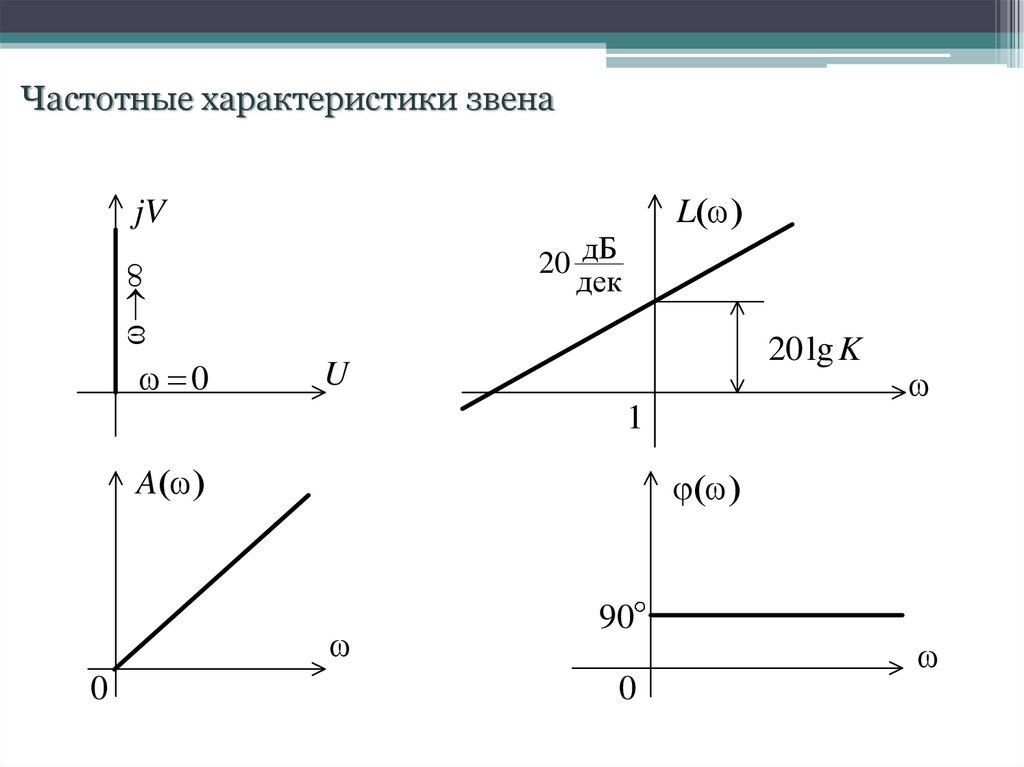
Частотные характеристики звена
jV
L
®∞
20 дБ
дек
0
20 lg K
U
1
A
0
90
0

34.

6) Идеальное дифференцирующее звено
Из характеристик видно, что звено пропускает сигнал тем сильнее,
чем выше его частота. Это свойство является в автоматических
системах часто нежелательным, так как звено может в значительной
степени повышать уровень действующих в системе помех, которые,
как правило, являются высокочастотными.
Единственным идеальным дифференцирующим звеном является
тахогенератор постоянного тока, если в качестве входной величины
рассматривать угол поворота его ротора, а в качестве выходной –
напряжение якоря U.
Приближенно в качестве идеального дифференцирующего звена
может рассматриваться операционный усилитель в режиме
дифференцирования

35.

7) Реальное дифференцирующее звено
Дифференциальное уравнением в операторной форме
Передаточная функция
где K – коэффициент усиления;
Т- постоянная времени
Звено условно можно представить в
виде
двух
включенных
последовательно
звеньев
–
идеального
дифференцирующего
звена и апериодического звена
первого порядка.

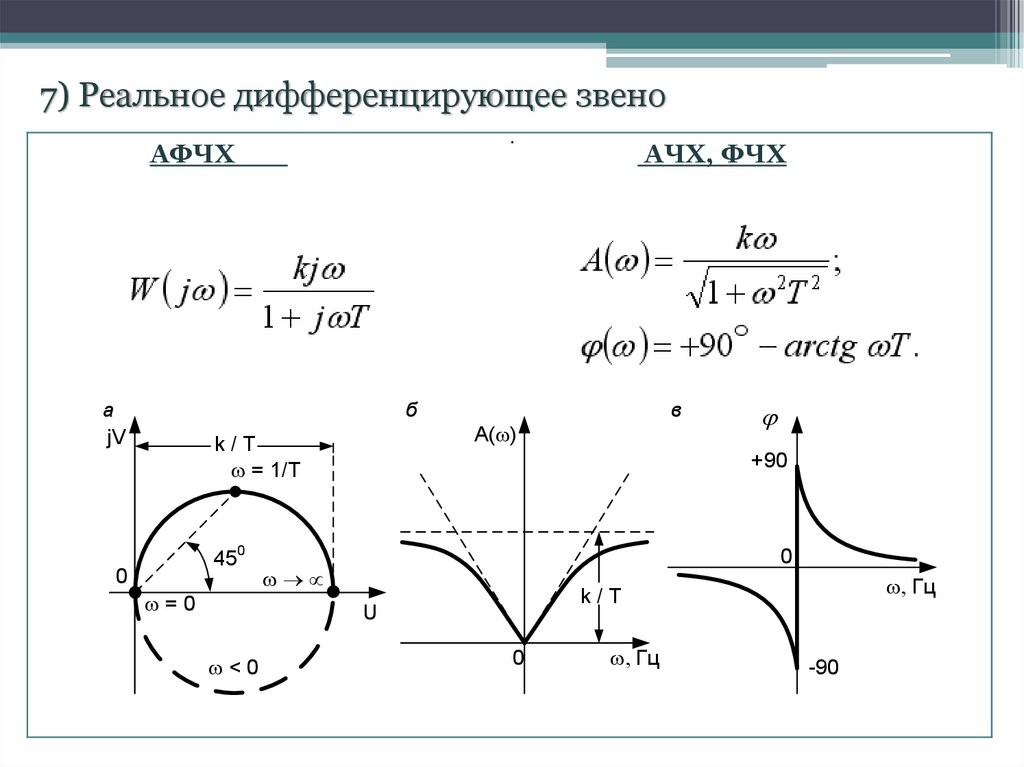
36.

7) Реальное дифференцирующее звено
Переходная функция
.
Функция веса

37.

7) Реальное дифференцирующее звено
.
АФЧХ
а
jV
АЧХ, ФЧХ
б
A( )
k/T
= 1/T
450
0
=0
в
+90
0
®µ
, Гц
k/T
U
<0
0
, Гц
-90

38.

7) Реальное дифференцирующее звено
Амплитудная характеристика реального звена отличается от
амплитудной характеристики идеального дифференцирующего
звена (показана пунктиром). Характеристики совпадают в
области низких частот. В области высоких частот реальное звено
пропускает сигнал хуже, чем идеальное звено.
На
высоких
частотах
фазовый
сдвиг
постепенно
уменьшается, стремясь в пределе к нулю при → 0.
Реальное звено ведет себя подобно идеальному только в
области низких частот.
ЛАЧХ

39.

7) Реальное дифференцирующее звено
.
Примеры реальных дифференцирующих звеньев:
дифференцирующие RC-цепь, RL-цепь и дифференцирующий
трансформатор.
a
U1
С
б
R
U2
U1
в
R
L
U2
U1
L, R
U2
M

40.

8) Звено чистого запаздывания
Звеном чистого запаздывания называется такое звено,
выходная величина которого полностью повторяет входную
величину, но со сдвигом во времени на величину (время
запаздывания).
Динамика процесса описывается уравнением:
y t x t
Передаточная функция
где - длительность запаздывания.

41.

8) Звено чистого запаздывания
Переходная функция
АФЧХ
.
Функция веса
ФЧХ
АЧХ
ЛАЧХ

42.

8) Звено чистого запаздывания
.