Похожие презентации:
Автоматика. Типовые звенья САУ и их свойства
1. АВТОМАТИКА (2015-16)
Кафедра информационных системи технологий (ИСиТ)
Бейтюк Ю.Р.
заведующий кафедрой ИСиТ
к.т.н., доцент
1
2. Лекция 7-8. Типовые звенья САУ и их свойства Типовые звенья САУ
Для анализа САУ используют метод декомпозиции. Для этогосистема автоматического управления разбивается на динамические
звенья.
Звеном направленного действия называется звено,
которое передает воздействие только в одном направлении - с
"выхода" одного звена на "вход" другого, так, что изменение
состояния первого звена не влияет на состояние предшествующего
звена, работающего на его вход.
В результате при разбиении системы на звенья
направленного действия, математическое описание каждого такого
звена может быть составлено без учета его связей с другими
звеньями.
Звенья систем регулирования могут иметь разную
физическую основу (электрические, пневматические, механические и
др. звенья), но относится к одной группе. Соотношения входных и
выходных сигналов в звеньях одной группы описываются
2
одинаковыми передаточными функциями.
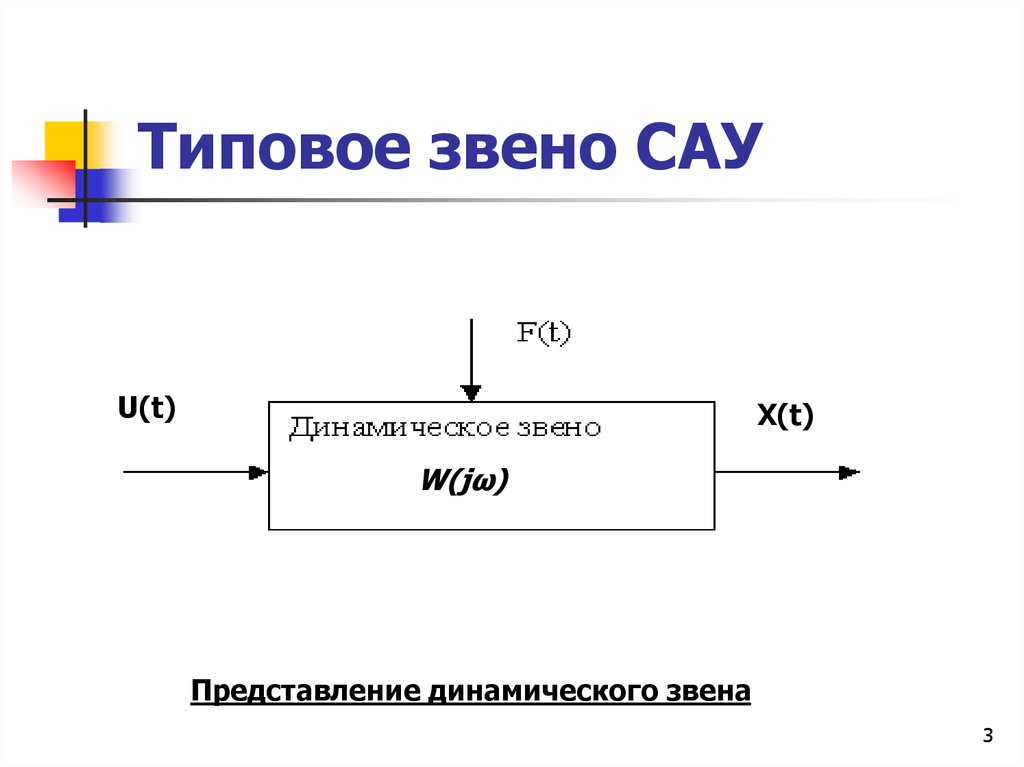
3. Типовое звено САУ
U(t)X(t)
W(jω)
Представление динамического звена
3
4. Типовые звенья САУ
Простейшими типовыми звеньями являются:апериодическое
колебательное
интегрирующее
усилительное (безинерционное)
дифференцирующее
запаздывающее
Они описываются дифференциальными
уравнениями не выше второго порядка.
4
5. Апериодическое звено
Уравнение движения дляапериодического звена имеет вид:
dX
T
X kU
dt
Т – постоянная времени звена
К – передаточный коэффициент
Х – выходная регулируемая величина
U – входное (управляющее) воздействие
t - время
5
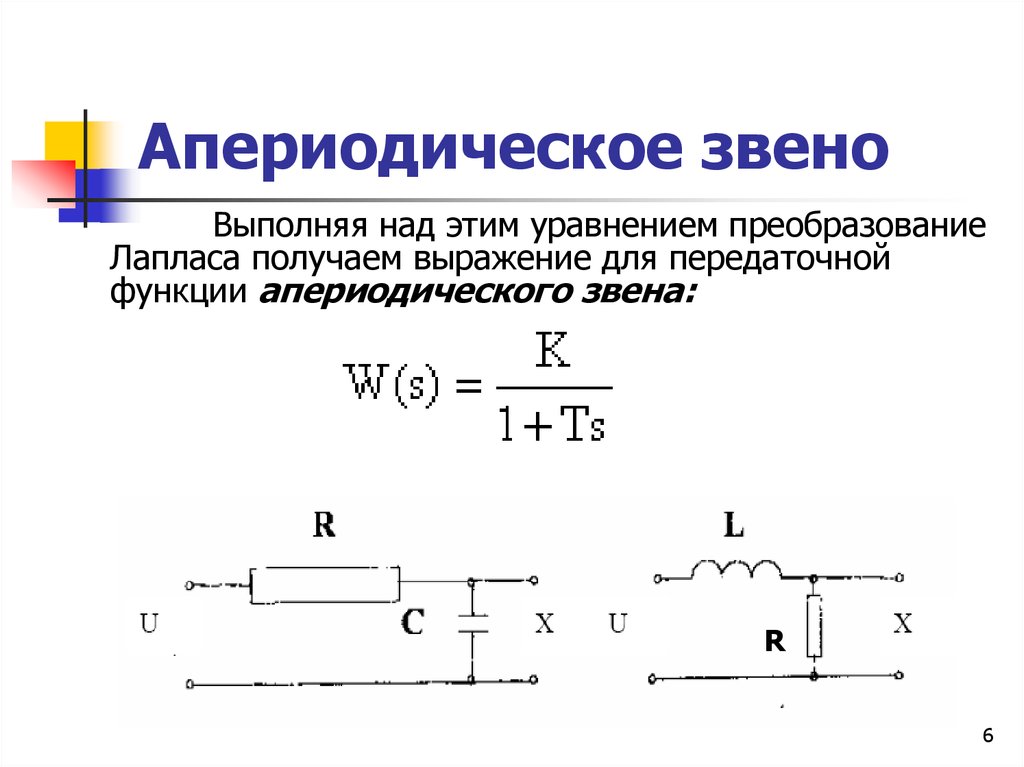
6. Апериодическое звено
Выполняя над этим уравнением преобразованиеЛапласа получаем выражение для передаточной
функции апериодического звена:
R
6
7. Апериодическое звено
Для нахождения временных характеристик звенаопределим его реакцию на единичное ступенчатое
воздействие. Изображение переходной функции
определяется как:
U
Корни характеристического уравнения
определяются как
7
8. Апериодическое звено
Выполняя обратное преобразование изображенияпереходной характеристики
получаем:
Выполняя аналогичные преобразования над изображением
импульсной переходной функции получаем выражение для
определения импульсной переходной функции
e –t/T
e –t/T
8
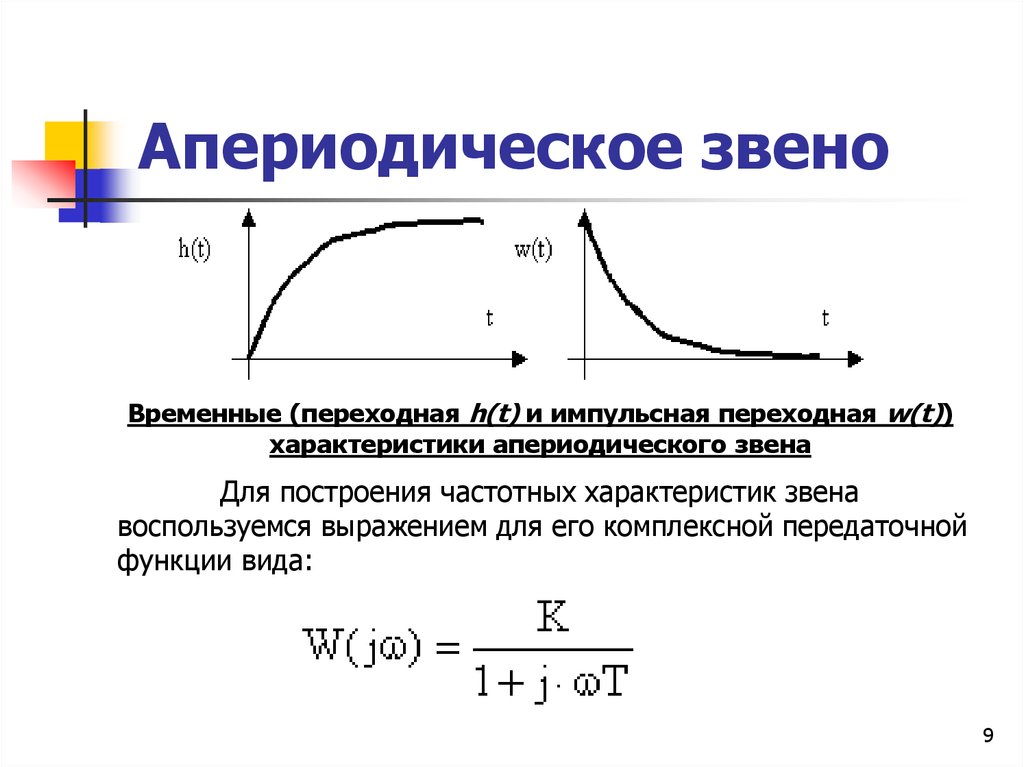
9. Апериодическое звено
Временные (переходная h(t) и импульсная переходная w(t))характеристики апериодического звена
Для построения частотных характеристик звена
воспользуемся выражением для его комплексной передаточной
функции вида:
9
10. Апериодическое звено
Амплитудно-частотная характеристика (АЧХ)апериодического звена определяется как:
Вещественная P(ω) и мнимая Q (ω) частотные
характеристики звена определяются как
10
11. Апериодическое звено
АФЧХ звена определяется какВыражение для расчета ЛАЧХ и ЛФЧХ принимает вид:
Для построения асимптотической ЛАЧХ воспользуемся
выражением вида:
11
12. Апериодическое звено
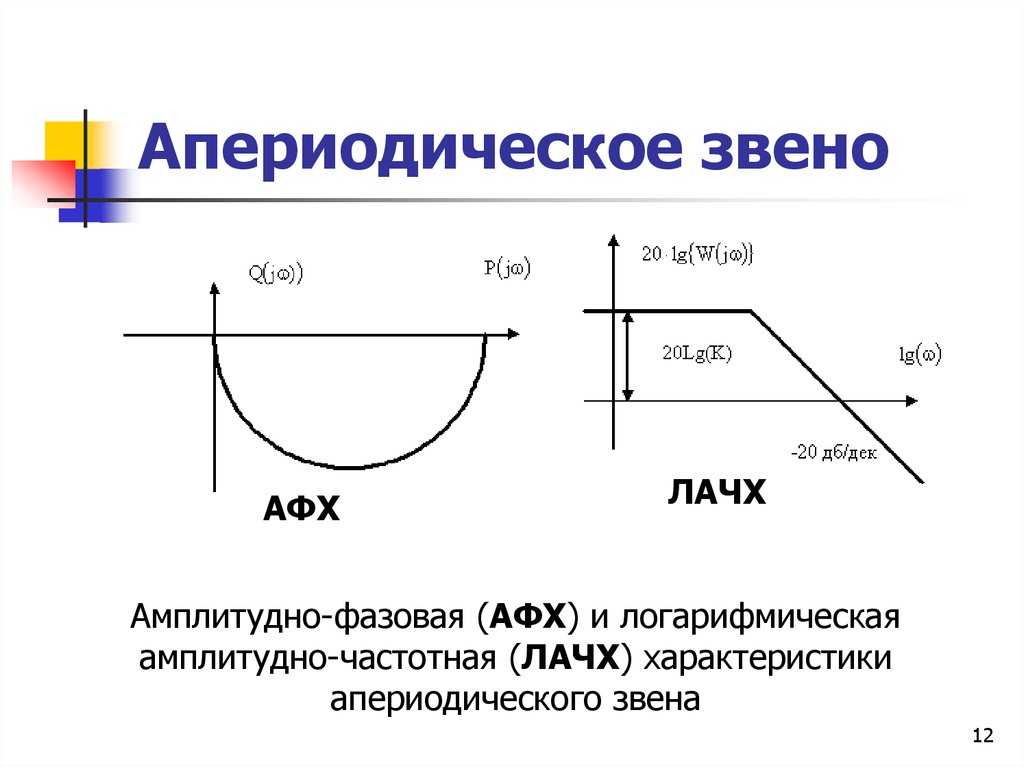
АФХЛАЧХ
Амплитудно-фазовая (АФХ) и логарифмическая
амплитудно-частотная (ЛАЧХ) характеристики
апериодического звена
12
13. Апериодическое звено
Большинство тепловых объектов являютсяапериодическими звеньями.
Например, при подаче на вход электрической печи
напряжения ее температура будет изменяться по
апериодическому закону.
Примерами апериодических звеньев также
являются исполнительные двигатели, усилители
мощности, магнитные усилители и т.п.
13
14. Интегрирующее звено
Уравнение движения для интегрирующего звена имеет видdX
kU
dt
Выполняя над этим уравнением преобразование Лапласа,
получаем выражение для передаточной функции звена следующего
вида:
Для нахождения временных характеристик звена определим
его реакцию на единичное ступенчатое воздействие. Переходная
характеристика звена определяется как
14
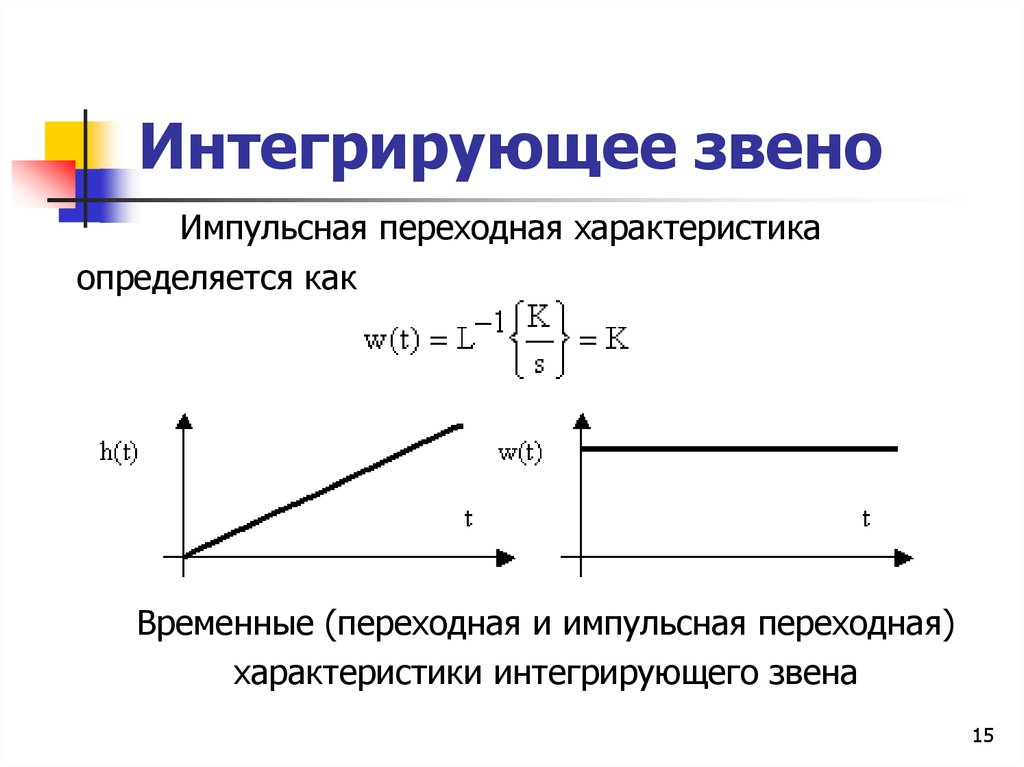
15. Интегрирующее звено
Импульсная переходная характеристикаопределяется как
Временные (переходная и импульсная переходная)
характеристики интегрирующего звена
15
16. Интегрирующее звено
Для построения частотных характеристик звена воспользуемсявыражением для его комплексной передаточной функции вида:
Исходя из этого, амплитудно-частотная характеристика звена
определяется как:
Вещественная P(ω) и мнимая Q (ω) частотные характеристики
звена определяются как
16
17. Интегрирующее звено
Выражение для расчета ЛАЧХ принимает вид:Для построения асимптотической ЛАЧХ
воспользуемся выражением вида:
АФХ
ЛАЧХ
17
18. Интегрирующее звено
При подаче на вход интегрирующего звенавоздействия - выходной сигнал с увеличением частоты
постоянно уменьшается по амплитуде. Это звено
астатическое, т.е. не имеет установившегося режима.
Примером интегрирующего звена является
двигатель постоянного
возбуждением.
тока
с
независимым
18
19. Колебательное звено
Уравнение движения для колебательного звенаимеет вид
2
d X
dX
T
2 T
X kU
2
dt
dt
2
T - постоянная времени звена
- коэффициент демпфирования
Выполняя над этим уравнением преобразование
Лапласа, получаем выражение для передаточной
функции звена следующего вида:
19
20. Колебательное звено
Колебательное звеноДля нахождения временных характеристик звена определим
его реакцию на единичное ступенчатое воздействие. Корни
характеристического уравнения звена определяются как:
1
2
20
21. Колебательное звено
Для колебательного звена характерно различноераспределение корней при разных комбинациях его параметров.
В общем случае переходная характеристика определяется
выражением вида:
1 2
— декремент затухания
— частота собственных колебаний
— начальная фаза колебаний
21
22. Колебательное звено
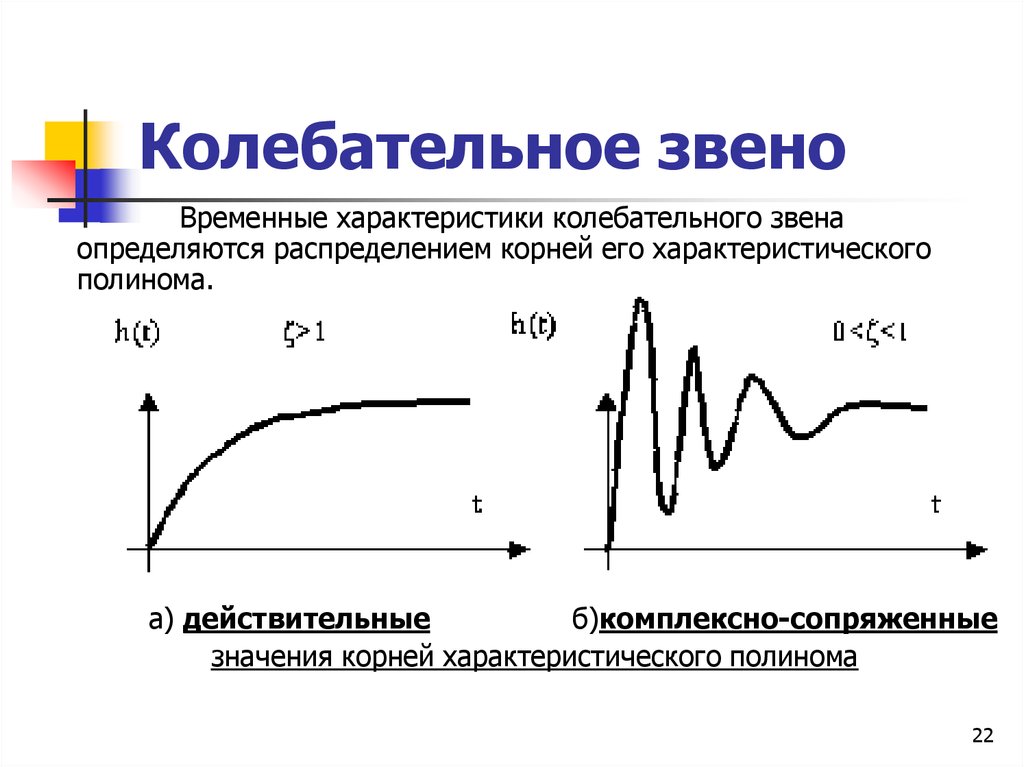
Временные характеристики колебательного звенаопределяются распределением корней его характеристического
полинома.
а) действительные
б)комплексно-сопряженные
значения корней характеристического полинома
22
23. Колебательное звено
Для построения частотных характеристик звена воспользуемсявыражением для его комплексной передаточной функции вида:
Исходя из этого, амплитудно-частотная характеристика
колебательного звена определяется как:
23
24. Колебательное звено
Вещественная P(ω) и мнимая Q (ω) частотныехарактеристики звена определяются как
Выражение для расчета ЛАЧХ принимает вид:
24
25. Колебательное звено
Для построения асимптотической ЛАЧХ воспользуемсявыражением вида:
»
АФХ
ЛАЧХ
25
26. Дифференцирующее звено
Уравнение движения для дифференцирующего звена имеет видX
dU
Выполняя над этим уравнением преобразование Лапласа
получаем выражение для передаточной функции звена следующего
вида:
Для нахождения временных характеристик звена определим его
реакцию на единичное ступенчатое воздействие. Переходная
характеристика дифференцирующего звена определяется как
26
27. Дифференцирующее звено
Переходная характеристики дифференцирующего звенаДля построения частотных характеристик звена воспользуемся
выражением для его комплексной передаточной функции вида:
27
28. Дифференцирующее звено
Исходя из этого, амплитудно-частотная характеристика звенаопределяется как:
Вещественная P(ω) и мнимая Q (ω) частотные характеристики
звена определяются как
Выражение для расчета ЛАЧХ принимает вид:
Для построения асимптотической ЛАЧХ воспользуемся выражением
вида:
28
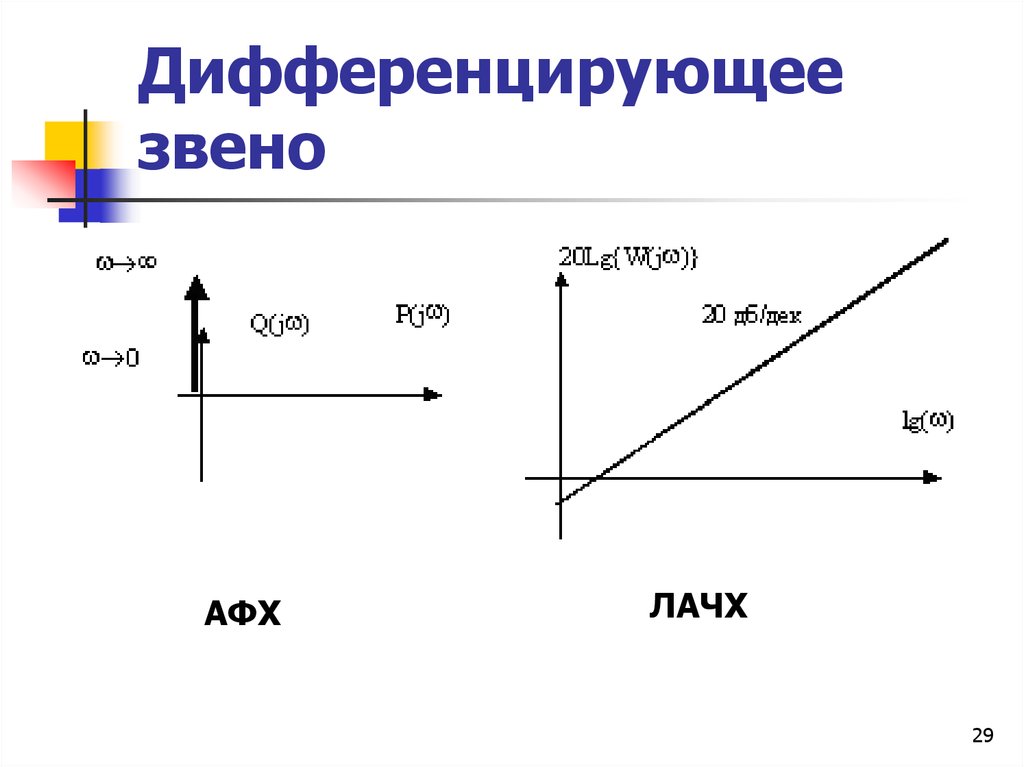
29. Дифференцирующее звено
АФХЛАЧХ
29
30. Дифференцирующее звено
Идеальные дифференцирующие звенья физически нереализуемы. Большинство объектов, которые
представляют собой дифференцирующие звенья,
относятся к реальным дифференцирующим звеньям.
.
Передаточная функция реального
дифференцирующего звена может иметь вид:
W(s)=
30
31. Усилительное (безинерционное) звено
Уравнение движения для усилительного звена имеет видX kU
Выполняя над этим уравнением преобразование Лапласа
получаем выражение для передаточной функции звена следующего
вида:
Для нахождения временных характеристик звена определим его
реакцию на единичное ступенчатое воздействие. Изображение
переходной функции определяется как
U
Выполняя обратное преобразование изображения переходной
характеристики, получаем:
31
32. Усилительное (безинерционное) звено
Выполняя аналогичные преобразования над изображениемимпульсной переходной функции, получаем выражение для
определения импульсной переходной функции w(t)
Для
построения
частотных
характеристик
звена
воспользуемся выражением для его комплексной передаточной
функции вида:
Исходя из этого, амплитудно-частотная характеристика
звена представляется точкой на комплексной плоскости.
32
33. Усилительное (безинерционное) звено
Логарифмическая частотная характеристикапредставляется прямой параллельной оси частот. Это
следует из выражения для определения
логарифмической частотной характеристики вида:
Выходной сигнал такого звена в точности
повторяет входной сигнал, усиленный в К раз.
Примерами таких звеньев являются:
механические передачи, датчики, безинерционные
усилители и др.
33
34. Запаздывающее звено
Уравнение движения звена имеет видX = U(t - 0)
Передаточная функция может быть
определена как
W(s) = e- 0s
Выходная величина X в точности
повторяет входную величину U с некоторым
запаздыванием
0.
Примером является конвейер.
34


























 Физика
Физика