Синтез систем автоматического управления

1. СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

1) Коррекция динамических свойств линейных
САУ
2) Корректирующие устройства
3) Синтез САУ на основе логарифмических
частотных характеристик

2. 1)Коррекция динамических свойств линейных САУ

Коррекция динамических свойств САУ осуществляется для
выполнения требований по точности, устойчивости и качеству
переходных процессов.
С точки зрения требований к точности САУ в установившихся
режимах коррекция динамических свойств САУ может понадобиться
для увеличения коэффициента передачи или порядка астатизма при
сохранении устойчивости и определенного качества переходных
процессов.
Коррекция применяется также как средство обеспечения
устойчивости неустойчивой системы или расширения области
устойчивости и повышения качества переходных процессов.
Любое устройство, включаемое в систему управления с целью
изменения ее свойств для обеспечения заданных показателей
качества, можно рассматривать как корректирующее.

3.

Наиболее часто в электромеханических системах управления
корректирующие устройства реализуются в виде пассивных или
активных четырехполюсников, содержащих резисторы, конденсаторы
(реже индуктивности) и в случае активных четырехполюсников –
операционные усилители.
По способу включения корректирующие устройства делятся на
- последовательные
– параллельные
–встречно-параллельные (местные обратные связи).

4.

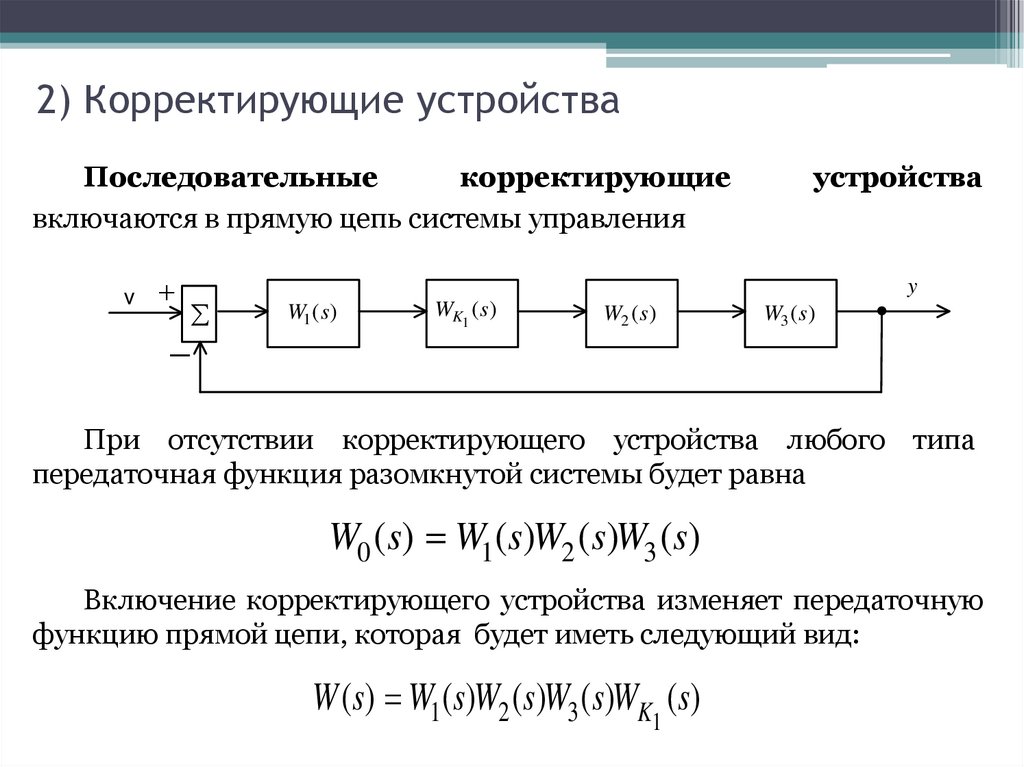
5. 2) Корректирующие устройства

Последовательные
корректирующие
включаются в прямую цепь системы управления
v
устройства
y
W1 ( s )
WK ( s )
1
W2 ( s )
W3 ( s )
При отсутствии корректирующего устройства любого типа
передаточная функция разомкнутой системы будет равна
W0 (s) W1 (s)W2 (s)W3 (s)
Включение корректирующего устройства изменяет передаточную
функцию прямой цепи, которая будет иметь следующий вид:
W (s) W1 (s)W2 (s)W3 (s)WK (s)
1

6.

Последовательная коррекция часто применяется для обеспечения
заданной точности системы.
В этом случае передаточная функция корректирующего устройства
выбирается в виде
передаточная функция разомкнутой скорректированной системы будет
Выбор величин K1 и ν обусловлен необходимой точностью системы в
установившихся режимах.
e oy 0
e y A
K0- коэффициент усиления
нескорректированной системы
V1 – амплитуда входного
воздействия

7.

Наряду с использованием последовательных корректирующих
устройств для повышения точности эти устройства могут
использоваться и для улучшения показателей качества системы.
В этом случае выбором передаточной функции корректирующего
устройства (КУ) изменяют среднечастотную часть исходной частотной
характеристики .
При этом применяют устройства с отставанием по фазе, с
опережением по фазе и с отставанием и опережением по фазе.
Передаточная функция такого устройства будет иметь вид

8.

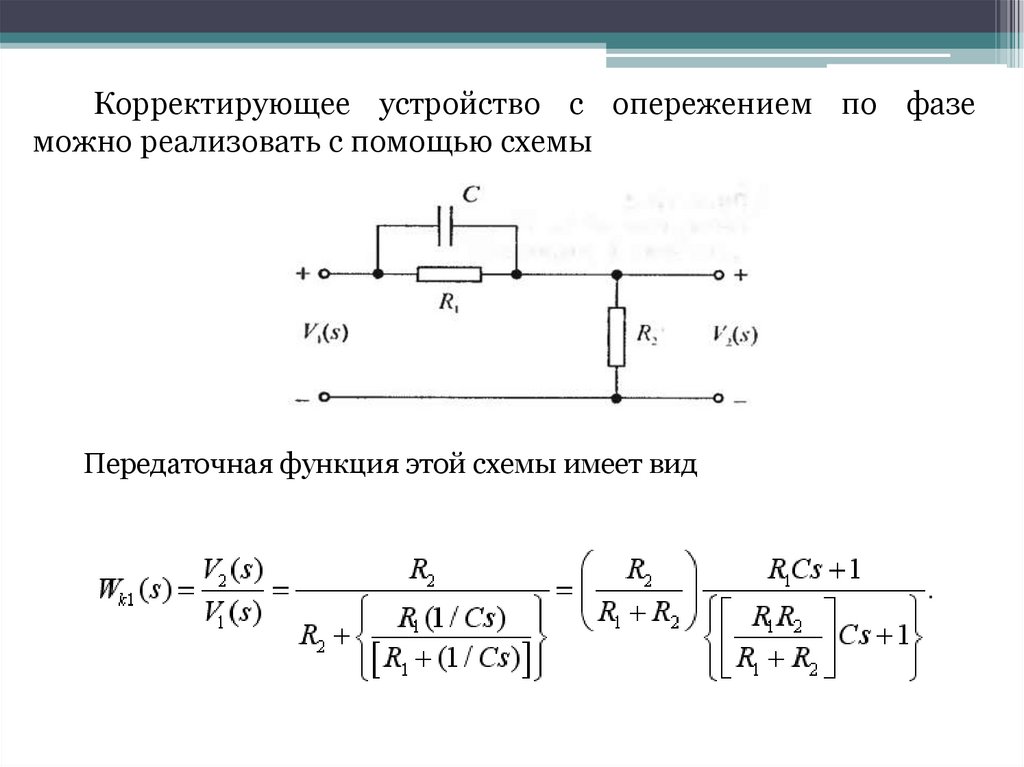
Частотная характеристика КУ с опережением по фазе

9.

Корректирующее устройство с опережением по фазе
можно реализовать с помощью схемы
Передаточная функция этой схемы имеет вид

10.

Полагая, что
R1
Получаем передаточную функцию КУ с опережением по фазе
Фазовый сдвиг имеет максимальное значение на частоте
Выражение для максимального фазового сдвига

11.

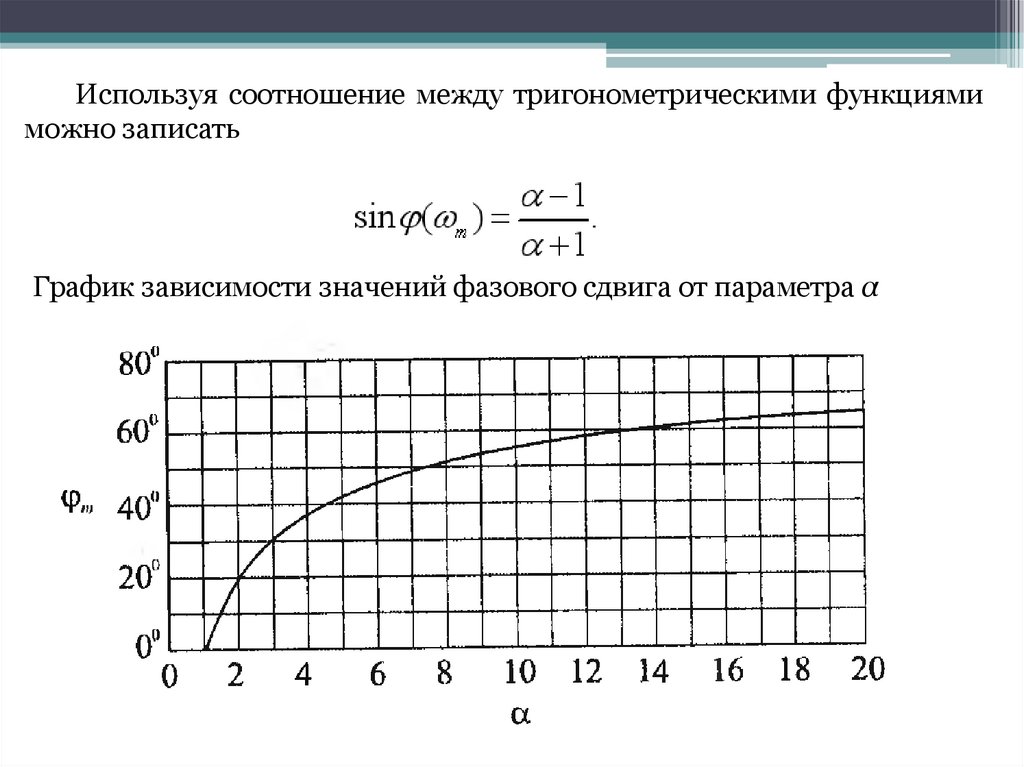
Используя соотношение между тригонометрическими функциями
можно записать
График зависимости значений фазового сдвига от параметра α

12.

13.

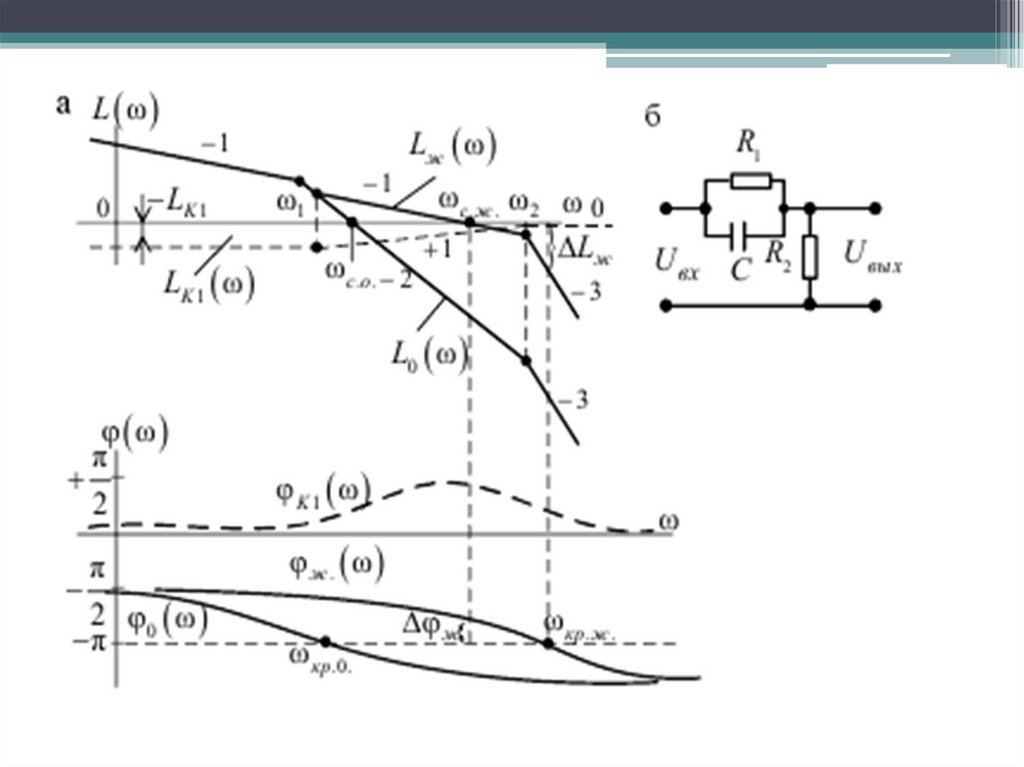
Корректирующее устройство с отставанием по фазе можно
реализовать с помощью схемы
Передаточная функция этой схемы имеет вид

14.

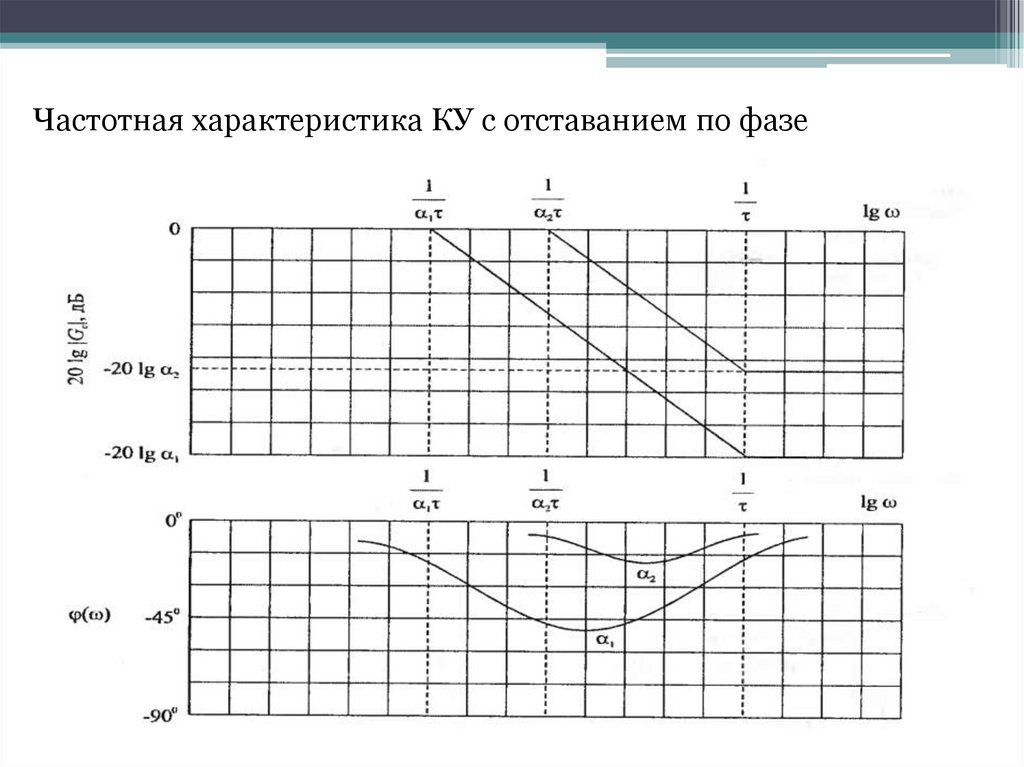
Частотная характеристика КУ с отставанием по фазе

15.

16.

17.

18.

19.

20.

21.

22.

Параллельные корректирующие устройства
Одним из распространенных способов улучшения качества системы
является введение производной от сигнала в прямой цепи.
Например
Тогда, передаточная функция разомкнутой системы
Введение корректирующего устройства изменяет амплитудную и фазовую
характеристики системы, которые примут вид

23.

Следует, что введение производной увеличивает положительные фазовые
сдвиги и позволяет при соответствующем выборе T’ в области частоты среза
системы «поднять» фазовую характеристику и увеличить запасы устойчивости.
При этом при малых частотах вид частотных характеристик исходной и
скорректированной системы не изменится.
Такая коррекция часто применяется для стабилизации или демпфирования
систем.
Другой вид параллельного корректирующего устройства, находящего
широкое применение, – это введение интеграла и производной от сигнала
прямой цепи.
Пусть
тогда передаточная функция прямой цепи будет равна

24.

Частотные характеристики будут иметь вид
В системе повышается порядок астатизма на единицу и соответственно
увеличивается точность.
При этом путем выбора величины T’ отрицательный фазовый сдвиг в
значительной степени можно на частоте среза скомпенсировать
положительным , что позволяет обеспечить устойчивость системы.
Встречно-параллельные корректирующие устройства.
Встречно-параллельные корректирующие устройства выполняются в виде
местных обратных связей.
Наиболее часто обратными связями охватывают силовую часть системы
управления (исполнительные элементы и усилители мощности).
Частотная характеристика участка, охватываемого обратной связью, имеет
вид

25.

Обычно в диапазоне рабочих частот системы (в диапазоне низких
частот) выполняется условие
и частотная характеристика
т.е.
характеристика участка цепи, охваченного обратной связью,
определяется только видом частотной характеристики корректирующего
элемента и не зависит от звена прямой цепи
В ряде случаев это позволяет скомпенсировать нежелательное влияние
звена на динамику системы, например, влияние малых нелинейностей или
малого изменения параметров этого звена прямой цепи.
В зависимости от вида передаточной функции
корректирующие
обратные связи делятся на жесткие и гибкие.

26.

Корректирующие устройства по внешнему воздействию
При изменении передаточной функции прямой цепи с помощью
последовательных,
параллельных
или
встречно-параллельных
корректирующих устройств для достижения заданных показателей качества
неизменным остается главный принцип построения системы – принцип
обратной связи (управление по отклонению).
Учет внешнего воздействия при коррекции, в частности применение
принципа компенсации (управление по возмущению) совместно с управлением
по отклонению, позволяет расширить возможности коррекции системы.
Системы, использующие как управление по отклонению, так и по
возмущению, относятся к классу комбинированных систем. Наиболее часто
комбинированное управление применяется для повышения точности системы
управления и уменьшения установившейся ошибки.
При определенных условиях с помощью комбинированного управления
можно свести установившуюся ошибку к нулю при любой форме внешнего
воздействия. Такое свойство называется инвариантностью системы по
отношению к внешнему воздействию.

27.

28.

Задача любой системы автоматического управления – как можно более
точно воспроизвести управляющий (полезный) сигнал и максимально ослабить
влияние возмущения на выходной сигнал. С этой точки зрения желательно,
чтобы в передаточная функция, связывающая Y(s) и V(s) была равна единице и
передаточная функция, связывающая Y(s) и F(s) была равна нулю.
Выполнением этих условий будут соответствовать соотношения:
Условия соответствуют так называемой полной инвариантности системы.

29.

В силу этого контур управления по отклонению, как правило,
используют для придания определенных динамических свойств системе, а
контуры коррекции по внешним воздействиям – для обеспечения точности.
Точное выполнение условий инвариантности практически невозможно
из условий физической реализуемости.
Поэтому условия инвариантности выполняются на практике с некоторой
погрешностью, в силу чего и инвариантность систем будет неполной, но
ошибки в системе с помощью корректирующих устройств по внешнему
воздействию могут быть значительно уменьшены.

30. 3) Синтез САУ на основе логарифмических частотных характеристик

Традиционные методы синтеза основаны на использовании
частотных логарифмических амплитудных характеристик (ЛАХ).
Общий порядок синтеза системы включает следующие этапы:
1) По виду передаточной функции исходной системы строится ЛАХ
исходной системы.
2) На основании требований к САУ строится желаемая ЛАХ
3) Путем сравнения характеристик
и
определяется
(если коррекция последовательная)
4) По виду
определяется структурная схема и параметры
коррекции.
5) Производится моделирование системы на ЦВМ уточняются
параметры САУ.
6) Производится реализация коррекции с помощью регуляторов или
программно.

31.

Рассмотрим подробнее построение желаемой ЛАХ.
а) Пусть даны рабочая частота p
и амплитуда
vp
задающего воздействия, а также допустимая ошибка
б) Пусть даны
в) Пусть для астатической САУ даны
vmax max
eдоп

32.

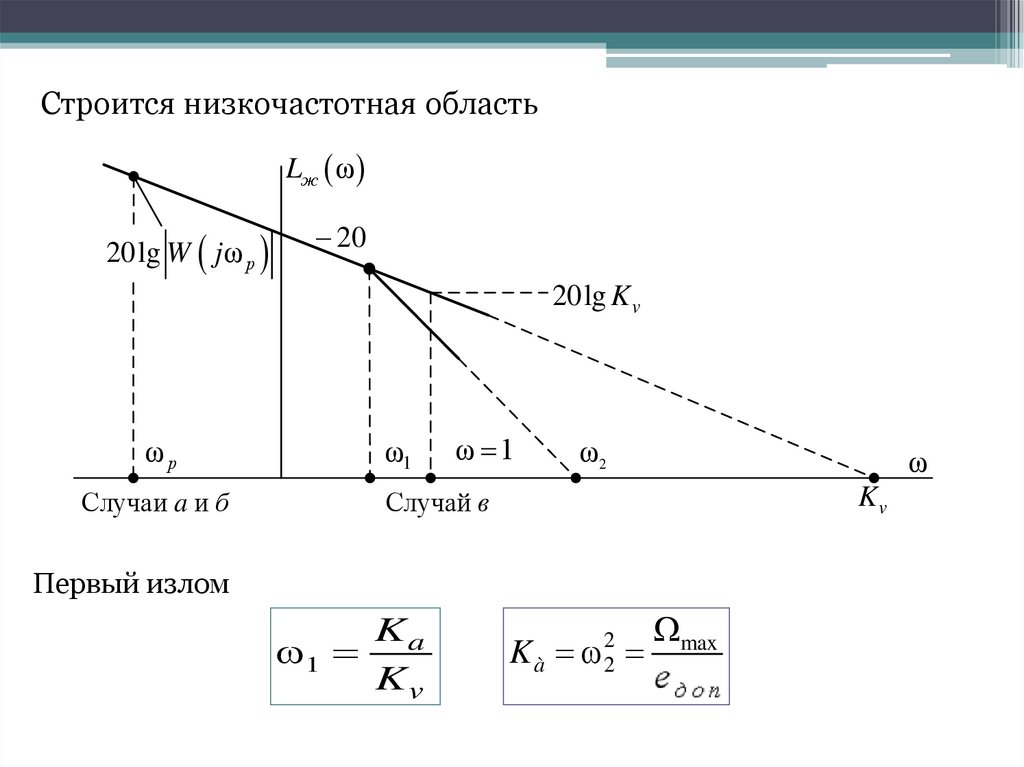
Строится низкочастотная область
Lж ω
20lg W jω р
20
20lg K v
ωр
Случаи a и б
ω1
ω 1
ω2
ω
Kv
Случай в
Первый излом
Ka
1
Kv
K à 22
max
eäî ï

33.

Первая частота при однократном изломе
Ka
1
Kv
K à 22
max
eäî ï
Первая частота при двукратном изломе
Kà
1 2
Kv
Учет требований качества переходного процесса (времени
переходного
процесса,
перерегулирование,
показатель
колебательности,
запасы
устойчивости)
учитываются
при
формировании среднечастотного участка желаемой ЛАЧХ.
Для этого пользуются номограммами.

34.

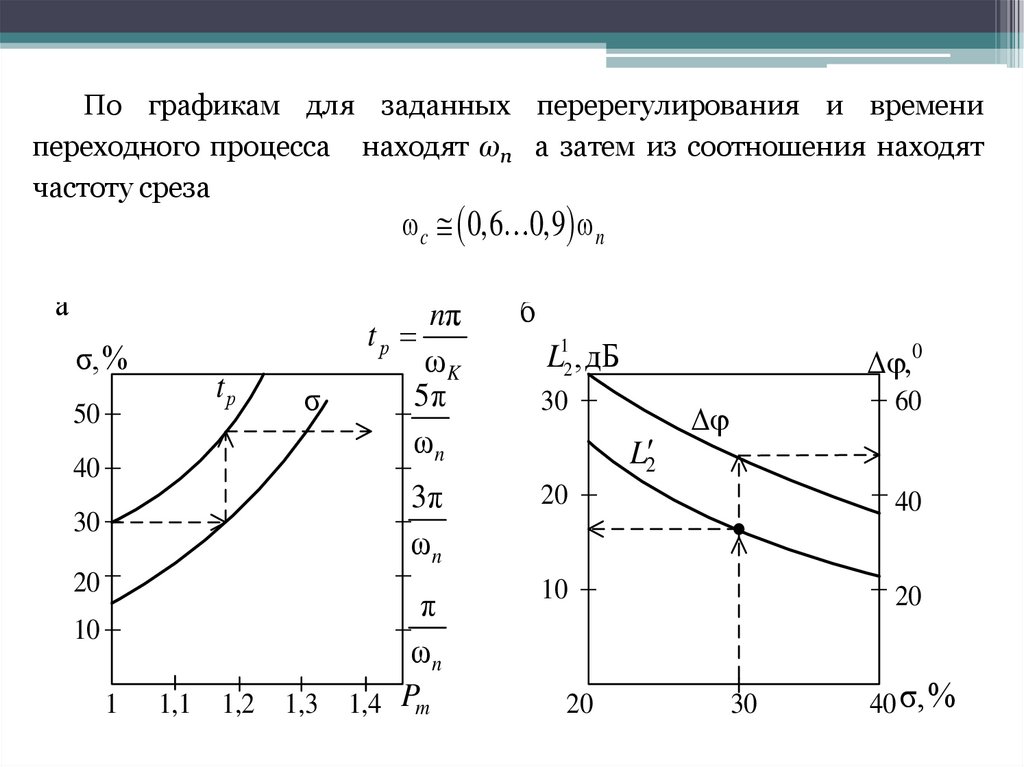
По графикам для заданных перерегулирования и времени
переходного процесса находят ωn а затем из соотношения находят
частоту среза
c 0,6 0,9 n
а
nπ
tр
σ,%
ωK
tр
5π
σ
50
ωn
40
3π
30
ωn
20
π
10
ωn
1 1,1 1,2 1,3 1,4 Pm
б
L12 ,дБ
30
20
L2
,0
60
40
10
20
20
30
40 σ,%

35.

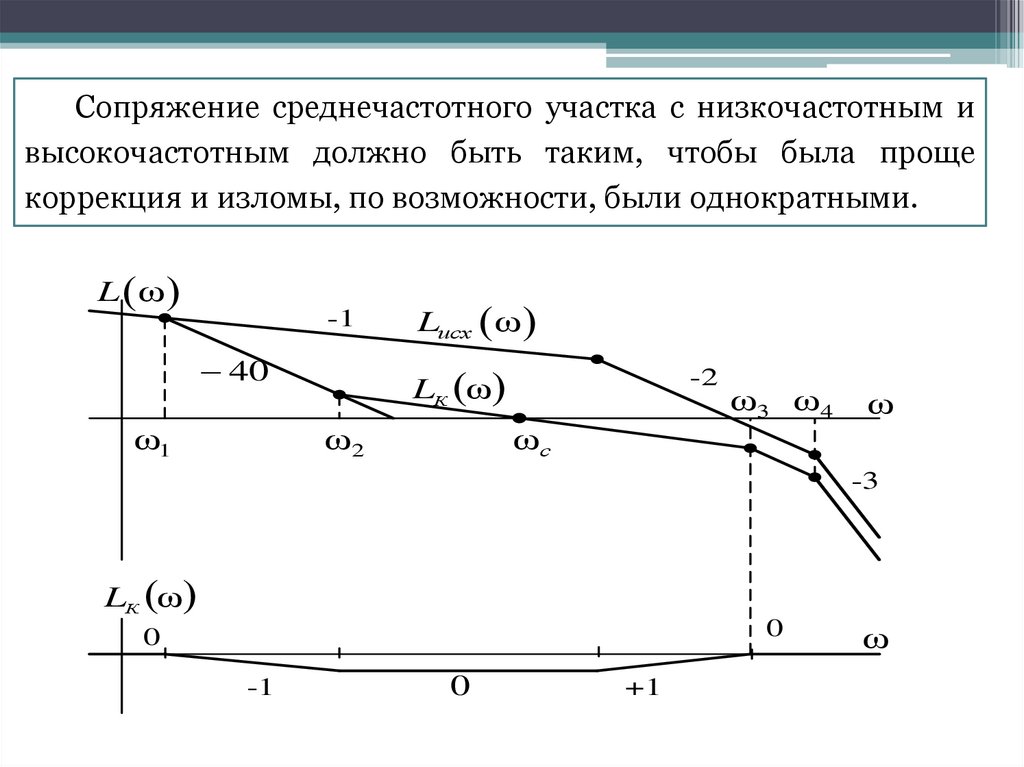
Сопряжение среднечастотного участка с низкочастотным и
высокочастотным должно быть таким, чтобы была проще
коррекция и изломы, по возможности, были однократными.
L ω
-1
40
ω1
Lисх ω
LК ω
ω2
-2
ω3 ω 4
ω
ωс
-3
LК ω
0
0
-1
0
+1
ω

36.

Для облегчения процедуры синтеза коррекции вводятся типовые передаточные функции исходной системы и соответствующие им передаточные
функции желаемой системы:

37.

Пример 1. Синтез
по заданным значениям ошибки
и частотного показателя качества M
Исходные данные:
Скорость изменения воздействия на входе системы с астатизмом
первого порядка не превышает значения
, а ускорение –
Требуется построить желаемую ЛАХ и определить передаточную
функцию желаемой системы, удовлетворяющей следующим
показателям качества:
максимальная ошибка
показатель колебательности
Передаточная функция исходной системы

38.

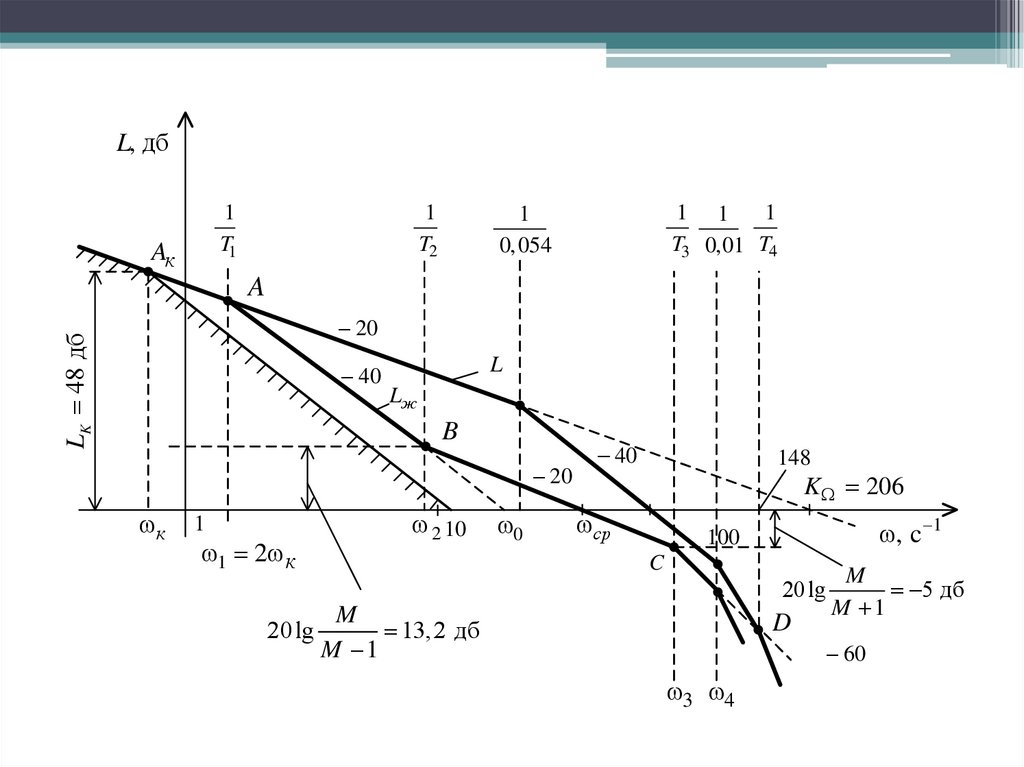
Решение.
Общий коэффициент разомкнутой системы
Координаты контрольной точки
частота
ордината
По этим данным строим запретную зону, в которую не должна попадать
желаемая ЛАХ. Для этого на частоте ωk =0.8 откладываем ординату Lk.
Проводим две прямые с наклоном -20 дб/дек и -40 дб/дек.

39.

L, дб
1
T1
Aк
1
T2
1 1
1
T3 0, 01 T4
1
0, 054
A
LK 48 дб
20
40
L
Lж
B
20
к
1
1 2 к
2 10
0
40
148
K 206
ср
, c 1
100
C
20 lg
20 lg
M
13, 2 дб
M 1
D
M
5 дб
M 1
60
3 4

40.

Первую сопрягающую частоту ω 1 принимаем равной 2*ωk
Допустимое значение первой постоянной времени
Через точку А проводим асимптоту с наклоном -40 дб/дек и находим
базовую частоту
В соответствии с требованием принимаем показатель колебательности
M = 1,28 и находим границы среднечастотной асимптоты:

41.

Определяем частоту сопряжения ω2 как абсциссу точки В, полученной при
пересечении асимптоты с наклоном -40 дб/дек верхней границы
среднечастотной асимптоты:
Требуемое значение второй постоянной времени
Строим среднечастотную асимптоту с единым наклоном до пересечения с
нижней границей в точке С, абсцисса которой определяет частоту сопряжения

42.

Третья постоянная времени
Строим ЛАХ исходной системы и формируем высокочастотные асимптоты
желаемой ЛАХ так, чтобы их наклоны совпадали с наклонами
высокочастотных асимптот исходной системы.
В этом случае сопрягающая частота
а четвертая постоянная времени
Желаемая передаточная функция разомкнутой системы

43.

Пример 2. Синтез Wж(s) по допустимому значению установившейся
ошибки и требуемым показателям качества в переходных режимах:
Построить желаемую ЛАХ Lж(w) для системы с астатизмом первого
порядка, удовлетворяющей следующим условиям: допустимое значение
установившейся ошибки
при постоянной скорости
и ускорении
максимальное перерегулирование σ≤30%,
время регулирования переходного процесса tp ≤0,4 c.
Передаточная функция исходной нескорректированной системы

44.

Решение.
Определяем добротности системы:
по скорости
по ускорению
Для дальнейших расчетов принимаем:
Определяем первую сопрягающую частоту желаемой ЛАХ

45.

Из таблицы находим допустимое значение частоты среза
39
42
46
50
55
5,1
4,2
3,6
3,0
2,2
37
32
26
20
18
Определяем вторую сопрягающую частоту

46.

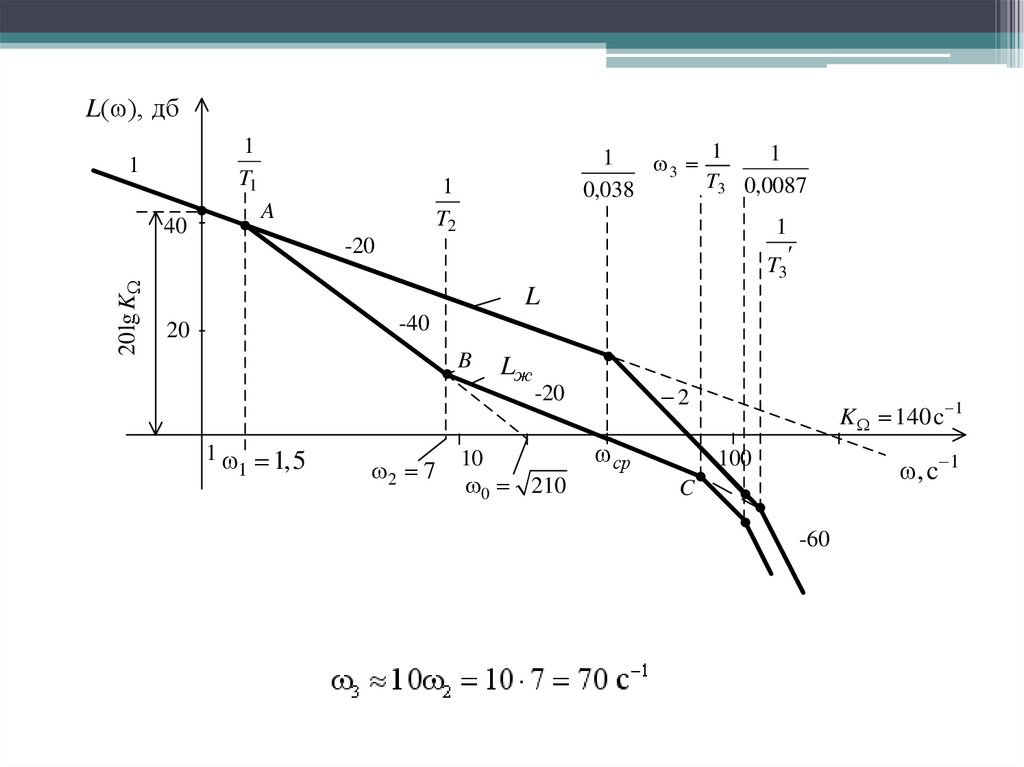
L( ), дб
1
T1
1
20 lg K
40
1
1
1
3
T3 0,0087
0,038
1
T2
A
1
-20
T3
L
-40
20
B
1 1,5
1
2 7
Lж
2
-20
10
0 210
ср
K 140 c 1
, c 1
100
C
-60

47.

Проверяем условие сохранения запасов устойчивости
Условие соблюдается.
По желаемой ЛАХ записываем передаточную функцию