Похожие презентации:
Синтез линейных стационарных автоматических систем
1.
Автоматика и управлениеТема 7. Синтез линейных
стационарных автоматических систем
Лекция 9. Методика расчета последовательных корректирующих
устройств. Методика расчета параллельных корректирующих
устройств
2.
7.5. Синтез последовательного КУ методом ЛЧХПостановка задачи синтеза АС
Исходные данные :
1. Требования к качеству АС - времени регулирования tp,
перерегулированию hm, запасам устойчивости 3 и L3, максимально
допустимым значениям ошибок в установившемся режиме ex , ex ,…
max
max
2. Эксплуатационные ограничения, накладываемые особенностями
объекта управления и условиями его функционирования
xmax , x max , , ymax , y ,max ,...
Скорректировать АС с передаточной функцией разомкнутого контура
WН(p) путем синтеза последовательного КУ таким образом, чтобы
удовлетворить требования, предъявляемые к АС. В результате синтеза
должны быть определены структура, параметры последовательного КУ и
схема технической реализации.
X(p)
Wк(p)
WН(p)
WН(p) - передаточная функция
Y(p) неизменной части
корректируемой АС;
Wк(p) - передаточная функция
последовательного КУ
3.
ПФ разомкнутой скорректированной системы (назовём её желаемой) Wж(p)Wж(p) = Wк(p)Wн(p)
Wж ( р )
Wк ( p )
Wн ( р )
Lк( ) = Lж( ) – Lн( )
к( ) = ж( ) - н( )
Для минимально-фазовых АС характерна однозначная связь между L( ) и
( ), поэтому для синтеза КУ можно использовать только одну из ЛЧХ АС,
а именно ЛАХ – L( ). Поскольку для построения ЛАХ требуется минимум
расчетов, то данный метод нашел широкое применение на практике.
Солодовнико́в Влади́мир Ви́кторович (1910,
Владивосток — 1991) — профессор, заслуженный
деятель науки и техники РФ, почетный член РАН,
выдающийся кибернетик современности, один из
основателей советской автоматики, один из
основателей ЦНИИКА, первый заместитель
директора института по научной части (1956 —
1965 годы).
4.
Этапы синтеза КУ методом ЛАХ:1. Построение ЛАХ нескорректированной системы LН( ).
2. Построение желаемой ЛАХ Lж( ) с учетом требований,
предъявляемых к АС.
3. Проверка устойчивости и качества синтезированной АС
известными методами. Если заданные требования не
выполняются, то изменяется желаемая ЛАХ Lж( ).
4. Определение ЛАХ последовательного КУ Lк( ) .
5. Определение передаточной функции КУ Wк(р) по виду ЛАХ КУ
Lк( ).
6. Проверка соответствия скорректированной АС с ПФ
разомкнутой системы W(р)= Wк(р) WН(р) точными методами на
соответствие предъявляемым требованиям.
7. Выбор схемы реализации КУ (по таблицам) и расчет её
элементов.
Сложность синтеза состоит в удачном выборе желаемой ЛАХ Lж( )
5.
Построение желаемой ЛАХНеобходимо учесть два противоречивых требования:
1. Скорректированная система должна удовлетворить всем
заданным требованиям ...
2. КУ, получаемое в результате синтеза, должно быть
максимально простым в реализации.
Желаемую ЛАХ Lж( ) условно подразделяют на три части:
низкочастотную, среднечастотную и высокочастотную.
Низкочастотная часть Lж( ) определяет статические свойства
системы, т.е. принципиальную точность АС в установившемся
режиме: коэффициент усиления K, астатизм , ошибку в
установившемся режиме e(t)
6.
Среднечастотная часть Lж( ) определяет устойчивость, запасустойчивости, время регулирования и перерегулирование АС.
Основные параметры среднечастотной асимптоты - это ее
наклон, частота среза с и ее расположение на оси абсцисс
относительно границ среднечастотной асимптоты.
Чем больше наклон среднечастотной асимптоты и меньше ее
размах по частотам, тем хуже динамические свойства системы.
Наиболее целесообразным является наклон -20 дб/дeк.
Частота среза с определяет быстродействие системы. Чем
больше с, тем меньше время регулирования.
Все выше перечисленные связи и зависимости далеко не так
прямолинейны и однозначны, что делает выбор Lж( ) самым
ответственным этапом синтеза.
7.
Высокочастотная часть Lж( ) незначительно влияет надинамические свойства системы, но чем больше наклон ее
асимптоты, тем меньше потребная мощность исполнительного
устройства и влияние высокочастотных помех.
Зачастую, высокочастотную часть желаемой ЛАХ строят так,
чтобы она совпадала или была параллельной ЛАХ
неизменяемой части АС LН( ).
L,дб
=-20
1 - низкочастотная часть,
2 - сопрягающая часть,
3 - среднечастотная часть,
4 - высокочастотная часть.
20lgK =-20(l+1)
1
=-20
1
1
1
2
2
3
,с-1
c
3
4
=-20( +1)
8.
L,дб=-20
20lgK =-20(l+1)
1
=-20
1
1
1
2
2
3
,с-1
c
3
4
=-20( +1)
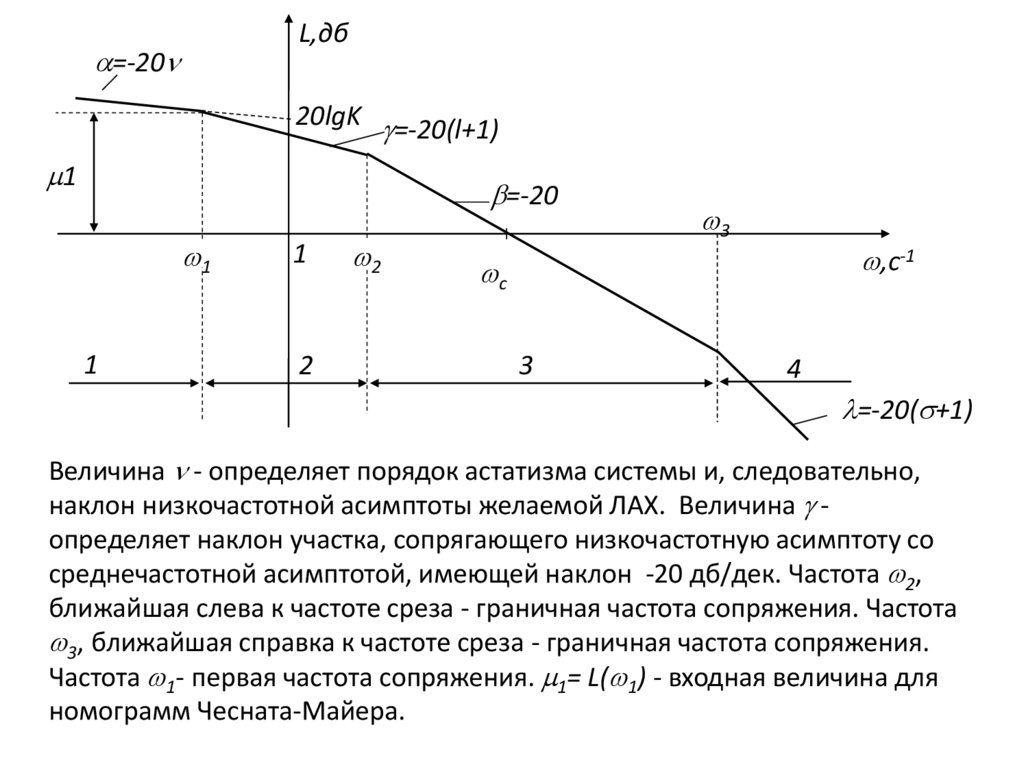
Величина - определяет порядок астатизма системы и, следовательно,
наклон низкочастотной асимптоты желаемой ЛАХ. Величина определяет наклон участка, сопрягающего низкочастотную асимптоту со
среднечастотной асимптотой, имеющей наклон -20 дб/дек. Частота 2,
ближайшая слева к частоте среза - граничная частота сопряжения. Частота
3, ближайшая справка к частоте среза - граничная частота сопряжения.
Частота 1- первая частота сопряжения. 1= L( 1) - входная величина для
номограмм Чесната-Майера.
9.
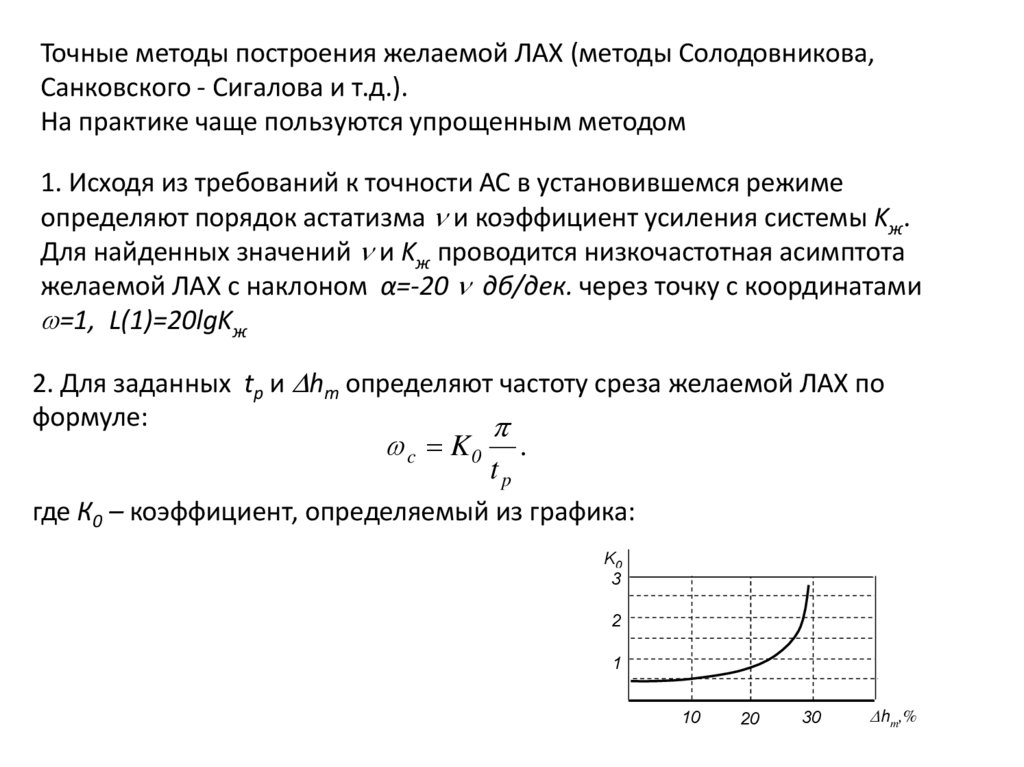
Точные методы построения желаемой ЛАХ (методы Солодовникова,Санковского - Сигалова и т.д.).
На практике чаще пользуются упрощенным методом
1. Исходя из требований к точности АС в установившемся режиме
определяют порядок астатизма и коэффициент усиления системы Kж.
Для найденных значений и Kж проводится низкочастотная асимптота
желаемой ЛАХ с наклоном α=-20 дб/дек. через точку с координатами
=1, L(1)=20lgKж
2. Для заданных tр и hm определяют частоту среза желаемой ЛАХ по
формуле:
c K0
tp
.
где К0 – коэффициент, определяемый из графика:
K0
3
2
1
10
20
30
hm,%
10.
3. Для обеспечения hm < 20 30 % наклон средней асимптоты должен быть=-20 дб/дек.
4. Определяют граничные частоты 3 и 2. Хорошие динамические свойства,
т.е. ( hm < 30%) и необходимый запас устойчивости ( 3 )
6
обеспечиваются в случае, если выполняются условия:
3=(2÷4) c,
2 0,1 3
длина среднечастотной асимптоты должна быть не менее одной декады.
5. Участки 1 и 3 сопрягают прямой с наклоном = -20 S дб/дек. Величину S
выбирают из условия обеспечения наибольшего запаса устойчивости по
фазе. Чем больше S, тем меньше запас устойчивости. Точка пересечения
участков 1 и 2 определяет частоту сопряжения 1
6. Наклон высокочастотной асимптоты желаемой ЛАХ, как правило,
совпадает с наклоном ЛАХ нескорректированной АС на этом участке.
Невыполнение данного условия существенно усложняет КУ
11.
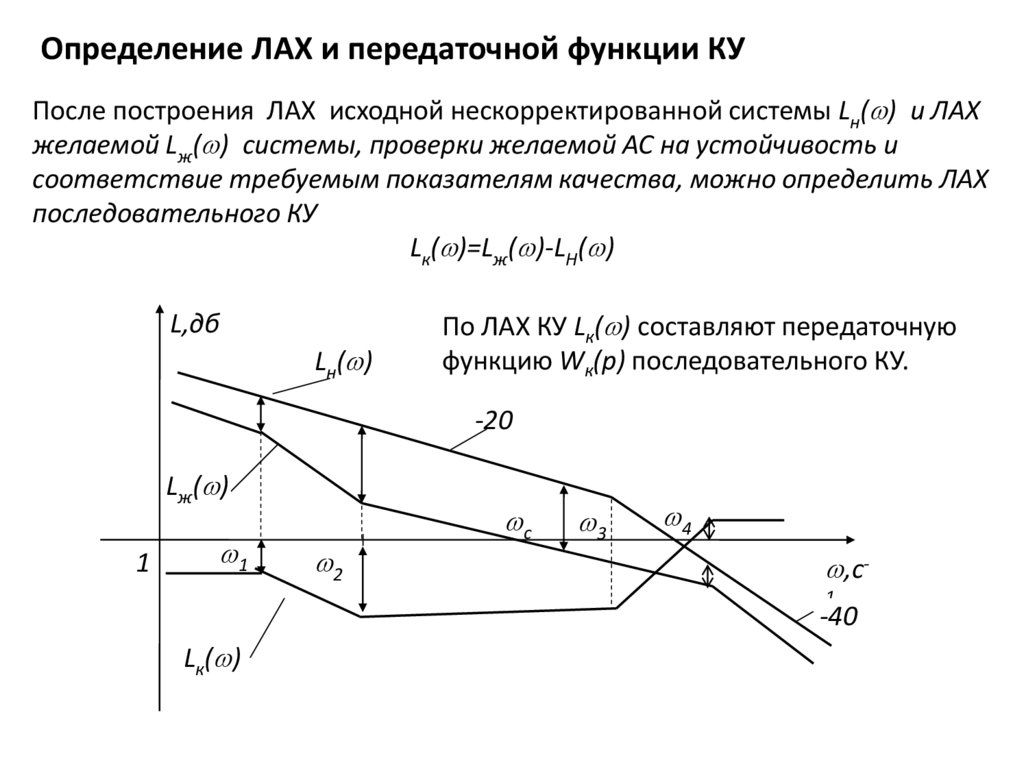
Определение ЛАХ и передаточной функции КУПосле построения ЛАХ исходной нескорректированной системы Lн( ) и ЛАХ
желаемой Lж( ) системы, проверки желаемой АС на устойчивость и
соответствие требуемым показателям качества, можно определить ЛАХ
последовательного КУ
Lк( )=Lж( )-LН( )
L,дб
Lн( )
По ЛАХ КУ Lк( ) составляют передаточную
функцию Wк(p) последовательного КУ.
-20
Lж( )
1
1
2
c
3
4
,с1
-40
Lк( )
12.
13.
Синтез АС по заданной точностиИсходными данными при синтезе АС по заданной точности являются:
1. Величины максимальных допустимых ошибок
ex
max
, e x
max
, …
2. Величины максимальных входных воздействий
хmax ,
(1)
(2)
хmax
, хmax
…
Ошибка АС в установившемся режиме
e(t) = S0 x(t) + S1 x(1)(t) +... = e xmax + e x max +….
ex
max
S 0 x max
e x
max
(1)
S 1 x max
…
Зная зависимость коэффициентов ошибки Si от параметров Kж и Ti
желаемой передаточной функции, из равенств можно определить значения
этих параметров.
14.
НапримерWж ( р )
где T1 >T2 > T3 >...>Tn
Кж(Т2 р 1)
n
р( Т 1 р 1 ) ( Ti p 1 )
i 3
Определить коэффициент усиления Kж разомкнутой АС при заданных
исходных данных
При рассмотрении временных процессов в установившемся режиме
малоинерционными звеньями с постоянными времени T3, T4, ..., Tn можно
пренебречь, тогда:
Кж(Т2 р 1)
Wж ( р )
р( Т 1 р 1 )
Определим передаточную функцию по ошибке желаемой АС:
1
р(Т1 р 1)
ФХЕ ( р)
1 Wж ( р)
р(Т1 р 1) К ж (Т 2 р 1)
Т1 р 2 р
2
S
S
p
S
p
.
0
1
2
Т1 р 2 (Т 2 К ж 1) р К ж
15.
- T1p2- p = (S0+S1p+S2p2+...)[T1p2+(T2Kж+1)p+Kж]0 S0 K ж , S0 0
p0
1
1 S 0 ( T2 K ж 1 ) S 1 K ж , S 1
,
Kж
p1
Используя
S0 xmax
ex
max
e x
max
(1)
S 1 x max
найдем коэффициент усиления
при необходимости Ti
(1)
хmax
Kж
е х max
Методика синтеза АС по заданной точности:
1. Исходя из заданного порядка астатизма АС определяется вид желаемой
передаточной функции по построенной Lж( )
2. Определяется передаточная функция по ошибке и коэффициенты ошибок Si .
3. Определяются значения неизвестных параметров.
16.
Синтез АС по заданному запасу устойчивостиЗадача: при заданных времени регулирования, а, следовательно, частоте
среза c, и порядке астатизма, синтезировать АС, у которой запас
устойчивости по фазе был бы не менее /6 (требования авиационных
систем)
Передаточная функция типовой желаемой АС
Wж ( р)
К ж (Т 2 р 1) S 1
n
р (Т1 р 1) S (Т 3 р 1) (Ti p 1)
T1 >T2 > T3 >...> Tn
i 4
- порядок астатизма АС по отношению к задающему воздействию,
S - величина, определяющая наклон участка сопрягающего
низкочастотную асимптоту со среднечастотной, имеющей наклон -20
дб/дек.
17.
Определим запас устойчивости по фазе типовой желаемой АС спередаточной функцией
Wж ( р)
К ж (Т 2 р 1) S 1
n
р (Т1 р 1) (Т 3 р 1) (Ti p 1)
S
i 4
3 ж ( с ) ( S 1)arctgT2 c S arctgT1 c
2
n
arctgT3 c arctgTi c ,
i 4
Ti
где
1
i
Параметры желаемой ЛАХ обычно выбирают так, чтобы выполнялись
неравенства:
c
c
1
1
i 3, n
1
i
тогда arctg
c
arctg = /2, arctg c
1
i
Пренебрегая величинами
n
c / i ,
i 4
c
i
3 ( S 1)arctg
i 3, n
c
S c .
2
2
2 3
18.
arctg c = arctg 22
c
2
Из тригонометрии
так как 2/ c<1
arctg
3 ( S 1 )arctg
2 2
c c
или arctg
c
2 2
2
c
c
S c .
2
2
2 3
2
c
3 ( S 1 ) 2 ( S )
2
3 ( S 1 )
c
2
2
c
3
c
3
Для обеспечения хороших динамических свойств АС частота 3 выбирается
из условия:
3 = (2 4) с
Принимая во внимание это условие и то, что запас ( S 1 ) 2 1 .
c 4 6
устойчивости АС должен превышать величину /6 2
19.
2 1.
( S 1 )
c 4 6
2
Значение частоты сопряжения 2 определяется при заданных и S.
Пример:
Положим =1 и S=1, тогда:
2
1
2 c
4 6
1
2 6 4 с > 2
0,8 с > 2 или 2< 0,2 3
На практике применяют более сильное неравенство
2< 0,1 3
Для обеспечения запаса устойчивости по фазе
3
6
необходимо чтобы протяженность среднечастотной асимптоты
желаемой ЛАХ была не менее одной декады при любых возможных v и S
20.
Последовательные КУ обладают рядом недостатков:1. Требуют дополнительных усилителей мощности по
причине ослабления мощности корректируемого сигнала.
2. Предъявляются жестокие требования к стабильности
параметров неизменяемой части АС.
3. Наличие форсирующих звеньев в КУ приводит к усилению
высокочастотных помех, которые перегружают оконечные
каскады.
Перечисленные недостатки последовательных КУ
ограничивают их практическое применение в системах средней
и большой мощности.
21.
7.6. Синтез параллельного КУ методом ЛЧХX(p)
W1(p)
Y(p)
W2(p)
WK(p)
Передаточная функция разомкнутой АС
W( p )
W1 ( p )W2 ( p )
1 W2 ( p )Wк ( p )
W1(p)W2(p)=Wн(p) - передаточная функция неизменяемой части системы;
Wк(p) - передаточная функция параллельного КУ
1
W
(
j
)
W
(
j
)
АФЧХ данной системы
н
1 W2 ( j )Wк ( j )
Если подобрать параллельное КУ так, чтобы
W ( j ) W1 ( j )
1
WК ( j )
W2 ( j )Wк ( j ) 1
динамические свойства звена, охваченного обратной
связью, определяются динамическими свойствами КУ
22.
Достоинства параллельных КУ1. Уменьшается зависимость качества корректируемой АС
от изменения ее параметров (в нашем случае от параметров
W2(p)).
2. Параллельные КУ не требуют дополнительных
усилителей мощности.
3. Значительно меньший, по сравнению с
последовательным КУ, уровень высокочастотных помех.
Различают жесткие и гибкие обратные связи
Жесткой обратной связью (ЖОС) называется параллельное КУ
с передаточной функцией вида:
Wк(p) = Kк
ЖОС действует как в установившемся, так и в переходном режимах.
Введение ЖОС приводит к уменьшению коэффициента усиления
разомкнутой системы и, следовательно, к незначительному 3 и
увеличению ошибки АС e(t) в установившемся режиме.
23.
Гибкой обратной связью (ГОС) называется параллельное КУс передаточной функцией вида:
Wк(p) = K1p+ K2p2+ K3 p3+...
Воздействие ГОС проявляется только в переходных режимах.
Поэтому, если необходимо изменить динамические свойства
АС без изменения точностных характеристик, применяют ГОС.
В силу того, что дифференцирующие звенья относятся к
технически нереализуемым звеньям, на практике вместо ГОС
используется изодромная обратная связь.
Изодромной обратной связью (ИОС) называется
параллельное КУ с передаточной функцией вида:
Кк р
Wк ( р )
Тр 1
24.
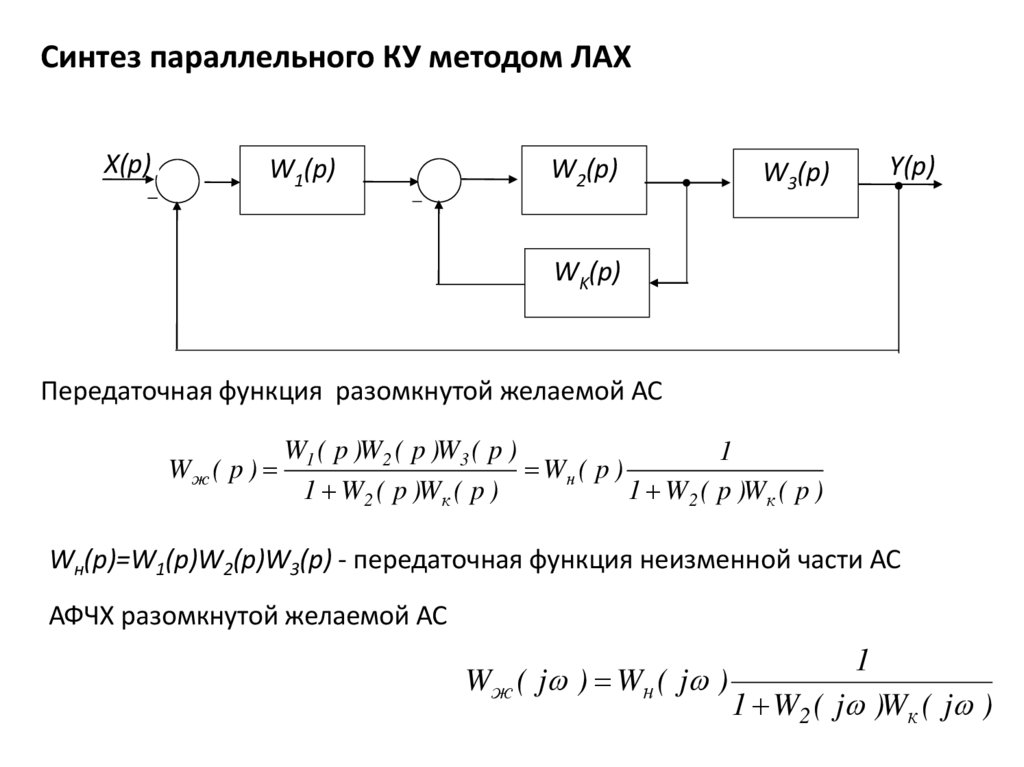
Синтез параллельного КУ методом ЛАХX(p)
W1(p)
W2(p)
Y(p)
W3(p)
WK(p)
Передаточная функция разомкнутой желаемой АС
Wж ( p )
W1 ( p )W2 ( p )W3 ( p )
1
Wн ( p )
1 W2 ( p )Wк ( p )
1 W2 ( p )Wк ( p )
Wн(p)=W1(p)W2(p)W3(p) - передаточная функция неизменной части АС
АФЧХ разомкнутой желаемой АС
Wж ( j ) Wн ( j )
1
1 W2 ( j )Wк ( j )
25.
Wж ( j ) Wн ( j )1
1 W2 ( j )Wк ( j )
Ось частот разбивается на два диапазона. На первом из них выполняется
условие:
W2 ( j )Wк ( j ) 1
тогда
Wж(j ) Wн(j )
L2( )+Lк( ) < 0 или Lк( ) < -L2( )
Lж( ) Lн( )
На втором диапазоне выполняется условие:
W2 ( j )Wк ( j ) 1
тогда
или
Wж ( j )
W1 ( j )W3 ( j )
Wк ( j )
Lж( ) = L1( )+L3( )-Lк( ) = L1,3( )-Lк( )
Lж( ) < Lн( )
для всего
диапазона частот
справедливо
неравенство:
Lж( ) Lн( )
L1,3 ( ) = L1( )+L3( )
26.
Неравенство Lж( ) Lн( ) говорит о том, что Wж(p) выбирают изэнергетических соображений таким образом, чтобы коэффициент усиления
Kж по возможности, не превышал коэффициент усиления разомкнутой
нескорректированной АС Kн . В этом случае для скорректированной АС не
потребуются дополнительные источники энергии.
Основные правила построения ЛАХ параллельного КУ Lк( ):
1. В диапазоне частот, где Lж( )=Lн( ) на ЛАХ КУ не накладывается никаких
ограничений, кроме простоты технической реализации и условия
Lк( )<-L2( )
2. В диапазоне частот, где Lж( )<Lн( ) ЛАХ КУ должна строиться так,
чтобы выполнялось условие
Lк( )=L1,3( )-Lж( )
и достижением максимального количества совпадений частот
сопряжений i для Lж( ) и L1,3( )
27.
Порядок синтеза АС с параллельным КУ :1. Построить ЛАХ неизменной части системы Lн( ), и Lж( ).
2. Проверить устойчивость и качество желаемой АС.
3. Построить ЛАХ звеньев, не охваченных КУ L1,3( ).
4. Построить ЛАХ звеньев, охваченных КУ L2( ) и определить L2( ).
5. Определить ЛАХ Lк( ) и передаточную функцию
параллельного КУ Wк(p), исходя из соображений:
- для областей частот где Lж( )=Lн( ), Lк( ) строится произвольно,
но с учетом условий Lк( ) < -L2( ) и простоты реализации КУ;
-для области частот где Lж( )<Lн( ), Lк( ) определяется
графическим решением уравнения
Lк( ) = L1,3( )-Lж( ).
По виду полученной Lк( ) находится Wк(p).
6. Проверить точными методами выполнение требований по
качеству синтезированной АС
7. С помощью таблиц определить и рассчитать схему
технической реализации параллельного КУ.
28.
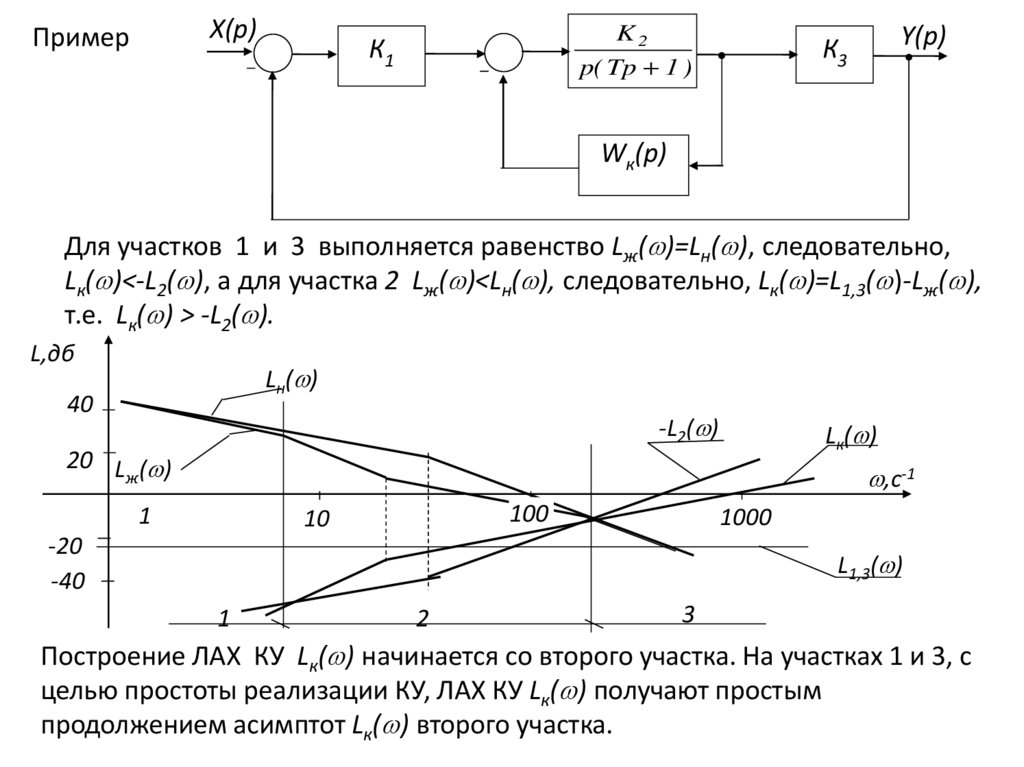
X(p)Пример
K2
p( Tp 1 )
К1
Y(p)
К3
Wк(p)
Для участков 1 и 3 выполняется равенство Lж( )=Lн( ), следовательно,
Lк( )<-L2( ), а для участка 2 Lж( )<Lн( ), следовательно, Lк( )=L1,3( )-Lж( ),
т.е. Lк( ) > -L2( ).
L,дб
Lн( )
40
-L2( )
Lк( )
20 L ( )
ж
,с-1
1
100
10
1000
-20
-40
L1,3( )
1
2
3
Построение ЛАХ КУ Lк( ) начинается со второго участка. На участках 1 и 3, с
целью простоты реализации КУ, ЛАХ КУ Lк( ) получают простым
продолжением асимптот Lк( ) второго участка.























 Электроника
Электроника








