Похожие презентации:
Система m линейных уравнений с n неизвестными
1. Система m линейных уравнений с n неизвестными
2.
Система m линейных уравнений с nпеременными имеет вид
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
21 1 22 2
2n n
2
,
.............................................
am1 x1 am 2 x2 amn xn bm
3.
Любые m переменных системы mлинейных уравнений с n переменными
(m<n) называются основными (или
базисными), если определитель
матрицы коэффициентов при них
отличен от нуля.
Тогда остальные n - m переменных
называются неосновными ( или
свободными)
4.
Базисным решением системы m линейныхуравнений с n переменными называется
решение, в котором все n-m неосновных
переменных равны нулю.
В задачах линейного программирования
особый интерес представляют допустимые
базисные решения (опорные планы).
Число базисных решений является
конечным.
Базисное решение, в котором хотя бы одна
из основных переменных равна нулю,
называется вырожденным.
5.
Геометрический методрешения задач
линейного
программирования
6.
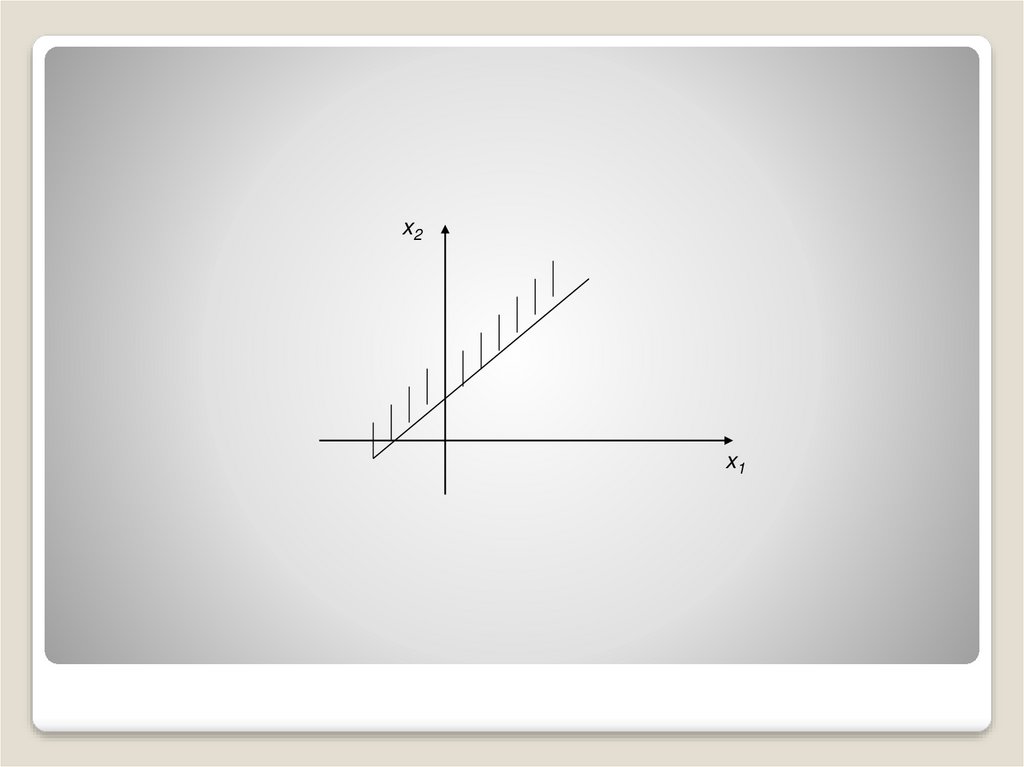
Решение неравенств7.
Множеством решений неравенстваa1x1 a2 x2 b1
с двумя переменными является одна из
полуплоскостей, на которые вся
плоскость делится прямой ,
a1x1 a2 x2 b1
включая и эту прямую
8.
x2x1
9.
Множеством решений совместнойсистемы m линейных неравенств с
двумя переменными
a11 x1 a12 x 2 b1
a x a x b
21 1
22 2
2
..........
..........
......
a m1 x1 a m 2 x 2 bm
10.
является выпуклый многоугольник (иливыпуклая многоугольная область)
11.
Множество всех допустимых решенийсовместной системы m линейных
уравнений с n переменными (m<n)
является выпуклым многогранником в
n- мерном пространстве.
12.
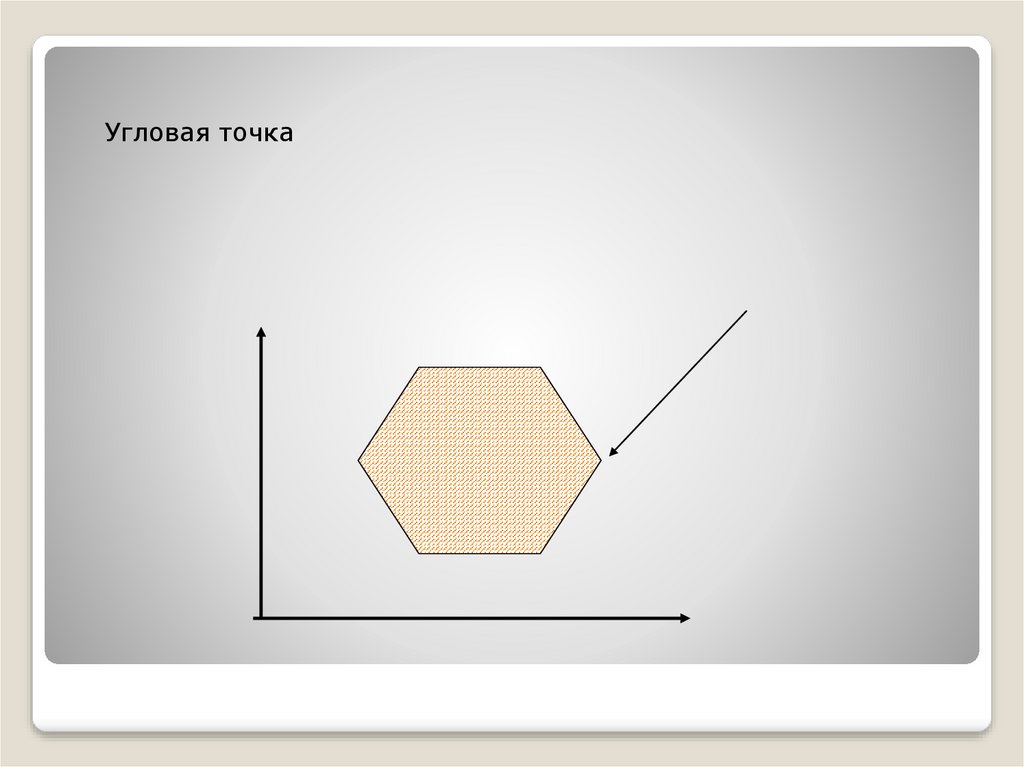
Угловая точка13.
Сформулированные теоремы и понятияпозволяют сделать следующие выводы.
14.
Если основная задача линейногопрограммирования имеет оптимальный
план, то максимальное или
минимальное значение целевая
функция задачи принимает в одной из
вершин многогранника решений (в
одной из угловых точек).
15.
Если максимальное значение целеваяфункция задачи принимает более чем в
одной вершине, то она принимает его
во всякой точке, являющейся выпуклой
линейной комбинацией этих вершин.
16.
Для определения этой вершинынеобходимо построить линию уровня
c1x1+ c2x2=h (где h – некоторая
постоянная), проходящую через
многоугольник решений,
17.
и будем передвигать ее в направлениивектора
d= (c1;c2),
до тех пор, пока она не пройдет через ее
последнюю общую точку с
многоугольником решений.
18.
Координаты указанной точки иопределяют оптимальный план данной
задачи.
19.
Заканчивая рассмотрениегеометрической интерпретации задачи ,
отметим, что при нахождении ее
решения могут встретиться случаи,
изображенные на рис. 1 - 4.
20.
Рис. 1 характеризует такой случай, когдацелевая функция принимает
максимальное значение в единственной
точке А.
21.
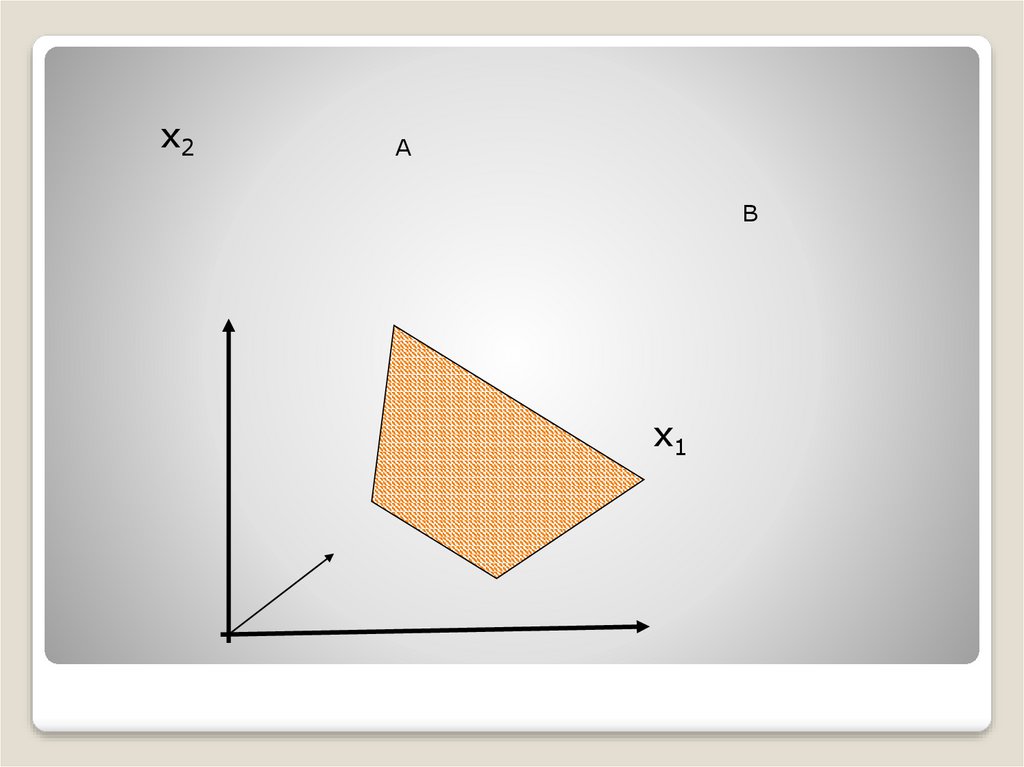
х2А
х1
22.
Из рис. 2 видно, что максимальноезначение целевая функция принимает в
любой точке отрезка АВ.
На рис. 3 изображен случай, когда
целевая функция не ограничена сверху
на множестве допустимых решений, а
на рис. 4 – случай, когда система
ограничений задачи несовместна.
23.
х2А
В
х1
24.
х2х1
25.
х2х1
26.
Таким образом, отмеченные вышеслучаи, встречающиеся при нахождении
максимального значения целевой
функции, имеют место и при
определении ее минимального
значения.
27.
Итак, нахождение решения задачилинейного программирования на
основе ее геометрической
интерпретации включает следующие
этапы:
28.
1. Строят прямые, уравнения которыхполучаются в результате замены в
ограничениях знаков неравенств на
знаки точных равенств.
29.
2. Находят полуплоскости, определяемыекаждым из ограничений задачи.
3. Находят многоугольник решений.
30.
4. Строят вектор целевой функцииd(c1;c2),.
5. Строят прямую c1x1+ c2x2=h,
проходящую через многоугольник
решений.
31.
6. Передвигают прямую в направлениивектора , в результате чего - или
находят точку (точки), в которой
целевая функция принимает
максимальное (минимальное) значение,
или устанавливают неограниченность
сверху (снизу) функции на множестве
планов.
32.
7. Определяют координаты точкимаксимума (минимума) функции и
вычисляют значение целевой функции в
этой точке.
33.
Для изготовления двух видов продукцииР1 и Р2 используют 4 вида ресурсов S1 ,
S2 , S3 и S4 .
Запасы ресурсов, число единиц ресурсов,
затрачиваемых на изготовление
единицы продукции, приведены в
таблице (цифры условные).
34.
Видресурса
Запас
ресурса
Число ед. ресурсов, затрачиваемых на
изготовление единицы продукции
P1
P2
S1
18
1
3
S2
16
2
1
S3
5
S4
21
1
3
35.
Прибыль, полученная от единицыпродукции Р1 и Р2 , - соответственно 2 и
3 руб.
Необходимо составить план
производства, при котором прибыль от
реализации будет максимальной.
36.
x1 3 x2 182 x x
16
1
2
x2 5
3 x1 21
x 0
1
x2 0
37.
F 2x1 3x2 max38.
Найдем решение сформулированнойзадачи, используя ее геометрическую
интерпретацию.
Сначала построим многоугольник
решений (область допустимых решений)
39.
Для этого в неравенствах системыограничений и условиях
неотрицательности переменных знаки
неравенств заменим на знаки точных
равенств и найдем соответствующие
прямые:
40.
x1 3 x2 182 x x 16
1
2
x2 5
3 x1 21
x 0
1
x2 0
41.
Х1+3х2=18Х1
0
3
х2
6
5
42.
х2х1+3х2=18
х1
43.
Чтобы определить искомуюполуплоскость, нужно взять какуюнибудь точку, принадлежащую одной из
полуплоскостей, и проверить,
удовлетворяют ли ее координаты
данному неравенству.
Если координаты взятой точки
удовлетворяют данному неравенству, то
искомой является та полуплоскость,
которой принадлежит эта точка, в
противном случае – другая
полуплоскость.
44.
х2х1+3х2=18
х1
45.
В результате получим:46.
х2х1+3х2=18
х1=7
х2=5
2х1+ х2=16
х1
47.
х2х1+3х2=18
х1=7
х2=5
2х1+ х2=16
х1
48.
х1+3х2=182х1+х2=16
х1=18-3х2
2(18-3х2)+х2=16
-5х2=-20
х2=4
х1= 6
F=2*6+3*4=24
49.
Область допустимых решений задачилинейного программирования имеет
вид:
Тогда максимальное значение
функции
равно…
50.
Область допустимых решений задачилинейного программирования имеет вид
Тогда максимальное значение функции
равно…
51.
Максимальное значение целевойфункции
при ограничениях
равно…
52.
Максимальное значение целевойфункции
при ограничениях
равно…
53.
Максимальное значение целевойфункции
при ограничениях
равно…
































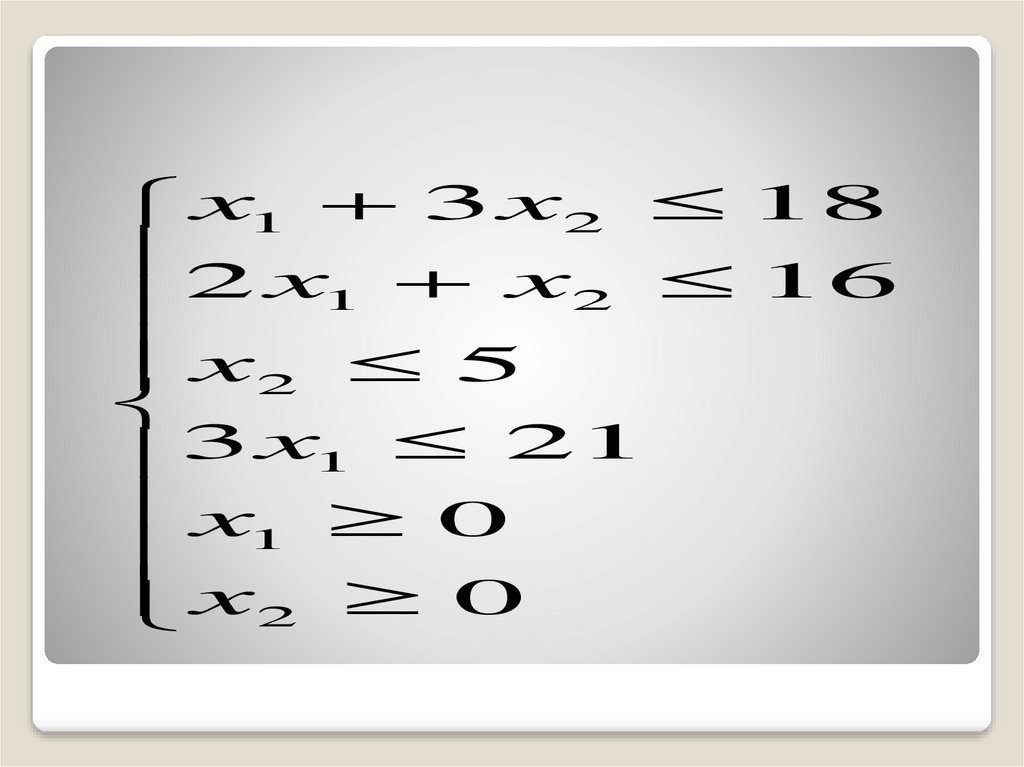
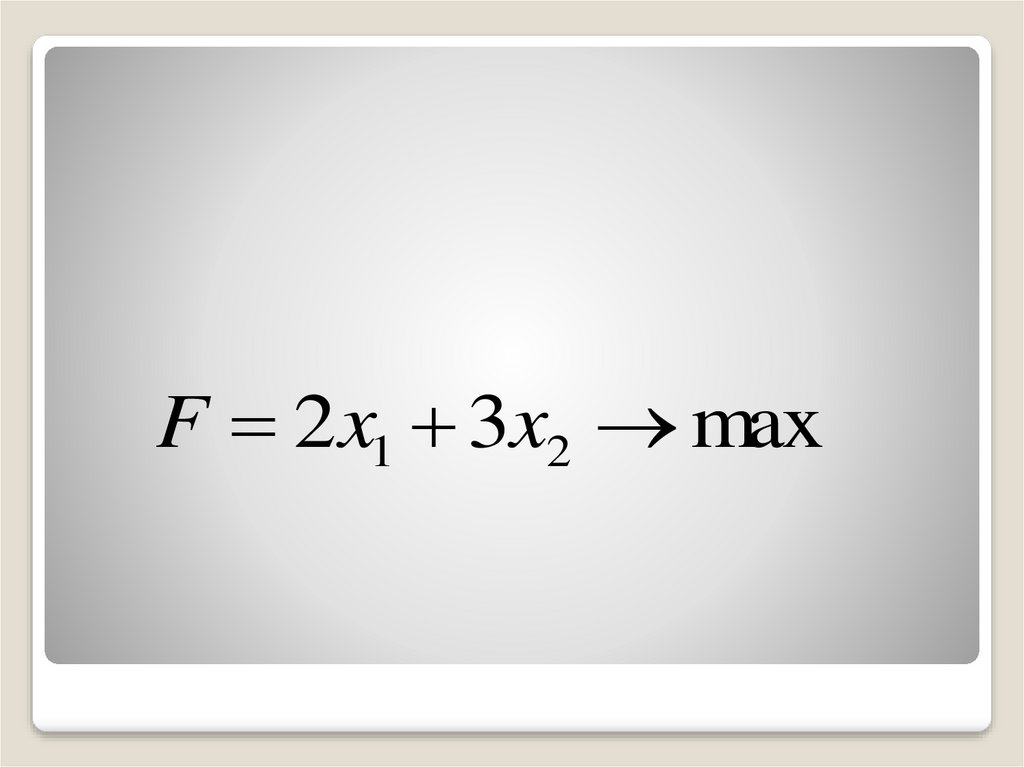


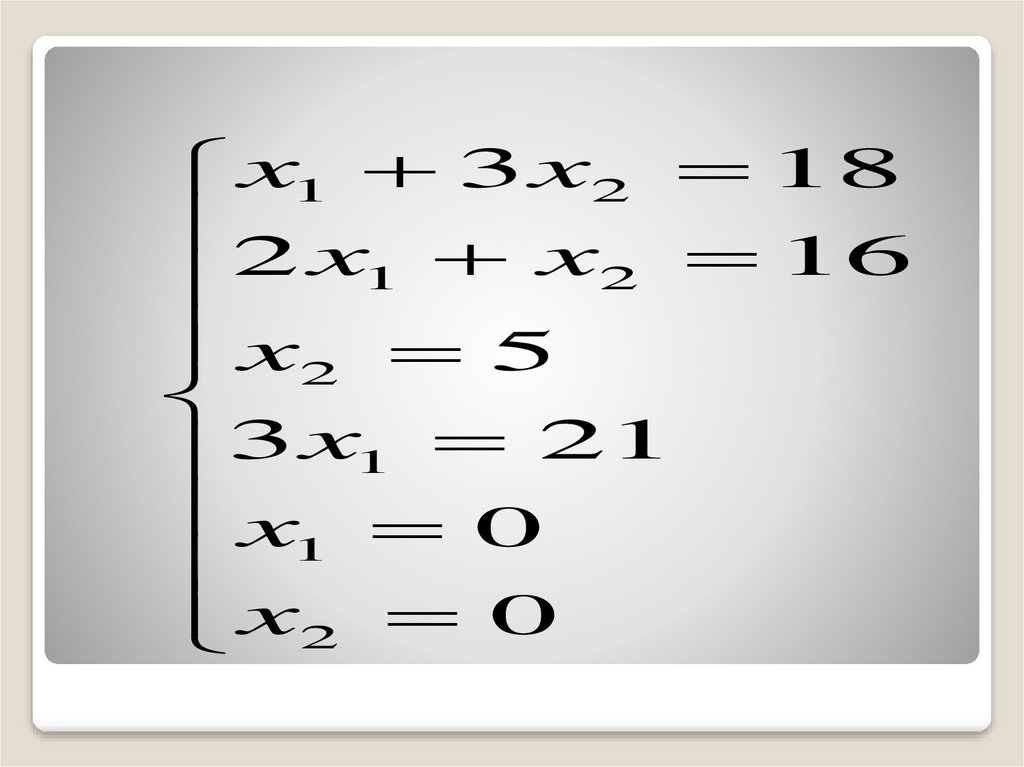







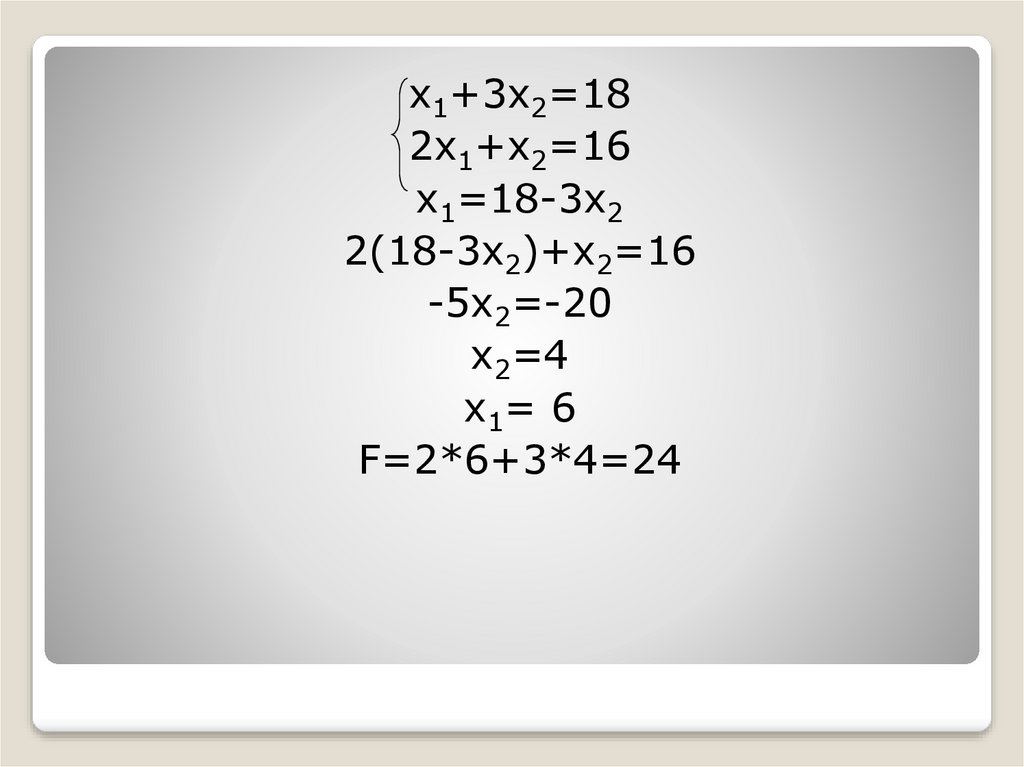





 Математика
Математика








