Плоскости и их проекции

1.

Плоскости и их проекции
Определителем плоскости называется совокупность геометрических
элементов, однозначно задающих положение плоскости в пространстве.
Плоскость считается заданной, если относительно произвольной точки
пространства можно однозначно решить вопрос о её принадлежности к этой
плоскости.
Плоскость называется плоскостью общего положения, если она
параллельна и не перпендикулярна ни к одной из плоскостей проекций.
Существуют следующие способы задания плоскости:
1) тремя точками, не лежащими на одной прямой, например, точками А, В и
С;
не

2.

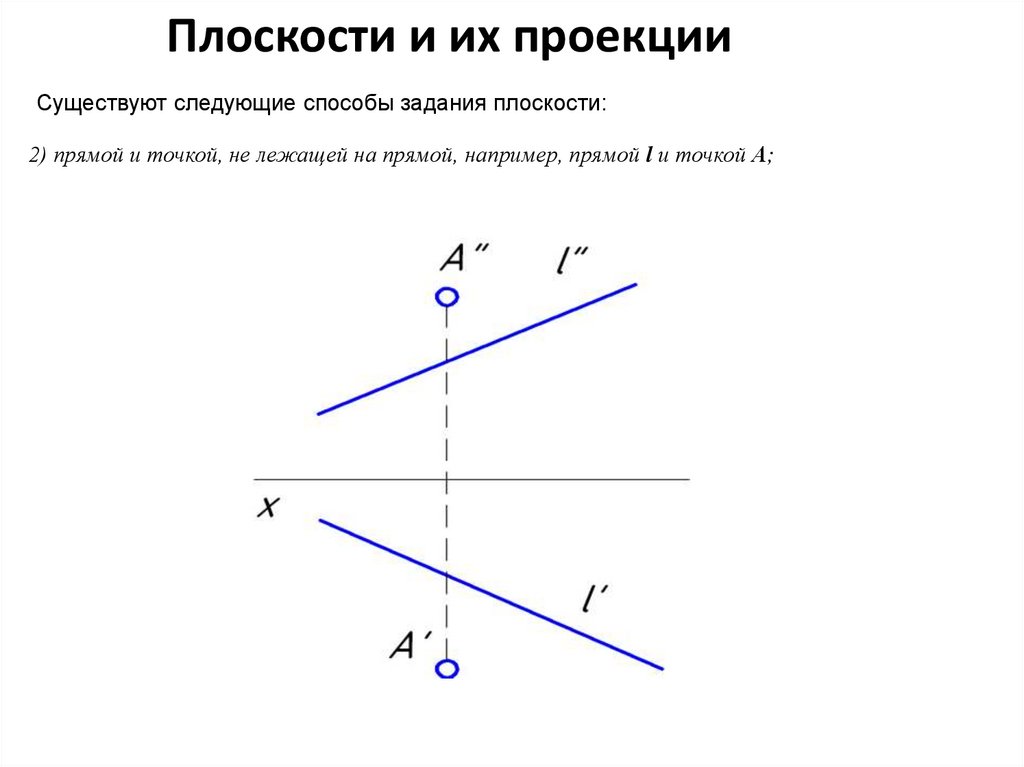
Плоскости и их проекции
Существуют следующие способы задания плоскости:
2) прямой и точкой, не лежащей на прямой, например, прямой l и точкой А;

3.

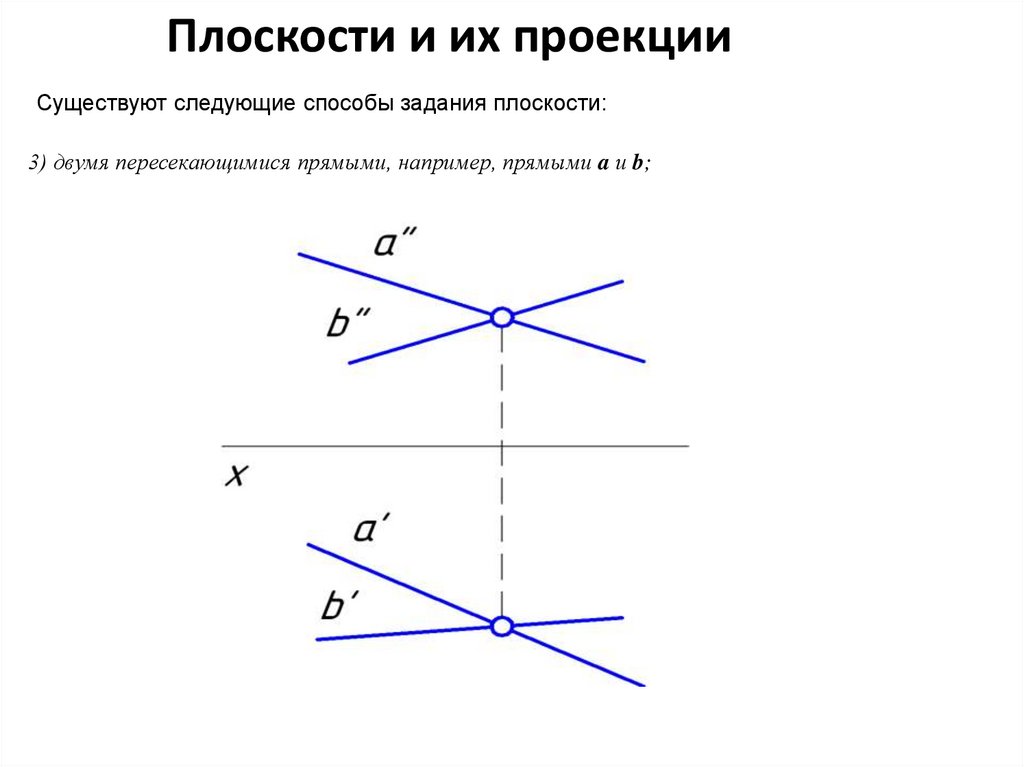
Плоскости и их проекции
Существуют следующие способы задания плоскости:
3) двумя пересекающимися прямыми, например, прямыми a и b;

4.

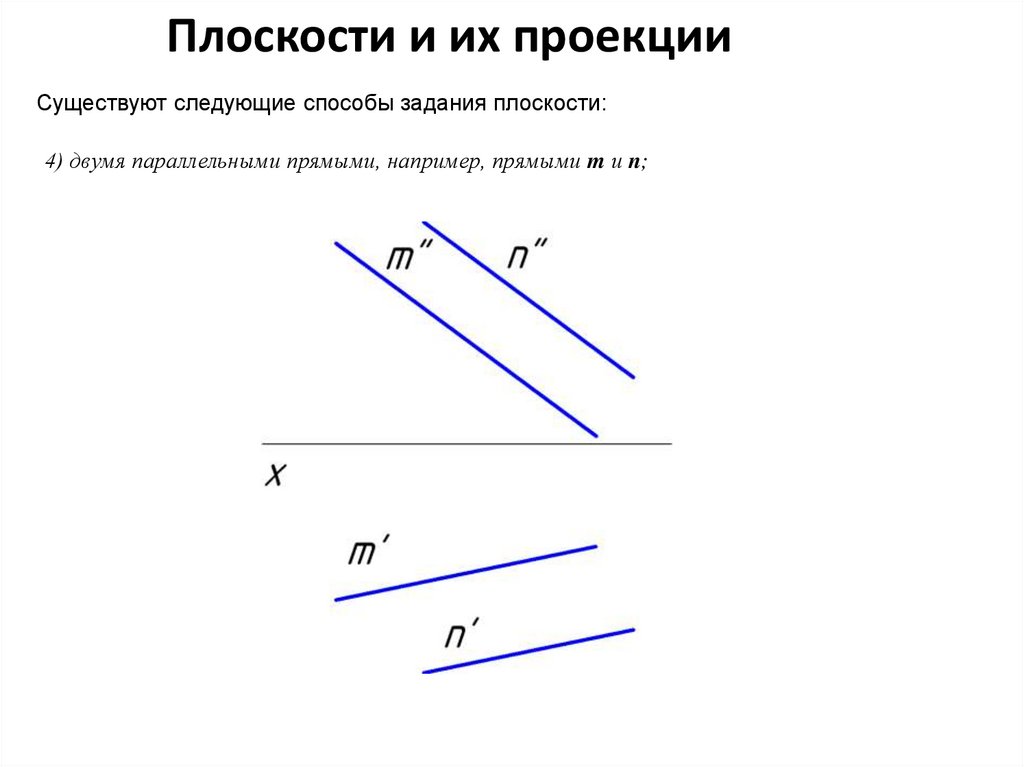
Плоскости и их проекции
Существуют следующие способы задания плоскости:
4) двумя параллельными прямыми, например, прямыми m и n;

5.

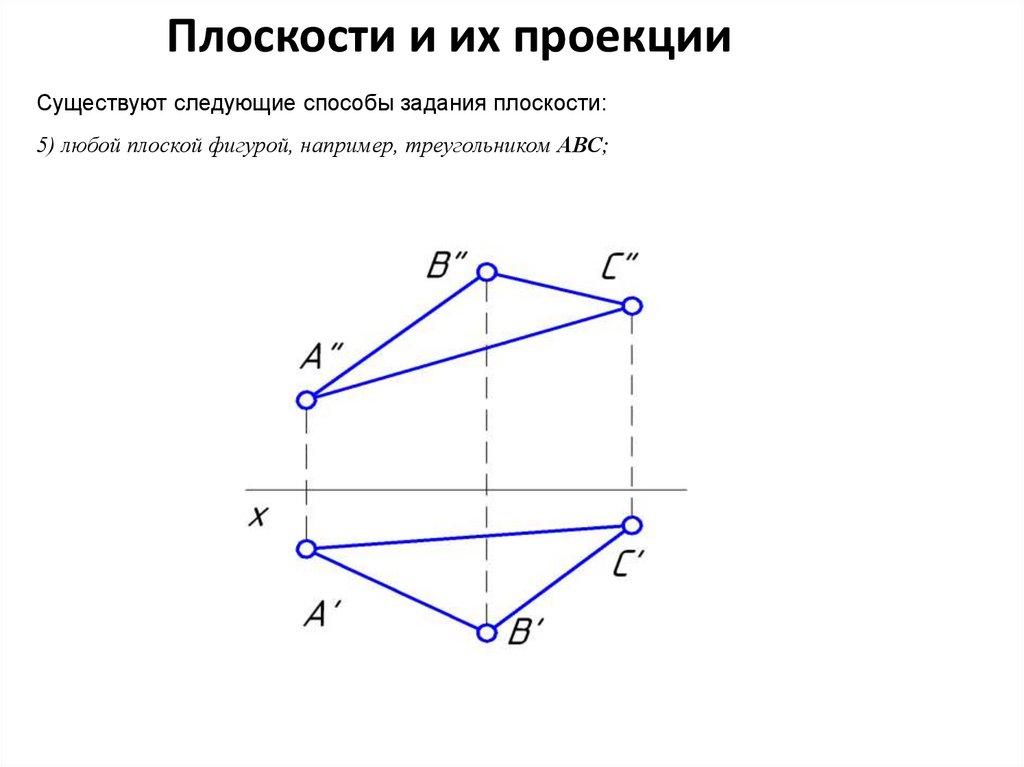
Плоскости и их проекции
Существуют следующие способы задания плоскости:
5) любой плоской фигурой, например, треугольником АВС;

6.

Плоскости и их проекции
Существуют следующие способы задания плоскости:
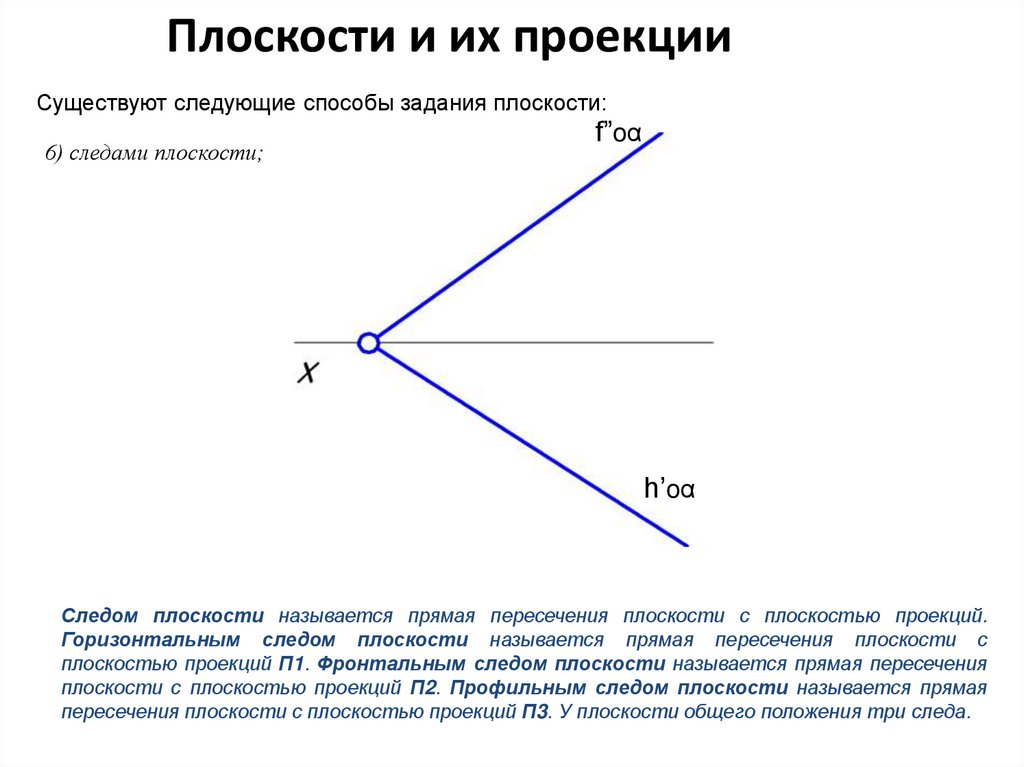
6) следами плоскости;
f”oα
h’oα
Следом плоскости называется прямая пересечения плоскости с плоскостью проекций.
Горизонтальным следом плоскости называется прямая пересечения плоскости с
плоскостью проекций П1. Фронтальным следом плоскости называется прямая пересечения
плоскости с плоскостью проекций П2. Профильным следом плоскости называется прямая
пересечения плоскости с плоскостью проекций П3. У плоскости общего положения три следа.

7.

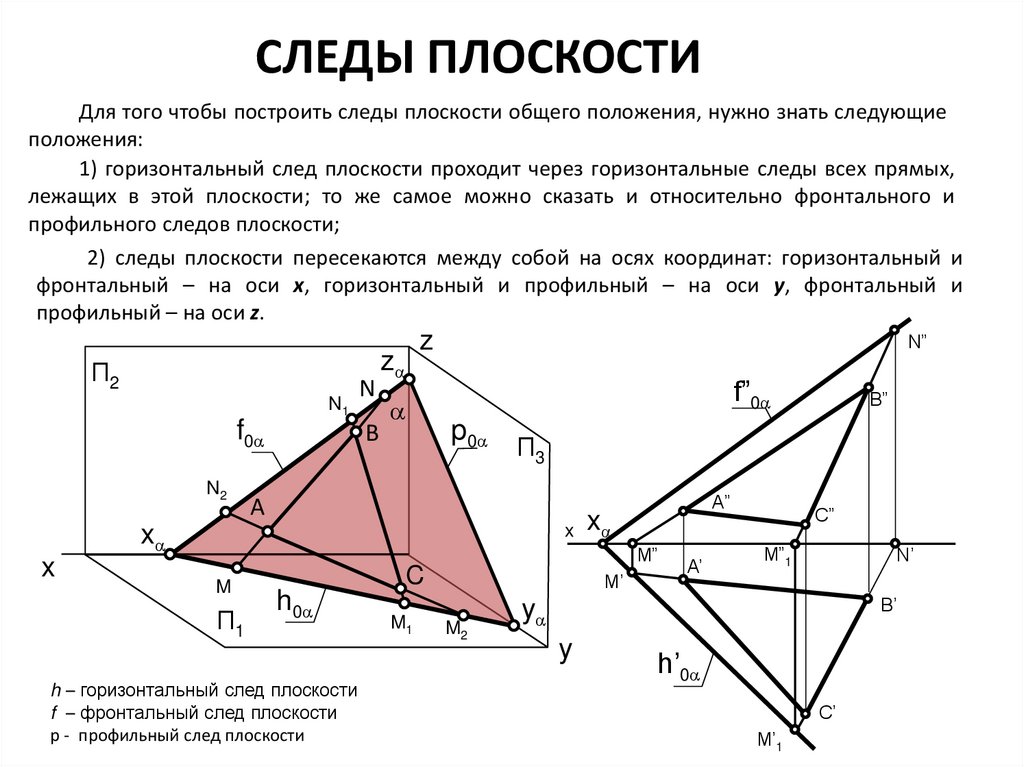
СЛЕДЫ ПЛОСКОСТИ
Для того чтобы построить следы плоскости общего положения, нужно знать следующие
положения:
1) горизонтальный след плоскости проходит через горизонтальные следы всех прямых,
лежащих в этой плоскости; то же самое можно сказать и относительно фронтального и
профильного следов плоскости;
2) следы плоскости пересекаются между собой на осях координат: горизонтальный и
фронтальный – на оси x, горизонтальный и профильный – на оси y, фронтальный и
профильный – на оси z.
П2
N1
f0
N2
N
В
z
z
N”
f”0
p0
П3
А
x
x
x
A”
x
M”
M
П1
C
h0
h – горизонтальный след плоскости
f – фронтальный след плоскости
p - профильный след плоскости
M1
M’
M2
B”
A’
C”
M”1
N’
B’
y
y
h’0
C’
M’1

8.

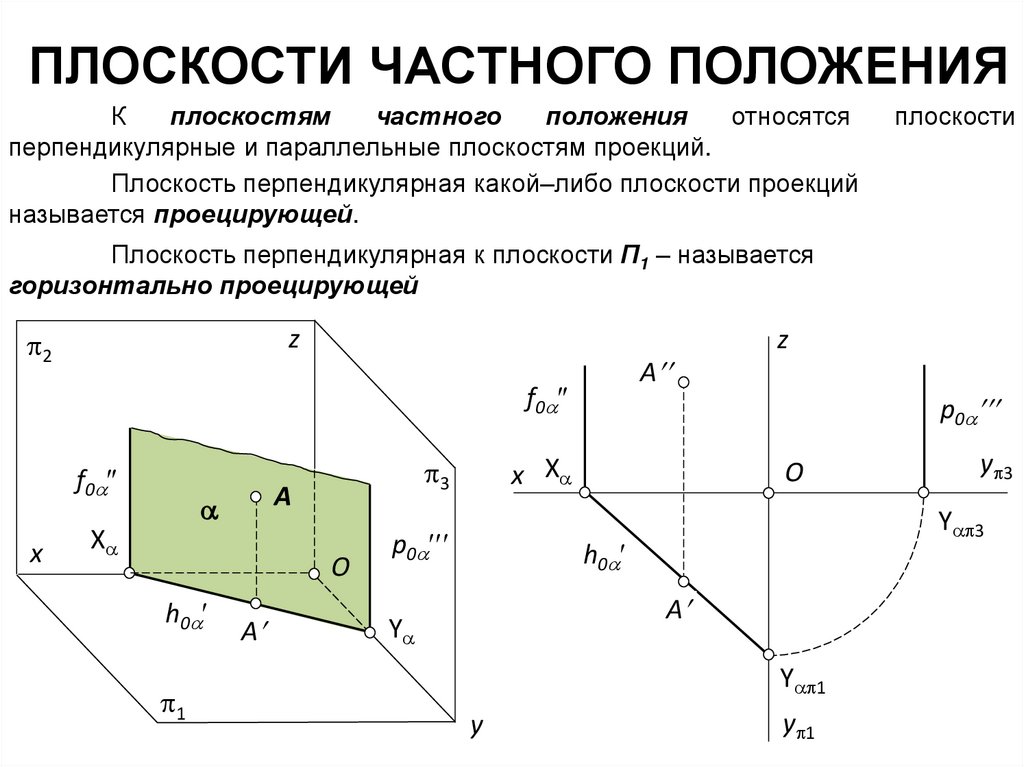
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
К
плоскостям
частного
положения
относятся
перпендикулярные и параллельные плоскостям проекций.
Плоскость перпендикулярная какой–либо плоскости проекций
называется проецирующей.
плоскости
Плоскость перпендикулярная к плоскости П1 – называется
горизонтально проецирующей
z
2
А
f0
f0
x
3
А
X
O
h0
1
А
x X
p0
z
p0
O
Y 3
h0
А
Y
Y 1
y
y 3
y 1

9.

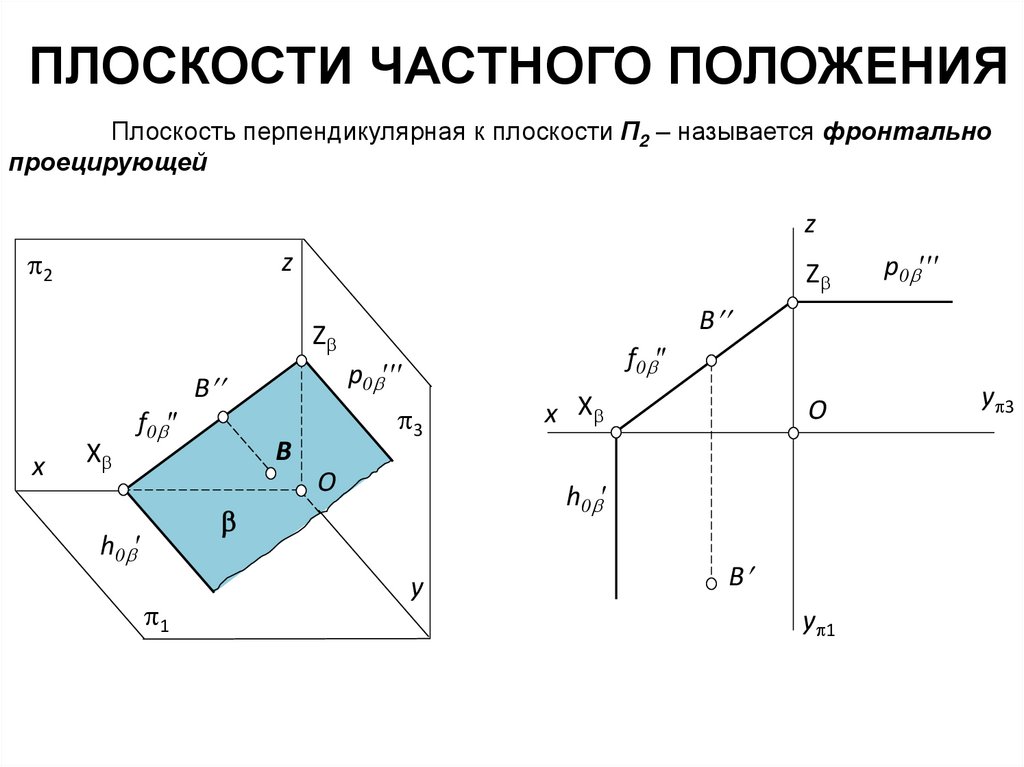
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Плоскость перпендикулярная к плоскости П2 – называется фронтально
проецирующей
z
2
z
Z
Z
x
X
f 0
B
B
f0
p0
3
B
O
1
x X
O
h0
h 0
p0
y
B
y 1
y 3

10.

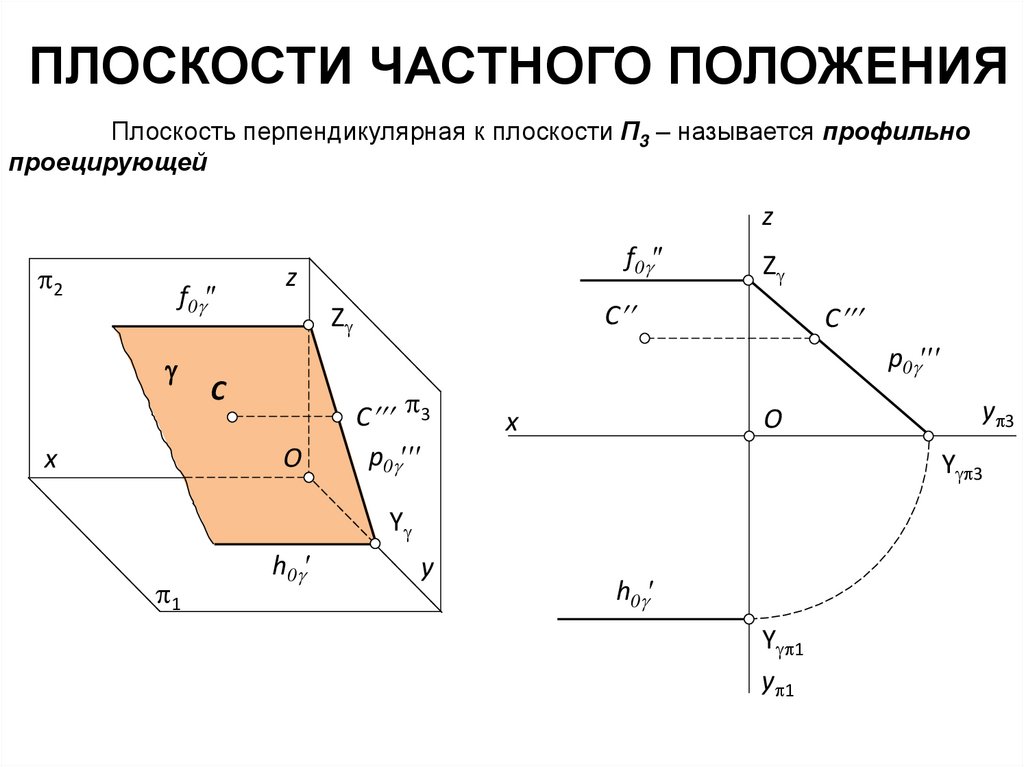
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Плоскость перпендикулярная к плоскости П3 – называется профильно
проецирующей
z
2
f0
z
Z
C
Z
C
p0
С
O
x
f0
С 3
p0
O
x
Y 3
Y
1
h0
y
y 3
h0
Y 1
y 1

11.

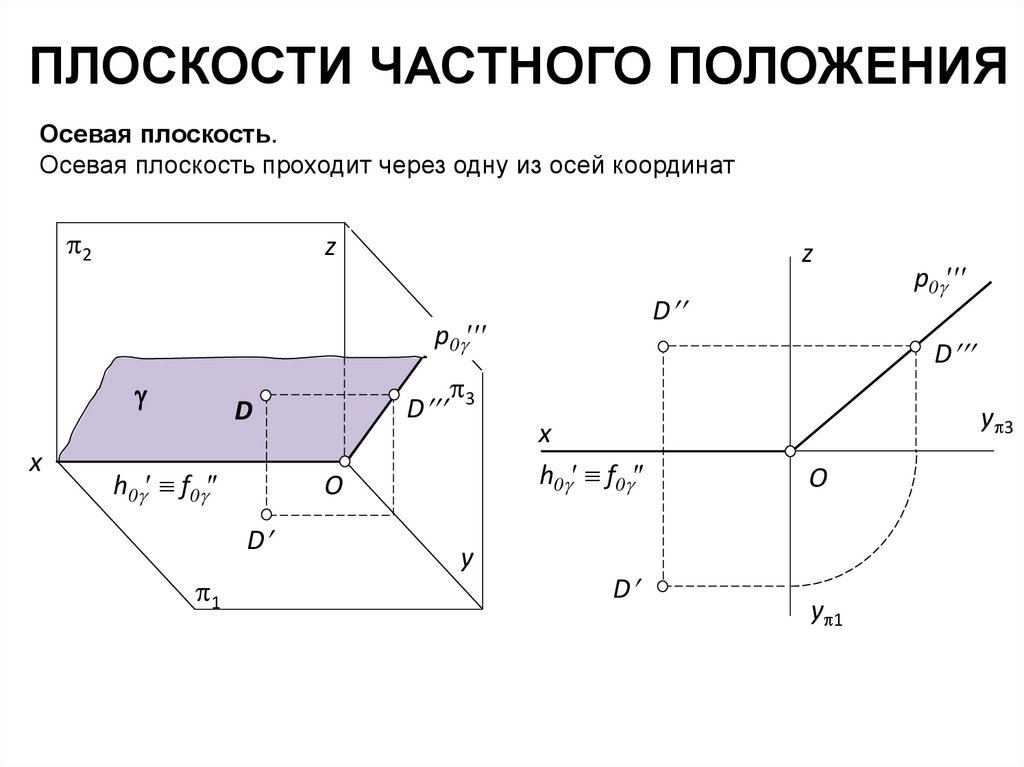
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Осевая плоскость.
Осевая плоскость проходит через одну из осей координат
2
z
z
D
p0
x
D
D
h 0 f0
D
1
D
3
x
h 0 f0
O
y
p0
D
y 3
O
y 1

12.

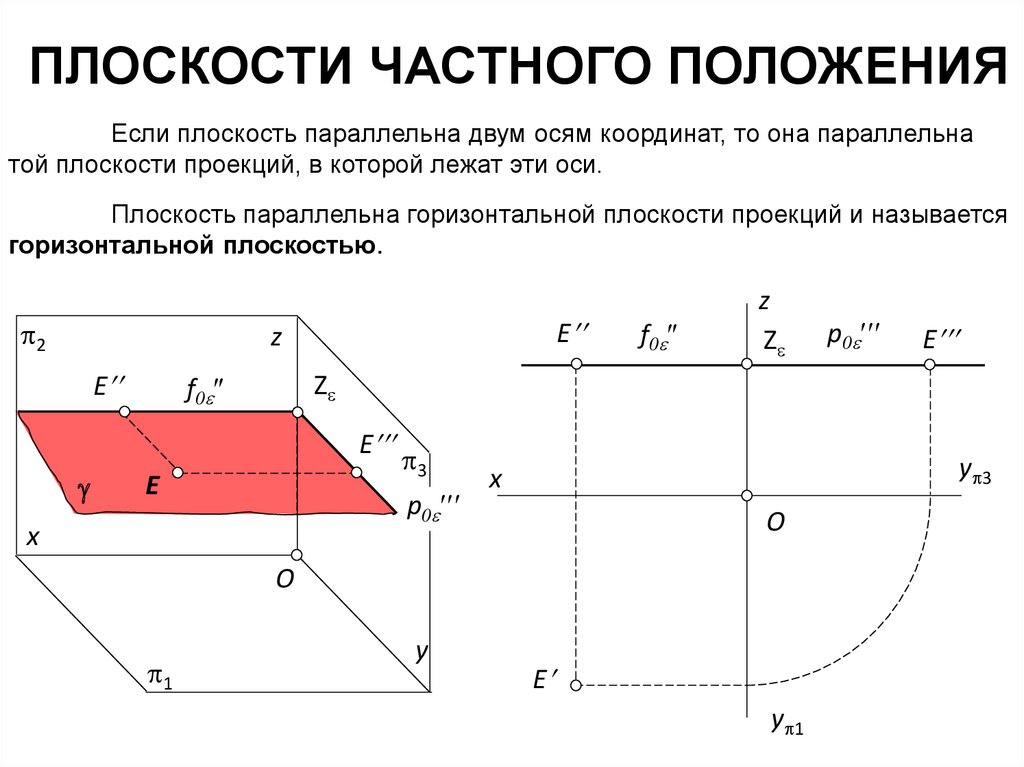
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Если плоскость параллельна двум осям координат, то она параллельна
той плоскости проекций, в которой лежат эти оси.
Плоскость параллельна горизонтальной плоскости проекций и называется
горизонтальной плоскостью.
2
E
z
Е
f0
Е
3
p0
x
E
y 3
x
O
O
1
p0
Z
Е
f0
z
Z
y
E
y 1

13.

ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Аналогичным образом можно построить фронтальную и
профильную
плоскости,
т.е.
плоскости
параллельные
соответственно фронтальной и профильной плоскостям проекций.
Такие плоскости также являются двояко-проецирующими
плоскостями, т.е. перпендикулярными к двум другим плоскостям
проекций.
Все, что лежит в такой плоскости в двух плоскостях проекций (к
которым она перпендикулярна) проецируется на ее следы, а на
третью плоскость проекций (которой она параллельна) – в истинную
величину.