Проекции плоскости

1.

Проекции плоскости

2. Способы задания плоскости

2
1
А2
С2
2
В2
С1
1
А1 В1
(А,В,С)
В2
3
m2
2
m2
4
n2
2
m2
2
n2
В m1
1
1
(В,m)
n1
m1 n1 1
(n m)
m1
1
(n m)
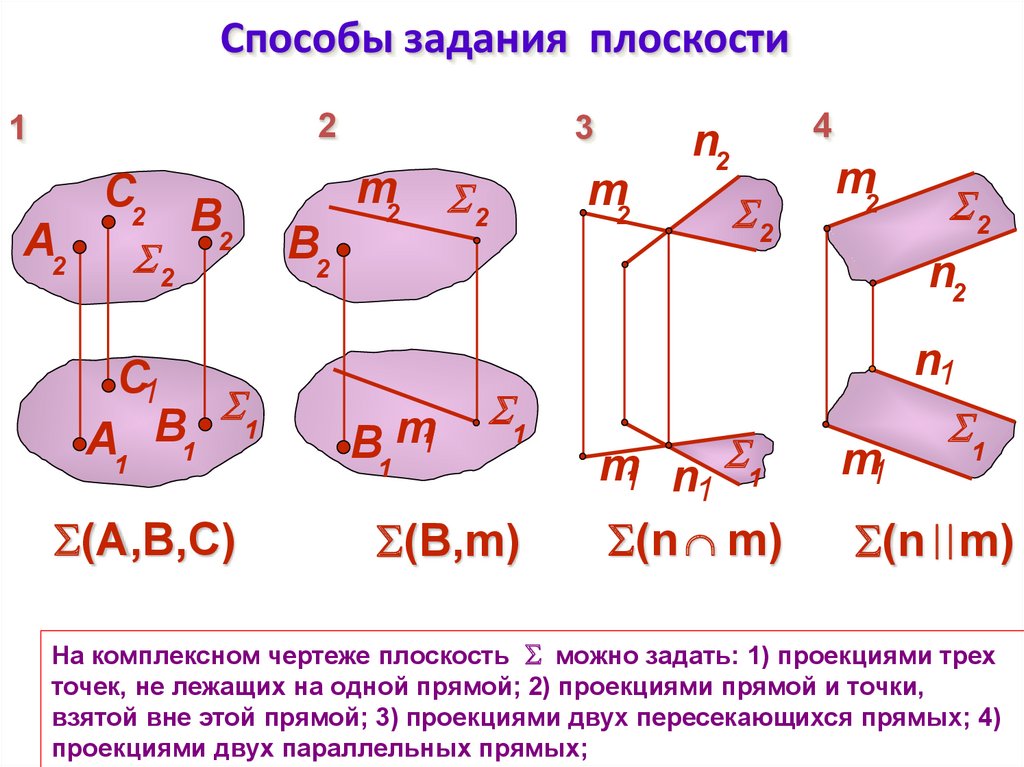
На комплексном чертеже плоскость можно задать: 1) проекциями трех
точек, не лежащих на одной прямой; 2) проекциями прямой и точки,
взятой вне этой прямой; 3) проекциями двух пересекающихся прямых; 4)
проекциями двух параллельных прямых;

3. Способы задания плоскости

5
6
С2
x
С1
1
( АВС)
В1
z
П2
2 В2
А2
А1
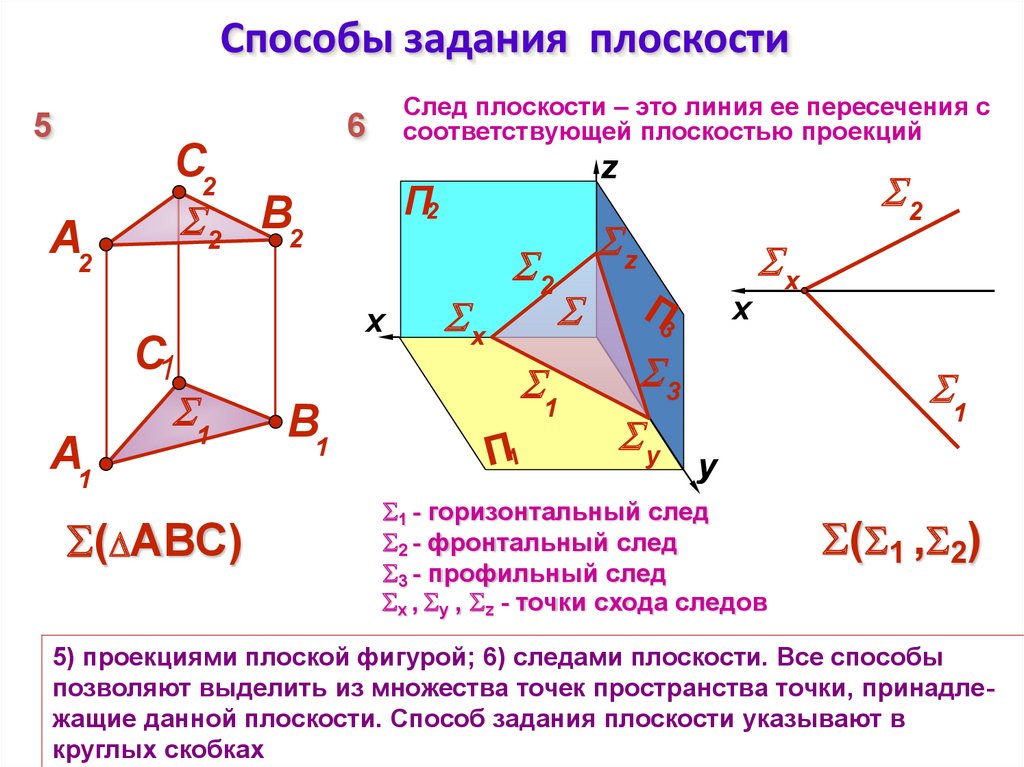
След плоскости – это линия ее пересечения с
соответствующей плоскостью проекций
х
2
2
z
1
x
х
3
y
1
y
1 - горизонтальный след
2 - фронтальный след
3 - профильный след
x , y , z - точки схода следов
( 1 , 2)
5) проекциями плоской фигурой; 6) следами плоскости. Все способы
позволяют выделить из множества точек пространства точки, принадлежащие данной плоскости. Способ задания плоскости указывают в
круглых скобках

4. Положение плоскости относительно плоскостей проекций

Плоскость общего положения наклонена ко всем
плоскостям проекций
Плоскость частного положения перпендикулярна
или параллельна одной из плоскостей проекций
Плоскость, перпендикулярная одной из плоскостей
проекций, называется проецирующей плоскостью:
Горизонтально проецирующая плоскость
П1
Фронтально проецирующая плоскость
П2
Профильно
проецирующая
П3
Плоскость,
параллельная
плоскостиплоскость
проекций, назы-
вается плоскостью уровня (дважды проецирующей):
Горизонтальная плоскость П1
Фронтальная плоскость
П2
Профильная плоскость
П3

5. Горизонтально проецирующая плоскость (П1)

Горизонтально проецирующая плоскость ( П1)
Пространственная картина
z
Комплексный чертеж
2
П2
2
x
х
1
В2
А2
C2
3
y
y
x
х
А1
В1
C1
1
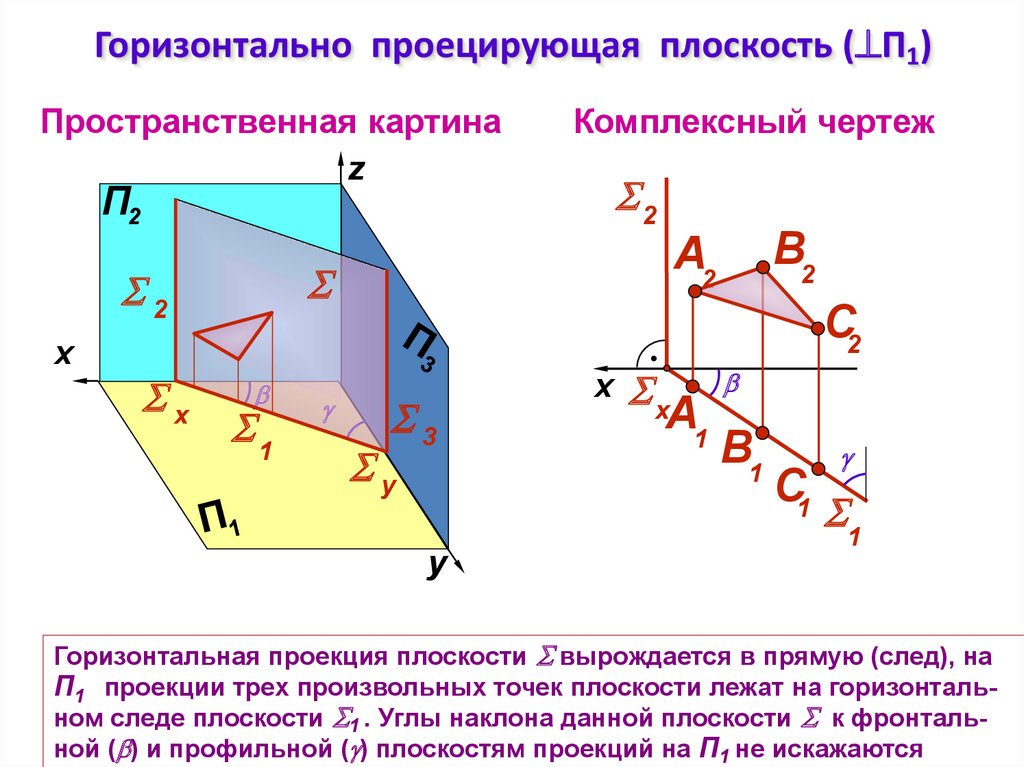
Горизонтальная проекция плоскости вырождается в прямую (след), на
П1 проекции трех произвольных точек плоскости лежат на горизонтальном следе плоскости 1 . Углы наклона данной плоскости к фронтальной ( ) и профильной ( ) плоскостям проекций на П1 не искажаются

6. Фронтально проецирующая плоскость (П2)

Фронтально проецирующая плоскость ( П2)
Пространственная картина
z
Комплексный чертеж
П2
x
х
1
2
z
3
y
x
х
А2
В2
C2
2
C1
1
А1
В1
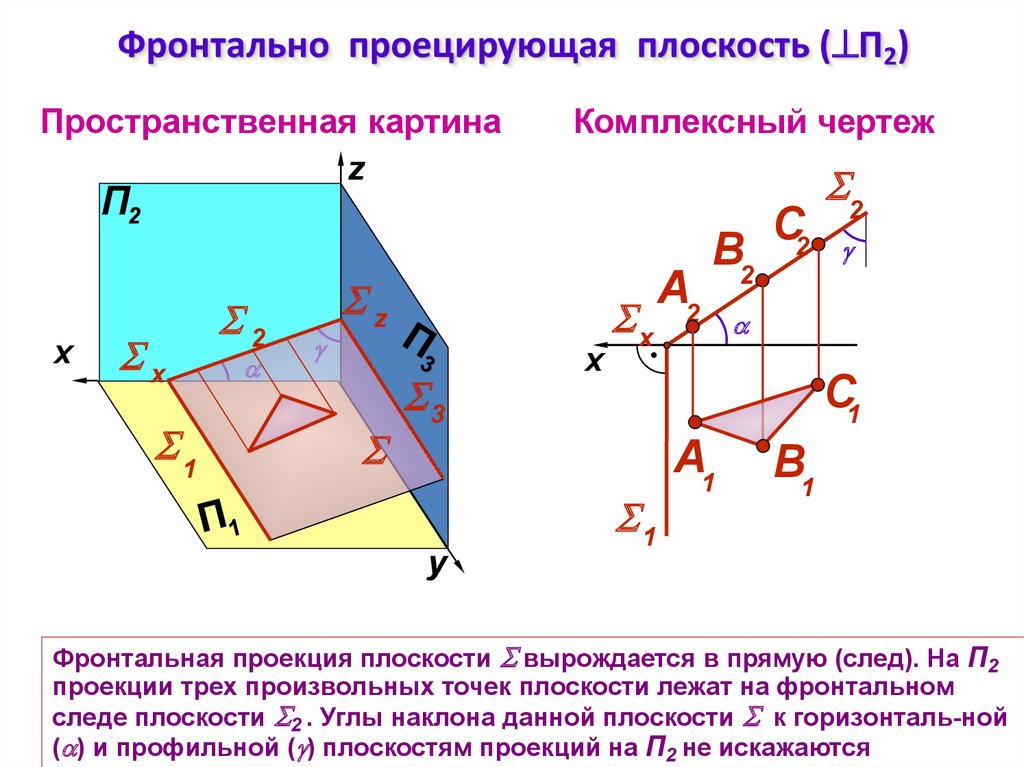
Фронтальная проекция плоскости вырождается в прямую (след). На П2
проекции трех произвольных точек плоскости лежат на фронтальном
следе плоскости 2 . Углы наклона данной плоскости к горизонталь-ной
( ) и профильной ( ) плоскостям проекций на П2 не искажаются

7. Профильно проецирующая плоскость (П3)

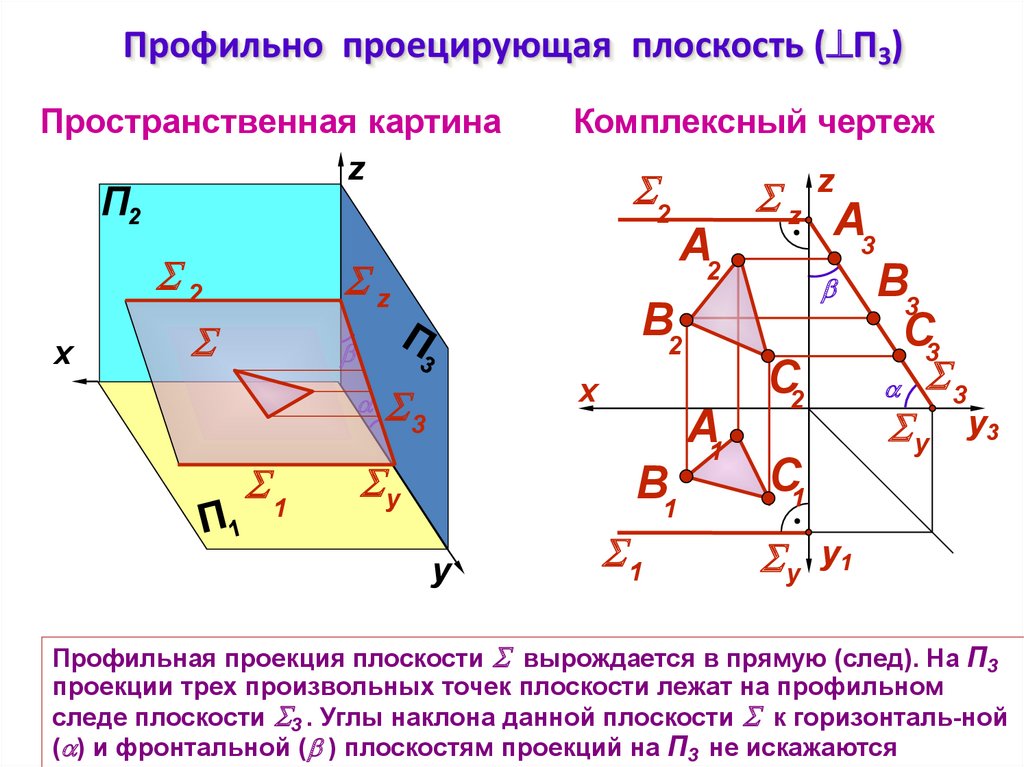
Профильно проецирующая плоскость ( П3)
Пространственная картина
z
Комплексный чертеж
2
П2
2
x
z
1
x
3
y
В1
y
1
А1
А3
В2
А2
z
z
C2
В3
C3
3
y y3
C1
y y1
Профильная проекция плоскости вырождается в прямую (след). На П3
проекции трех произвольных точек плоскости лежат на профильном
следе плоскости 3 . Углы наклона данной плоскости к горизонталь-ной
( ) и фронтальной ( ) плоскостям проекций на П3 не искажаются

8. Горизонтальная плоскость уровня ( П1)

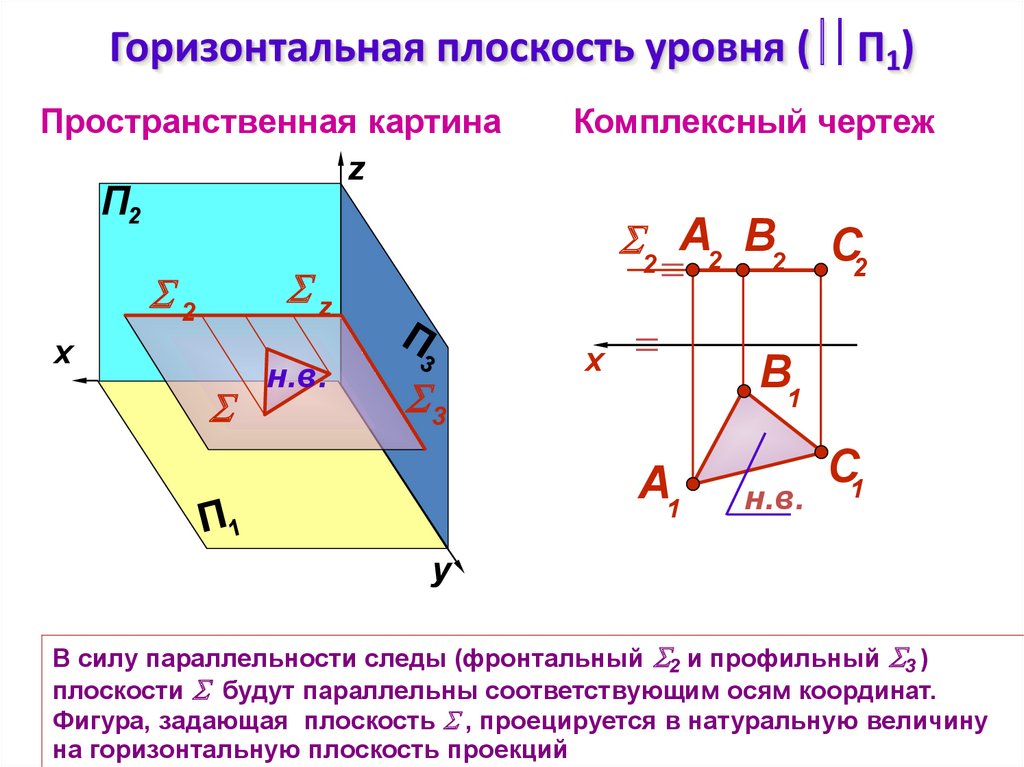
Горизонтальная плоскость уровня ( П1)
Пространственная картина
z
Комплексный чертеж
П2
2 А2 В2
z
2
x
н.в.
3
x
C2
В1
А1
н.в.
C1
y
В силу параллельности следы (фронтальный 2 и профильный 3 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , проецируется в натуральную величину
на горизонтальную плоскость проекций

9. Фронтальная плоскость уровня ( П2)

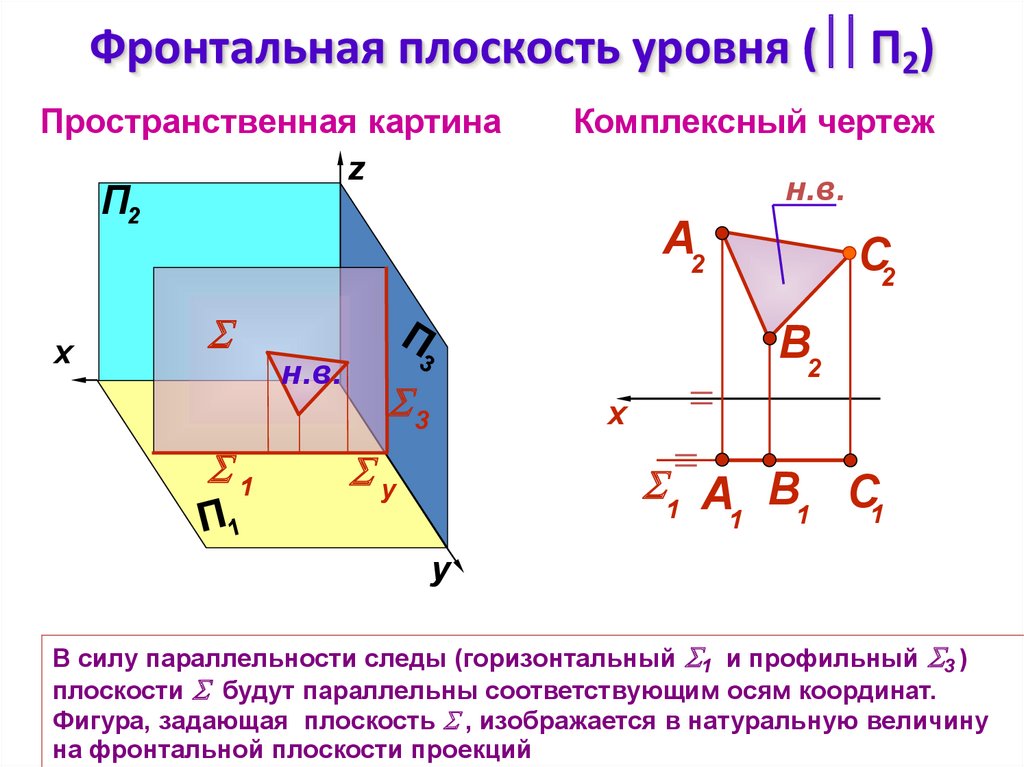
Фронтальная плоскость уровня ( П2)
Пространственная картина
z
Комплексный чертеж
н.в.
П2
x
А2
1
н.в.
C2
В2
3
x
y
1 А В C
1
1
1
y
В силу параллельности следы (горизонтальный 1 и профильный 3 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , изображается в натуральную величину
на фронтальной плоскости проекций

10. Профильная плоскость уровня ( П3)

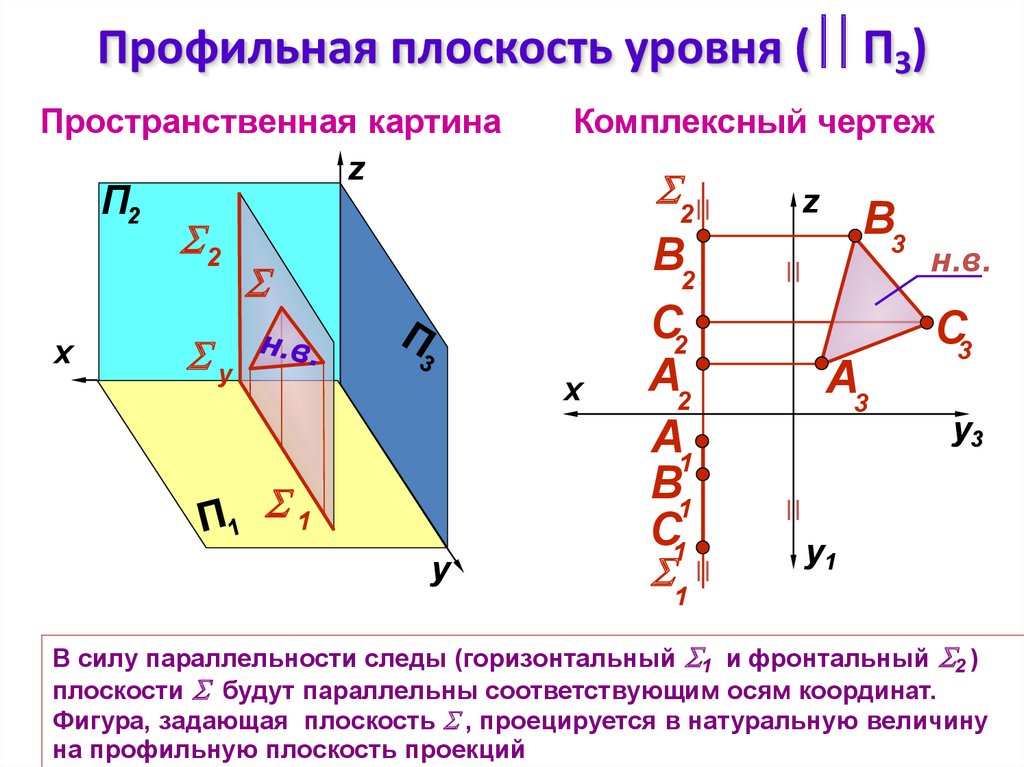
Профильная плоскость уровня ( П3)
Пространственная картина
z
П2
x
2
Комплексный чертеж
2
y
x
1
y
В2
C2
А2
А1
В1
C1
1
z
В3
А3
н.в.
C3
y3
y1
В силу параллельности следы (горизонтальный 1 и фронтальный 2 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , проецируется в натуральную величину
на профильную плоскость проекций

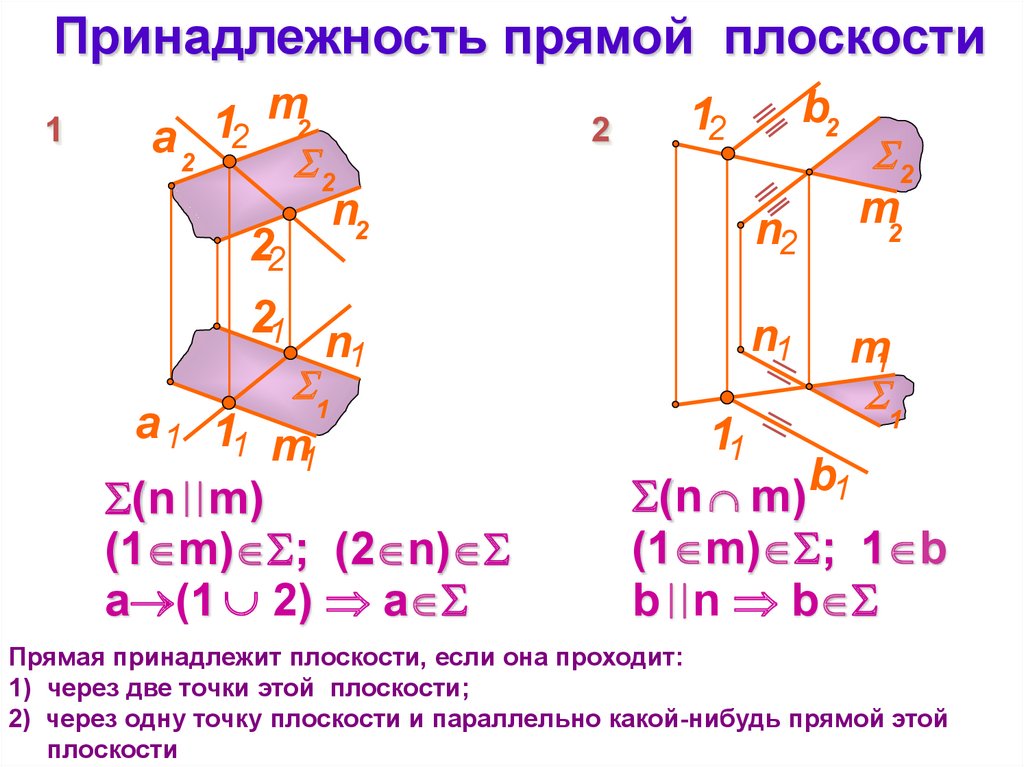
11. Принадлежность прямой плоскости

1
m2
1
а2 2
2
2
n2
n2
m2
n1
n1
m1
22
21
2
b2
12
1
а 1 11 m
1
(n m)
(1 m) ; (2 n)
а (1 2) а
11
1
(n m) b1
(1 m) ; 1 b
b n b
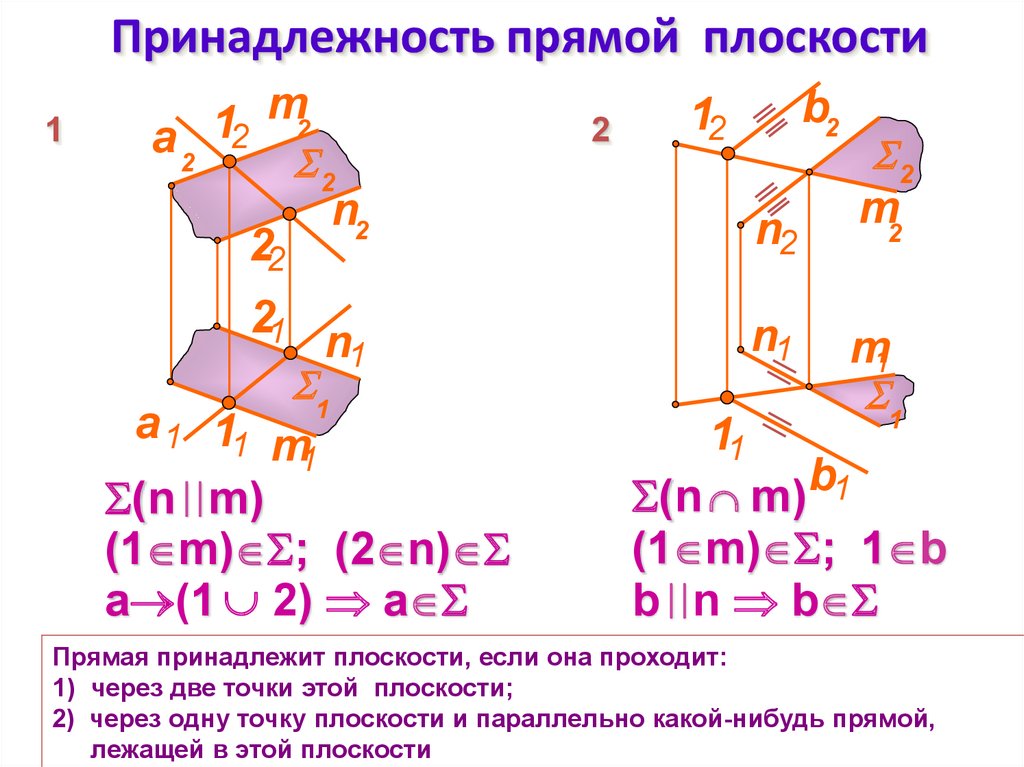
Прямая принадлежит плоскости, если она проходит:
1) через две точки этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой,
лежащей в этой плоскости

12. Принадлежность точки плоскости

12
А2
2
1
D2
32
22
11
А1
С2
1
( АВС)
(1 АС)
2
В2
С1 2
1 3
1
D1
В1
1,2 - ?
2
D2 - ?, если D
П1: (D1 A1) С1В1
П321: 32 C2B2
=
А2 32
D2 А232
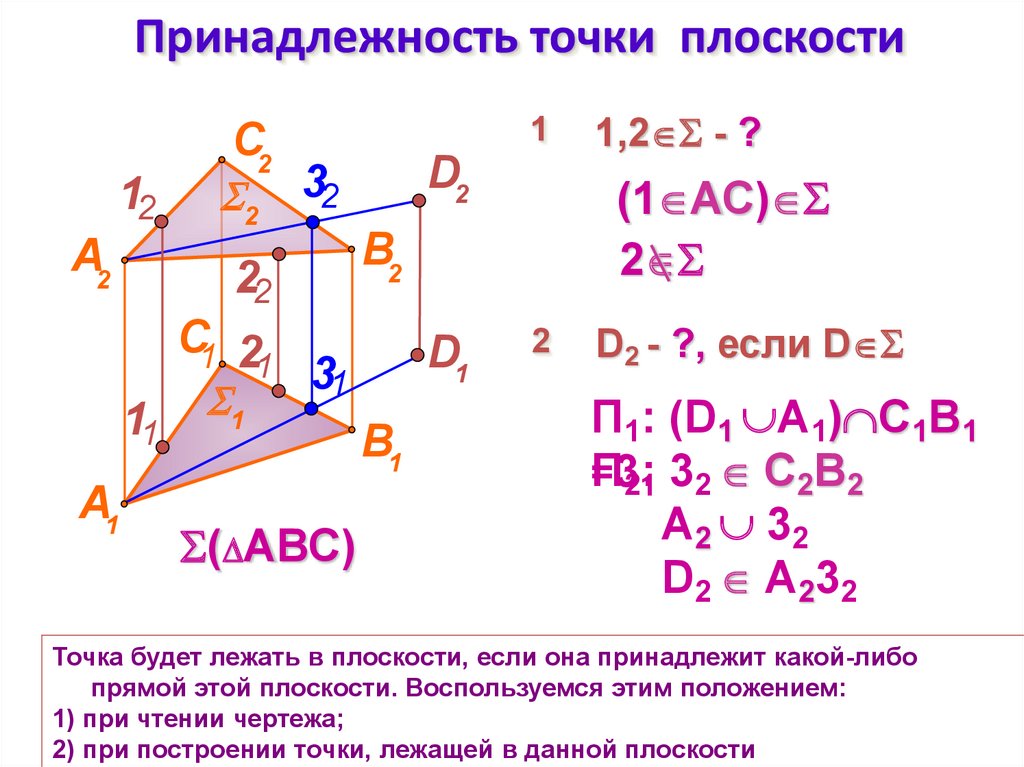
Точка будет лежать в плоскости, если она принадлежит какой-либо
прямой этой плоскости. Воспользуемся этим положением:
1) при чтении чертежа;
2) при построении точки, лежащей в данной плоскости

13. Принадлежность прямой и точки плоскости

К2 2А
2
2 А2 М2
x
х
В2
N2
А1
х
x
М1
1
N1
П1
A1 1 А
N1M1 1 MN
К1 А1
В1
1
П2
К2 2 К
А2В2 2 АВ
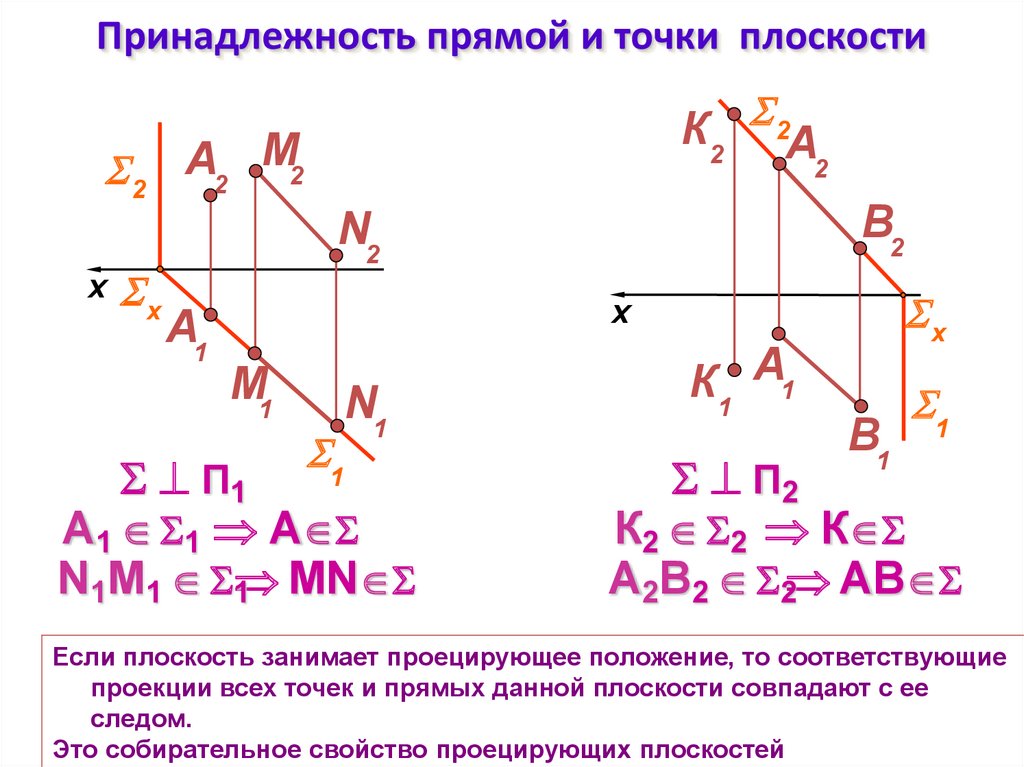
Если плоскость занимает проецирующее положение, то соответствующие
проекции всех точек и прямых данной плоскости совпадают с ее
следом.
Это собирательное свойство проецирующих плоскостей

14.

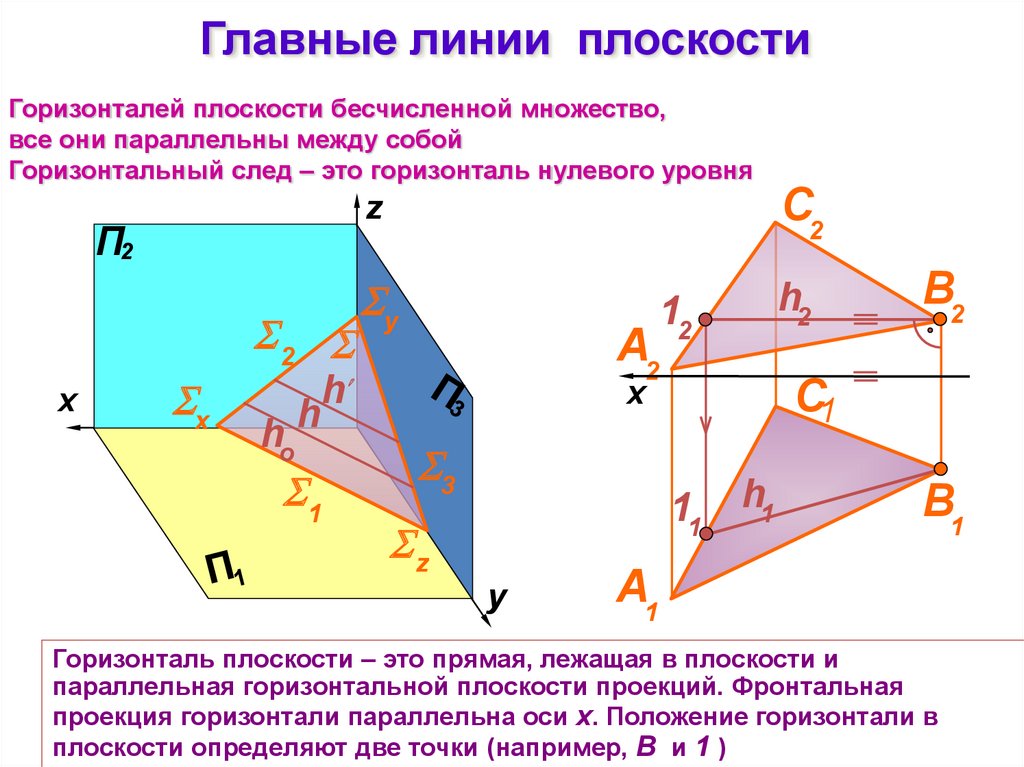
Главные линии плоскости
Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня
П2
2
x
х
hh
o
z
С2
y
h2
А2
h
1
12
С1
x
3
11 h1
z
y
В2
В1
А1
Горизонталь плоскости – это прямая, лежащая в плоскости и
параллельная горизонтальной плоскости проекций. Фронтальная
проекция горизонтали параллельна оси x. Положение горизонтали в
плоскости определяют две точки (например, В и 1 )

15.

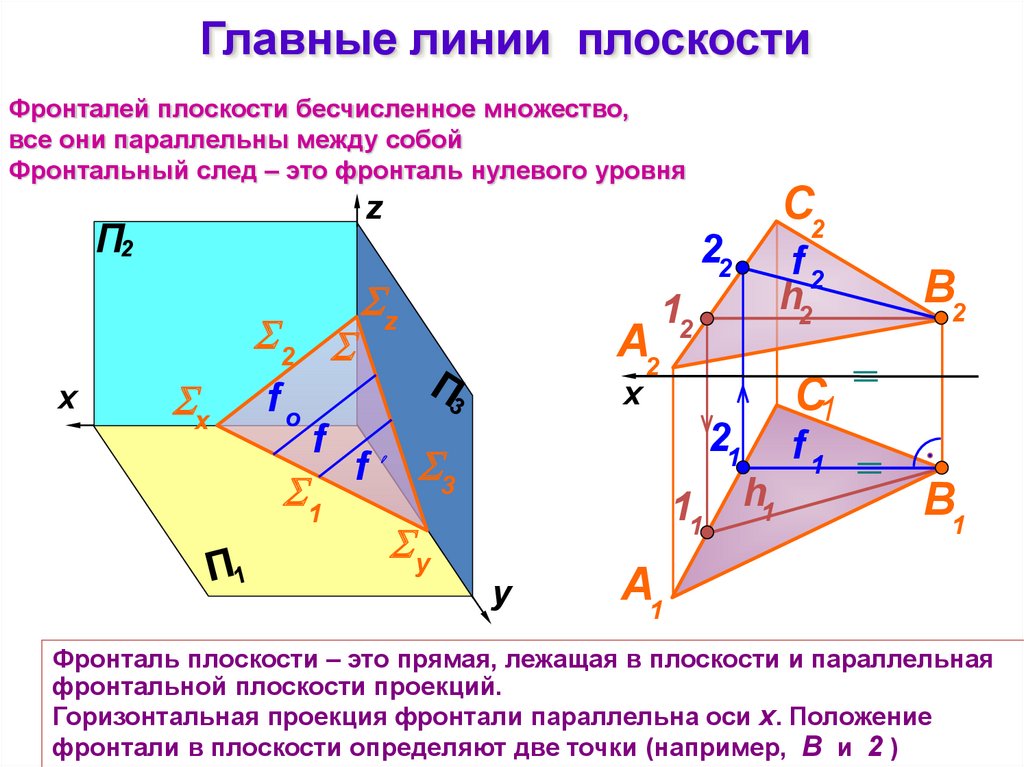
Главные линии плоскости
Фронталей плоскости бесчисленное множество,
все они параллельны между собой
Фронтальный след – это фронталь нулевого уровня
z
П2
2
x
х
fo
22
z
А2
12
x
f
1
f
21
3
11 h1
y
y
С2
f2
h2
В2
С1
f1
В1
А1
Фронталь плоскости – это прямая, лежащая в плоскости и параллельная
фронтальной плоскости проекций.
Горизонтальная проекция фронтали параллельна оси x. Положение
фронтали в плоскости определяют две точки (например, В и 2 )

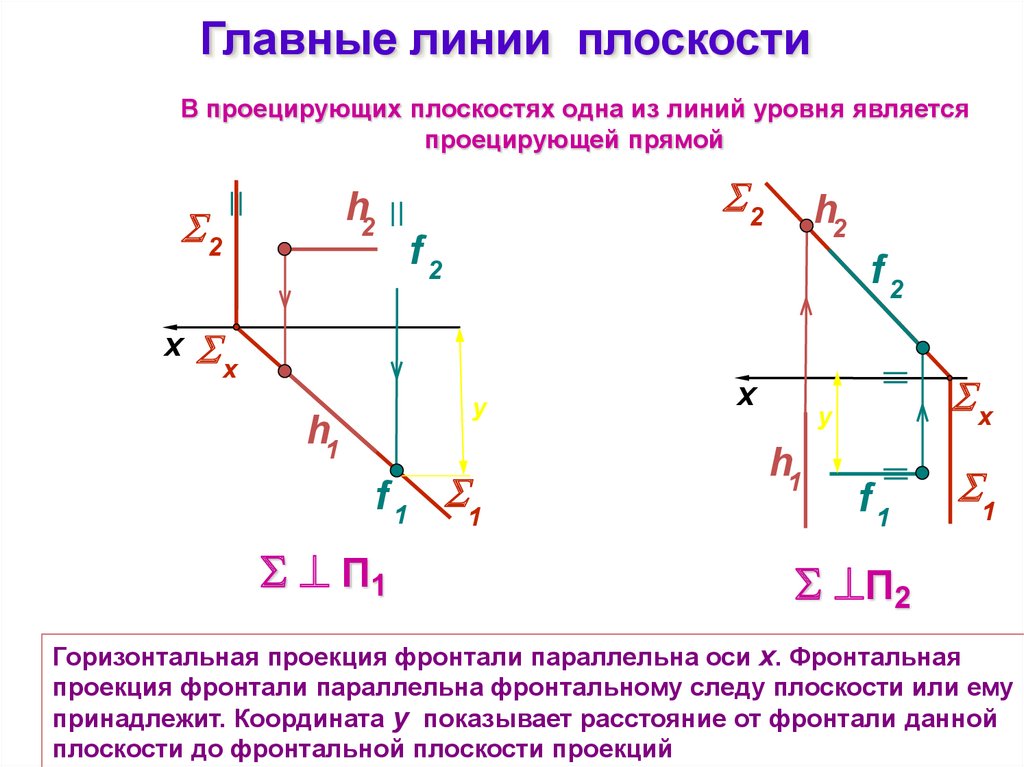
16.

Главные линии плоскости
В проецирующих плоскостях одна из линий уровня является
проецирующей прямой
h2
2
x
2
f2
f2
х
y
h1
f 1 1
П1
h2
x
х
y
h1
f1
1
П2
Горизонтальная проекция фронтали параллельна оси x. Фронтальная
проекция фронтали параллельна фронтальному следу плоскости или ему
принадлежит. Координата y показывает расстояние от фронтали данной
плоскости до фронтальной плоскости проекций

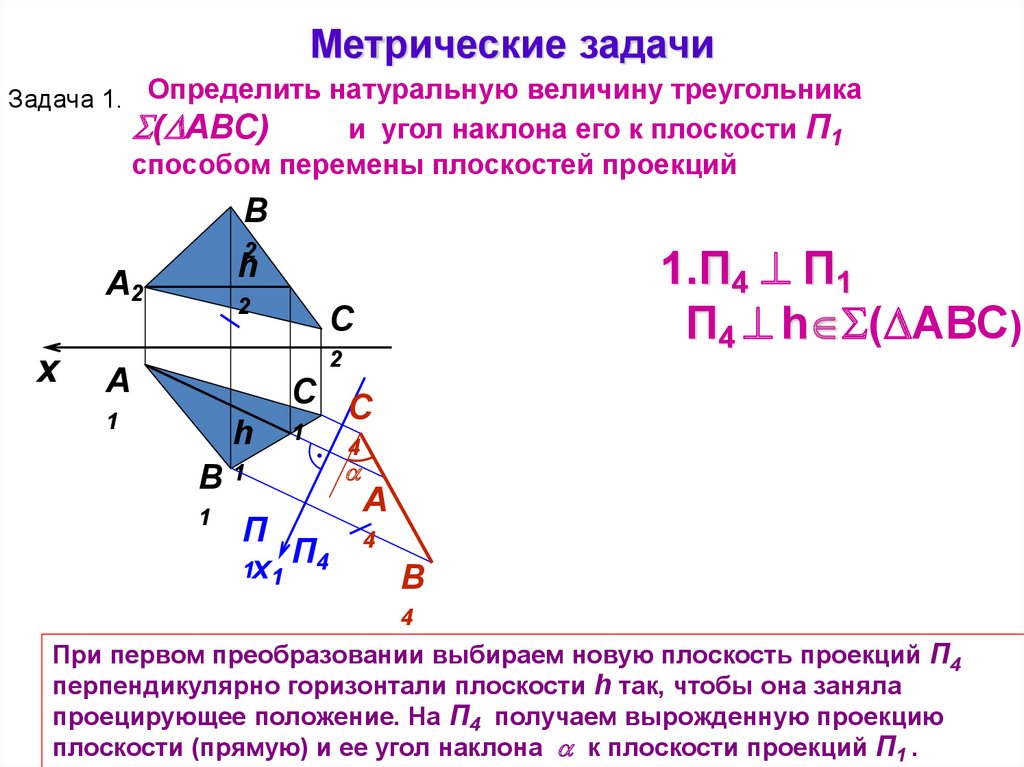
17.

Метрические задачи
Задача 1. Определить натуральную величину треугольника
( АВС)
и угол наклона его к плоскости П1
способом перемены плоскостей проекций
B
1.П4 П1
П4 h ( АВС)
2
h
А2
x
2
C
2
А
1
h
C C
1
B1
1
П
П
1x1 4
4
А
4
В
4
При первом преобразовании выбираем новую плоскость проекций П4
перпендикулярно горизонтали плоскости h так, чтобы она заняла
проецирующее положение. На П4 получаем вырожденную проекцию
плоскости (прямую) и ее угол наклона к плоскости проекций П1 .

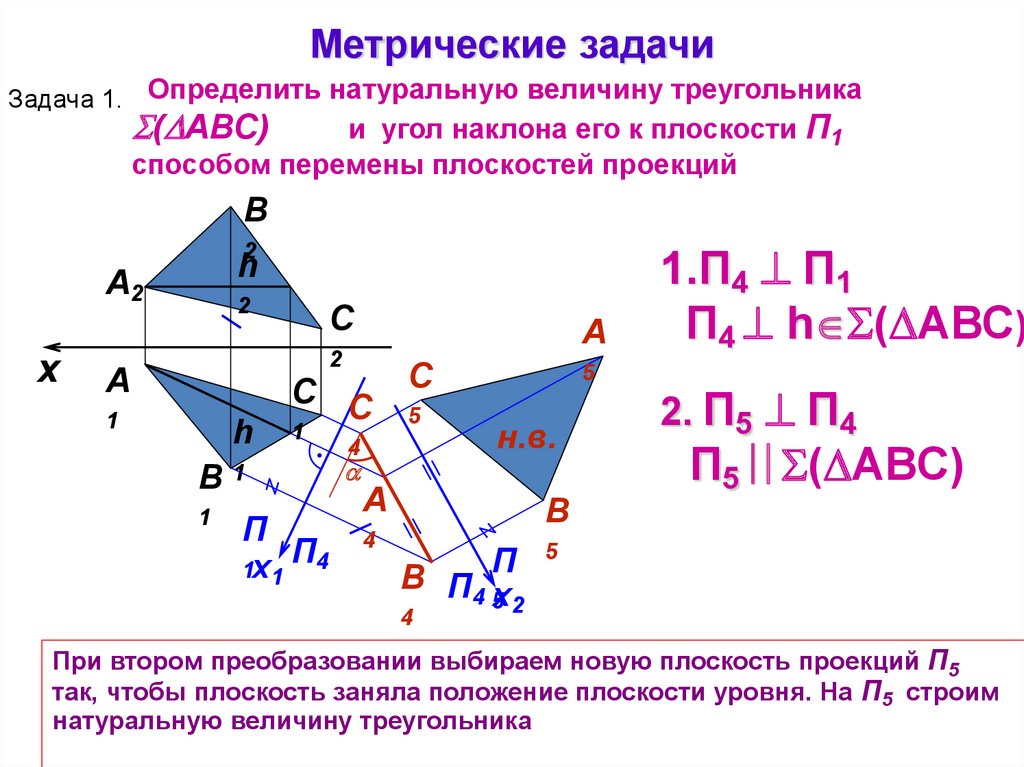
18.

Метрические задачи
Задача 1. Определить натуральную величину треугольника
( АВС)
и угол наклона его к плоскости П1
способом перемены плоскостей проекций
B
2
h
А2
x
2
C
А
2
А
1
h
C C
1
B1
1
П
П
1x1 4
C
5
4
5
н.в.
А
4
В
В П4 П
x2
5
1.П4 П1
П4 h ( АВС)
2. П5 П4
П5 ( АВС)
5
4
При втором преобразовании выбираем новую плоскость проекций П5
так, чтобы плоскость заняла положение плоскости уровня. На П5 строим
натуральную величину треугольника

19.

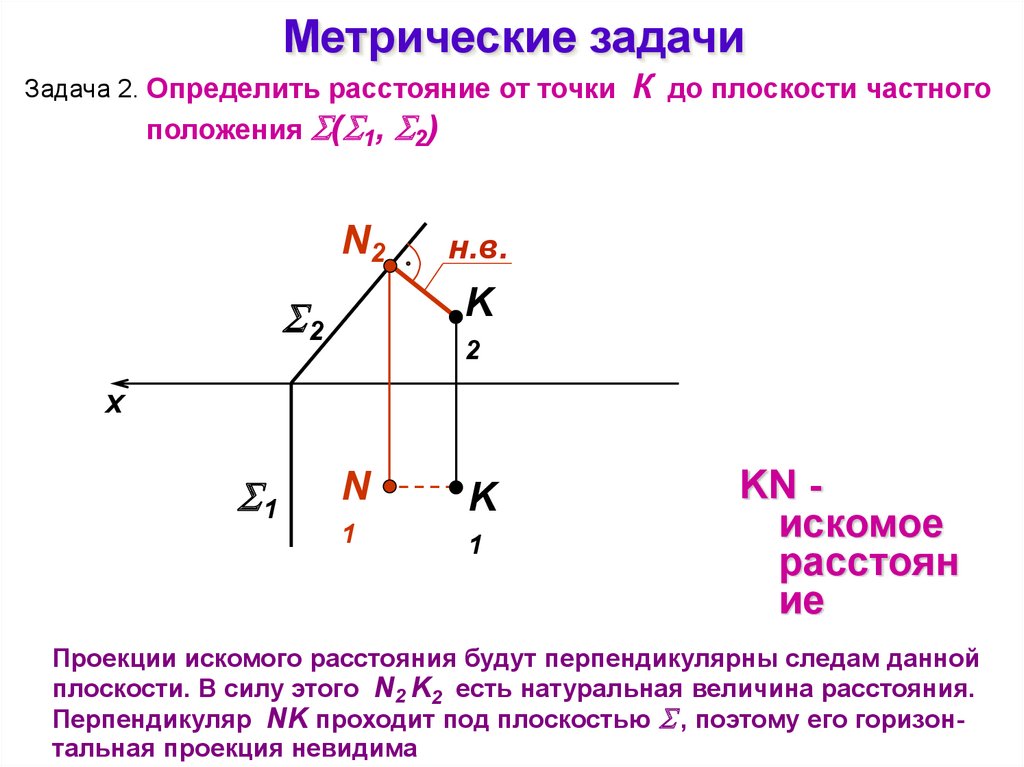
Метрические задачи
Задача 2. Определить расстояние от точки
положения ( 1,
N2
2)
К до плоскости частного
н.в.
K
2
2
x
1
N
K
1
1
KN искомое
расстоян
ие
Проекции искомого расстояния будут перпендикулярны следам данной
плоскости. В силу этого N2 K2 есть натуральная величина расстояния.
Перпендикуляр NK проходит под плоскостью , поэтому его горизонтальная проекция невидима

20.

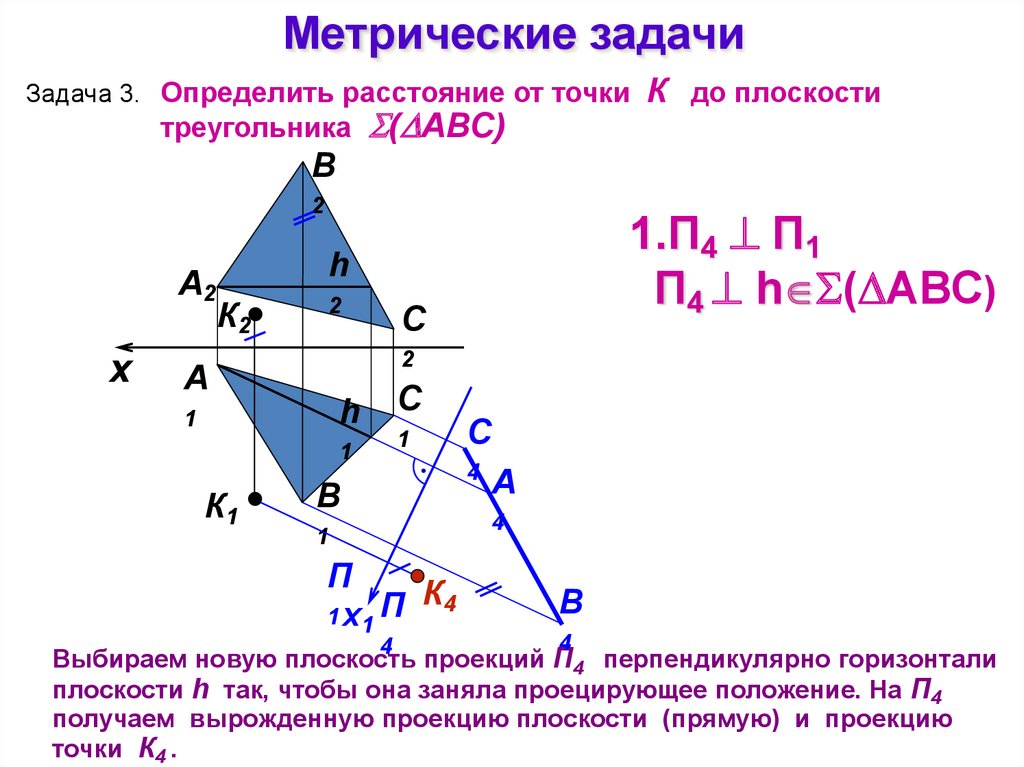
Метрические задачи
Задача 3. Определить расстояние от точки
треугольника
( АВС)
К до плоскости
B
2
А2
x
1.П4 П1
П4 h ( АВС)
h
К2
2
C
2
А
C
h
1
1
1
К1
C
4
B
А
4
1
П
К4
1 x1 П
4
В
4
Выбираем новую плоскость проекций П4 перпендикулярно горизонтали
плоскости h так, чтобы она заняла проецирующее положение. На П4
получаем вырожденную проекцию плоскости (прямую) и проекцию
точки К4 .

21.

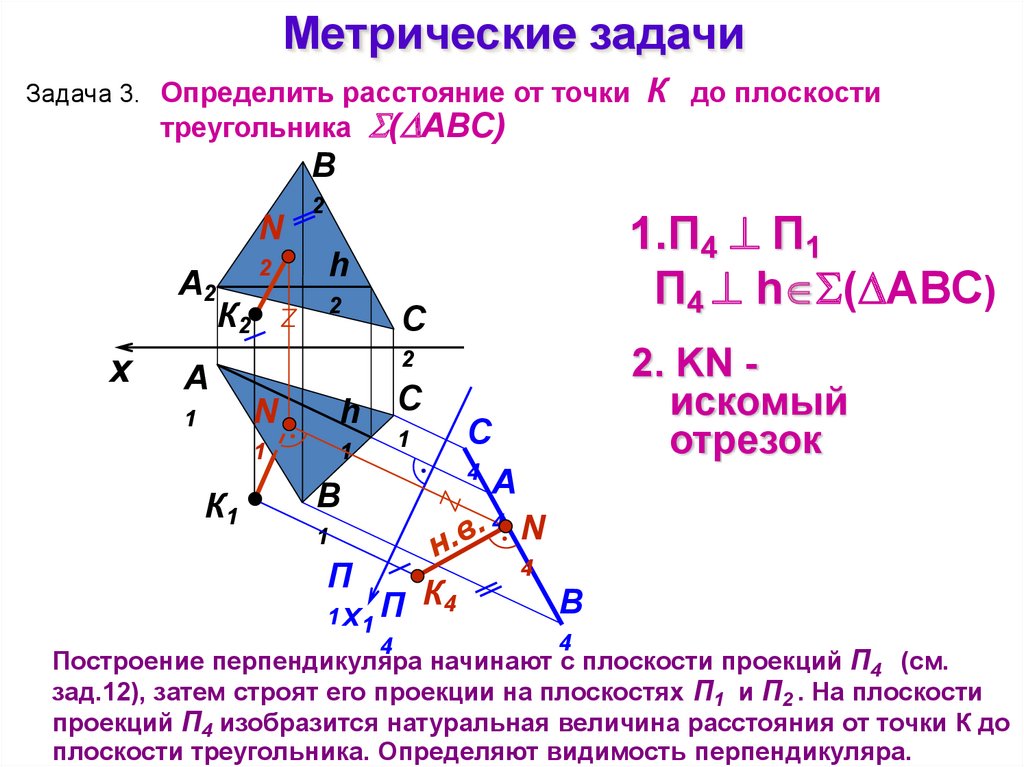
Метрические задачи
Задача 3. Определить расстояние от точки
треугольника
( АВС)
К до плоскости
B
N
А2
x
2
К2
2
h
2
C
К1
2. KN искомый
отрезок
2
А
1
1.П4 П1
П4 h ( АВС)
N
h
1
1
C
1
C
4
B
А
4
1
П
К4
1 x1 П
4
N
4
В
4
Построение перпендикуляра начинают с плоскости проекций П4 (см.
зад.12), затем строят его проекции на плоскостях П1 и П2 . На плоскости
проекций П4 изобразится натуральная величина расстояния от точки К до
плоскости треугольника. Определяют видимость перпендикуляра.

22.

Взаимное положение прямой и
плоскости, двух плоскостей.
Позиционные задачи

23. Взаимное положение прямой и плоскости, двух плоскостей

Прямая и плоскость:
• Прямая принадлежит плоскости (см. тема 3): все точки
прямой являются точками плоскости
• Прямая параллельна плоскости: общих точек нет
• Прямая пересекает плоскость: одна общая точка
Две плоскости:
• Плоскости параллельны: общих прямых нет
• Плоскости пересекаются: одна общая прямая

24.

Принадлежность прямой плоскости
1
m2
1
а2 2
2
2
n2
n2
m2
n1
n1
m1
22
21
2
b2
12
1
а 1 11 m
1
(n m)
(1 m) ; (2 n)
а (1 2) а
11
1
(n m) b1
(1 m) ; 1 b
b n b
Прямая принадлежит плоскости, если она проходит:
1) через две точки этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой этой
плоскости

25.

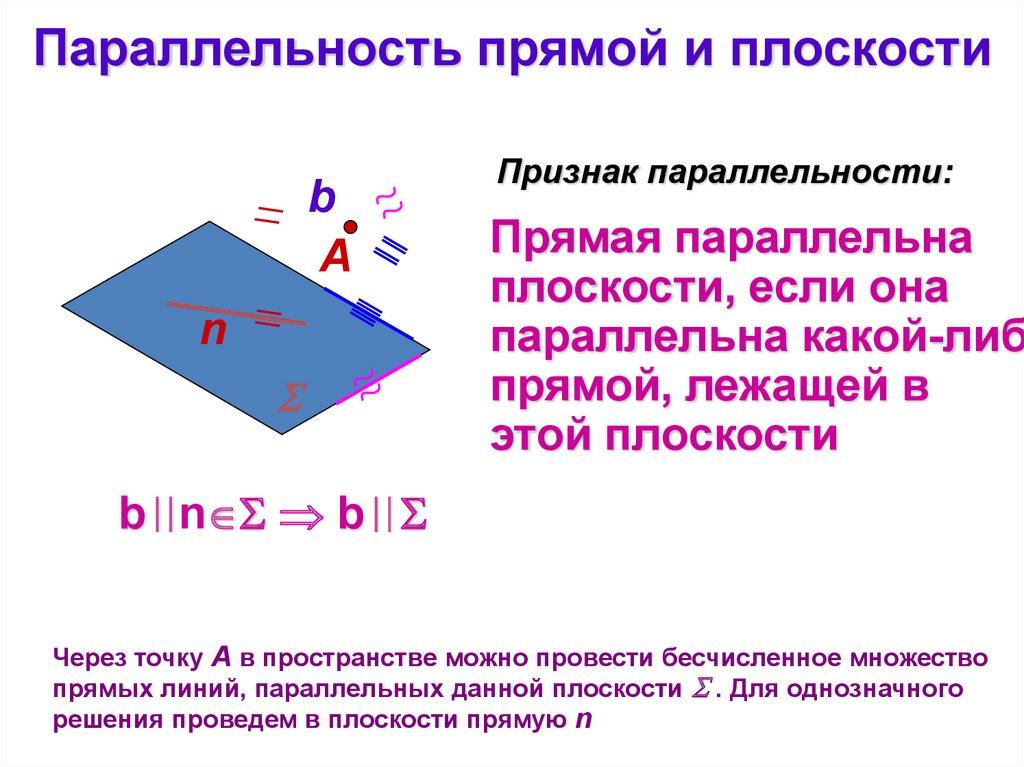
Параллельность прямой и плоскости
b
А
n
Признак параллельности:
Прямая параллельна
плоскости, если она
параллельна какой-либ
прямой, лежащей в
этой плоскости
b n b
Через точку А в пространстве можно провести бесчисленное множество
прямых линий, параллельных данной плоскости . Для однозначного
решения проведем в плоскости прямую n

26. Параллельность прямой и плоскости

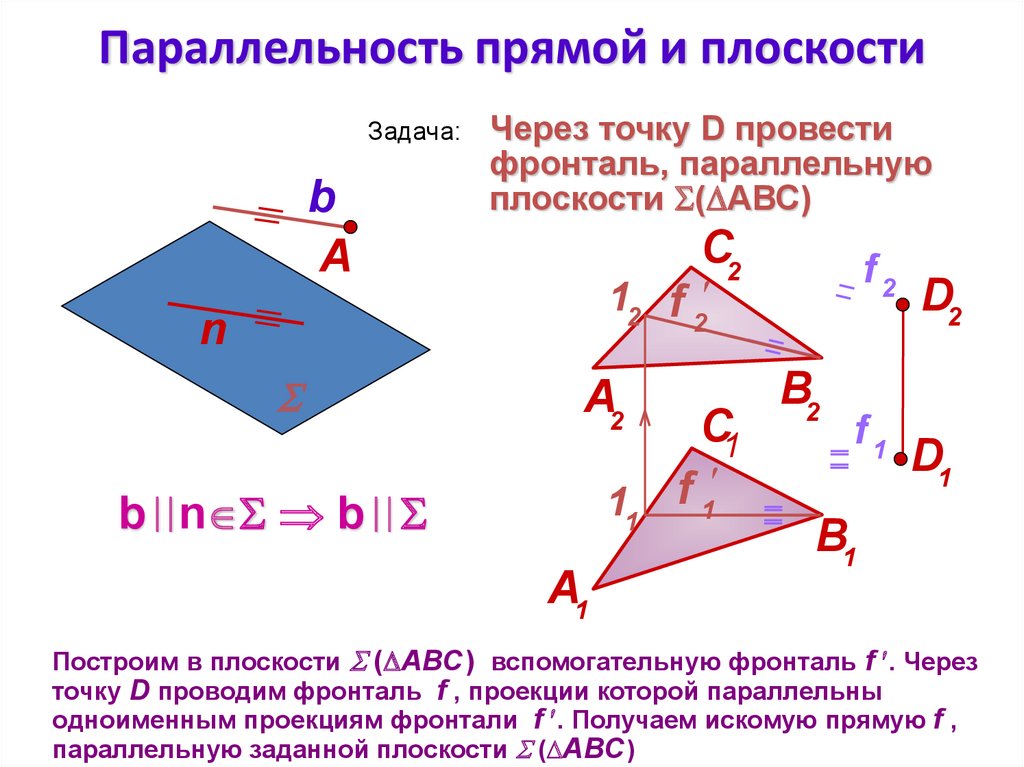
Задача:
b
А
Через точку D провести
фронталь, параллельную
плоскости ( АВС)
С2
12 f
2
n
f2
А2
b n b
11
А1
С1
f 1
В2
f1
D2
D1
В1
Построим в плоскости ( АВС ) вспомогательную фронталь f . Через
точку D проводим фронталь f , проекции которой параллельны
одноименным проекциям фронтали f . Получаем искомую прямую f ,
параллельную заданной плоскости ( АВС )

27.

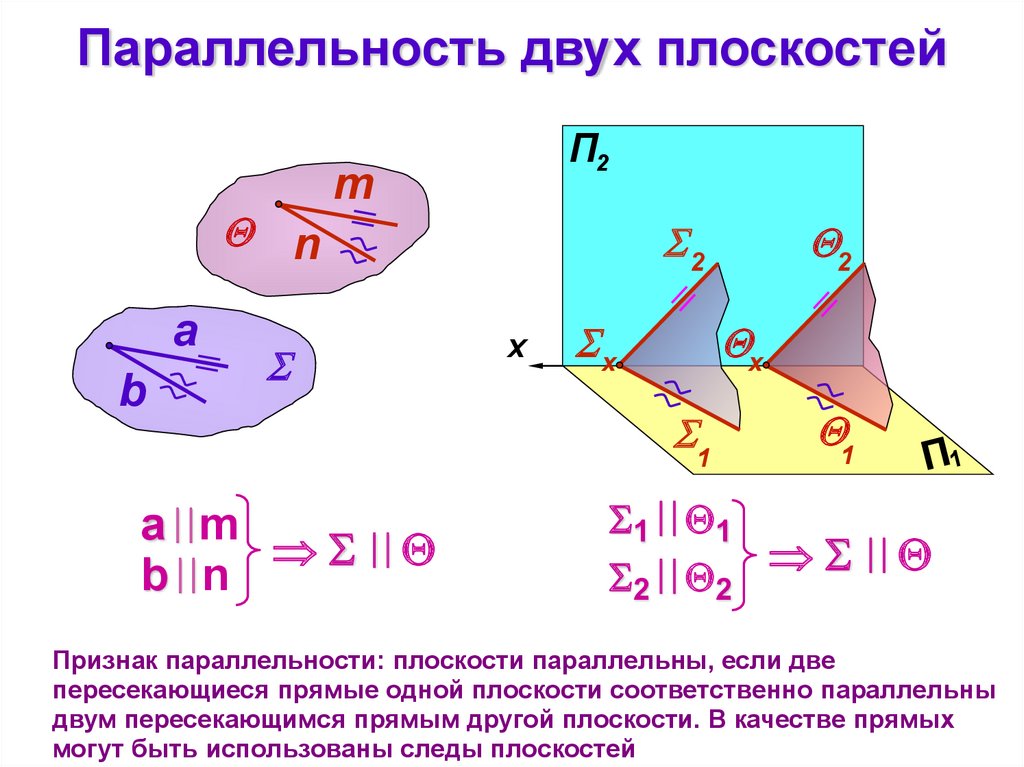
Параллельность двух плоскостей
n
a
b
П2
m
а m
b n
2
x
х
2
х
1
1
1 1
2 2
Признак параллельности: плоскости параллельны, если две
пересекающиеся прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости. В качестве прямых
могут быть использованы следы плоскостей

28.

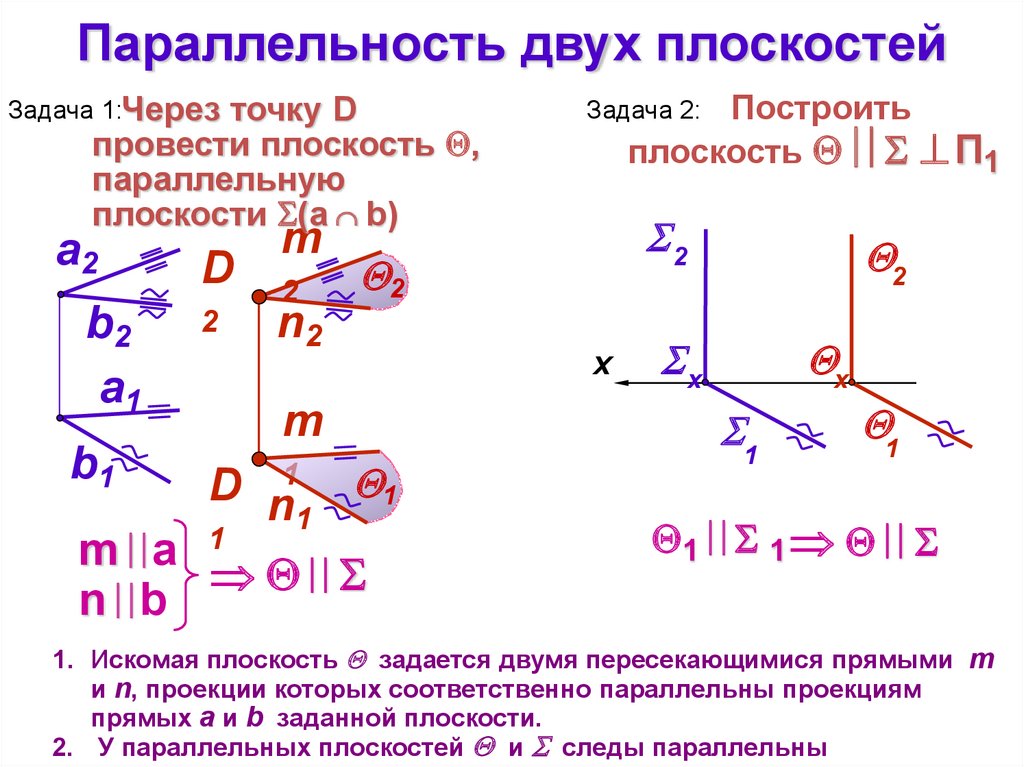
Параллельность двух плоскостей
Задача 1:Через
точку D
провести плоскость ,
параллельную
плоскости (a b)
a2
b2
a1
b1
D
2
m
2
Построить
плоскость П1
Задача 2:
2
2
n2
m
D n1 1
1
m a 1
n b
x
2
х
х
1
1
1 1
1. Искомая плоскость задается двумя пересекающимися прямыми m
и n, проекции которых соответственно параллельны проекциям
прямых а и b заданной плоскости.
2. У параллельных плоскостей и следы параллельны

29.

Пересечение прямой с проецирующей
плоскостью
П2
2
x
х
1
2
n
2
n 1
n 11
1
2
1 n
2
x
1
2
х
n
11
1
1
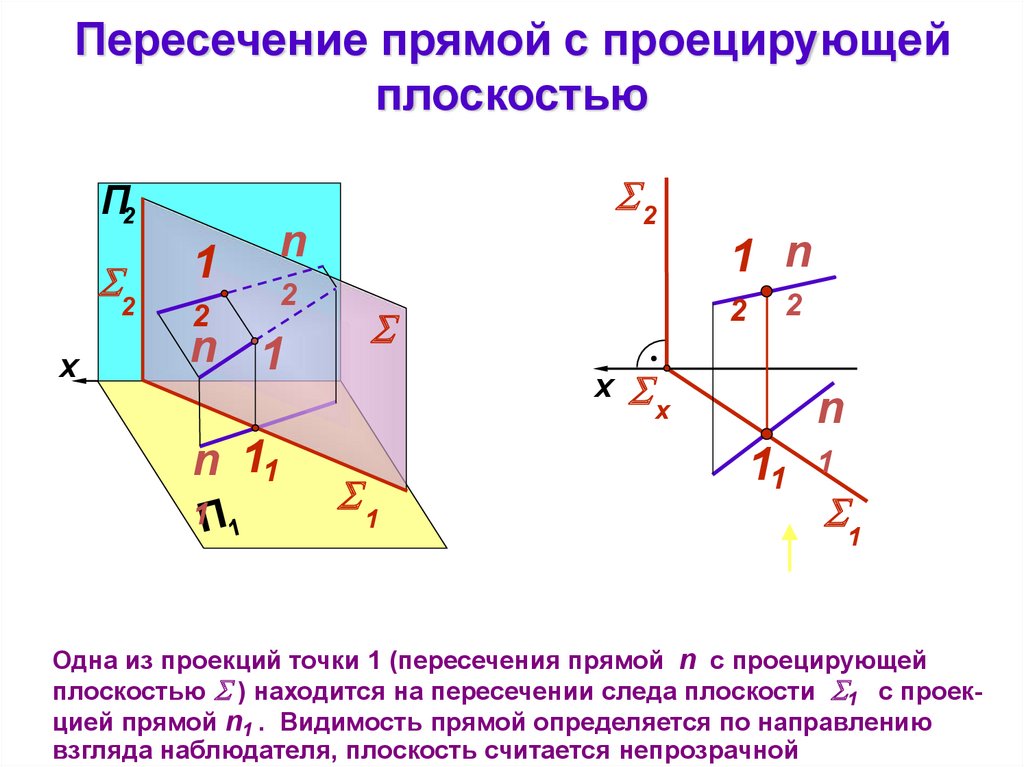
Одна из проекций точки 1 (пересечения прямой n с проецирующей
плоскостью ) находится на пересечении следа плоскости 1 с проекцией прямой n1 . Видимость прямой определяется по направлению
взгляда наблюдателя, плоскость считается непрозрачной

30.

Пересечение плоскости общего
положения с проецирующей плоскостью
2
П2
22
2
x х
12
1
2
1
21
11
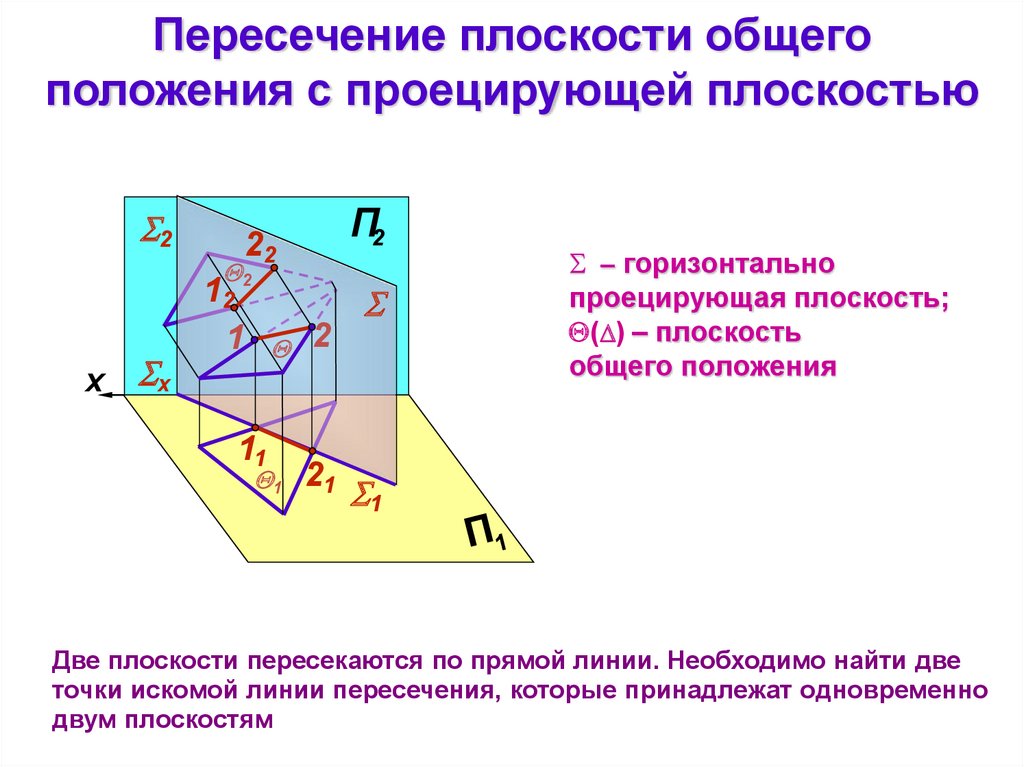
– горизонтально
проецирующая плоскость;
( ) – плоскость
общего положения
1
Две плоскости пересекаются по прямой линии. Необходимо найти две
точки искомой линии пересечения, которые принадлежат одновременно
двум плоскостям

31.

Пересечение плоскости общего
положения с проецирующей плоскостью
2
x х
П2
22
12
1
11
2
В
2
2
12
1
С
2
x
В
21
А 22
С
11
1
1
21
1
А
1
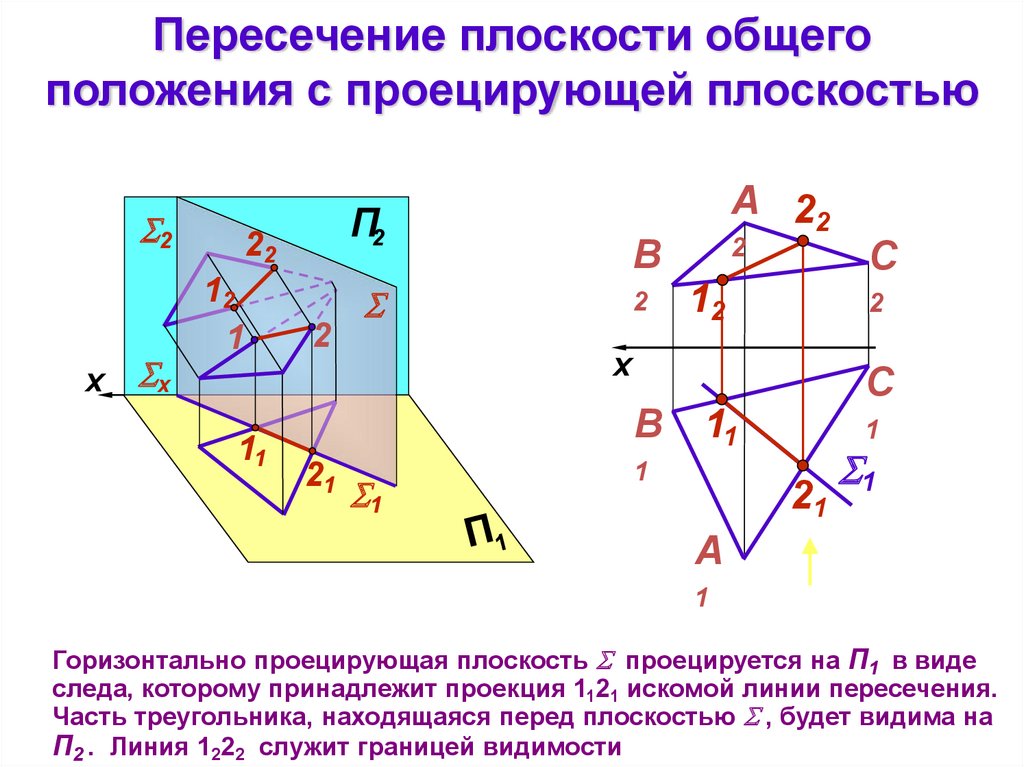
Горизонтально проецирующая плоскость проецируется на П1 в виде
следа, которому принадлежит проекция 1121 искомой линии пересечения.
Часть треугольника, находящаяся перед плоскостью , будет видима на
П2 . Линия 1222 служит границей видимости

32.

Пересечение прямой общего положения
с плоскостью общего положения
m
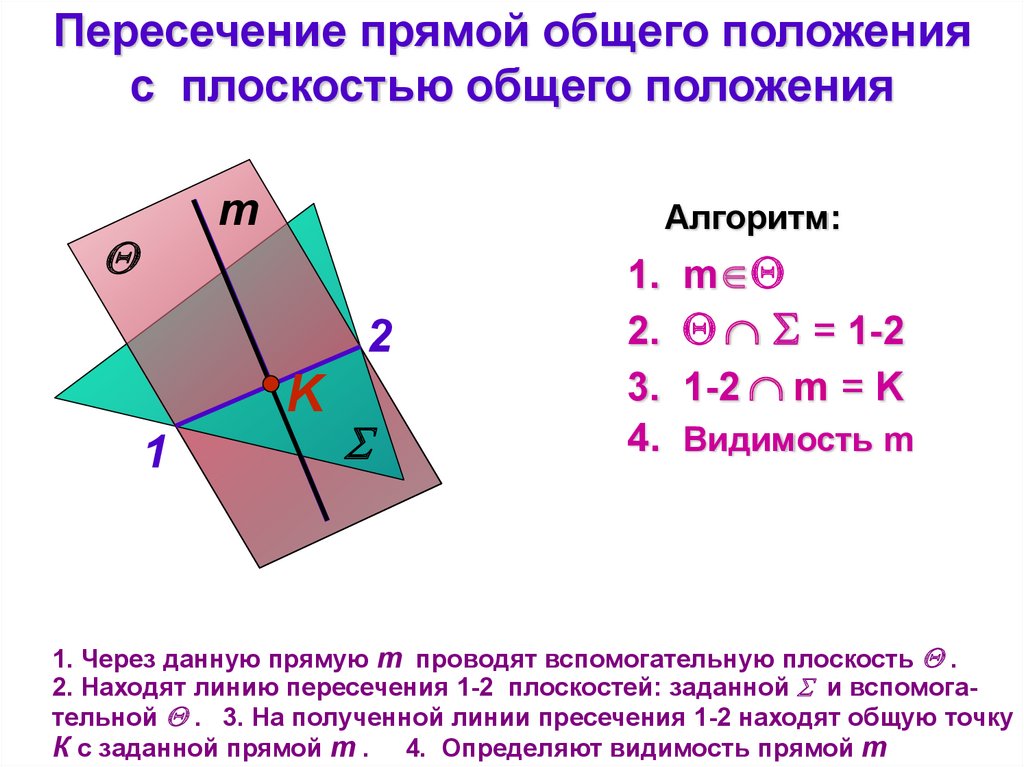
Алгоритм:
2
K
1
1.
2.
3.
4.
m
= 1-2
1-2 m = K
Видимость m
1. Через данную прямую m проводят вспомогательную плоскость .
2. Находят линию пересечения 1-2 плоскостей: заданной и вспомогательной . 3. На полученной линии пресечения 1-2 находят общую точку
К с заданной прямой m . 4. Определяют видимость прямой m

33.

Пересечение прямой общего положения с
плоскостью общего положения
12
m2
2
22
21
11
1. m ;
П1 1 m1
2. ( )=1-2;
1121 1222
m1
1
1
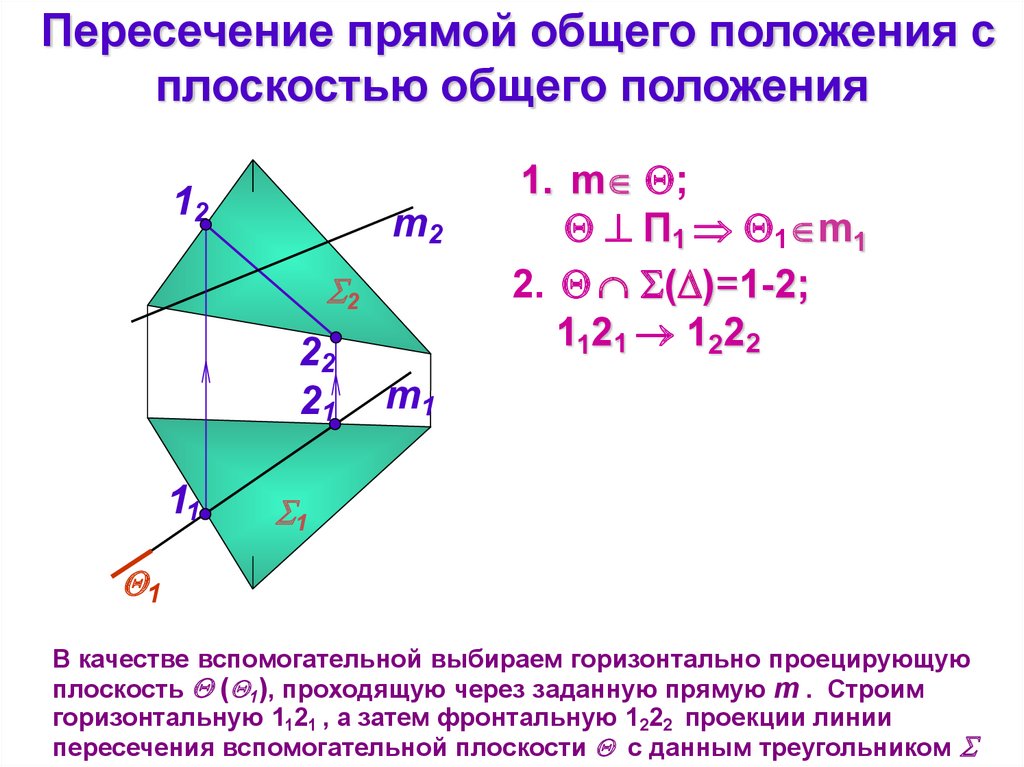
В качестве вспомогательной выбираем горизонтально проецирующую
плоскость ( 1), проходящую через заданную прямую m . Строим
горизонтальную 1121 , а затем фронтальную 1222 проекции линии
пересечения вспомогательной плоскости с данным треугольником

34.

1 ПО. Пересечение прямой общего
положения с плоскостью общего положения
12
m2
K2
22
21
11
m1
1. m ;
П1 1 m1
2. ( )=1-2;
1121 1222
3. 1-2 m = K; K2 K1
K1
1
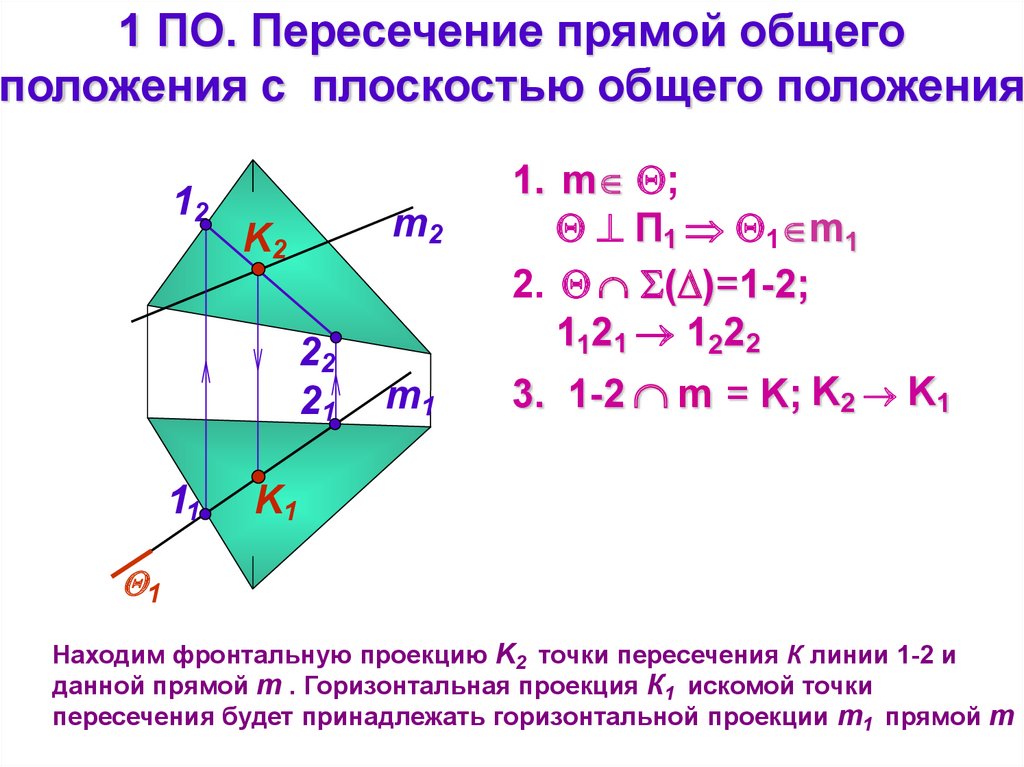
Находим фронтальную проекцию K2 точки пересечения К линии 1-2 и
данной прямой m . Горизонтальная проекция К1 искомой точки
пересечения будет принадлежать горизонтальной проекции m1 прямой m

35.

1 ПО. Пересечение прямой общего
положения с плоскостью общего положения
12
4
5
( )2
3
2
m2
22
31 (2211)
m1
K2
2
5
1
4 11
K1
1. m ;
П1 1 m1
2. ( )=1-2;
1121 1222
3. 1-2 m = K; K2 K1
4. Видимость m
(по конкурирующим точкам)
1
1
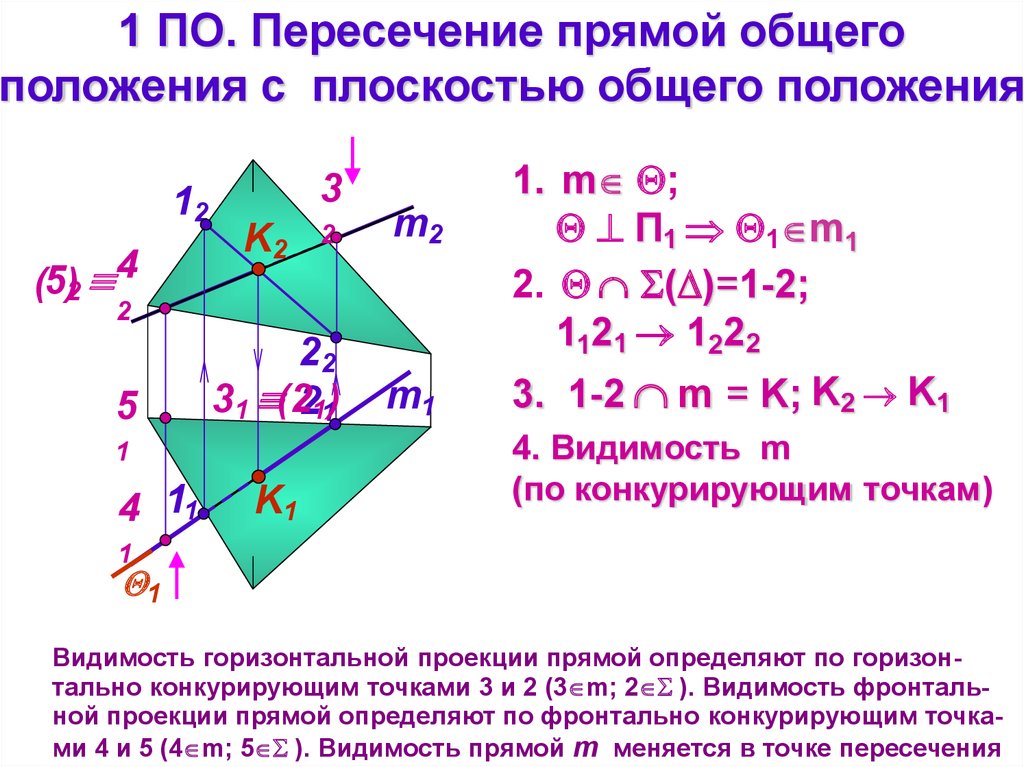
Видимость горизонтальной проекции прямой определяют по горизонтально конкурирующим точками 3 и 2 (3 m; 2 ). Видимость фронтальной проекции прямой определяют по фронтально конкурирующим точками 4 и 5 (4 m; 5 ). Видимость прямой m меняется в точке пересечения