24.84M

Категория:

Механика

Похожие презентации:

Основы теории оболочек. Общие сведения о тонких пластинах, продолжение

Изгиб пластин

Строительная механика пластин. Изгиб пластин

Механика материалов. Лекция 2. Основы теории напряженного и деформированного состояний

Основы теории напряженного состояния. Лекция 9

Уравнения строительной механики. Вариационные принципы строительной механики

Пологие оболочки. Полубезмоментная теория цилиндрических оболочек

Теория напряжений и дефомаций

Основы теории напряженного и деформированного состояний (продолжение)

Устойчивость пластин

Основы теории оболочек. Общие сведения о тонких пластинах

1.

Строительная механика
ракет-носителей
Контрольный опрос
по лекции 1.7
Основные соотношения теории упругости
для брусьев

2.

1. Определить силовые факторы
по соотношениям эквивалентности
y
Qy
Nx x
τxy
σx
z
Mz
dF
N x σ x dF
Q y τ xy dF
M z σ x zdF
F
F
F

3.

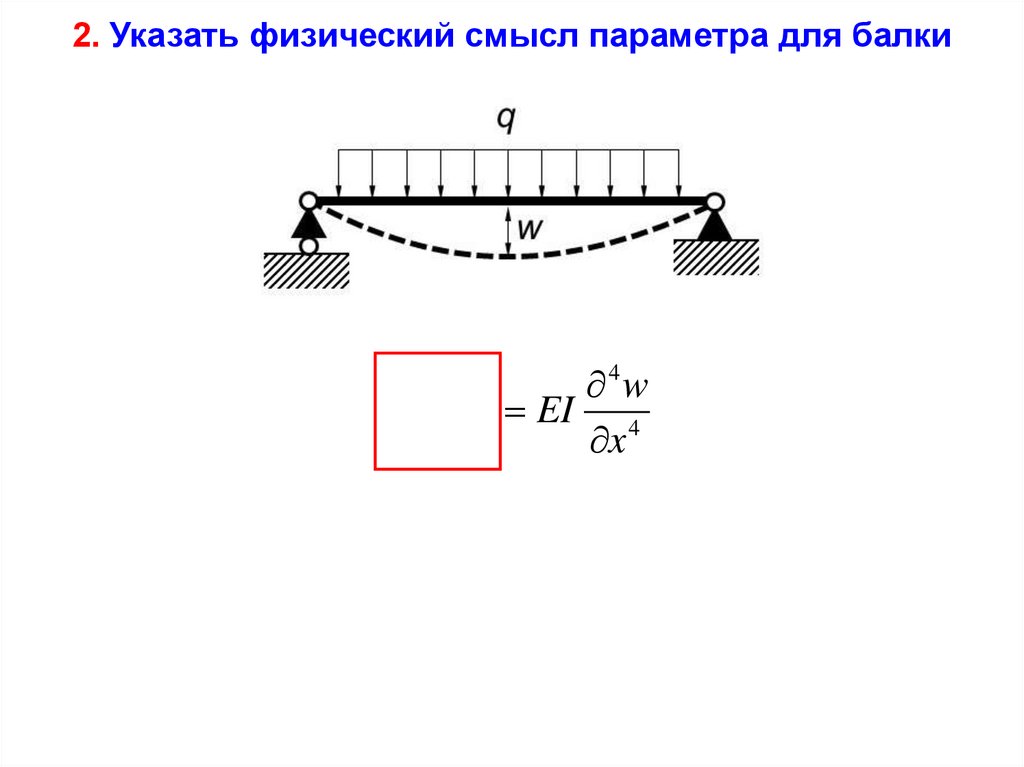
2. Указать физический смысл параметра для балки
Q
4w
q
EI 4
x
x

4.

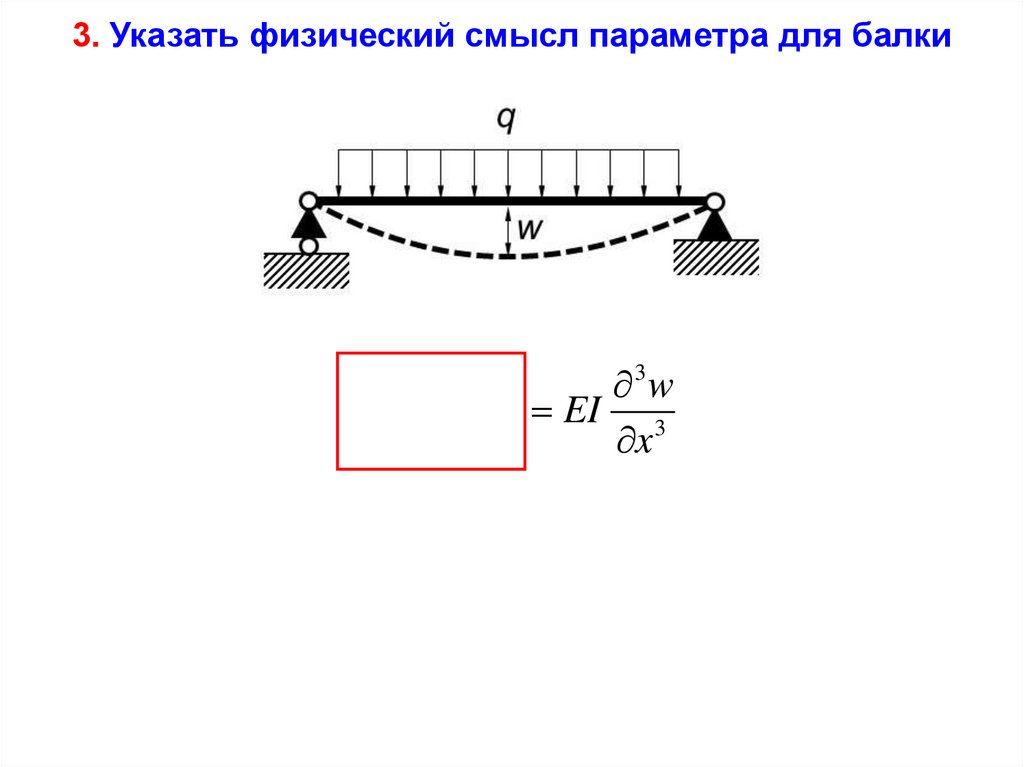
3. Указать физический смысл параметра для балки
М изг
3w
Q
EI 3
x
x

5.

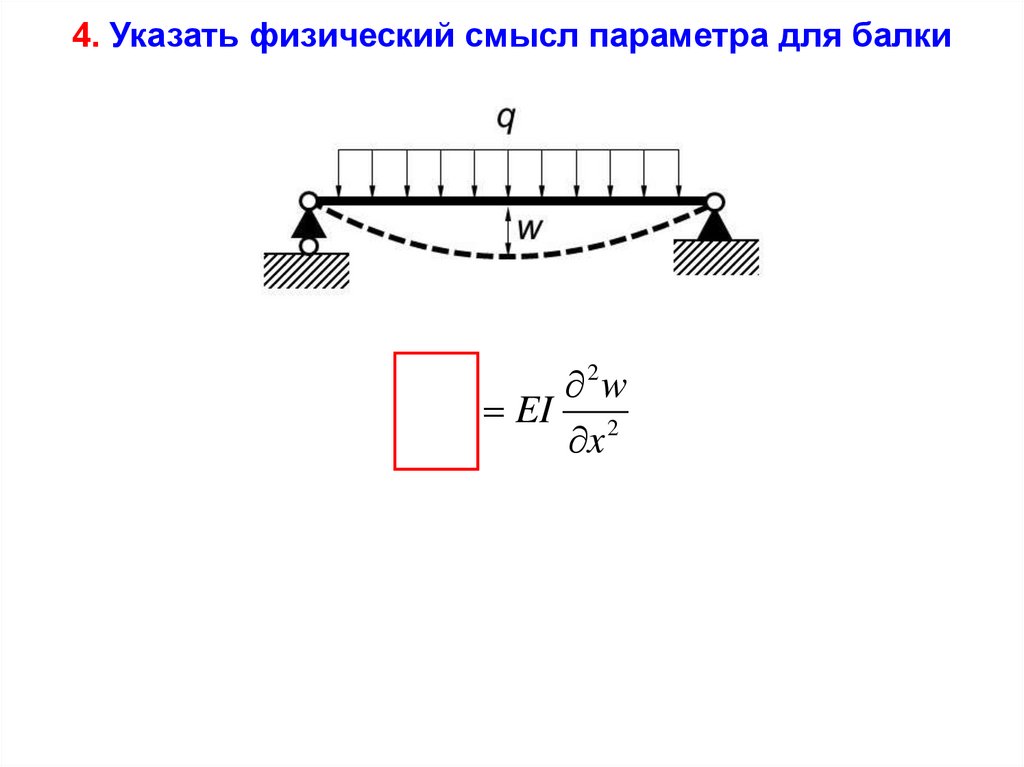
4. Указать физический смысл параметра для балки
М изг
2w
EI 2
x

6.

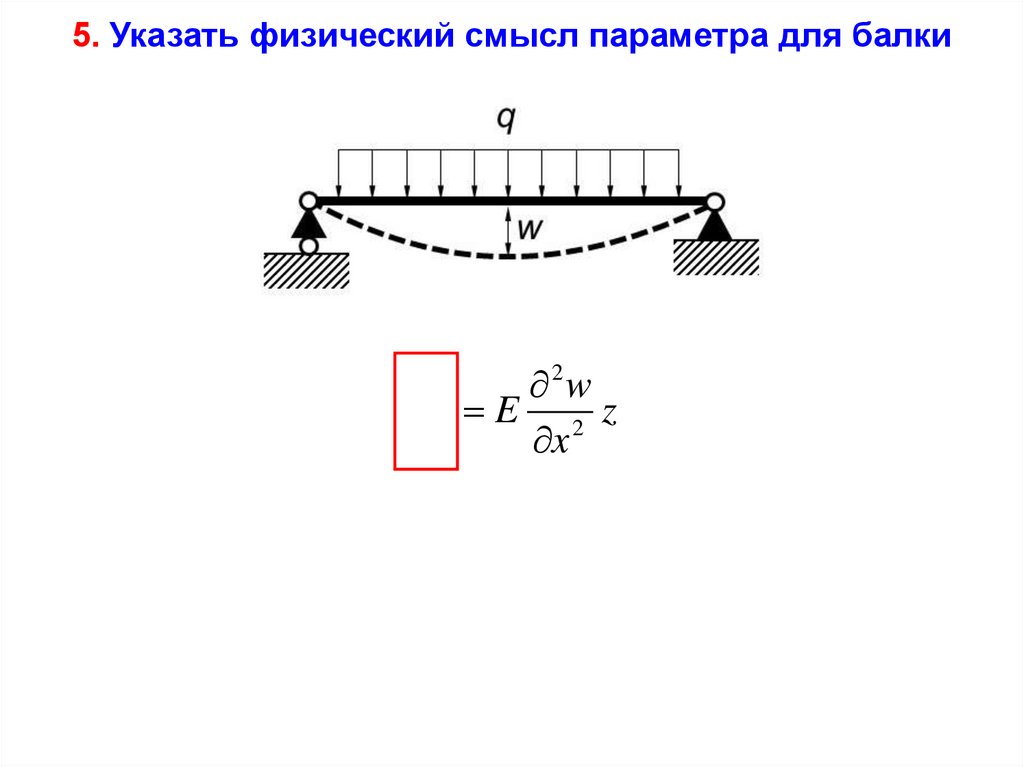
5. Указать физический смысл параметра для балки
2w
х E 2 z
x

7.

6. Указать физический смысл параметров балки
u0
z
θ
w
y
x
dx
2w
z х
2
x
2w
2
x
w
x
x

8.

Строительная механика
ракет-носителей
Ответы на вопросы
по лекции 1.7

9.

1. Определить силовые факторы
по соотношениям эквивалентности
y
Qy
Nx x
τxy
σx
z
Mz
dF
N x σ x dF
Q y τ xy dF
M z σ x zdF
F
F
F

10.

2. Указать физический смысл параметра для балки
Q
4w
q
EI 4
x
x
Распределенная поперечная нагрузка

11.

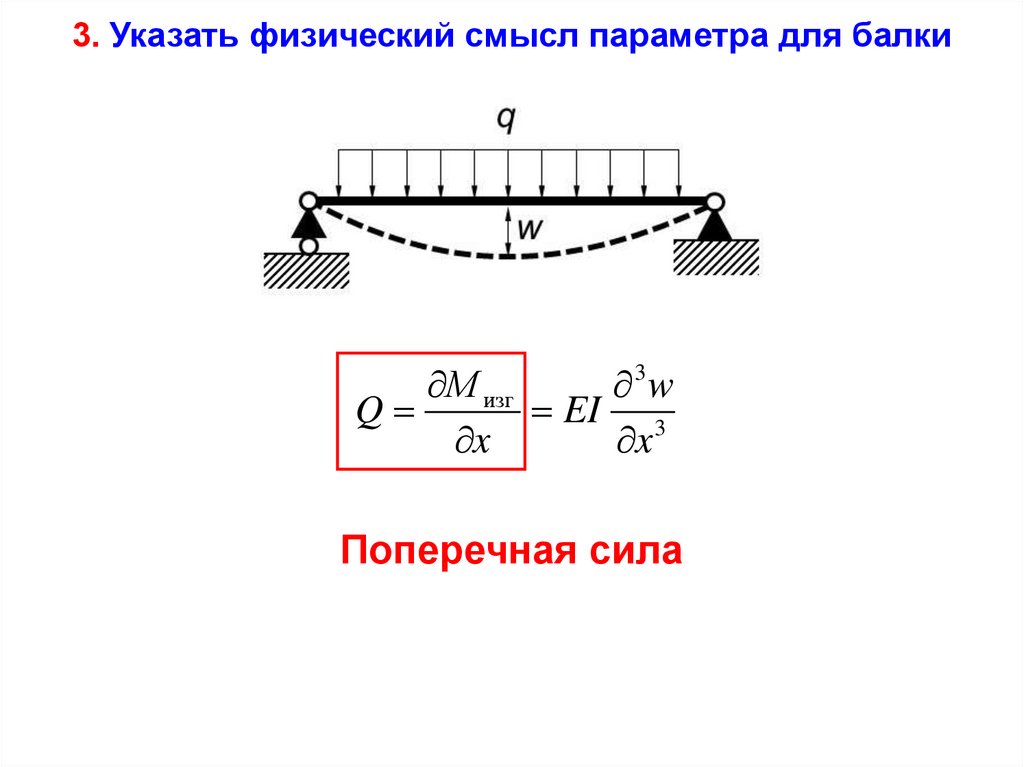
3. Указать физический смысл параметра для балки
М изг
3w
Q
EI 3
x
x
Поперечная сила

12.

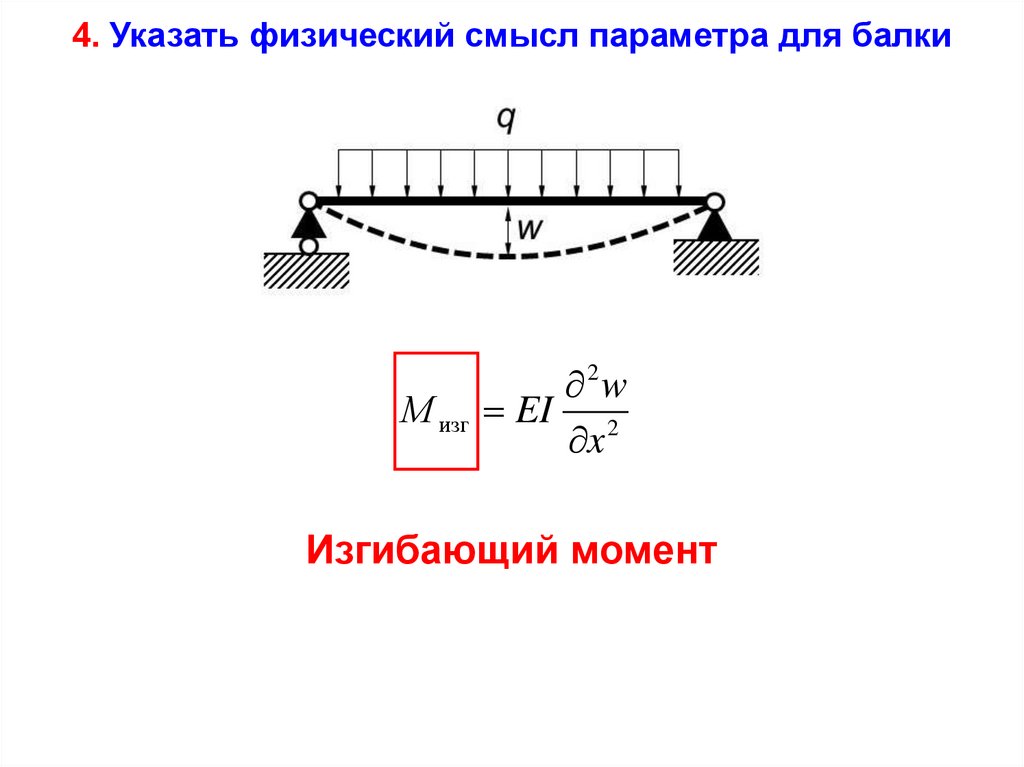
4. Указать физический смысл параметра для балки
М изг
2w
EI 2
x
Изгибающий момент

13.

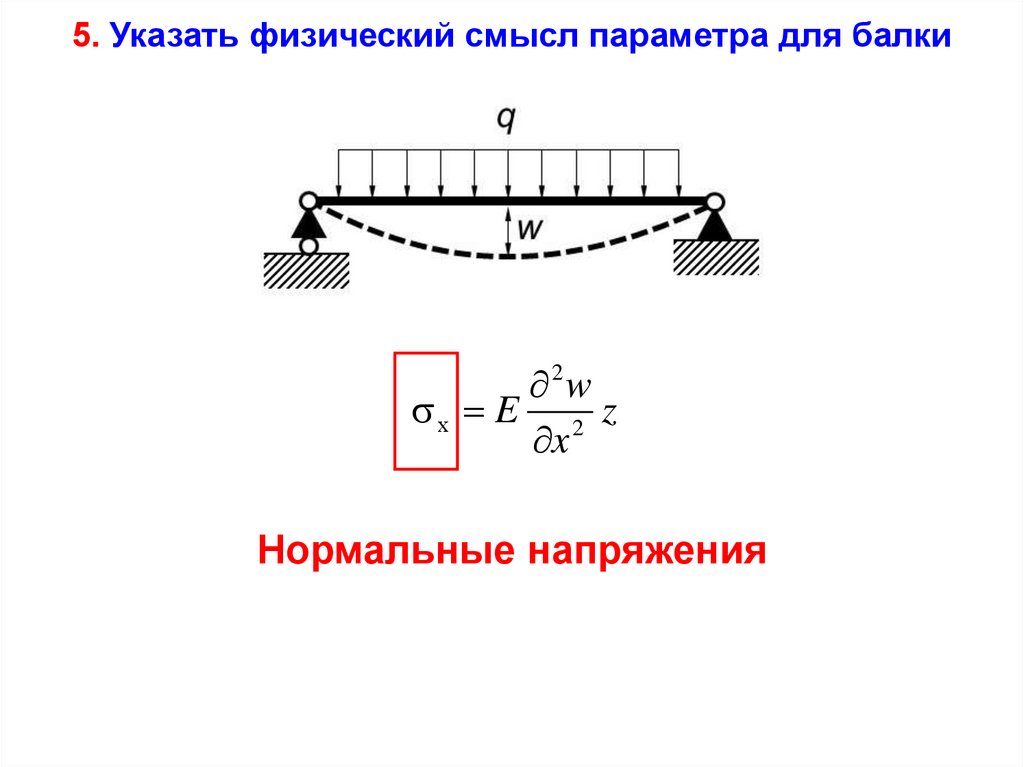
5. Указать физический смысл параметра для балки
2w
х E 2 z
x
Нормальные напряжения

14.

6. Указать физический смысл параметров балки
u0
z
θ
w
y
x
dx
2w
z х
2
x
2w
2
x
w
x
x

15.

Критерии оценки:
Оценка
«отлично» –
«хорошо» –
«удовлетворительно» –
«неудовлетворительно» –
Количество ошибок
0
1
2
3 и более

16.

Строительная механика
ракет-носителей
Тема 2
Основы теории оболочек
Лекция № 9 /2.1/
Старший преподаватель 13 кафедры
Карчин Александр Юрьевич

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.1
Общие сведения
о тонких пластинах
Вопрос 1 Классификация пластин. Гипотезы Кирхгофа
Вопрос 2 Геометрические уравнения для пластин
Вопрос 3 Физические уравнениям для пластин

18.

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.1
Общие сведения
о тонких пластинах
Карчин А.Ю., Болдырев К.Б.
Теоретические основы строительной
механики ракет-носителей
СПб.: ВКА имени А.Ф. Можайского, 2015
с. 63-68

19.

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.1
Общие сведения
о тонких пластинах
Вопрос 1 Классификация пластин. Гипотезы Кирхгофа

20.

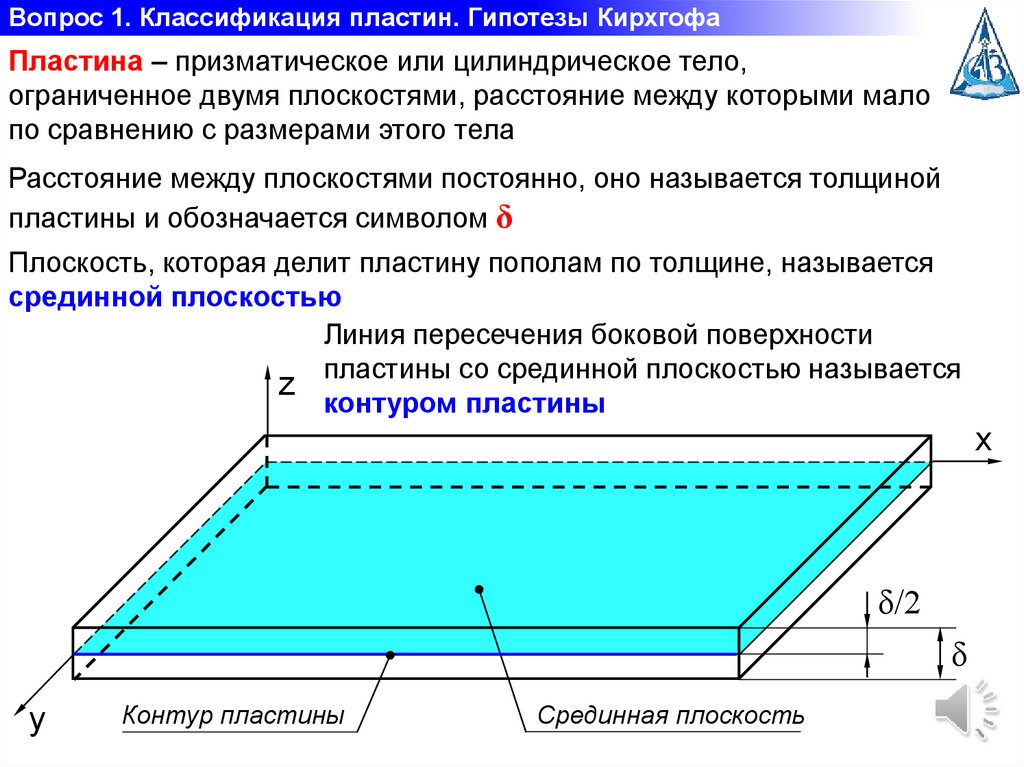
Вопрос 1. Классификация пластин. Гипотезы Кирхгофа
Пластина – призматическое или цилиндрическое тело,
ограниченное двумя плоскостями, расстояние между которыми мало
по сравнению с размерами этого тела
Расстояние между плоскостями постоянно, оно называется толщиной
пластины и обозначается символом δ
Плоскость, которая делит пластину пополам по толщине, называется
срединной плоскостью
Линия пересечения боковой поверхности
z пластины со срединной плоскостью называется
контуром пластины
x
δ/2
δ
y
Контур пластины
Срединная плоскость

21.

Вопрос 1. Классификация пластин. Гипотезы Кирхгофа
В зависимости от толщины δ пластины к ее наименьшему
габаритному размеру b, пластины принято классифицировать по группам:
Плиты
1
b 5
Пластины
1 1
40 b 5
Мембраны
1
b 40
Для расчёта тонких пластин используется приближенная теория –
техническая теория изгиба пластин, основанная на гипотезах Кирхгофа

22.

Вопрос 1. Классификация пластин. Гипотезы Кирхгофа
В основе технической теории изгиба пластин лежат гипотезы
Кирхгофа
Густав Роберт Кирхгоф (1824 - 1887) – немецкий физик
и математик
1. Гипотеза прямых нормалей: любой прямолинейный элемент
пластины, нормальный к срединной плоскости до деформирования,
остается прямолинейным и нормальным к этой плоскости после
деформирования, при этом его длина не изменяется
Согласно этой гипотезе прямые углы между прямолинейным элементом
и осями х и у остаются прямыми → сдвиги в указанных плоскостях
отсутствуют:
yz 0; xz 0

23.

Вопрос 1. Классификация пластин. Гипотезы Кирхгофа
В основе технической теории изгиба пластин лежат гипотезы
Кирхгофа
Густав Роберт Кирхгоф (1824–1887) – немецкий
физик и математик
1. Гипотеза прямых нормалей: любой прямолинейный элемент
пластины, нормальный к срединной плоскости до деформирования,
остается прямолинейным и нормальным к этой плоскости после
деформирования, при этом его длина не изменяется
Эта гипотеза также характеризует сохранение длины прямолинейного
элемента. Она предполагает, что линейная деформация в направлении
оси z (по толщине пластины) отсутствует:
z 0

24.

Вопрос 1. Классификация пластин. Гипотезы Кирхгофа
2. Гипотеза о недеформируемости срединной плоскости:
согласно этой гипотезе, срединная плоскость является нейтральной,
и в ней отсутствуют деформации растяжения, сжатия и сдвига
После деформирования плоскость не меняет площади своей поверхности.
Перемещения точек этой плоскости отсутствуют
z 0
3. Гипотеза о ненадавливаемости слоев пластины, параллельных
срединной плоскости (статическая гипотеза):
Согласно этой гипотезе, нормальные напряжения σz, которые
перпендикулярны срединной плоскости, малы по сравнению с другими
напряжениями σx и σy, действующими в плоскости пластины, и ими можно
пренебречь
z 0
В связи с этим, каждый бесконечно тонкий слой пластины, параллельный
срединной плоскости, можно рассматривать в условиях плоского
напряженного состояния

25.

26.

Вопрос 2. Геометрические уравнения для пластин
Учитывая 1-ю гипотезу и геометрические соотношения,
прогибы пластины w не зависят от координаты z,
а изменяются только при смене двух координат → w = f(x, y)
w
z
0
z
→ все точки пластины, которые лежат на одной вертикали, получают
одинаковые перемещение w
Для отыскания вертикальных перемещений всех точек пластины
достаточно определить только прогибы её срединной плоскости
На основании данных об отсутствии сдвигов при изгибе пластины,
из геометрических соотношений, можно утверждать:
v w
yz
0
z y
Эти соотношения позволяют
найти производные
составляющих перемещений u и v:
u w
xz
0
z x
v
w
z
y
u
w
z
x

27.

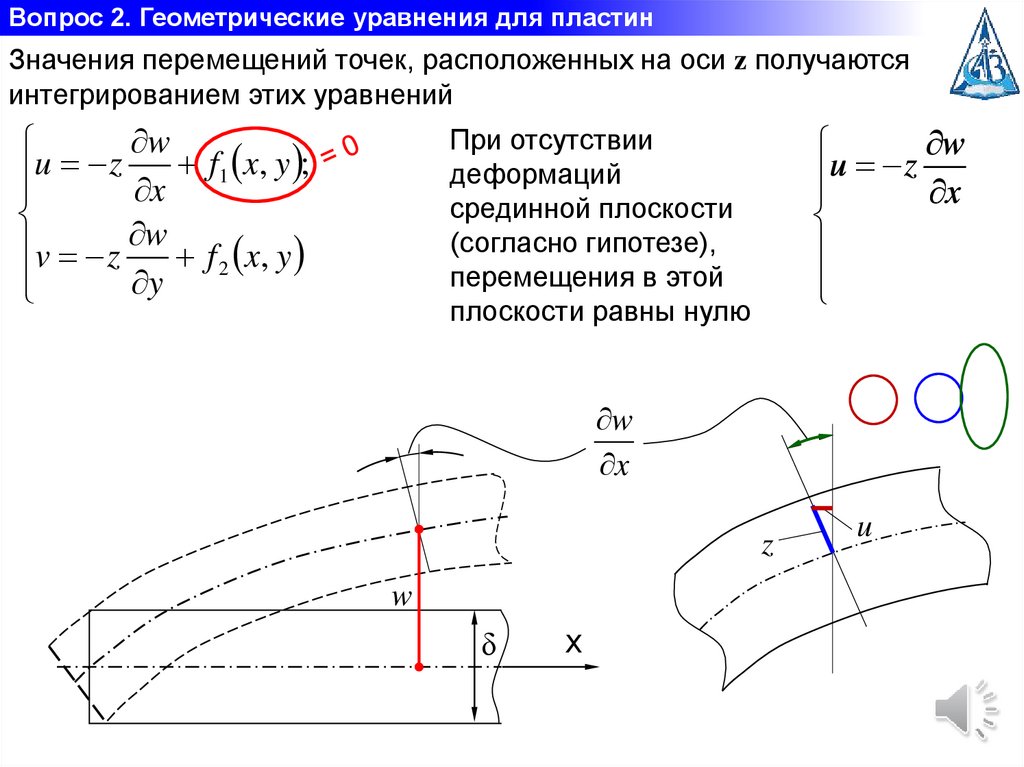
Вопрос 2. Геометрические уравнения для пластин
Значения перемещений точек, расположенных на оси z получаются
интегрированием этих уравнений
w
u
z
f1 x, y ;
x
v z w f 2 x, y
y
При отсутствии
деформаций
срединной плоскости
(согласно гипотезе),
перемещения в этой
плоскости равны нулю
w
u z x
v z w
y

28.

Вопрос 2. Геометрические уравнения для пластин
Значения перемещений точек, расположенных на оси z получаются
интегрированием этих уравнений
w
u
z
f1 x, y ;
x
v z w f 2 x, y
y
w
u z x
v z w
y
При отсутствии
деформаций
срединной плоскости
(согласно гипотезе),
перемещения в этой
плоскости равны нулю
w
x
z
w
δ
x
u

29.

30.

Вопрос 2. Геометрические уравнения для пластин
Для отличающихся от нуля составляющих деформации пластины,
необходимо воспользоваться геометрическими уравнениями
и подставить в них значения составляющих перемещения
u
2w
z 2
x
x
x
v
2w
z 2
y
y
y
u v
2w
2 z
xy
y x
x y
w
u z x
v z w
y
В этом выражении составляющие деформации, так же как
и составляющие перемещения в соотношениях, выражены
через функцию прогибов срединной плоскости пластины → w = f(x, y)

31.

32.

Вопрос 3. Физические уравнения для пластин
Согласно обобщенному закону Гука:
Физические соотношения для пластины записываются с учетом
основных гипотез Кирхгофа σz = 0; εz= 0; γyz = γzx = 0;
E
xy G xy ;
x 1 2 x ( y z ) ;
E
(
)
;
y
y
x
z
2
yz G yz ;
1
E
z ( x y )
z
2
zx G zx
1
E
x 1 2 x y ;
E
y x ;
y
2
1
E
xy
xy
2 1

33.

Вопрос 3. Физические уравнения для пластин
С учетом геометрических соотношений для пластины
Е д2 w
д2 w
z 2 2 ;
x
2
1 дx
дy
Е д2 w
д2 w
z 2 2 ;
y
2
1 дy
дx
Е
2w
xy
z
.
(1 ) x y
E
x 1 2 x y ;
E
y x ;
y
2
1
E
xy
xy
2 1

34.

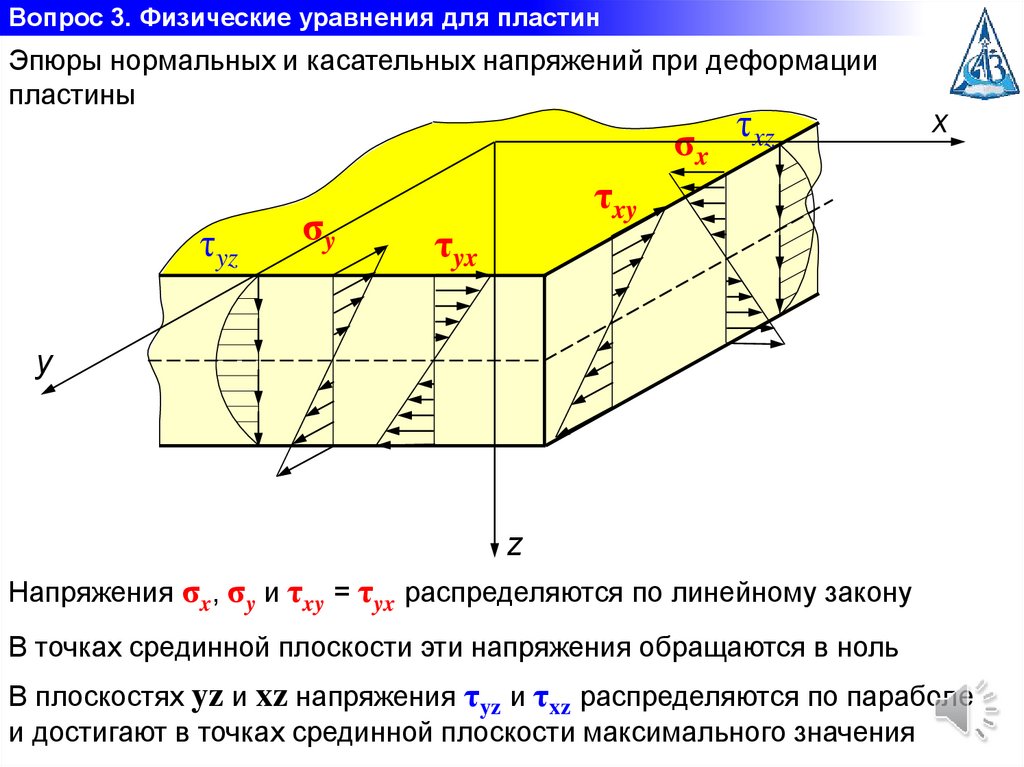
Вопрос 3. Физические уравнения для пластин
Эпюры нормальных и касательных напряжений при деформации
пластины
σx
τyz
σy
τxz
x
τxy
τyx
y
z
Напряжения σx, σy и τxy = τyx распределяются по линейному закону
В точках срединной плоскости эти напряжения обращаются в ноль
В плоскостях yz и xz напряжения τyz и τxz распределяются по параболе
и достигают в точках срединной плоскости максимального значения

35.

Вопрос 3. Физические уравнения для пластин
Выражения для касательных напряжений τyz и τxz определяются
интегрированием уравнений равновесия Навье.
х yх zх
0;
y
z
х
xy y zy
0;
y
z
x
yz z
xz
0.
x
y
z
zх
х yх
Еz
z
х
y
1 2
Еz
x
1 2
2w
2w
2 2
y
x
Еz 2 w
xy
1 x y
3w
3w
Ez
3w
3
z
2
2
x
xдд
1
x
y
Еz 2
zх
Еz 2 w 2 w
2 2
w
2
2
z
1 x x
y 1 x

36.

Вопрос 3. Физические уравнения для пластин
Для определения τyz и τxz используют оператор Лапласа,
который применяется в уравнениях физики сплошных сред
2
2
2
2
2 2 2
y
z
x
Пьер-Симо́н, маркиз де Лапла́с (1749-1827) –
французский математик, механик, физик и астроном
xz
Еz д 2
w
2
z 1 дx
Интегрируя по Z, →
Ez 2 2
zx xz
w f 3 x, y
2
2 1 x
Для определения произвольной функции f3(x,y) рассматриваются
граничные условия, когда касательные напряжения отсутствуют на
поверхностях пластины →
zx xz 0
z
2

37.

Вопрос 3. Физические уравнения для пластин
E 2 2
zx xz
w f 3 x, y 0
2
8 1 x
E 2 2
f 3 x, y
w
2
8 1 x
Ez 2 2
E 2 2
zx xz
w
w
2
2
2 1 x
8 1 x
2
Ez E
22 2 2
Касательные напряжения
zxzx xzxz
w
f
x
,
y
z
w
3
x
2 12 1
2 2 x 4
в плоскости xz
E
zy yz
2 1 2
2
z 2 2 w
4
y
Аналогично,
касательные напряжения
в плоскости yz

38.

Вопрос 3. Физические уравнения для пластин
Система уравнений, определяющих напряжения при деформации
пластины, с учетом геометрических уравнений:
Полученные формулы выражают все
Е 2w
2w
x
z 2 2 ; напряжения через одну функцию
2
1 x
y
двух переменных f = w(x,y) →
2
2
y Е z w w ;
прогиб срединной плоскости
1 2 y 2
x 2
Е
2w
z
;
xy
1 y x
2
E
2
2
zx
z
w;
2
2(1 ) 4
x
2
E
2
2
zy
z
w
2
2(1 ) 4
y

39.

40.

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.1
Общие сведения
о тонких пластинах
Вопросы для самоконтроля:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Что называется пластиной?
Что называется срединной плоскостью пластины?
Как классифицируются пластины?
Как сформулировать гипотезы Кирхгофа для пластин?
Записать систему геометрических соотношений для платин?
Как зависят перемещения в пластине w от координаты z?
Как выглядит система физических соотношений для платин?
Чему равны деформации вдоль оси z?
Как распределены нормальные и касательные напряжения
по толщине пластины?

41.

42.

English Русский Правила