Похожие презентации:
Теория напряжений и дефомаций
1. Лекция 2 Теория напряжений и деформаций
Доцент кафедрысамолетостроения
к.т.н Мухин Д.В.
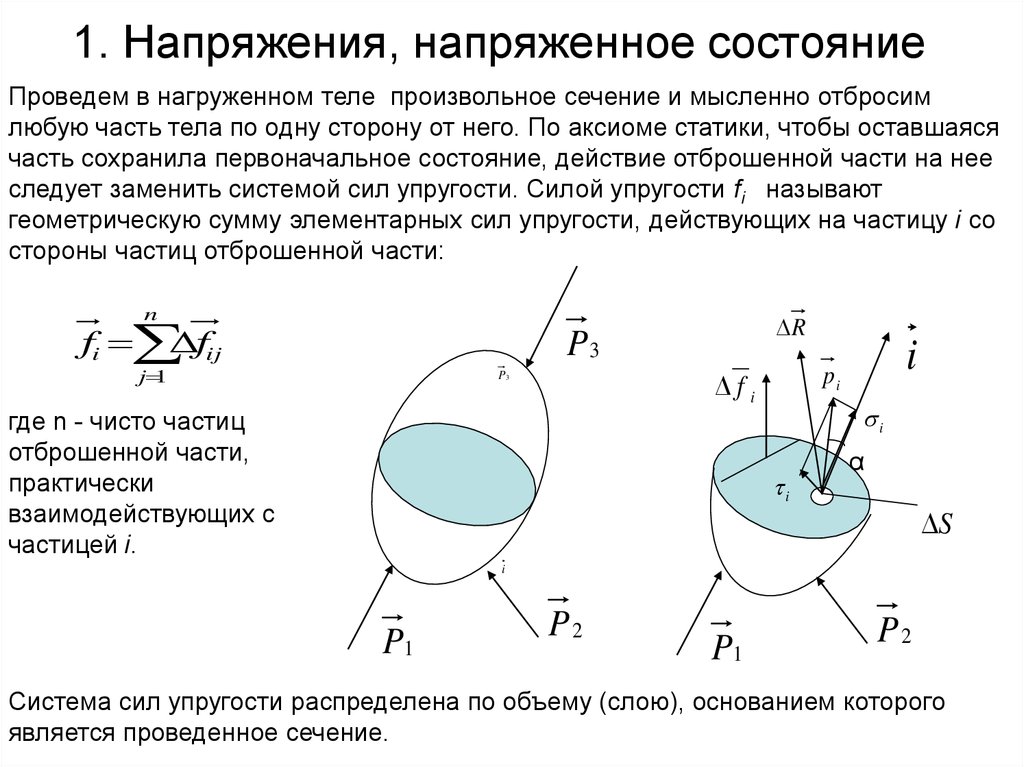
2. 1. Напряжения, напряженное состояние
Проведем в нагруженном теле произвольное сечение и мысленно отбросимлюбую часть тела по одну сторону от него. По аксиоме статики, чтобы оставшаяся
часть сохранила первоначальное состояние, действие отброшенной части на нее
следует заменить системой сил упругости. Силой упругости fi называют
геометрическую сумму элементарных сил упругости, действующих на частицу i со
стороны частиц отброшенной части:
n
fi fij
R
P3
j 1
где n - чисто частиц
отброшенной части,
практически
взаимодействующих с
частицей i.
i
pi
fi
P3
i
i
α
S
i
P1
P2
P1
P2
Система сил упругости распределена по объему (слою), основанием которого
является проведенное сечение.
3.
Поверхностная плотность или интенсивность сил упругости в произвольнойточке О сечения, нормаль к которому i определяется напряжением pi как
предел отношения R S при S 0, где S - площадка, окружающая точку
O. R -равнодействующая сил упругости, действующих по этой площадке
R
pi lim
S
0
S
dR
pi
dS
Для удобства физическою и математического анализа напряжение разлагается
на нормальное и касательное, являющиеся соответственно составляющими p,
по нормали к сечению и по его плоскости.
i pi cos
i pi sin
Напряжение в данной точке тела зависит от величин и законов распределения
внешних факторов, от положения сечения, проходящего через эту точку, от
геометрии тела
4.
Механическое напряжение — это мера внутренних сил, возникающих вдеформируемом теле, под влиянием внешних факторов и равное отношению
внутренней силы упругости, возникающей в теле при деформации к площади
малого элемента сечения, перпендикулярного к этой силе в данной точке
рассматриваемого сечения. ∙
Различают две составляющие вектора механического напряжения:
Нормальное механическое напряжение — действует на площадку сечения по
направлению нормали к сечению (обозначается σ). [МПа]
Касательное механическое напряжение — действует на площадку сечения в
плоскости сечения по касательной (обозначается τ). [МПа]
Совокупность напряжений, действующих по различным площадкам, проведенным
через данную точку, называется напряженным состоянием в точке.
5.
Связь напряжений и внутренних силовых факторовВнутренние силовые факторы могут быть выражены через напряжения,
действующие на поперечном сечении стержня
N xdA
y
A
Qy
xydA
τxy
τxz
A
Q
xzdA
z
A
M
dA
K
A
M
xydA
z
A
M
xzdA
y
A
dA
z
z
σx
y
x
6.
Компоненты напряженного состояния исвойство парности касательных напряжений
При действии на тело внешних факторов в нем возникают силы
упругости, поверхностная плотность которых в каждой точке любого
сечения тела определяется напряжением. Это состояние тела
называется напряженным.
Свяжем с телом систему координатных
осей х0, у0, z0 и у его произвольной
точки О мысленно вырежем элемент с
гранями, параллельными
координатным плоскостям (взаимно
P3
перпендикулярными), и бесконечно
малыми ребрами dx, dy, dz.
Заменим действие отброшенных
P2
частей тела на элемент силами
упругости, которые ввиду бесконечной
малости ребер можно считать
равномерно распределенными по
гpaням. Интенсивность сил упругости
зададим напряжениями, которые на
каждой грани разложим по
P1
координатным осям .
7.
zZ
ZX
ZY
XZ
dy
dx
dz
XY
X
XY
X
YZ
XZ
y
YХ
Y
Y
ZХ
ZY
Z
YX
YZ
x
8.
Составляющие (проекции) напряжений, действующих по граням,совпадающим с координатными плоскостями, но координатным осям
(на координатные оси), называются компонентами напряженного
состояния в данной точке тела, определяющими напряженное
состояние в этой точке.
Нормальным напряжениям присваивается индекс нормали к грани, по которой
они действуют, а касательным напряжениям - два индекса: первый - нормаль к
грани, по которой они действуют, а второй - ось, которой они параллельны.
Нормальный компонент считается положительным, если он действует от грани.
Касательный компонент положителен, если, действуя по грани, внешняя
нормаль к которой совпадает по направлению с координатной осью, сам
совпадает по направлению с координатной осью, которой он параллелен, или
наоборот.
Вырезанный элемент должен находиться в равновесии, поэтому сумма моментов
всех сил, на него действующих относительно любой оси, например оси z, должна
равняться нулю.
m
dxdydz
dxdydz
0откуда
z
Аналогично
xy
yx
yz zy
xz zx
xy
yx
9.
Закон парности касательных напряжений:по взаимно перпендикулярным площадкам действуют равные
касательные напряжения, направленные или к линии их
пересечения, или от нее.
Напряженное состояние тела будет определено, если будут найдены шесть
компонентов напряженного состояния σx, σy, σz, τxy, τyz, τxz в каждой его точке.
Эти шесть составляющих образуют тензор напряжений второго ранга симметричный относительно главной диагонали, который можно изобразить
следующей матрицей:
x xy xz
yx y yz
zx zy z
10. 2. Напряжения по наклонным площадкам
Рассмотрим зависимости междукомпонентами тензора напряжений и
составляющими полного напряжения σn ,
действующего по наклонной площадке.
На слайде изображен элементарный
тетраэдр. Площади его граней,
совпадающих с координатными
плоскостями, выражаются через
площадь наклонной грани dS по теореме
о проектировании площади следующим
образом
dSx dS nx ,
dSy dS ny ,
dSz dS nz .
T
Где n
- вектор нормали к наклонной площадке
n
i
n
j
n
k
n
,
n
,
n
x
y
z
x yz
- направляющие косинусы нормали n к
n
cos
n
,
x
,
n
cos(
n
,
y
),
n
cos
n
,
z
x
y
z
площадке dS
11.
На гранях, совпадающих с координатными плоскостями, действуют следующиенапряжения:
грань
dS
, xz
x:
x, xy
грань
dS
, yz
y:
y, yx
грань
dS
, zy
z:
z, zx
На наклонной площадке действует напряжение σn с составляющими (σnx,σny,σnz).
Составим условия равновесия тетраэдра. Например, сумма проекций всех сил на
ось х:
dS
dS
dS
dS
nx
x x
yx
y
zx
z
откуда с учетом соотношений для dSx, dSy, dSz получим:
n
n
n
nx
x
x
yx
y
zx
z
Аналогично получаются еще два соотношения для σny и σnz. Окончательно
имеем:
nx xnx yxny zxnz
ny xynx yny zynz
nz xznx yzny znz
Соотношения, полученные нами, служат для установления граничных условий.
12.
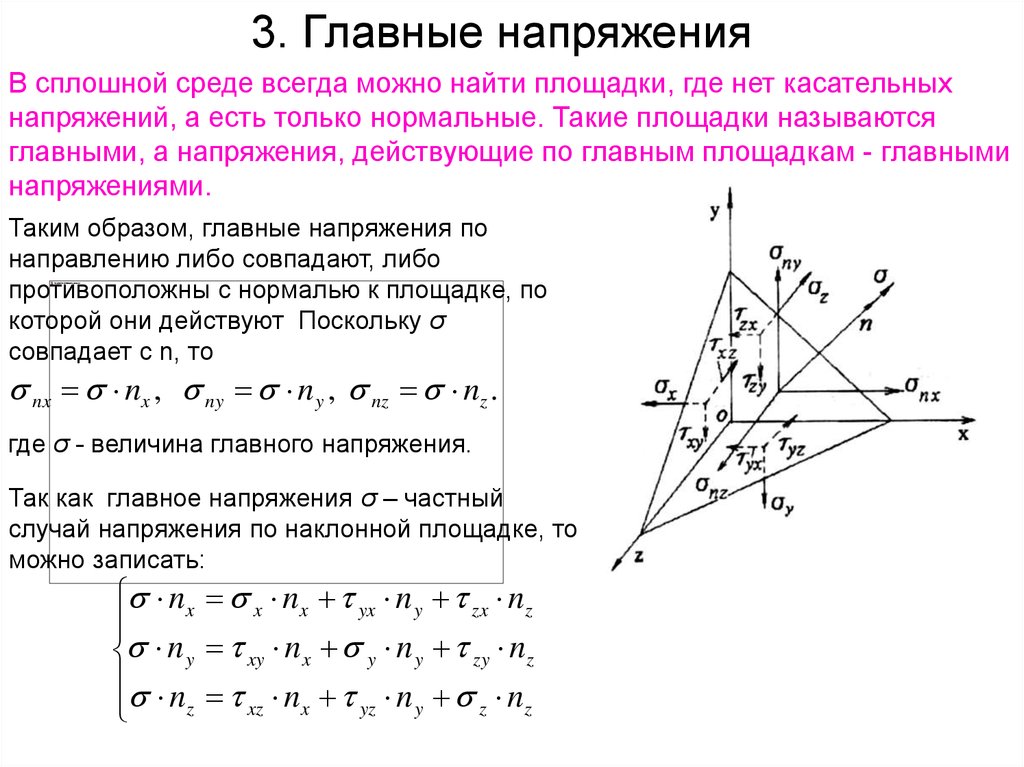
3. Главные напряженияВ сплошной среде всегда можно найти площадки, где нет касательных
напряжений, а есть только нормальные. Такие площадки называются
главными, а напряжения, действующие по главным площадкам - главными
напряжениями.
Таким образом, главные напряжения по
направлению либо совпадают, либо
противоположны с нормалью к площадке, по
которой они действуют Поскольку σ
совпадает с n, то
nx nx , ny n y , nz nz .
где σ - величина главного напряжения.
Так как главное напряжения σ – частный
случай напряжения по наклонной площадке, то
можно записать:
nx x nx yx n y zx nz
n y xy nx y n y zy nz
n n n n
z
xz
x
yz
y
z
z
13.
Алгебраически преобразуем:x nx yx n y zx nz 0;
xy nx y n y zy nz 0;
n n n 0.
yz
y
z
z
xz x
Система уравнений является однородной (свободные члены равны нулю),
поэтому ее нетривиальное решение существует только в том случае, когда ее
определитель равен нулю:
x
yx
zx
xy
y
zy 0
xz
yz
z
Раскрывая определитель, получим кубическое уравнение:
x yx zx
3 x y z 2 x y y z z x xy2 yz2 zx2 xy y zy 0
xz yz z
Три корня этого уравнения представляют собой три главных напряжения σ1, σ2, σ3.
σ1 – наибольшее (с учетом знака) из трех главных напряжений;
σ3 - наименьшее (с учетом знака ) из трех главных напряжений.
14.
Зная эти величины, с помощью уравнения системы уравнений и соотношенияможно найти направляющие косинусы главных площадок
Из свойств кубического уравнения (теорема Виета)
Инварианты тензора напряжения (не зависят от координатных осей)
15. 4. Круговая диаграмма напряженного состояния
Рассмотрим условия равновесия треугольнойпризмы. Эта призма образована путем
сечения элементарного параллелепипеда
наклонной площадкой, которая, независимо
от угла наклона α, остается параллельной
одной из главных осей. В данном случае
такой осью является главная ось y.
Проецируя все силы, действующие на
отсеченную призму, на оси, параллельные
векторам σ и τ, получим
или
16.
Эти выражения можно переписать в видеТаким образом определяют напряжения в семействе площадок, параллельных
одной из главных осей. Выражениям можно дать простое геометрическое
толкование. Перенесем полусумму главных напряжений в левую часть первого
уравнения. Далее, возводя в квадрат левые и правые части уравнений, исключаем
угол α. Получим
В системе координат σ, т это есть
уравнение окружности, Радиус
окружности равен полуразности
главных напряжений.
Полученный круг называется
кругом Мора, или круговой
диаграммой напряженного
состояния.
17.
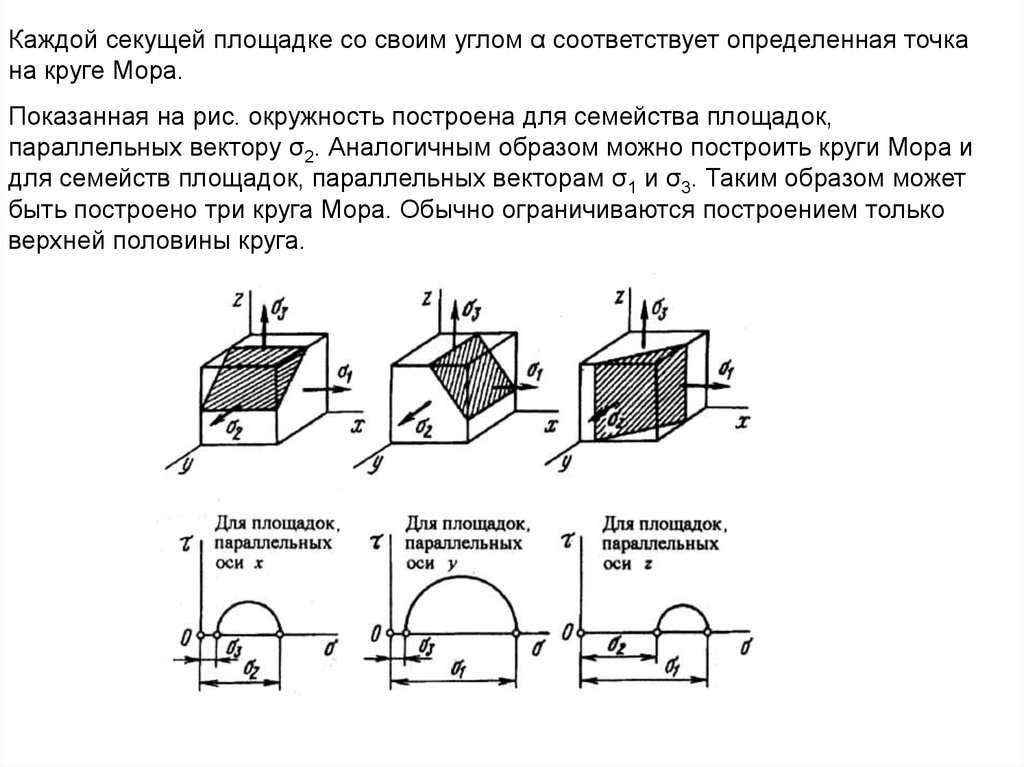
Каждой секущей площадке со своим углом α соответствует определенная точкана круге Мора.
Показанная на рис. окружность построена для семейства площадок,
параллельных вектору σ2. Аналогичным образом можно построить круги Мора и
для семейств площадок, параллельных векторам σ1 и σ3. Таким образом может
быть построено три круга Мора. Обычно ограничиваются построением только
верхней половины круга.
18.
Каждой точке любой окружности соответствует определенная секущая площадка всоответствующем семействе. Понятно, однако, что точки, расположенные на трех
кругах, не исчерпывают всего множества секущих площадок. Площадки, не
параллельные ни одной из главных осей, не вписываются в рассматриваемую
схему.
Можно показать, что секущим площадкам соответствуют на плоскости σ, τ точки,
лежащие внутри заштрихованного криволинейного треугольника BCD,
образованного тремя совмещенными кругами Мора.
Имеются также и методы определения
напряжений в соответствующих
площадках.
Поскольку ни одна из точек не выходит
за пределы заштрихованного
криволинейного треугольника,
наибольшее касательное напряжение
равно радиусу наибольшего круга
Это напряжение возникает в площадке, равнонаклоненной к главным
площадкам, на которых действуют максимальное и минимальное из главных
напряжений
19.
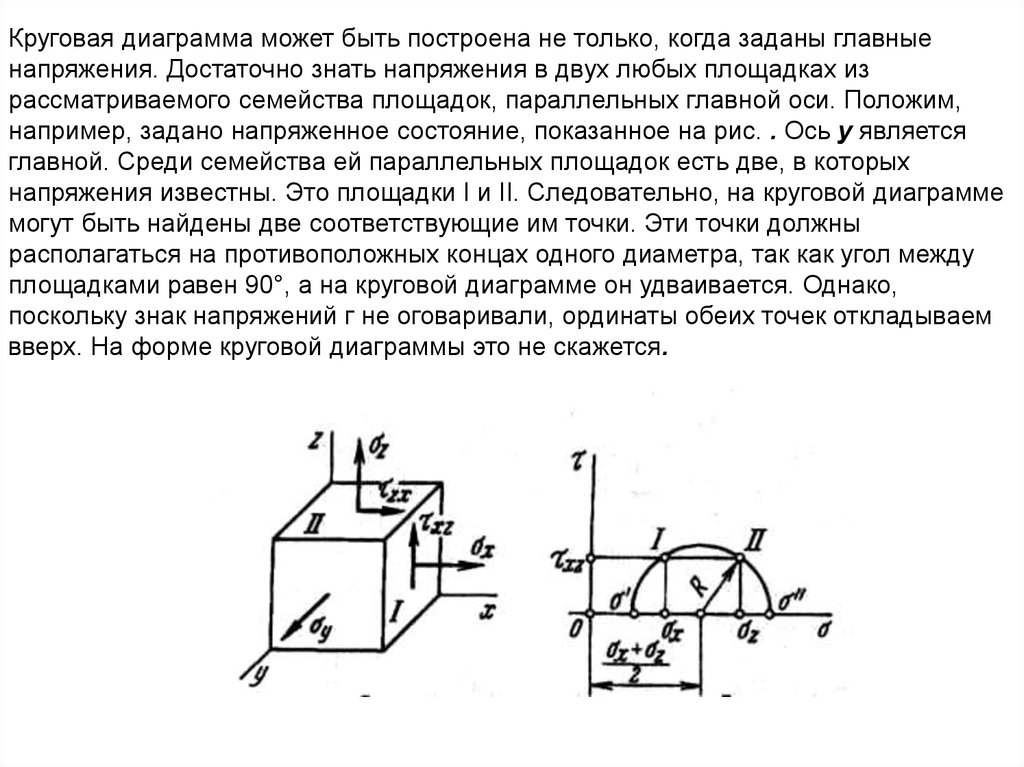
Круговая диаграмма может быть построена не только, когда заданы главныенапряжения. Достаточно знать напряжения в двух любых площадках из
рассматриваемого семейства площадок, параллельных главной оси. Положим,
например, задано напряженное состояние, показанное на рис. . Ось у является
главной. Среди семейства ей параллельных площадок есть две, в которых
напряжения известны. Это площадки I и II. Следовательно, на круговой диаграмме
могут быть найдены две соответствующие им точки. Эти точки должны
располагаться на противоположных концах одного диаметра, так как угол между
площадками равен 90°, а на круговой диаграмме он удваивается. Однако,
поскольку знак напряжений г не оговаривали, ординаты обеих точек откладываем
вверх. На форме круговой диаграммы это не скажется.
20.
Из круговой диаграммы легко определить главные напряжения:где R - радиус круга.
Таким образом
После того как напряжения σ' и σ'' найдены, их сопоставляют с σy и все главные
напряжения переименовывают на σ1, σ2 и σ3 в порядке убывания.
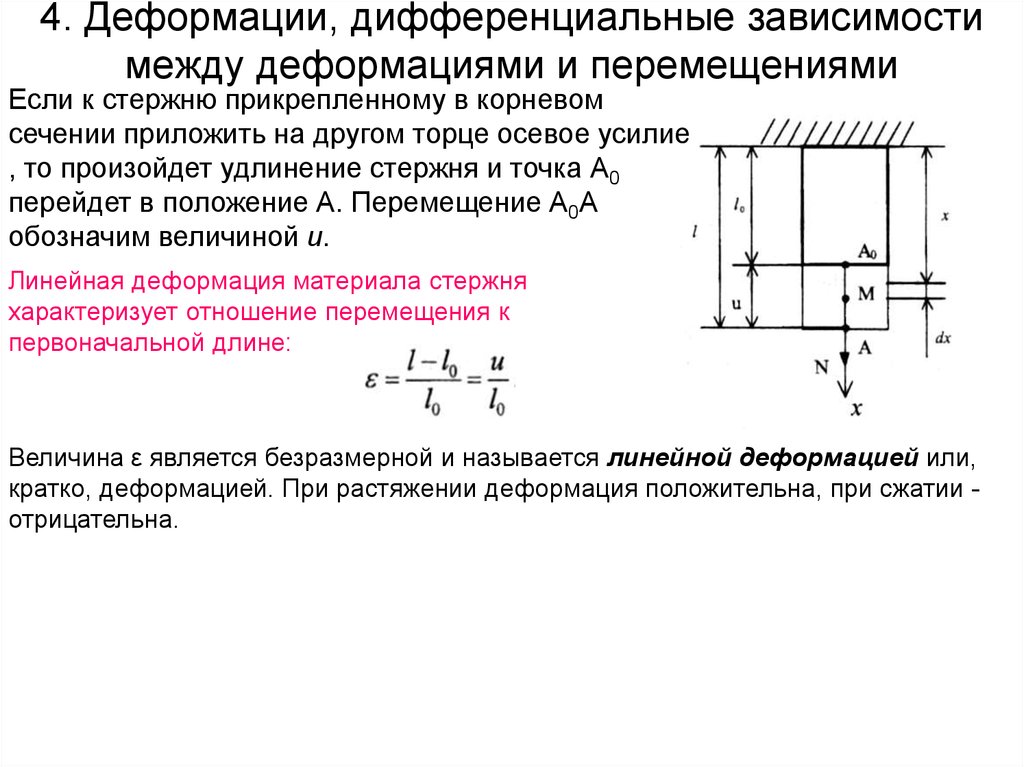
21. 4. Деформации, дифференциальные зависимости между деформациями и перемещениями
Если к стержню прикрепленному в корневомсечении приложить на другом торце осевое усилие
, то произойдет удлинение стержня и точка А0
перейдет в положение А. Перемещение А0А
обозначим величиной u.
Линейная деформация материала стержня
характеризует отношение перемещения к
первоначальной длине:
Величина ε является безразмерной и называется линейной деформацией или,
кратко, деформацией. При растяжении деформация положительна, при сжатии отрицательна.
22.
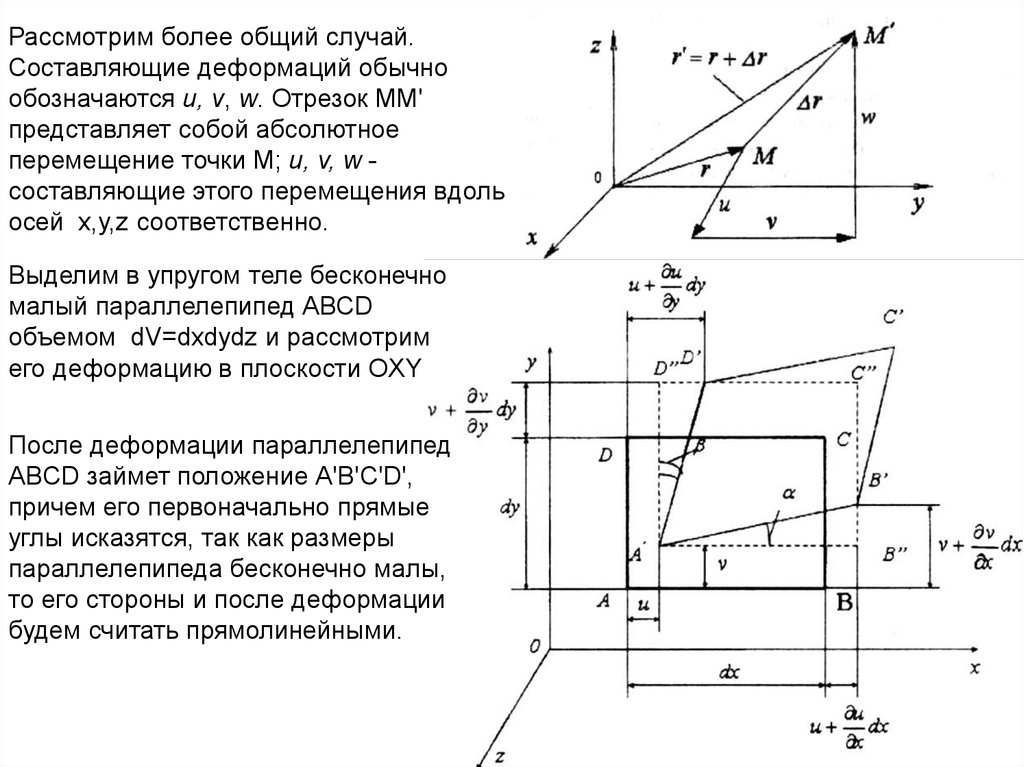
Рассмотрим более общий случай.Составляющие деформаций обычно
обозначаются u, v, w. Отрезок ММ'
представляет собой абсолютное
перемещение точки М; u, v, w составляющие этого перемещения вдоль
осей x,y,z соответственно.
Выделим в упругом теле бесконечно
малый параллелепипед АВСD
объемом dV=dxdydz и рассмотрим
его деформацию в плоскости OXY
После деформации параллелепипед
ABCD займет положение А'В'C'D',
причем его первоначально прямые
углы исказятся, так как размеры
параллелепипеда бесконечно малы,
то его стороны и после деформации
будем считать прямолинейными.
23.
Следовательно, можно написать:u x, y, z
dx
x
v x, y, z
v( x dx, y, z ) v( x, y, z )
dx
x
u ( x dx, y, z ) u ( x, y, z )
Определим относительную деформацию отрезков, параллельных координатным
осям. Рассмотрим их разность до и после деформации,
u x, y, z
dx
x
v x, y, z
v( x dx, y, z ) v( x, y, z )
dx
x
u ( x dx, y, z ) u ( x, y, z )
Поделим эту разность на длину отрезка до деформации, получим значения
линейных деформаций, например для линейной деформации вдоль оси х - εх,
будет
u x, y, z
dx
u
x
x
;
dx
x
Аналогично
y
v
w
; z
.
y
z
24.
Рассмотрим угловую деформацию.Деформация угла DAB будет равна α+β.
Поскольку деформации малы то
sin tg ;
sin tg .
По определению тангенса
v
dx
B B
v
x
tg
;
A B
dx
x
u
dy
DD
u
y
tg
.
A D
dy
y
Следовательно полная угловая
деформация равна:
xy
u v
.
y x
По закону парности:
xy yx
Аналогично
u w
z x
w v
.
y z
xz zx
zy yz
25.
Окончательно получаем:(геометрические
соотношения Коши)
u
u v
, xy
,
x
y x
v
v w
y , yz
,
y
z y
w
w u
z
, zx
,
z
x z
x
Правило знаков:
Удлинение - положительная деформация.
Уменьшение первоначально прямого угла - положительный сдвиг.
Деформации, как и напряжения, образуют тензор второго ранга – тензор
деформаций, который изображается матрицей:
Любой тензор, а значит, и тензор деформаций, имеет главные оси и три
инварианта.
26.
5. Условия совместности деформаций СенВенанаШесть деформаций εx, εy, εz, γxy, γyz, γxz выражаются через три перемещения u, v, w.
Следовательно, деформации не могут быть произвольными функциями координат
и между ними должна быть связь. Уравнения связи между деформациями делятся
на две группы и называются условиями сплошности Сен-Венана.
ПЕРВАЯ ГРУППА
Продифференцируем
x
u
x
дважды по y и y
2 x
3u
;
y 2 y 2 x
v
y
2 y
3v
.
x 2 x 2 y
Складывая оба выражения почленно, получим:
2
2
2 x y
2 u v xy
2
2
y
x
x y y x x y
Остальные два условия первой группы аналогично
дважды по x,
27.
ВТОРАЯ ГРУППАРассмотрим относительные сдвиги
Продифференцируем каждую зависимость по недостающей в обозначении
координате:
Составим следующее выражение
После дифференцирования по координате z, по той же, что и перемещение,
стоящее справа, получаем
Остальные аналогично
28.
Итого имеем:ПЕРВАЯ ГРУППА
2
2
2 x y xy
2
,
y 2
x
x y
2 y
2
2 z yz
2
,
z 2
y
y z
2 z 2 x 2 zx
2
,
x 2
z
z x
ВТОРАЯ ГРУППА
2 x
xz yx zy
2
,
x y
z
x
y z
2 y
yx zy xz
2
,
y z
x
y
z x
zy xz yx
2 z
2
.
z x
y
z
x y
29. 6. Закон Гука
При рассмотрении простейшего напряженного состояния – растяжения, еслинапряжение σ не превышает определенной величины - предела упругости, то
зависимость между напряжением и деформацией ε оказывается линейной
Е - модуль упругости материала (модуль Юнга), справочная
величина, характеристика материала.
Кроме продольной деформации – вытягивания, происходит поперечная
деформация, сужение стержня. Зависимости между продольной и поперечной
деформациями имеют вид
μ- коэффициент Пуассона (характеристика
материала), равная отношению поперечной
деформации к продольной.
30.
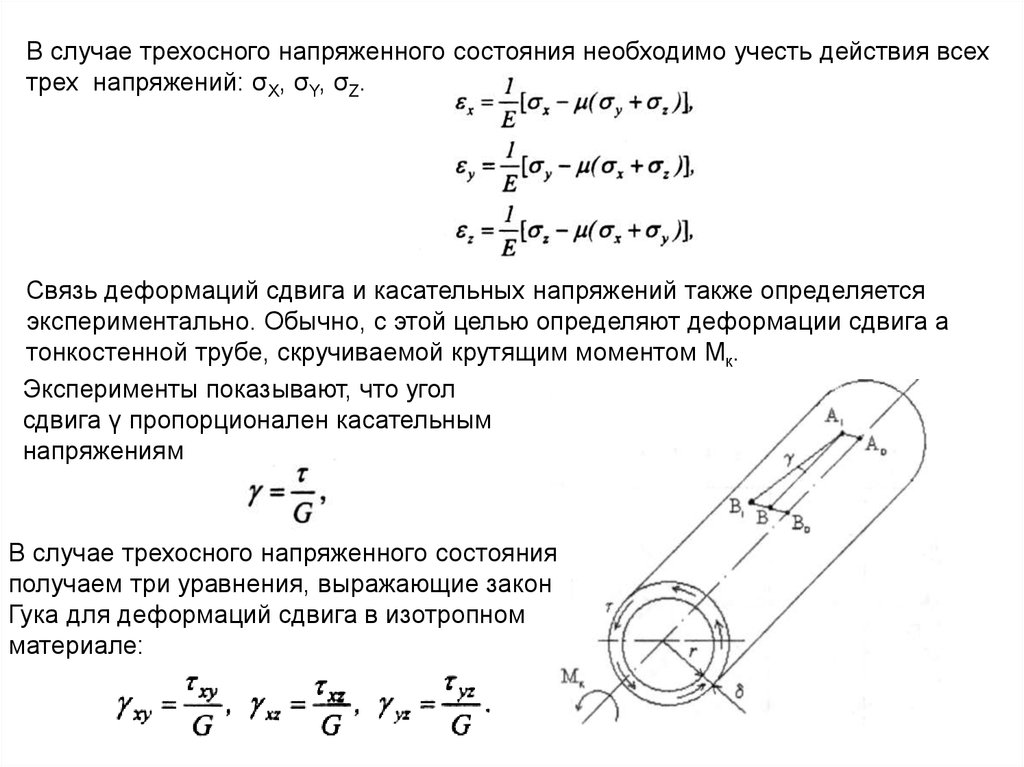
В случае трехосного напряженного состояния необходимо учесть действия всехтрех напряжений: σX, σY, σZ.
Связь деформаций сдвига и касательных напряжений также определяется
экспериментально. Обычно, с этой целью определяют деформации сдвига а
тонкостенной трубе, скручиваемой крутящим моментом Мк.
Эксперименты показывают, что угол
сдвига γ пропорционален касательным
напряжениям
В случае трехосного напряженного состояния
получаем три уравнения, выражающие закон
Гука для деформаций сдвига в изотропном
материале:
31.
Если дополнительно учесть эффект температурного удлинения материала то врезультате имеем
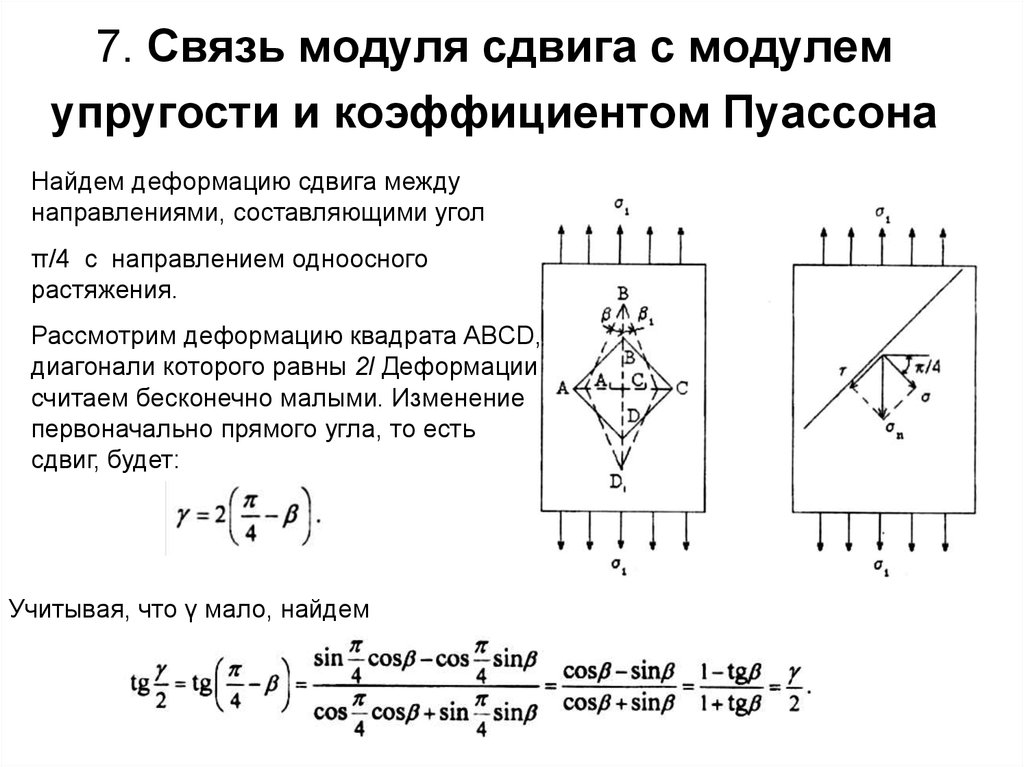
32. 7. Связь модуля сдвига с модулем упругости и коэффициентом Пуассона
Найдем деформацию сдвига междунаправлениями, составляющими угол
π/4 с направлением одноосного
растяжения.
Рассмотрим деформацию квадрата ABCD,
диагонали которого равны 2l Деформации
считаем бесконечно малыми. Изменение
первоначально прямого угла, то есть
сдвиг, будет:
Учитывая, что γ мало, найдем
33.
Деформация растяжения в продольном направлении равна ε1, а поперечнаядеформация сжатия με1. Поэтому
Следовательно:
По наклонной площадке действует касательное напряжение
По закону Гука
Сопоставляя 2 и 4 равенства
34. 8. Уравнения динамики твердого линейно-деформируемого тела
8. Уравнения динамики твердого линейнодеформируемого телаВ основе уравнений динамики линейно-деформируемого тела лежит второй закон
Ньютона:
F ma
Вырежем из тела, находящегося под действием системы сил бесконечно малый
элемент с ребрами dx, dy, dz.
На элемент действуют со стороны остального тела поверхностные силы – силы
упругости и объемные силы, как и на все точки тела.
Объемные силы, действующие на элемент могут
быть определены как произведение объемной
интенсивности на объем элемента
P3
z
FОБ K dV
Или проецируя по осям координат:
FОБx K y dV
FОБy K y dV
FОБz K z dV
P2
x
y
P1
35.
Действие сил упругости характеризуется нормальными и касательныминапряжениями действующими по граням элемента.
В силу малости размеров элемента можно считать, что изменение напряжений
вдоль ребер элемента происходит по линейному закону. В этом случае если на
левую грань действует напряжение σx, то на правую будет действовать
x x x tg dx
x
x
dx
x
ZX
σ
z
ZX
dz
z
Z
Z
dz
z
ZX
ZX
dz
z
XZ
dy
dx
σx+Δσx
σx
dz
α
dx
Δσx
XY
X
XZ
x
Аналогичные выражения можно
написать для остальных
компонентов тензора напряжений
y
Y
YХ
ZХ
Y
dy
y
Y
XY
YZ
X
ZY
YX
Z
YZ
XZ
dx
x
XY
dx
x
X
dx
x
YX dy
y
YZ
dy
y
x
36.
Таким образом, на левую грань элемента будет действовать сила упругостиопределяемая нормальным напряжением σх, и равная σхdydz. (dydz – площадь
грани).
На правую грань элемента будет действовать сила равная
X
dx dydz
X
x
Равнодействующая этих двух сил
X
X
X
dx dydz X dydz
dxdydz
dV
X
x
x
x
где dV – объем элемента
Вдоль оси x действуют так же компоненты тензора напряжений τyx (по дальней
грани) и τzx (по нижней грани). Проведя для них подобные выкладки получим
равнодействующие сил равные
ух
у
dV
и
zх
dV
z
Полная равнодействующая сил упругости вдоль оси х
ух
х
dV
dV zх dV
x
у
z
37.
Аналогично для осей у и z равнодействующие сил упругости равныхy
x
dV
y
y
yz
dV
zy
z
dV
хz
z
dV
dV
dV
x
y
z
Ускорение элемента выражаем как вторую производную по времени от
перемещения в направлении соответствующей оси:
2u
t 2
2v
t 2
2w
t 2
-вдоль оси х
-вдоль оси y
-вдоль оси z
Массу элемента определяем как произведение плотности на объем ρdV
38.
Собираем уравненияух
х
zх
2u
dV
dV
dV K x dV dV 2
x
у
z
t
хy
y
zy
2v
dV
dV
dV K y dV dV 2
x
y
z
t
yz
хz
z
2w
dV
dV
dV K z dV dV 2
x
y
z
t
Сокращаем на dV и переносим все налево
х ух zх
2u
Kx 2 0
x
у
z
t
хy y zy
2v
Ky 2 0
x
y
z
t
хz yz z
2w
Kz 2 0
x
y
z
t
Эти уравнения называются уравнениями динамики деформируемого тела.






























 Механика
Механика








