Механика материалов. Лекция 2. Основы теории напряженного и деформированного состояний

1.

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТРАНСПОРТА
кафедра «Локомотивы»
МЕХАНИКА МАТЕРИАЛОВ
Лектор: к.т.н., доцент Комиссаров Виктор Владимирович
Форма контроля знаний – экзамен
(по всем вопросам обращаться в ауд. 1410)
ГОМЕЛЬ, 2022

2.

ТЕМА 2
ОСНОВЫ ТЕОРИИ
НАПРЯЖЕННОГО
И
ДЕФОРМИРОВАННОГО
СОСТОЯНИЙ

3.

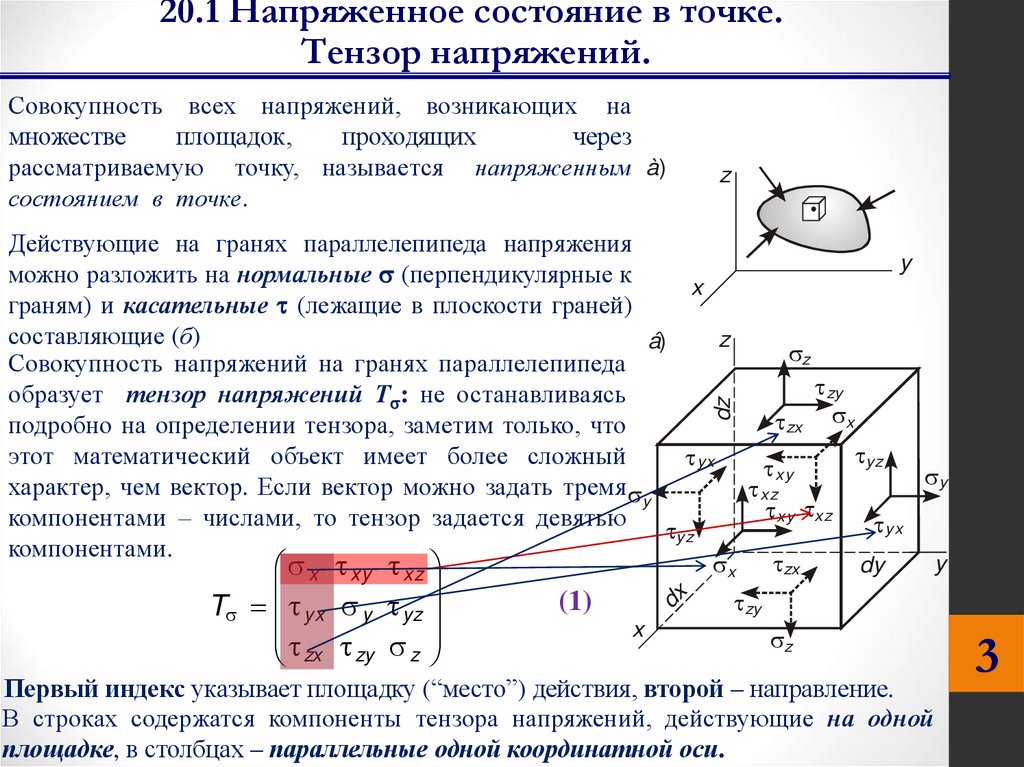
20.1 Напряженное состояние в точке.
Тензор напряжений.
Совокупность всех напряжений, возникающих на
множестве
площадок,
проходящих
через
рассматриваемую точку, называется напряженным à)
состоянием в точке.
z
dx
dz
Действующие на гранях параллелепипеда напряжения
y
можно разложить на нормальные (перпендикулярные к
x
граням) и касательные (лежащие в плоскости граней)
составляющие (б)
z
á)
z
Совокупность напряжений на гранях параллелепипеда
zy
образует тензор напряжений Т : не останавливаясь
zx x
подробно на определении тензора, заметим только, что
yz
этот математический объект имеет более сложный
yx
xy
y
характер, чем вектор. Если вектор можно задать тремя y
xz
xy xz
компонентами – числами, то тензор задается девятью
yx
yz
компонентами.
y
zx
x
dy
x xy xz
(1)
zy
T yx y yz
x
z
zx
zy
z
Первый индекс указывает площадку (“место”) действия, второй – направление.
В строках содержатся компоненты тензора напряжений, действующие на одной
площадке, в столбцах – параллельные одной координатной оси.
3

4.

20.1 Напряженное состояние в точке
Напряжения – мера, характеризующая распределение внутренних сил по
сечению.
Поскольку внутренние силы, представляют собой поверхностные силы, приложенные
R
к поперечному сечению оставленной части, то интенсивность этих сил, называемое
p lim
A 0 A
полным напряжением, определяется как указано ранее:
Размерность этого напряжения совпадает с размерностью поверхностной нагрузки
(Н/м2, МПа = 106 Н/м2).
Полное напряжение, как и равнодействующая внутренних сил, приложенных на элементарной
площадке, является векторной величиной и может быть разложено на две составляющие:
перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к
площадке – касательное напряжение n:
y
p
Касательное напряжение, в свою очередь, может быть разложено на
две составляющие, параллельные координатным осям x, y, связанным с
поперечным сечением - nx , ny :
При анализе напряжений в окрестности рассматриваемой точки
выделяется бесконечно малый объемный элемент (параллелепипед со
сторонами dx, dy, dz), по каждой грани которого действуют, в общем
случае, три напряжения, например, для грани, перпендикулярной оси x
ny
n
nx
σn
z
x
(площадка x) – σx, xy, xz :
Компоненты напряжений по трем
x yx zx
перпендикулярным граням элемента образуют
T
xy
y
zy
систему напряжений, описываемую так
называемым тензором напряжений:
xz yz z
Здесь первый столбец представляет компоненты напряжений на
площадках, нормальных к оси x, второй и третий – к оси y и z
соответственно.
σy
y
zy
yz
yx
xy
σz
z
zx
xz
x
σx
4

5.

20.1 Напряженное состояние в точке
Связь внутренних усилий и напряжений – Внутренние усилия в сечении связаны
уравнениями равновесия с внешними силами, приложенными к оставленной части бруса при его
сечении. С другой стороны внутренние усилия есть результат приведения к центру поперечного
сечения внутренних сил, приложенных к элементарным площадкам (напряжений), выполняемое
сложением, которое для элементарных сил сводится к интегрированию по площади поперечного
сечения.
Выполнение этой операции для каждого из внутренних усилий приводит к следующим
интегральным выражениям:
N z dA;
y
My
A
zy
Qx zx dA; Q y zy dA;
A
σz Qyx ΔА
A
z
M x z ydA; M y z xdA;
A
zx
Mz
N
O
y
Qx
Mx
A
x
M z ( zy x zx y ) dA.
A
Таким образом, в целом связь внешних сил, внутренних усилий и напряжений такова:
Внешние силы
Внутренние усилия
Уравнения равновесия
Напряжения
Интегральные соотношения
5

6.

20.2 Напряженное состояние в точке
Теорема парности касательных напряжений.
Из уравнения равновесия моментов сил относительно оси x
следует
yz dx dz dy – zy dx dy dz = 0,
отсюда yz = zy.
Составляя аналогичные уравнения относительно осей y и z,
получим, что xy = yx, zx = xz. Этот результат носит название
теоремы парности касательных напряжений: одноименные
касательные напряжения, действующие на двух взаимно
перпендикулярных площадках, равны по величине и
одновременно направлены либо к общему ребру, либо от него.
Следствие. Матрица тензора напряжений (1) симметрична
относительно своей главной диагонали. Независимыми в ней
являются шесть компонент: σx, σy, σz, τxy, τyz, τzx.
8

7.

;
20.2 Напряжения на произвольной площадке
à)
Пусть нормаль к площадке составляет с осями координат
углы, косинусы которых обозначим l, m, n:
z
dz
cos( , x ) l ; cos( , y) m ; cos( , z) n .
Для них выполняется известное из геометрии условие
dx
y
Величины l, m, n называются направляющими косинусами
нормали .
x
dy
l 2 + m 2 + n 2 = 1.
z
á)
xy x
xz
yx
y
yz
zy
x
Площадь косой площадки обозначим A. Площади
координатных граней Ax, Ay, Az (индекс указывает нормаль к
площадке) связаны с A следующими соотношениями:
A x Al ; A y Am ; A z An .
p z
p
p x
zx
z
p y
(2)
(3)
Проекции вектора полного напряжения p на косой
площадке обозначим p x, p y, p z.
y
p x A x Ax yx Ay zx Az 0
p y A xy Ax y Ay zy Az 0
p z A xz Ax yz Ay z Az 0
9
(4)

8.

;
20.2 Напряжения на произвольной площадке
p x x l yx m zx n
p y xy l y m zy n
p z xz l yz m z n
(5)
Модуль полного напряжения на площадке p p 2x p 2y p 2z
Таким образом, с помощью компонентов тензора напряжений
на трех координатных площадках можно полностью описать
напряженное состояние в точке, т. е. определить напряжения
на любой площадке, проведенной через рассматриваемую
точку.
10

9.

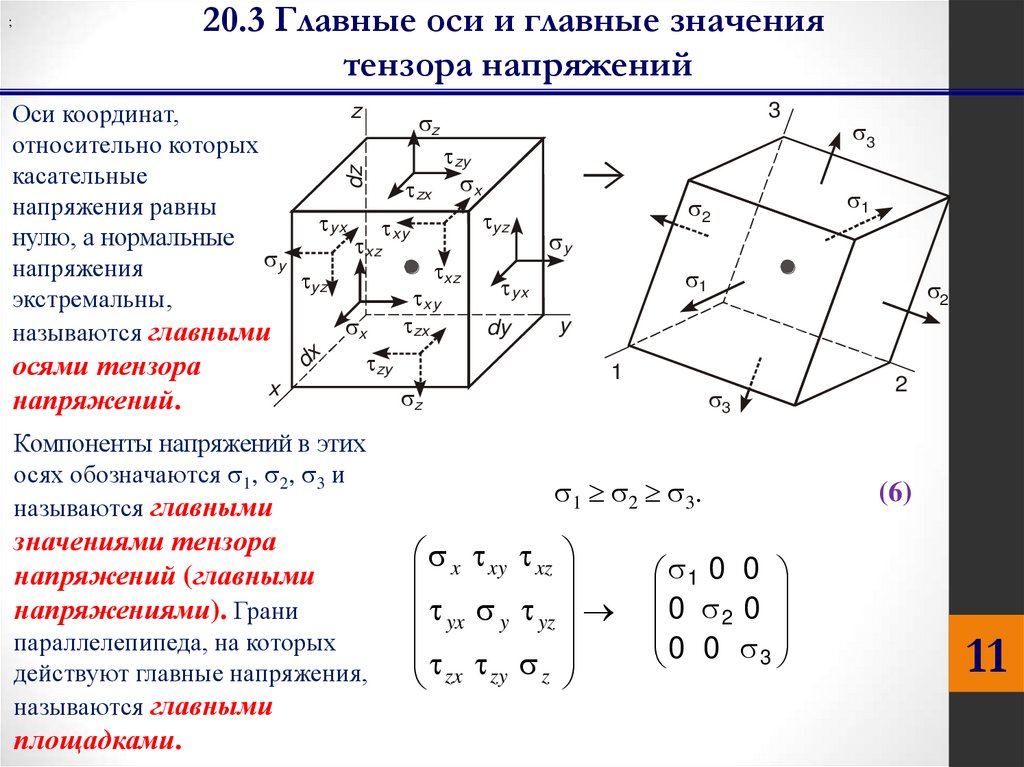
20.3 Главные оси и главные значения
тензора напряжений
;
z
Оси координат,
z
относительно которых
zy
касательные
zx x
напряжения равны
yz
yx xy
нулю, а нормальные
y
xz
y
напряжения
xz
yz
yx
xy
экстремальны,
y
zx
x
dy
называются главными
осями тензора
напряжений.
dx
dz
3
zy
x
Компоненты напряжений в этих
осях обозначаются 1, 2, 3 и
называются главными
значениями тензора
напряжений (главными
напряжениями). Грани
параллелепипеда, на которых
действуют главные напряжения,
называются главными
площадками.
z
2
3
1
1
2
1
3
1 2 3 .
x xy xz
yx y yz
zx zy z
1 0 0
0
0
2
0 0 3
2
(6)
11

10.

;
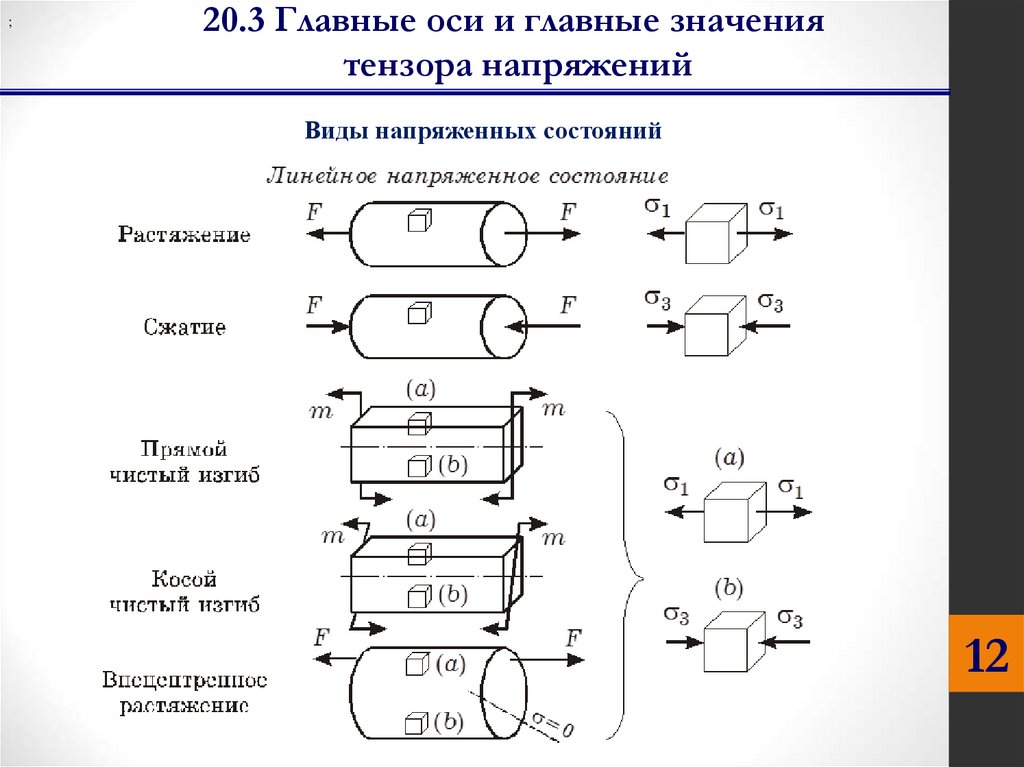
20.3 Главные оси и главные значения
тензора напряжений
Виды напряженных состояний
12

11.

;
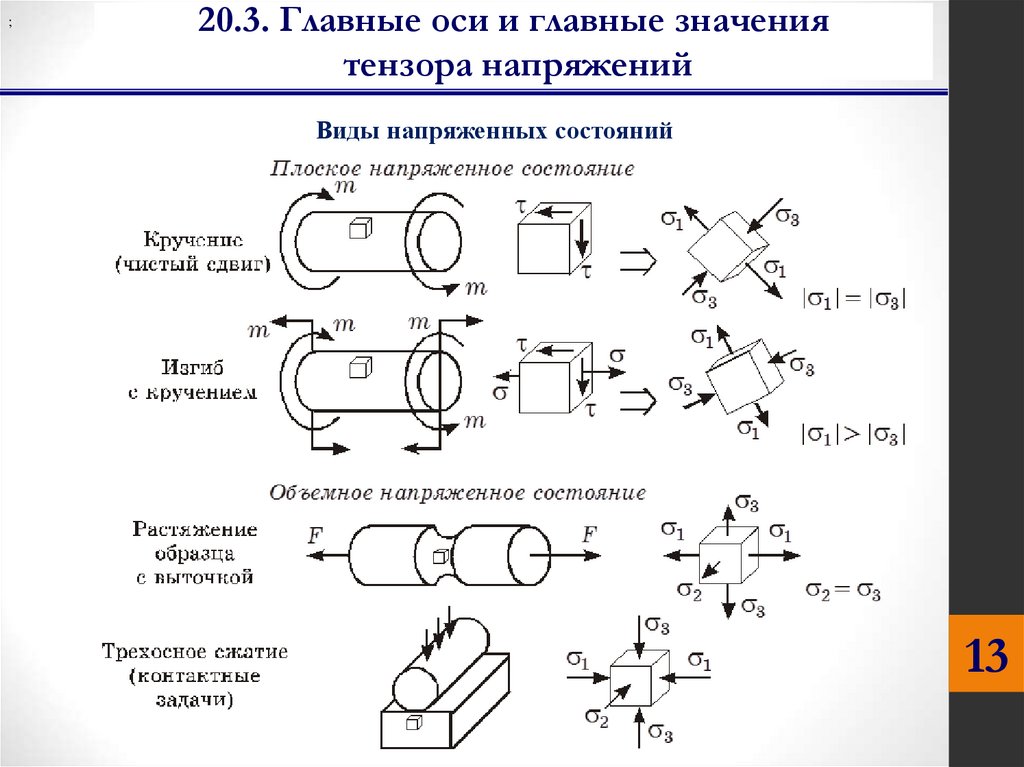
20.3. Главные оси и главные значения
тензора напряжений
Виды
напряженных
Виды
напряженныхсостояний
состояний
13

12.

20.4. Вычисление главных значений тензора
напряжений
;
z
p x = l; p y = m; p z = n.
Подставив их в соотношения (5), выражающие проекции
полного напряжения на косой площадке через
координатные напряжения, получим
p
l = x l + yx m + zx n;
m = xy l + y m + zy n;
n = xz l + yz m + z n.
y
x
Отсюда
( x – )l + yx m + zx n = 0;
xy l + ( y – )m + zy n = 0;
xz l + yz m + ( z – )n = 0.
(7)
Нулевое решение l = m = n = 0 не имеет физического смысла, так как не
выполняется условие (2) l2 + m2 + n2 = 1. Для существования ненулевого решения
необходимо и достаточно, чтобы определитель системы (7) был равен нулю:
x
xy
xz
yx
y
yz
zx
zy
z
0
14
(8)

13.

;
;
20.4. Вычисление главных значений тензора
напряжений
ОПРЕДЕЛЕНИЕ ВЕЛИЧИН ГЛАВНЫХ НАПРЯЖЕНИЙ.
Раскрывая определитель (8), получаем следующее кубическое уравнение
относительно нормального напряжения на главной площадке:
3 J1 2 J 2 J 3 0
(9)
Уравнение (9) называется вековым. Здесь коэффициенты
J1 = x + y + z;
J2 = x y + y z + z x – 2xy 2yz 2zx ;
x
xy xz
J 3 yx y yz x y z 2 xy yz zx x 2yz y 2zx z 2xy .
zx zy
(10)
z
Так как все три корня 1, 2, 3 (главные значения тензора напряжений) уравнения
(9) вещественные, то их величины определяются характером внешней нагрузки и
не зависят от ориентации первоначальной системы координат x, y, z.
Следовательно, и коэффициенты уравнения (9), от которых зависят значения 1, 2,
3, инвариантны к выбранной системе декартовых осей, т. е. при повороте осей
не изменяются:
J = const; J = const; J = const.
1
2
3
Их называют первым, вторым и третьим инвариантами тензора напряжений.
15

14.

;
;
20.4. Вычисление главных значений тензора
напряжений
СЛЕДСТВИЕ
Поскольку корни кубического уравнения (9) равны 1, 2, 3, то его можно
записать также в виде
( 1 )( 2 )( 3 ) 0
J1 = 1 + 2 + 3, J2 = 1 2 + 2 3 + 3 1, J3 = 1 2 3
Значения инвариантов тензора напряжений, выраженные через главные
напряжения
16

15.

20.5. Напряжения на октаэдрических площадках
Формулы для напряжений на произвольной площадке значительно упрощаются,
если в качестве исходного выбрать элементарный параллелепипед, ограниченный
главными площадками.
В соответствии с формулами (5) получаем
à)
á)
3
p 1 = 1l; p 2 = 2m; p 3 = 3n. (11)
3
1
p 3
2
(l , m, n)
2
p
2
3
p
p 2
p 1
1
1
1
3
Оставим в соотношениях (11) справа
косинусы нормали к косой площадке
l, m, n и возведем все в квадрат.
После этого просуммируем левые и
правые части по отдельности.
2 Учитывая выражение (2) для суммы
квадратов косинусов, получим:
2
2
2
p 1 p 2 p 3
1
1 2 3
СЛЕДСТВИЕ. Полученному уравнению можно дать наглядное толкование. Если
величины p 1, p 2, p 3 рассматривать как координаты конца вектора полного
3
напряжения p , возникающего на произвольно ориентированной
площадке, возникающего на произвольно ориентированной
3 p
площадке, то геометрическое место концов этого вектора
1
2
образует эллипсоид напряжений. Полуосями его являются
2
главные напряжения 1, 2, 3.
1
17

16.

20.5. Напряжения на октаэдрических площадках
Модуль, нормальная и касательная составляющие вектора
Разложим вектор p на нормальную и касательную составляющие
p 2 2 2 .
Тогда модуль вектора напряжения на произвольной площадке
:
p
(12)
p 21 p 22 p 23 12l 2 22 m2 32 n2 .
Нормальное напряжение получим как сумму проекций составляющих полного
напряжения на нормаль
p 1l p 2 m p 3n 1 l 2 2 m2 3n 2 .
(13)
Подставляя последние два выражения для pν и σν в (12) и учитывая, что l2 + m2 +
+ n2 = 1, получим величину касательных напряжений на произвольной площадке
( 1 2 )2 l 2 m2 ( 2 3 )2 m2 n2 ( 1 3 )2 n2l 2 .
(14)
СЛЕДСТВИЕ: При изучении сложного деформирования брусьев с учетом
пластических деформаций оказывается важным знать напряжения на площадках,
равнонаклоненных к главным осям тензора напряжений. Такие площадки
называются октаэдрическими, так как они параллельны грани октаэдра,
образованного из куба.
Нормаль к октаэдрической площадке образует равные углы с главными осями,
следовательно, ее направляющие косинусы одинаковы: l2 = m2 = n2 = 1/3.
Подставив эти значения в формулы (13), (14), получим нормальные и
касательные напряжений на октаэдрической площадке:
18

17.

20.5. Напряжения на октаэдрических площадках
oct 13 1 2 3 ;
oct 13
( 1 2 ) ( 2 3 ) ( 1 3 ) .
2
2
2
(15)
Октаэдрические напряжения являются инвариантными величинами и
выражаются через инварианты тензора напряжений
oct 13 J1; oct 13 2 J12 2 J 2 .
19

18.

20.5.1 Максимальные касательные напряжения
Особый интерес представляют площадки, на которых
возникают максимальные касательные напряжения.
Положение этих площадок можно определить, исследуя
выражение (14). ( 1 2 )2 l 2 m2 ( 2 3 )2 m2 n2 ( 1 3 )2 n2l 2 .
Заметим, что 1 2 3 и максимальной разностью в (14)
будет σ1 – σ3, которую запишем в виде σ1 – σ3 = (σ1 – σ2) + (σ2 –
σ3).Так как квадрат числа не меньше суммы квадратов чисел, его
составляющих, то (σ1 – σ3)2 ≥ (σ1 – σ2)2 + (σ2 – σ3)2.
Чтобы величина τν достигла максимума, необходимо в (14)
увеличить большее из слагаемых. Это достигается ростом
произведения n2l2 за счет m2.
Максимум будет при m2 = 0, l2 = n2 = 1/2. Тогда
max 12 1 3 .
(16)
20

19.

20.5.1 Максимальные касательные напряжения
Следовательно:
площадка с максимальным касательным напряжением
равнонаклонена к площадкам, на которых действуют
максимальное 1 и минимальное 3 из главных напряжений,
и параллельна оси 2.
3
45о
о
45
1
2
21

20.

20.6 Плоское напряженное состояние
В случае плоского напряженного состояния в точке все
напряжения на одной из координатных плоскостей равны нулю.
Например, если σz = τzx = τzy = 0, то по оси z напряженное
состояние элементарного параллелепипеда не изменяется (рис.
y
y
á)
а).à)
б)
z
à)
á)
z
yx
y
x
dy
dx
x
y
x
xy
x
x
dy
dz
yx
xy
dy
xy
yx
y
dx
y
yx
y
y
dy
y
yx
y
xy xy
dx
yx
dz
xy
x
y
yx
x
x
x
xy
x
x
Поэтому в дальнейшем вместо объемного
элемента будем рассматривать плоскую
прямоугольную координатную площадку с
размерами dx, dy, на которой действуют
напряжения σx, σy, τxy (рис. б).
x
xy
dx
y
yx
22

21.

20.6. Плоское напряженное состояние
Главные напряжения.
Здесь ось z является главной, так как на соответствующей
площадке все касательные напряжения равны нулю. Поэтому
можно принять σ2 = σz = 0, предполагая, что напряжения σ1, σ3
имеют разные знаки.
Для их вычисления воспользуемся вековым уравнением (9).
3 J1 2 J 2 J 3 0
Инварианты тензора напряжений (10) принимают значения
J1 = x + y;
J2 = x y – 2xy ;
J3 = 0.
и кубическое уравнение (9) сводится к квадратному
2 – (
2
x + y) + ( x y – xy ) = 0.
23

22.

20.6. Плоское напряженное состояние
Корни этого уравнения являются главными значениями
тензора напряжений при плоском напряженном состоянии
x y 1
1,3
( x y )2 4 2xy .
(17)
2
2
Главные площадки.
A ( x sin xy cos )A x ( y cos yx sin )A y 0
y
yx
y
Отсюда, сокращая на A, получим
( x sin xy cos )cos ( y cos yx sin )sin .
Ay
Выполняя преобразования получим
Ax
x
x y
A
x
21 ( x y ) sin 2 xy cos2
24

23.

20.6 Плоское напряженное состояние
На
главной
площадке
касательные
напряжения
обращаются в нуль.
Предположив, что рассматриваемая косая площадка
является главной, и положив в последней формуле τα = 0,
получим
tg 2
2 xy
y x
.
(18)
25

24.

(dy )
20.7 Деформированное состояние в точке
y
dy
Проведем
через
рассматриваемую
точку
тела
сечение и возьмем в его плоскости
прямоугольник (см. рисунок) с
взаимно
перпендикулярными
элементами dx, dy.
Через Δ(dx), Δ(dy) обозначим
изменения длин волокон,
а
через α, β – углы их поворота
x после приложения нагрузки.
(dx ) Тогда угловой γху и линейными
dx
εx, εy
деформациями будут
εx =
следующие величины:
d
26
(dy )
(dx )
εx = lim
; εy = lim
; γx y = l i m ( ) .
dx 0
dx 0 dx
dy 0 dy
dy 0

25.

20.7 Деформированное состояние в точке
Совокупность всех деформаций εx, εy, εz, γxy, γyz, γzx
полностью описывает деформированное состояние в точке
тела, т. е. по этим шести компонентам можно найти
удлинение любой оси и углы сдвига в любых плоскостях,
проходящих через рассматриваемую точку.
Эти величины образуют тензор деформаций Тε, матрица
которого записывается в виде
x
1
T 2 yx
1
2 zx
1
2 xy
y
1
2 zy
1
2 xz
1
2 yz .
z
27

26.

20.7. Деформированное состояние в точке
Главные значения тензора деформаций.
1 0 0
T 0 2 0
0 0
3
где ε1, ε2, ε3 – главные значения тензора деформаций
(главные деформации).
Их величины вычисляются как корни кубического уравнения,
аналогичного вековому уравнению тензора напряжений (9):
I 1 I 2 I 3 0
3
2
где I1, I2, I3 – инварианты тензора деформаций:
28

27.

20.7. Деформированное состояние в точке
I 1 x y z
I 2 x y y z z x 14 2xy 14 2yz 14 2zx
x
I 3 21 yx
1
2 zx
1
2 xy
y
1
2 zy
1
2 xz
1
2 yz
z
В главных осях они принимают вид:
I 1 1 2 3
I 2 1 2 2 3 3 1
I 3 1 2 3
29

28.

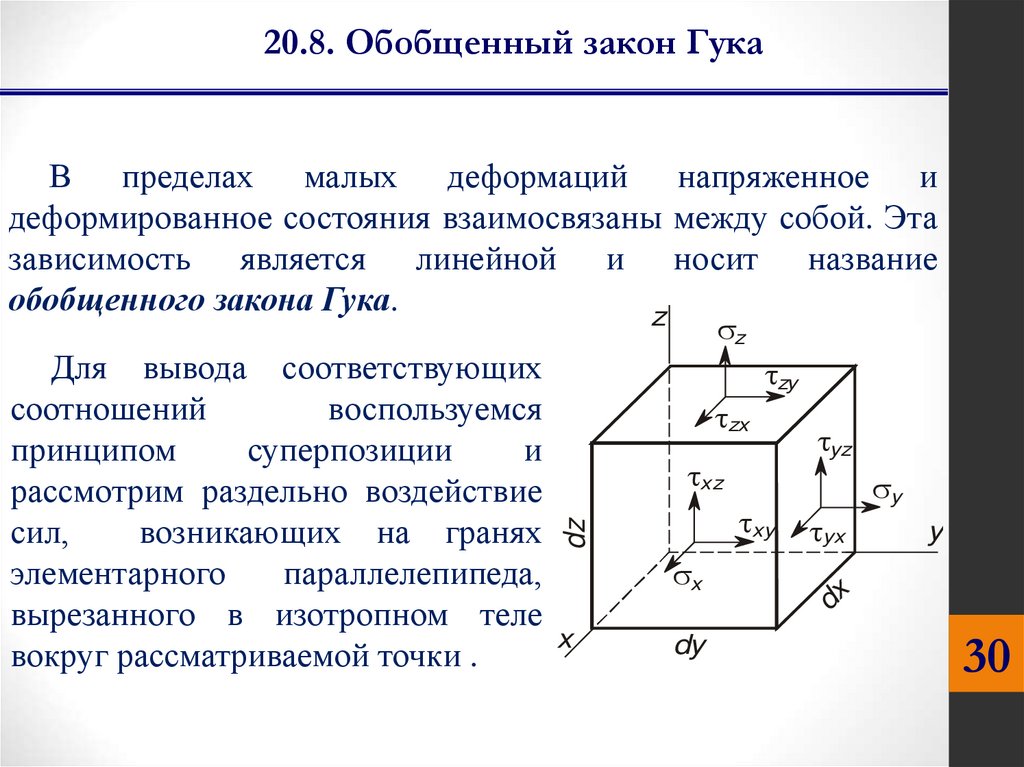
20.8. Обобщенный закон Гука
В пределах малых деформаций напряженное и
деформированное состояния взаимосвязаны между собой. Эта
зависимость является линейной и носит название
обобщенного закона Гука.
z
zy
xz
xy
x
dy
yz
y
yx
y
dx
zx
dz
Для вывода соответствующих
соотношений
воспользуемся
принципом
суперпозиции
и
рассмотрим раздельно воздействие
сил,
возникающих на гранях
элементарного
параллелепипеда,
вырезанного в изотропном теле
x
вокруг рассматриваемой точки .
z
30

29.

20.8. Обобщенный закон Гука
Направление
деформации
x
Относительные деформации
ε и ε' от действия нормальных напряжений
σx
σy
x
E
y
z
x
E
x
E
σz
y
E
y
E
y
E
z
E
z
E
z
E
Сложив все деформации одного направления, получают
y
x
z
x
.
E
E
E
31

30.

20.8. Обобщенный закон Гука
32
εx = 1 x y z ;
E
εy = 1 у z x ;
E
(19)
εz = 1 z x y .
E
x y = Gγx y ; yz = Gγyz; zx = Gγzx .
Полученные соотношения (19), (20) являются
аналитическим выражением обобщенного закона Гука
для изотропного тела.
(20)
32

31.

20.9. Объемная деформация
z
z
zy
zx
xz
yz
y
Линейные размеры элементарного
параллелепипеда dx, dy, dz, взятого
вокруг точки, в результате
деформирования изменяются и
становятся:
dz
dx + Δ(dx ) = dx + εx dx = dx (1+ εx );
y
dx x+ Δ(dx ) = dx + εx dx = dx (1+ εx ); dy(1+ εy ); dz(1+ εz).
x
d
+ Δ(dx ) = dx + εx dx = dx (1+ εx ); dy(1+ εy ); dz(1+ εz).
x
dy
xy
yx
dy(1
Абсолютное приращение объема вычисляется как разность
между новым и старым объемом:
V dx(1 x ) dy(1 y ) dz(1 z ) dx dy dz.
V dx dy dz( x y z ).
33

32.

20.9. Объемная деформация
34
Отношение приращения V к первоначальному объему
параллелепипеда V называется объемной деформацией θ.
V dx dy dz ( x y z )
x y z .
V
dx dy dz
(21)
Выражение объемной деформации через нормальные
напряжения получим, подставив в формулу (21) соотношения
обобщенного закона Гука (20):
1 2
x y z .
E
1 2
3
p.
E
(22)
34

33.

20.10. Полная потенциальная энергия
деформации
Определим работу, относящуюся к напряжению σx.
Соответствующая ему элементарная средняя сила
0,5 x dydz совершает работу на перемещении
Δ(dx) = εx dx.
Эта работа имеет величину
0,5 x dydz ∙εx dx .
Средняя касательная сила 0,5 τyz dz dx на перемещении γyz
dy совершает работу
0,5 τyz dz dx ∙γyz dy.
dU = 0,5 dx dy dz ( x εx + y εy + z εz + τxyγxy + τyzγyz +
τzxγzx)
35

34.

20.10. Полная потенциальная энергия деформации
Если энергию отнести к объему параллелепипеда dx dy dz и
с помощью закона Гука (19), (20) выразить деформации через
напряжения, получим удельную потенциальную энергию
единицы объема
(23)
U0
1
2x 2y 2z 2 x y y z z x
2E
1 2
xy 2yz 2zx
2G
Через главные напряжения удельная потенциальная энергия
(23) выражается в виде
1
U0
12 22 32 2 1 2 2 3 3 1
2E
(24)
Полную
потенциальную
энергию
получим, 36
проинтегрировав удельную потенциальную энергию (23), (24)
по объему деформированного тела.

35.

20.11. Потенциальные энергии изменения
объема и формы
Деление потенциальной энергии U0 на энергию изменения
объема Uv и энергию формоизменения Ud, т. е.
U0 = Uv + Ud,
является условным и потребуется в дальнейшем при изучении
предельных напряженных состояний.
Потенциальную энергию изменения объема получим как
работу среднего напряжения
13 x y z .
на объемной деформации θ.
1 2
Используя формулу (22), имеем
x y z .
E
37
1 2
1 2
2
2 (25)
U
или
U
.
x
y
z
1
2
3
6E
6E

36.

20.11. Потенциальные энергии изменения
объема и формы
Энергию формоизменения Ud = U0 – Uv найдем, используя
формулы (23) и (25).
После некоторых преобразований получим следующие
выражения в произвольной и главной системах координат:
1
1 2
2
2
2
Ud
( x y ) ( y z ) ( z x )
xy 2yz 2zx
6E
2G
1
Ud
( 1 2 )2 ( 2 3 )2 ( 3 1 )2
6E
(26)
В частном случае всестороннего равномерного растяжения
или сжатия 1 = 2 = 3 = p получим
Uv = 3 1 2 p 2 ;
2
E
Ud = 0.
38

37.

20.11. Потенциальные энергии изменения
объема и формы
При чистом сдвиге присутствуют только касательные
напряжения: x = y = 0, τxy = τ, или, согласно формуле (17)
σ1 = τ, σ2 = 0, σ3 = –τ.
Поэтому составляющие потенциальной энергии имеют вид
1 2
.
Uv = 0; Ud =
E
Сравнивая формулы (15) с (25), (26), легко заметить, что
энергия изменения объема и энергия формоизменения
пропорциональны соответственно квадратам нормального и
касательного напряжений на октаэдрических площадках.
oct 13 1 2 3 ;
oct 13 ( 1 2 ) ( 2 3 ) ( 1 3 ) .
2
2
2
(15)
39

38.

40