Консультация по физике

1. КОНСУЛЬТАЦИЯ ПО ФИЗИКЕ

Лубенченко О. И., кафедра физики им. В. А. Фабриканта
НИУ «МЭИ», 2020 г.

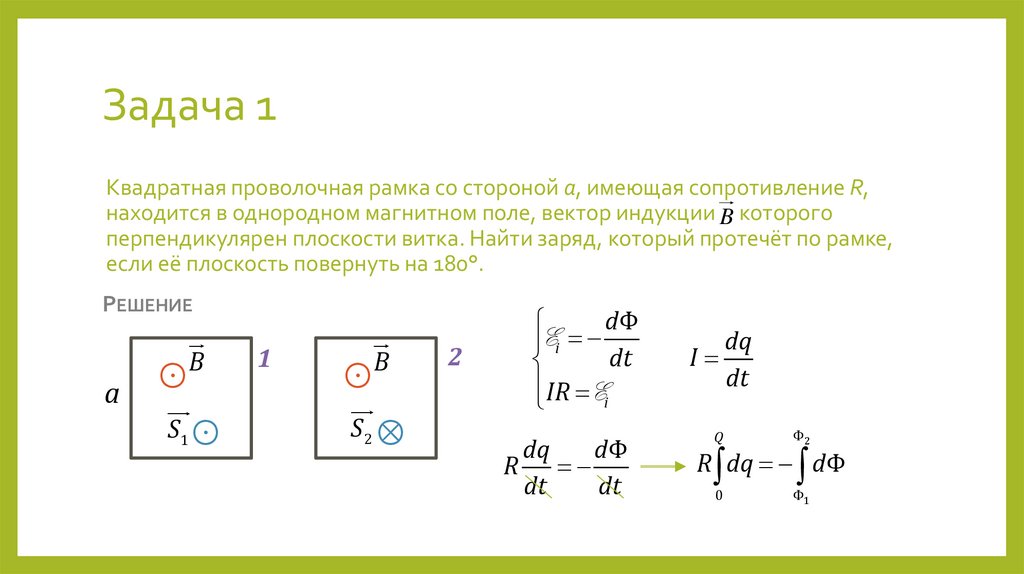
2. Задача 1

Квадратная проволочная рамка со стороной a, имеющая сопротивление R,
находится в однородном магнитном поле, вектор индукции B которого
перпендикулярен плоскости витка. Найти заряд, который протечёт по рамке,
если её плоскость повернуть на 180°.
РЕШЕНИЕ
a
B
⊙
S1 ⊙
1
B
⊙
S2 ⊗
2
dΦ
Ei
dt
IR Ei
dq
dΦ
R
dt
dt
I
dq
dt
Q
Φ2
0
Φ1
R dq dΦ

3. Задача 1

RQ Φ1 Φ2
Φ1 Φ2
Q
R
Φ1 BS1 BS cos0 BS Ba2 Φ2 BS 2 BS cos π BS Ba2 S a2
2
1
2Ba
Q Ba2 Ba2
R
R
2Ba2
Q
R

4. Задача 2

Участок провода, по которому идёт ток I, согнут в виде полуокружности
радиуса R. Найти индукцию магнитного поля, созданного этим участком в
центре полуокружности.
РЕШЕНИЕ
dl
I
R
dB
O
⊗
r
μ0 dl , r
B dB
dB
I 3
4π
r
π
μ0 Idl sin 2
μ0 I
dB
dl
2
2
4π R
4πR
μ0 I πR
μ0 I
μ0 I
B
dl
πR
2
2
4πR 0
4πR
4R
μ0 I
B
4R

5. Задача 3

Внутрь длинного соленоида поместили квадратную рамку с током. Ток в
соленоиде равен I, плотность намотки соленоида — n, ток в рамке — i, сторона
рамки — a. Нормаль к плоскости рамки составляет угол α с осью соленоида.
Найти момент сил, с которыми магнитное поле соленоида действует на рамку.
РЕШЕНИЕ
⊙I ⊙ ⊙ ⊙
B
⊙ α pm , S
i
a⊗ M⊗
⊗ ⊗ ⊗ ⊗
M pm , B pm iS
pm ia2 B μ0nI
M pm B sin α μ0na2Ii sin α
M μ0na2Ii sin α

6. Задача 4

При какой напряжённости электрического поля в вакууме объёмная плотность
энергии этого поля будет такой же, как у магнитного поля с индукцией 1,0 Тл
(тоже в вакууме)?
РЕШЕНИЕ
ε0E
we
2
2
B2
wm
2μ0
2
B
E2
c 2B 2
ε0 μ0
ε0E 2 B 2
2
2μ0
ЧИСЛЕННЫЙ РАСЧЁТ
В
E 3 10 1,0 3 10
м
8
8
E cB

7. Задача 5

По тонкому кольцу радиуса R идёт ток I. Найти магнитную индукцию в центре
кольца.
РЕШЕНИЕ
I
dl
R
dB
⊗
O
r
μ0 dl , r
B dB
dB
I 3
4π
r
π
μ0 Idl sin 2
μ0 I
dB
dl
2
2
4π R
4πR
μ0 I 2πR
μ0 I
μ0 I
B
dl
2πR
2
2
4πR 0
4πR
2R
μ0 I
B
2R

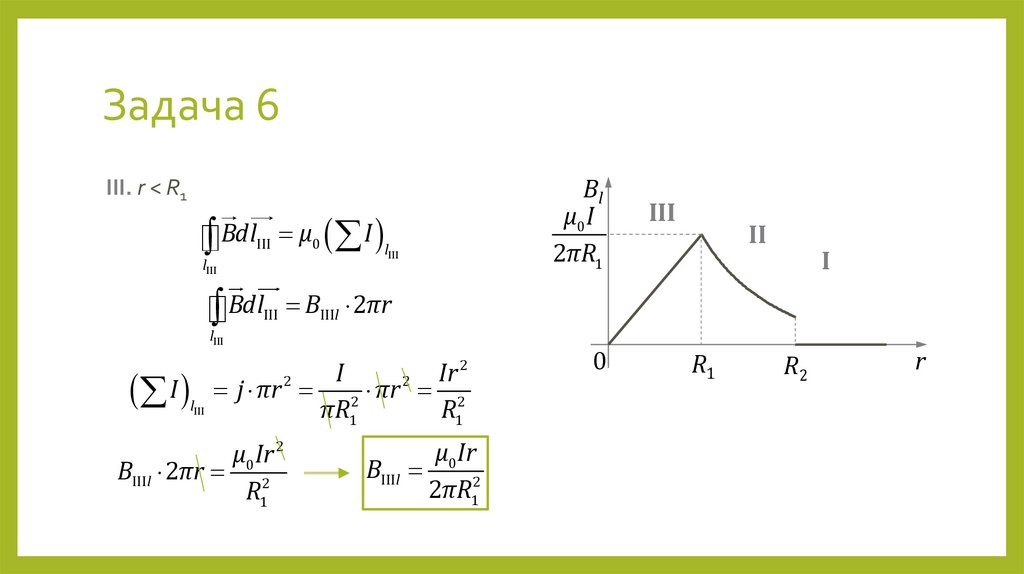
8. Задача 6

По коаксиальному кабелю идёт ток I. Внутренний провод — сплошной цилиндр
радиуса R1, внешний провод — полый цилиндр радиуса R2. Найти зависимость
магнитной индукции от расстояния r от оси кабеля. Считать плотность тока
постоянной по сечению внутреннего провода.
РЕШЕНИЕ
I. r > R2
Bdl
Теорема о циркуляции B
I
lI
Bdl B dl cos0 B dl
I
lI
Il
lI
I
Il
I
lI
μ0 I l
BIl 2πr
I
I
lI
I I 0
BIl 0

9. Задача 6

II. R1 < r < R2
Bdl
II
lII
Bdl
III
μ0 I l
II
II
I
BIIl 2πr
lII
I
lII
lII
I
BIIl 2πr μ0 I
μ0 I
BIIl
2πr
lI
lIII
R1
II
I
R2
I
⊗ dlII
r
⊗BII
C r
⊗dlIII
r ⊗B
III
D
⊗ dlI
⊗ BI
A

10. Задача 6

Bl
μ0 I
2πR1
III. r < R1
Bdl
III
lIII
μ0 I l
Bdl
III
III
lIII
2
I
Ir
j πr 2 2 πr 2 2
πR1
R1
μ0 Ir 2
BIIIl 2πr 2
R1
II
I
BIIIl 2πr
lIII
I
III
BIIIl
μ0 Ir
2πR12
0
R1
R2
r

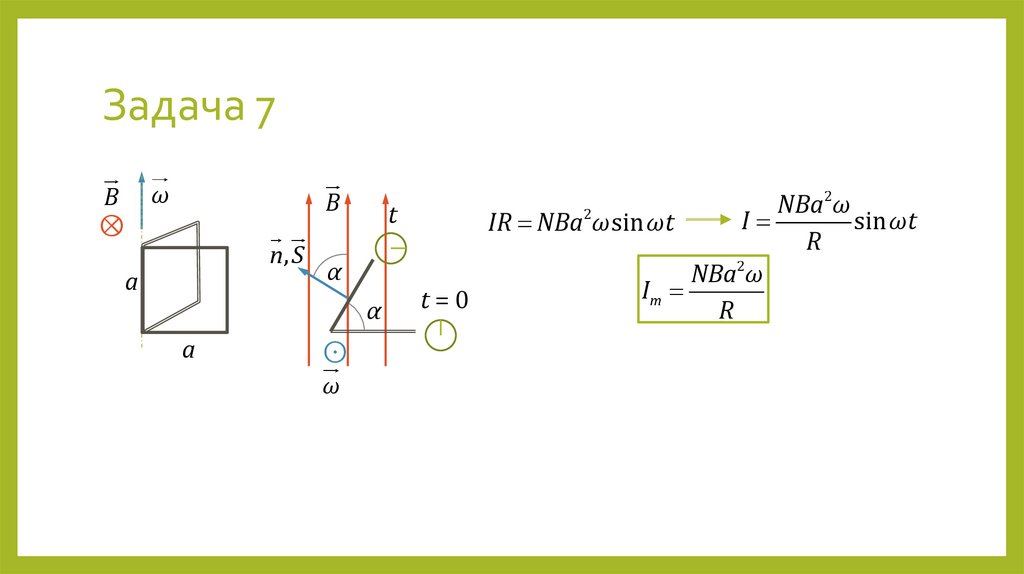
11. Задача 7

Квадратная рамка со стороной a, имеющая N витков и сопротивление R,
вращается в однородном магнитном поле с индукцией B вокруг одной из своих
сторон. Ось вращения рамки перпендикулярна вектору магнитной индукции.
Угловая скорость рамки постоянна и равна ω. Найти максимальное значение
тока в рамке.
РЕШЕНИЕ
dΦ
dt
α ωt
Закон Фарадея-Максвелла: Ei
S a2
Φ NBS NBS cos α
d
Ei
NBa2 cos ωt NBa2ω sin ωt
dt
Закон Ома: IR Ei

12. Задача 7

ω
B
⊗
B
2
NBa
ω
2
t
I
sin ωt
IR NBa ω sin ωt
R
n, S
α
NBa2ω
Im
t
=
0
R
α
a
a
⊙
ω

13. Задача 8

Электрон влетает в область, где существует однородное магнитное поле с
индукцией B. Начальная скорость электрона равна v и направлена
перпендикулярно линиям магнитной индукции. Найти параметры траектории
электрона.
РЕШЕНИЕ
II закон Ньютона: me a F2
⊙B
O
R
F2
a
⊝
e me
v
F2 e vB
π
me an evB sin
2
v2
an
R
v2
me evB
R
me v
R
eB

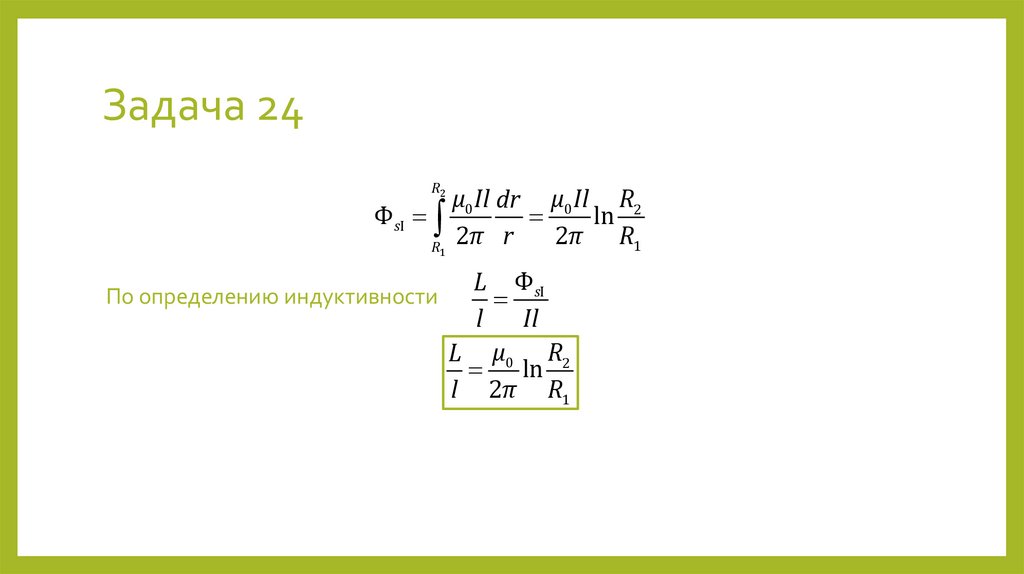
14. Задача 24

Найти индуктивность единичного участка коаксиального кабеля, у которого
радиус внутреннего проводника R1, а радиус внешнего проводника R2. Полем
внутри внутреннего проводника пренебречь.
II
РЕШЕНИЕ
I
I. R1 < r < R2
μ0 I
BI
2πr
R1
I
(см. решение задачи 6)
dΦsI BIdS I BIdS I cos0 BIdS I
μ0 Il dr
dΦsI
2π r
r
dS I ldr
I
R2
dr
l
⊗dS I
⊗BI

15. Задача 24

R2
μ0 Il dr μ0 Il R2
ΦsI
ln
2π r
2π R1
R1
По определению индуктивности
L ΦsI
l
Il
L μ0 R2
ln
l 2π R1

16. Задача 9

Тонкий стержень длиной l равномерно заряжен с линейной плотностью τ.
Найти напряжённость и потенциал электрического поля в точке, лежащей на
продолжении стержня на расстоянии a от его ближнего конца. Принять
потенциал равным нулю в бесконечно удалённой точке.
РЕШЕНИЕ
B τ, l
dq
dr
A
r
a
Принцип суперпозиции: E dE
E
O
dE
Поле точечного заряда
dq r
dE
4πε0 r 3

17. Задача 9

dq
dE
4πε0r 2
a l
E
a
dq τdr
τdr
dE
4πε0r 2
τdr
τ 1
τ 1
1 τ a l a
τl
2
4πε0r
4πε0 r a
4πε0 a a l 4πε0a a l 4πε0a a l
a l
E
τl
4πε0a a l
dq
Потенциал поля точечного заряда при φ(∞) = 0: dφ
4πε0r
Принцип суперпозиции: φ dφ

18. Задача 9

τdr
dφ
4πε0r
a l
φ
a
τdr
τ
τ
a l
a l
ln r a
ln
4πε0r 4πε0
4πε0
a
τ
a l
φ
ln
4πε0
a
Предельный случай
τl
q
a >> l: E
2
4πε0a 4πε0a2
— поле точечного заряда
τ
l
τl
q
φ
ln 1
4πε0
a 4πε0a 4πε0a

19. Задача 10

По тонкому полукольцу радиуса R равномерно распределён заряд Q. Найти
напряжённость и потенциал электростатического поля в центре полукольца.
Принять потенциал равным нулю в бесконечно удалённой точке.
РЕШЕНИЕ
dq
Q
R
dE
r
dα
O
α
y
E
Поле точечного заряда dE
dq r
4πε0 r 3
Принцип суперпозиции E dE
dq cos α
E E y dE y dE cos α
dq τdl dl Rdα
2
4πε0r
Q
r R
τ
πR

20. Задача 10

Q cos αdα
dE y
2
2
4
π
ε
R
π
0
π
2
Q
Q
Q
Q
2
E E y 2 2 cos αdα 2 2 sin α π 2 2 1 1 2 2
4π ε0R π
4π ε0R
4π ε0R
2π ε0R
2
2
Q
E 2 2
2π ε0R
dq
dφ
4πε0r
φ dφ
Q
dq
Q
φ
4πε0R 4πε0R
0
Q
φ
4πε0R

21. Задача 11, 14

По тонкому кольцу радиуса R равномерно распределён заряд Q. Найти
напряжённость и потенциал электростатического поля в точке, находящейся
на оси кольца на расстоянии z от его центра. Принять потенциал равным нулю
в бесконечно удалённой точке.
РЕШЕНИЕ
dq r
Принцип суперпозиции E dE
3
4πε0 r
dq
z
z
2
2
dE z
cos θ r R z cos θ
2
4πε0r
r
R2 z 2
Поле точечного заряда dE
E Ez
dE z
dq
dE
4πε0r 2
dq z
4πε0 R z
2
Q
2
32
Ez
0
dq z
4πε0 R z
2
2
32
Qz
4πε0 R z
2
2
32

22. Задача 11, 14

z
E
dE
dE
E
Qz
4πε0 R z
2
2
32
Потенциал поля точечного заряда dφ
dq
4πε0r
A
Принцип суперпозиции φ dφ
r θ r
Q
dq
dq
Q
dq′
Q
dφ
φ
z R
2
2
2
2
4πε0 R z
4πε0 R 2 z 2
0 4πε0 R z
O
Q
dq
φ
4πε0 R 2 z 2

23. Задача 11, 14

Предельные случаи
Q
1) z = 0: E 0 φ
4πε0R
Qz
Q — поле точечного заряда
2) z >> R: E
3
4πε0 z
4πε0 z 2
Q
φ
4πε0 z

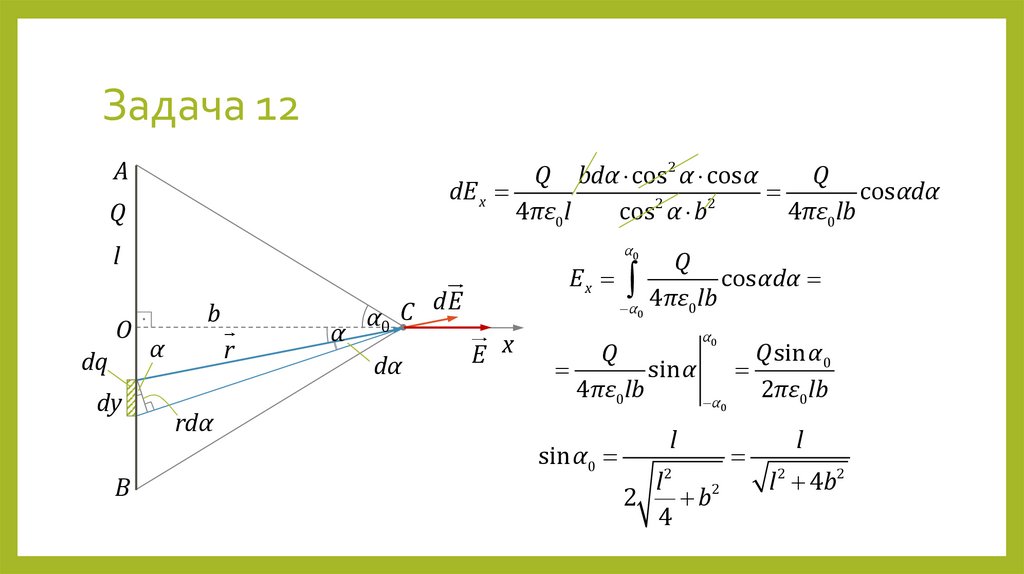
24. Задача 12

Тонкий стержень длиной l равномерно заряжен зарядом Q. Найти
напряжённость электрического поля в точке, лежащей на перпендикуляре к
стержню, проведённом через его середину, на расстоянии b от стержня.
РЕШЕНИЕ
dq r
Поле точечного заряда dE
4πε0 r 3
E E x dE x dE cos α dq cos α
4πε0r 2
b
dq τdy
r
cos α
Принцип суперпозиции E dE
Q
τ
l
rdα
bdα
dy
cos α cos2 α

25. Задача 12

A
Q bdα cos2 α cos α
Q
dE x
cos αdα
2
2
4πε0l
cos α b
4πε0lb
Q
l
O
dq
dy
B
α0
b
·
α
r
rdα
α
dE
C
α0
dα
Q
Ex
cos αdα
4πε0lb
α0
E x
α0
Q sin α0
Q
sin α
4πε0lb
2πε0lb
α
0
sin α0
l
l2
2
b2
4
l
l 2 4b2

26. Задача 12

E
Предельные случаи
Q
2πε0b l 2 4b2
Q
Q
1) b >> l: E
— поле точечного заряда
2
2πε0b 2b 4πε0b
Q
τ
2) b << l : E
— поле длинной нити
2πε0bl 2πε0b

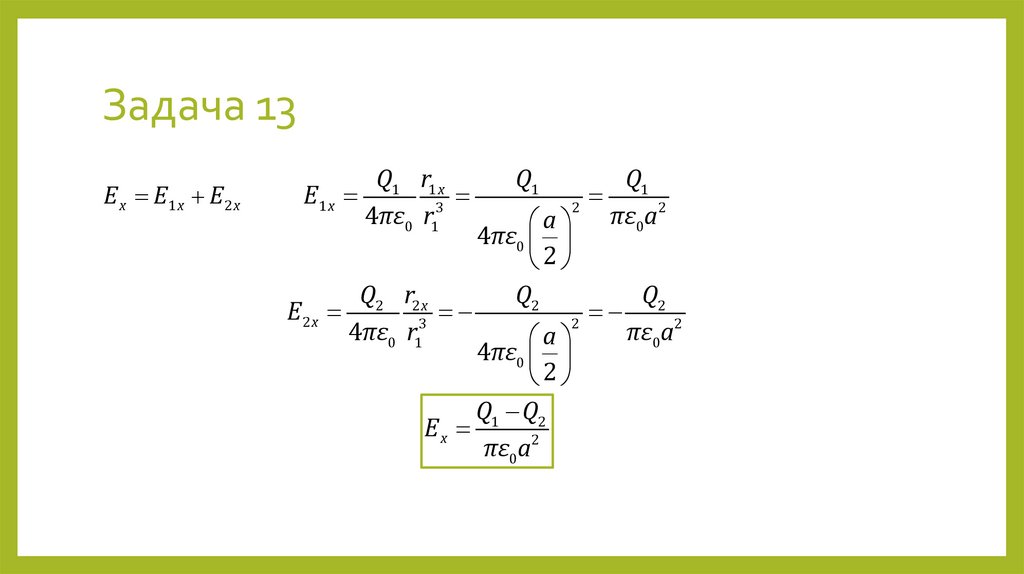
27. Задача 13

Два точечных заряда Q1 и Q2 расположены на расстоянии a друг от друга.
Найти напряжённость и потенциал электростатического поля в середине
отрезка, соединяющего заряды. Принять потенциал равным нулю в
бесконечно удалённой точке.
РЕШЕНИЕ
Q1⊕
r1
E2
a/2
O
r2
⊕ Q2
E1
a/2
x
Q1 r1
Q2 r2
Поле точечного заряда E1
E2
3
4πε0 r1
4πε0 r23
Принцип суперпозиции E E1 E2

28. Задача 13

E x E1 x E 2 x
Q1 r1 x
E1 x
3
4πε0 r1
Q1
Q1
2
2
πε
a
a
0
4πε0
2
Q2 r2 x
Q2
Q2
E2 x
2
3
2
4πε0 r1
πε
a
a
0
4πε0
2
Q1 Q2
Ex
πε0a2

29. Задача 13

Q1
Q1
Q1
Потенциал поля точечного заряда φ1
4πε0r1 4πε a 2πε0a
0
2
Принцип суперпозиции φ φ1 φ2
Q1 Q2
φ
2πε0a
Q2
φ2
2πε0a

30. Задача 15

Тонкий стержень длиной l равномерно заряжен с линейной плотностью τ. На
продолжении стержня на расстоянии a от его ближнего конца расположен
точечный заряд q. Найти силу, с которой поле стержня действует на заряд.
РЕШЕНИЕ
B τ, l
A
a
q
⊕
E
F
τl
Напряжённость поля стержня (см. задачу 9) E
4πε0a a l
qτl
F
F qE
4πε0a a l

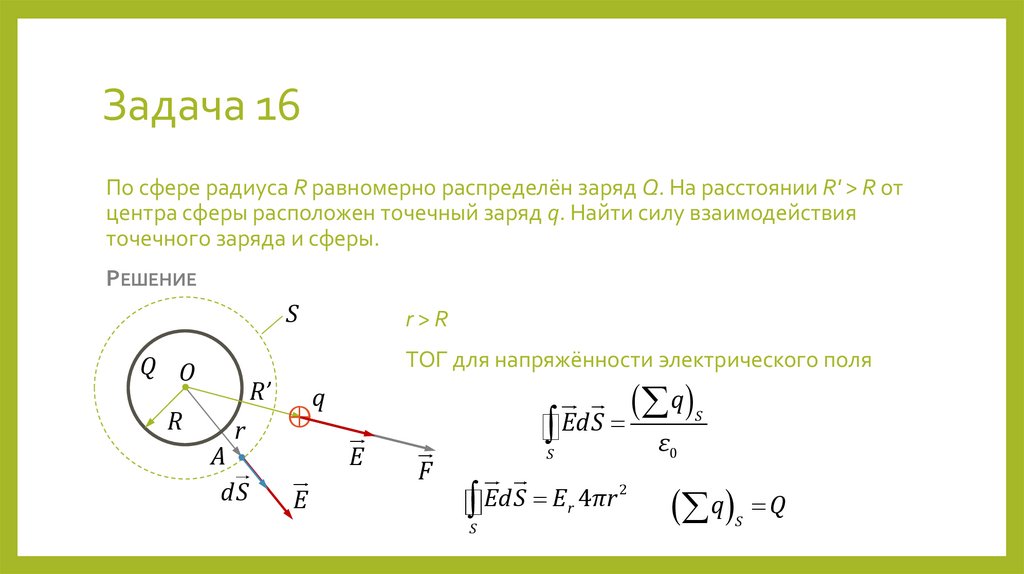
31. Задача 16

По сфере радиуса R равномерно распределён заряд Q. На расстоянии R' > R от
центра сферы расположен точечный заряд q. Найти силу взаимодействия
точечного заряда и сферы.
РЕШЕНИЕ
S
ТОГ для напряжённости электрического поля
Q O
R
r>R
R’
r
A
dS
q
⊕
E
E
F
q
EdS
S
2
EdS
E
4
πr
r
S
S
ε0
q
S
Q

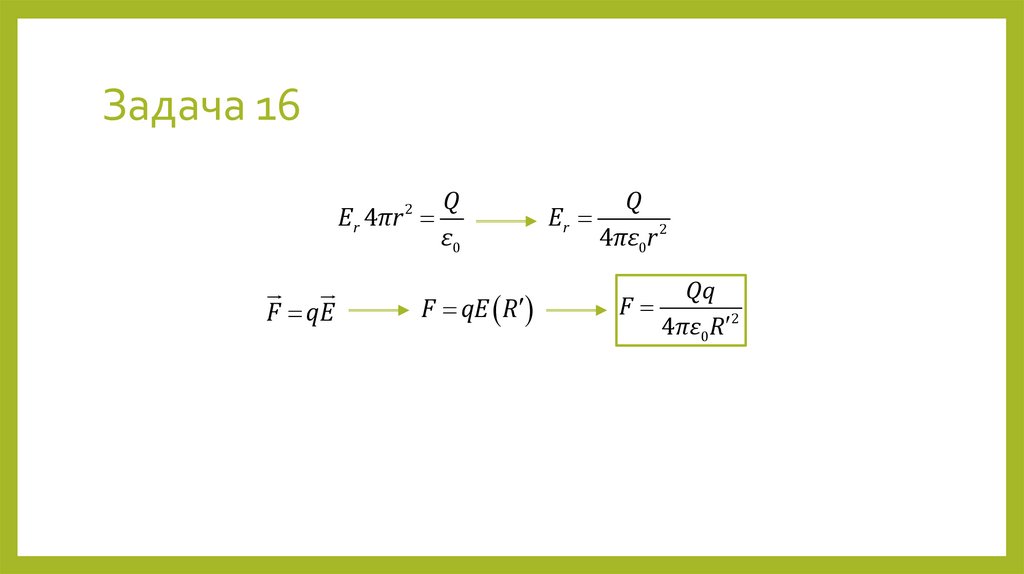
32. Задача 16

Q
E r 4πr
ε0
2
F qE
F qE R
Q
Er
4πε0r 2
F
Qq
4πε0R 2

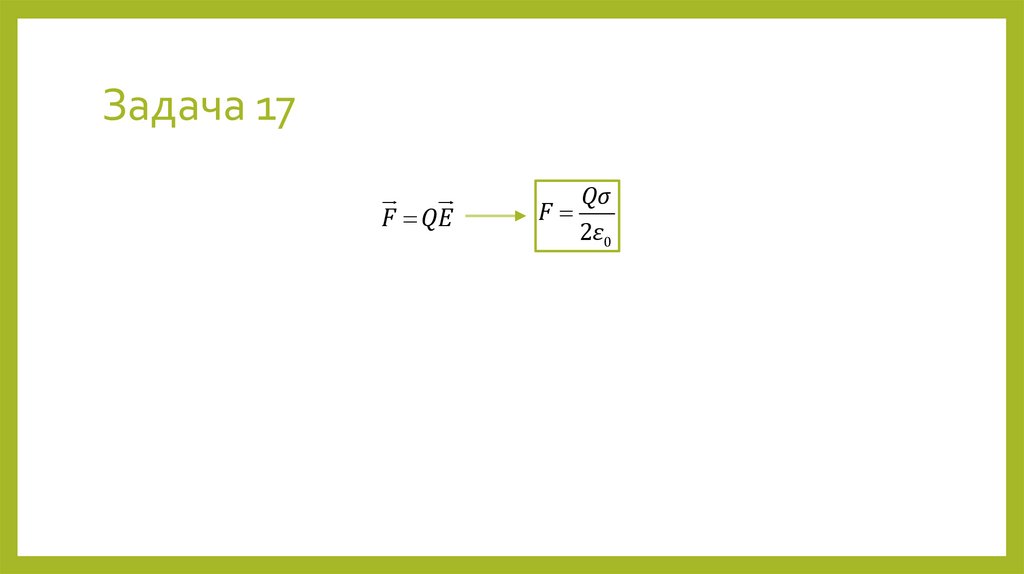
33. Задача 17

Имеется плоскость, равномерно заряженная с поверхностной плотностью σ. На
расстоянии a от плоскости расположен точечный заряд Q. Найти силу
взаимодействия заряда и плоскости.
РЕШЕНИЕ
dS бок
σ
E
dS торц
C
B
σ
E
A dS торц
E
2x
0
a
S
x
Q
⊕
F
E

34. Задача 17

ТОГ для напряжённости электрического поля
q
EdS
S
EdS EdS
S
Sбок
бок
2
S торц
dS торц 2ES торц
S торц
q
2ES торц
ε0
π
E x dS бок cos 2 E x dS торц x cos0
2 Sторц
Sбок
EdS торц
2E
S
S
σS торц
ε0
σS торц
σ
E
2ε0

35. Задача 17

F QE
F
Qσ
2ε0

36. Задача 18

Длинный цилиндр радиуса R из диэлектрика проницаемостью ε заряжен
равномерно по объёму с плотностью ρ. Найти Dr(r), где r — расстояние от оси
цилиндра, и построить соответствующий график.
РЕШЕНИЕ
I
h
ρ B dS IIбок DII
dS Iбок
II r
A
DI
R
ε
SI
SII
I. r > R
ТОГ для электрического смещения
DdS q
I
SI
DdS
I
DIr 2πrh
SI
DIr 2πrh πρR 2h
2
q
ρ
πR
h
S
I
ρR 2
DIr
2r
SI

37. Задача 18

II. r < R
DdS q
II
S II
DdS
S II
II
DIIr 2πrh
q
Dr
ρR
2
0
S II
ρ πr 2h
S II
DIIr 2πrh πρr 2h
II
I
R
r
DIIr
ρr
2

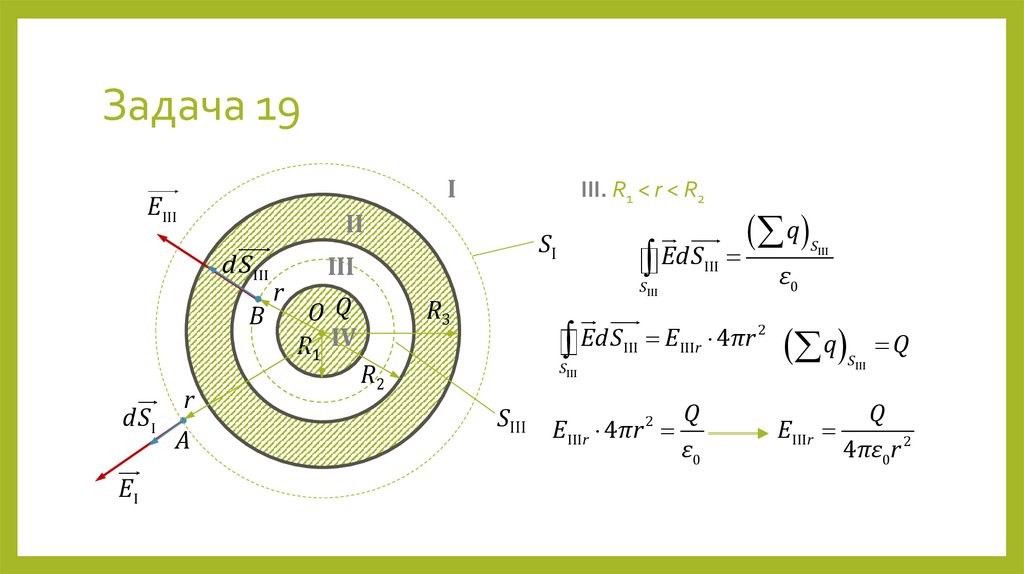
38. Задача 19

Металлический шар радиуса R1 окружён концентричной ему металлической
сферической оболочкой, внутренний радиус которой R2 = 2R1, а внешний
R3 = 3R1. Заряд шара равен Q, оболочка не заряжена. Найти потенциал шара и
построить график φ(r), где r — расстояние от центра шара. Принять потенциал
равным нулю в бесконечно удалённой точке.
РЕШЕНИЕ
I. r > R3
ТОГ для напряжённости электрического поля: EdS I
SI
2
EdS
E
4
πr
I Ir
SI
q
SI
Q
Q
E Ir 4πr
ε0
2
q
SI
ε0
Q
E Ir
4πε0r 2

39. Задача 19

I
E III
II
dS III
B
dS I
EI
III. R1 < r < R2
r
A
r
SI
III
O Q
R1 IV
EdSIII
q
S III
R3
2
EdS
E
4
πr
III IIIr
R2
S III
SIII
Q
E IIIr 4πr
ε0
2
S III
ε0
q
E IIIr
S III
Q
Q
4πε0r 2

40. Задача 19

II. R2 < r < R3
IV. r < R1
Поле в металле E IIr E IVr 0
Интегральная связь напряжённости и потенциала электростатического поля:
r
φ r E r dr
r
r
r
Q
Q 1
Q
I. φ r E Ir dr
dr
2
4πε0r
4πε0 r 4πε0r
Q
φ r
4πε0r

41. Задача 19

R3
R3
r
r
Q
Q
dr 0dr
II. φ r E Ir dr E IIr dr
2
4πε0r
4πε0R3
R3
R3
R3
R2
R3
r
R2
Q
φ r
12πε0R1
r
Q
Q
III. φ r E Ir dr E IIr dr E IIIr dr
R
R
4πε0r 2 dr R 0dr R 4πε0r 2 dr
3
2
3
2
r
Q
Q 1
Q
Q 1 1
4πε0R3 4πε0 r R2 4πε0R3 4πε0 r R2
Q 1 1
1
Q 1 1
Q 1 1
φ r
φ r
4πε0 r 2R1 3R1 4πε0 r 6R1
4πε0 r 6R1

42. Задача 19

R3
R2
R1
r
R3
R2
R1
φ r E Ir dr E IIr dr E IIIr dr E IVr dr
IV.
R3
R2
R1
Q
Q
Q 1 1 1
dr 0dr
dr 0dr
2
2
4πε0r
4πε0r
4πε0 R1 R2 R3
R3
R2
R1
r
Q 1
1
1
Q 6 3 2
5Q
φ r
4πε0 R1 2R1 3R1 4πε0 6R1
24πε0R1
5Q
φ r
24πε0R1

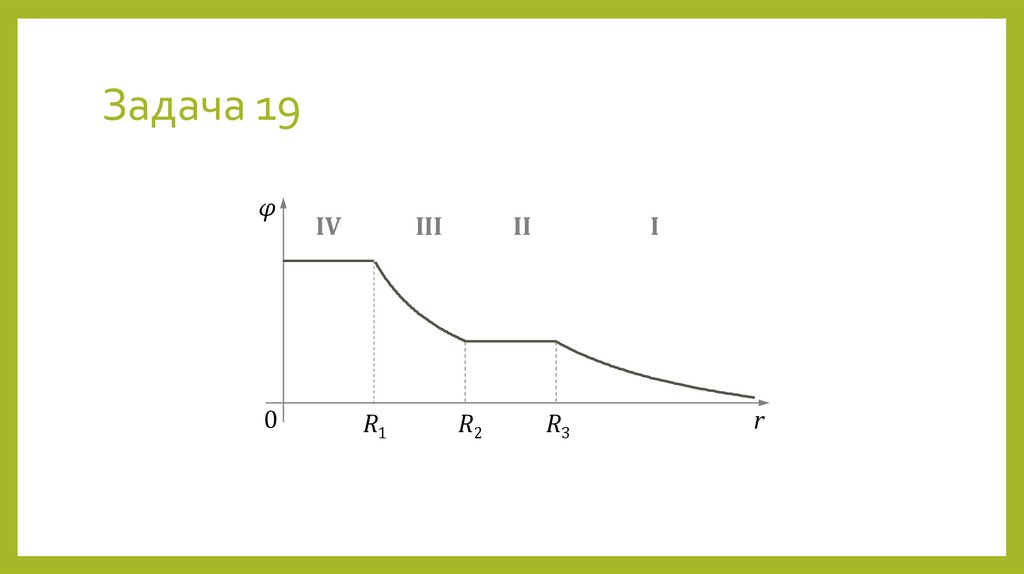
43. Задача 19

φ
0
IV
III
R1
II
R2
I
R3
r

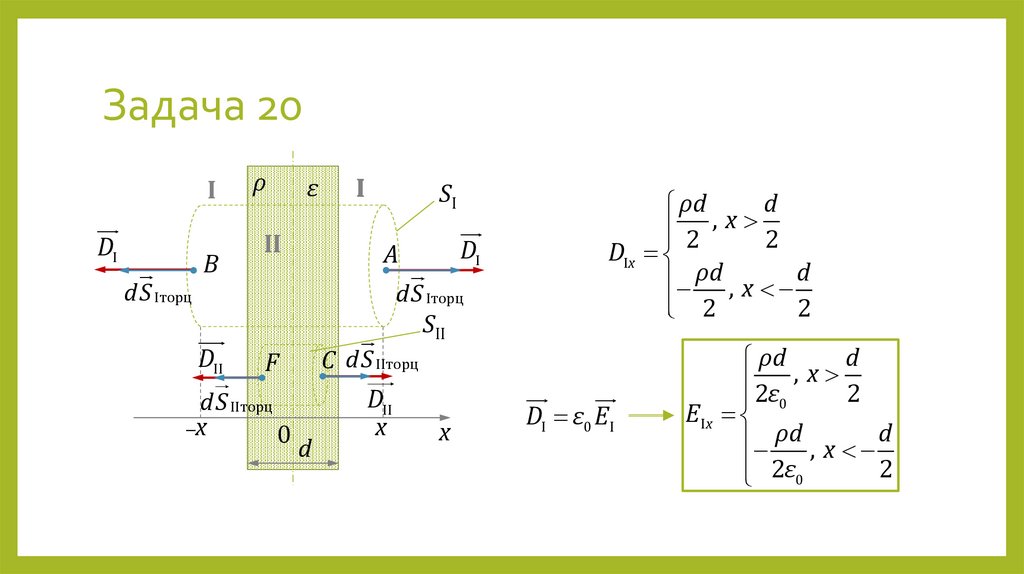
44. Задача 20

Плоский слой толщиной d из диэлектрика проницаемостью ε заряжен
равномерно по объёму с плотностью ρ. Найти Ex(x), где ось x направлена
перпендикулярно слою, и построить соответствующий график. Координата x
отсчитывается от середины слоя.
РЕШЕНИЕ
I. |x| > d/2
ТОГ для электрического смещения:
DdS q
I
SI
DdS
SI
I
2DI S Iторц
q
SI
ρd S Iторц
SI
2DI S Iторц ρd S Iторц
DI
ρd
2

45. Задача 20

I
DI
dS Iторц
B
DII
ρ
ε
II
I
SI
DI
A
dS Iторц
SII
C dS IIторц
F
dS IIторц
–x
0
d
ρd
2 , x 2
DIx
ρd , x d
2
2
d
DII
x
x
DI ε0 E I
d
ρd
2ε , x 2
0
E Ix
ρd , x d
2ε0
2

46. Задача 20

II. |x| < d/2
DdS q
II
S II
DdS
II
S II
q
2DII S IIторц
S II
2DII S IIторц ρ 2 x S IIторц
ρ 2 x S IIторц
DIIx ρx
DII ρ x
DII ε0εE II
S II
E IIx
ρx
ε0ε

47. Задача 20

Ex
I
II
I
‒d/2
0 d/2
x

48. Задача 21

Воздушный конденсатор ёмкостью C заряжают от источника, напряжение на
клеммах которого равно U, а затем отключают от источника. После этого
конденсатор заполняют жидким диэлектриком проницаемостью ε. Какую
работу при этом совершают внешние силы? Ответить на вопрос задачи в
случае, когда конденсатор подключён к источнику.
РЕШЕНИЕ
ε
C → С’
К
E=U
Ёмкость конденсатора после заполнения диэлектриком
C εC

49. Задача 21

А) Ключ К разомкнут.
Заряд конденсатора q q const q CU
Закон сохранения энергии: ΔW A*
A* — работа внешних сил, ΔW — изменение энергии конденсатора
2 2
2
q2 q2 C 2U 2 1 1 C U C εC CU 1 ε
ΔW W W
2C 2C
2 C C
2C εC
2ε
2
CU
1 ε
*
A
A* 0
2ε

50. Задача 21

Б) Ключ К замкнут.
Напряжение на обкладках конденсатора U U const
Закон сохранения энергии: ΔW A* Aист
Aист — работа источника
CU 2 ε 1
C U 2 CU 2 U 2
ΔW W W
C C
2
2
2
2
Aист EΔq U q q U C U CU U 2 C C CU 2 ε 1
A* ΔW Aист
CU 2 ε 1
2
CU 2 ε 1
CU 2 ε 1
2

51. Задача 21

2
CU
ε 1 A* 0
*
A
2

52. Задача 22

Шар радиуса R из диэлектрика проницаемостью ε заряжен равномерно по
объёму с плотностью ρ. Найти энергию электрического поля, заключённую
внутри шара.
РЕШЕНИЕ
r<R
D
dS
B
r
ρ
ТОГ для электрического смещения
S
ε
O
R
DdS q
S
2
DdS
D
4
πr
r
S
4
Dr 4πr πρr 3
3
2
q
S
4 3
ρ πr
3
ρr
Dr
3
S

53. Задача 22

D ε0εE
Dr
ρr
Er
ε0ε 3ε0ε
Объёмная плотность энергии электрического поля
DE Dr E r 1 ρr ρr
ρ2r 2
w
2
2
2 3 3ε0ε 18ε0ε
ρ
O
dV
R
Разобьём шар на тонкие сферические слои объёмом
r
dr
dV 4πr 2dr

54. Задача 22

Энергия электрического поля в объёме dV
2 4
ρ2r 2
2
πρ
r dr
2
dW wdV
4πr dr
18ε0ε
9ε0ε
R
2πρ2 4
2πρ2 R5 2πρ2R 4
W
r dr
9ε0ε
9ε0ε 5
45ε0ε
0
2πρ2R 4
W
45ε0ε

55. Задача 23

Имеются две большие параллельные металлические пластины площадью S,
заряды которых равны Q1 и Q2. Найти силу взаимодействия пластин.
РЕШЕНИЕ
S
S
Q1
Q2
σ1
Q1
E1
(см. задачу 17)
2ε0 2ε0 S
F12
E1
F12 Q2 E1
F12
Q1Q2
2ε0 S

56. Задача 25

Два заряженных конденсатора соединили параллельно одноимённо
заряженными обкладками. Заряд одного конденсатора равен q1, его ёмкость —
C1, другого конденсатора — соответственно q2 и C2. Чему равна разность
потенциалов на конденсаторах после их соединения?
РЕШЕНИЕ
q q1 q2
C1
–
+
C2
C C1 C 2
q q1 q2
U
C C1 C 2
q1 q2
U
C1 C 2