Внецентренное приложение нагрузки. Ядро сечения

1.

Практическое занятие:
Внецентренное приложение нагрузки.
Ядро сечения.
Задача 5.2

2.

Условие задачи: Короткий стержень сжимается силой F, проходящей через
заданную точку и направленной параллельно продольной оси стержня.
Исходные данные: точка приложения силы F – точка В; расчётное
сопротивление на растяжение материала Rt =0,25 МПа; расчётное
сопротивление на сжатие материала Rc=2,5 МПа.
Требуется:
1. Построить нейтральную ось.
2. Из условия прочности определить величину допускаемой силы [F].
3. При силе равной [F], вычислить нормальные напряжения в точках
сечения, наиболее удалённых от нейтральной оси в зонах растяжения и
сжатия. Построить эпюру нормальных напряжений в поперечном
сечении стержня.
4. Построить ядро сечения.

3.

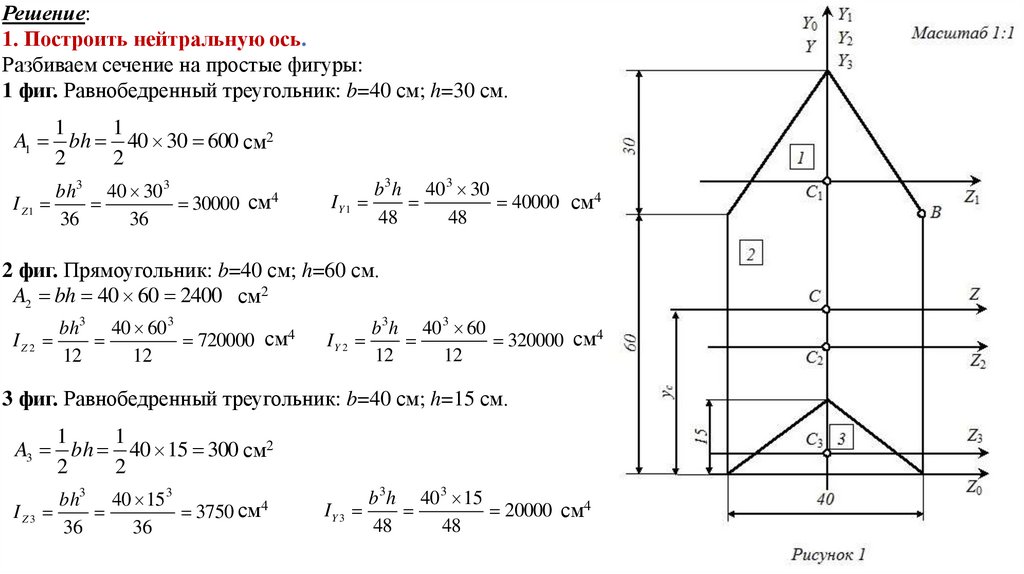
Решение:
1. Построить нейтральную ось.
Разбиваем сечение на простые фигуры:
1 фиг. Равнобедренный треугольник: b=40 см; h=30 см.
1
1
A1 bh 40 30 600 см2
2
2
bh3 40 30 3
I Z1
30000 см4
36
36
b 3 h 40 3 30
IY1
40000 см4
48
48
2 фиг. Прямоугольник: b=40 см; h=60 см.
A2 bh 40 60 2400 см2
IZ2
bh3 40 60 3
720000 см4
12
12
IY 2
b 3 h 40 3 60
320000 см4
12
12
3 фиг. Равнобедренный треугольник: b=40 см; h=15 см.
1
1
A3 bh 40 15 300 см2
2
2
IZ3
bh3 40 15 3
3750 см4
36
36
IY 3
b 3 h 40 3 15
20000 см4
48
48

4.

Относительно вспомогательных осей Y0 и Z0 определяем координаты всего центра тяжести:
S Z(i0) S Z(10) S Z( 20) S Z(30) y1 A1 y 2 A2 y3 A3
, здесь
yC
A
A1 A2 A3
A1 A2 A3
y1 – это расстояние между осями Z0 и Z1. y1=70 см.
y2 – это расстояние между осями Z0 и Z2. y2=30 см.
y3 – это расстояние между осями Z0 и Z3. y3=5 см.
yC
70 600 30 2400 5 300
41,67 см
600 2400 300
SY(i0) SY(10) SY( 20) SY(30) z1 A1 z 2 A2 z3 A3 , здесь
zC
A
A1 A2 A3
A1 A2 A3
z1 – это расстояние между осями Y0 и Y1. z1=0 см.
z2 – это расстояние между осями Y0 и Y2. z2=0 см.
z3 – это расстояние между осями Y0 и Y3. z3=0 см.
zC
0 600 0 2400 0 300
0
600 2400 300

5.

Относительно вспомогательных осей Y0 и Z0 откладываем центр тяжести всего сечения точку С(yc; zc).
Через точку С(41,67; 0) проводим центральные оси Y и Z.
Так как ось Y является ось симметрии всего сечения, поэтому оси Y и Z являются главными центральными
осями всего сечения.
Определяем главные центральные моменты инерции всего сечения:
I Z I Z(i ) I Z(1) I Z( 2) I Z(3) I Z 1 a12 A1 I Z 2 a22 A2 I Z 3 a32 A3 , здесь
a1 – это расстояние между осями Z и Z1.
a1=y1–yc= 70 – 41,67 = 28,33 см.
a2 – это расстояние между осями Z и Z2.
a2=y2–yc= 30 – 41,67 = -11,67 см.
a3 – это расстояние между осями Z и Z3.
a3=y3–yc= 5 – 41,67 = -36,67 см.
I
2
2
I Z 30000 28,332 600 720000 11,67 2400 3750 36,67 300 113,135 10 4 см4
I Y I Y(i ) I Y(1) I Y( 2) I Y(3)
2
2
2
b
A
I
b
A
I
b
Y1
1
1
Y2
2
2
Y3
3 A3 , здесь
b1 – это расстояние между осями Y и Y1.
b1=z1–zc= 0 – 0 = 0 см.
b2 – это расстояние между осями Y и Y2.
b2=z2–zc= 0 – 0 = 0 см.
b3 – это расстояние между осями Y и Y3.
b3=z3–zc= 0 – 0 = 0 см.
I Y 40000 02 600 320000 02 2400 20000 02 300 34 10 4 см4

6.

Определяем квадраты главных центральных радиусов инерции всего сечения:
IY
IY
34 10 4
iY
126 см2
A
A1 A2 A3 600 2400 300
2
IZ
IZ
113,135 10 4
iZ
419 см2
A
A1 A2 A3 600 2400 300
2
Определяем отрезки, отсекаемые нулевой линией на координатных осях:
iZ2
aY
yF
iY2
, здесь
aZ
zF
yF и zF – координаты точки приложения внешней силы F. Внешняя сила приложена в точке В, которая имеет
координаты относительно осей Z и Y: yF = yB = 18,33 см
zF = zB = 20 см
126
419
aZ
6,3 см
aY
22,9 см
20
18,3
На расчётной схеме на координатных осях Y и Z откладываем отрезки ay и az. И через две точки проводим
нулевую линию.
2. Из условия прочности определить величину допускаемой силы [F].
Определяем положение опасных точек. Опасные точки – это точки наиболее удалённые от нейтральной линии
и в этих точках нормальные напряжения принимают экстремальное значение.

7.

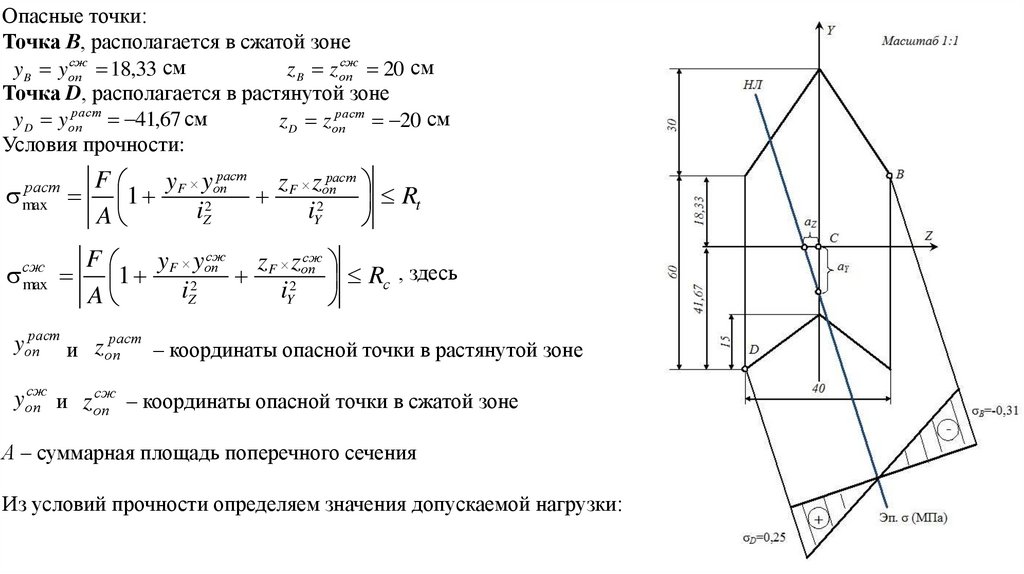
Опасные точки:
Точка В, располагается в сжатой зоне
сж
сж
z B zоп
20 см
yB yоп
18,33 см
Точка D, располагается в растянутой зоне
раст
раст
y D yоп
41,67 см
z D zоп
20 см
Условия прочности:
раст
max
сж
max
F
yF yопраст z F zопраст
1
Rt
2
2
i
i
A
Z
Y
F
yF yопсж z F zопсж
1
Rс , здесь
2
2
iZ
iY
A
раст
раст
yоп
и z оп
– координаты опасной точки в растянутой зоне
сж
сж
yоп
и z оп
– координаты опасной точки в сжатой зоне
А – суммарная площадь поперечного сечения
Из условий прочности определяем значения допускаемой нагрузки:

8.

F
раст
A Rt
yF yопраст z F zопраст
1
iZ2
iY2
2700 10 4 0,25 10 3
16,92 кН
18,33 41,67 20 20
1
419
126
A Rc
2700 10 4 2,5 103
F
135,54 кН
сж
сж
y y
18,33 18,33 20 20
z z
1
1 F 2 оп F 2 оп
iZ
iY
419
126
Из двух найденных значений сил выбираем минимальное. Принимаем [F]=16,92 кН.
сж
3. При силе равной [F], вычислить нормальные напряжения в точках сечения, наиболее удалённых от
нейтральной оси в зонах растяжения и сжатия. Построить эпюру нормальных напряжений в
поперечном сечении стержня.
Определяем напряжения в опасных точках:
F
yF y A z F z A 16,92 103 18,33 41,67 20 20
D 1
2
1
0,25 МПа
2
4
i
i
419
126
A
Z
Y
2700 10
F
yF yB zF zB 16,92 103 18,33 18,33 20 20
B 1 2 2
1
0,31 МПа
4
i
i
419
126
A
Z
Y
2700 10
Знак силы F подставляется по смыслу, так как сила сжимающая, то её значение отрицательное.
На расчётной схеме через опасные точки проводим касательные параллельные нулевой линии и строим эпюру
нормальных напряжений.

9.

4. Построить ядро сечения
Для построения ядра сечения, необходимо по всему контуру
поперечного сечения провести касательные, которыми являются
нулевые линии. При проведении касательных внутренние углы
надо обходить.
Для определения координат ядровых точек воспользуемся
соотношениями:
(i )
y Fя
iZ2
(i )
ay
(i )
z Fя
iY2
(i ) , здесь
az
(i )
a (iy ) и a z – отрезки, которые нулевая линия отсекает на
координатных осях
iY2 126 см2 iZ2 419 см2 – квадраты радиусов инерции
поперечного сечения
Нулевая линия 1-1
a(y1) 48,33 см
(1)
y Fя
az(1) 32,22 см
419
8,67 см
48,33
(1)
z Fя
126
3,91 см
32,22

10.

Нулевая линия 2-2
a(y2) 48,33 см
az( 2) 32,22 см
( 2)
y Fя
419
8,67 см
48,33
( 2)
z Fя
126
3,91 см
32,22
Нулевая линия 3-3
a (y3)
az(3)
20 см
(3)
y Fя
419
0 см
( 2)
z Fя
126
6,3 см
20
Нулевая линия 4-4
a(y4)
41,67 см
az( 4)
( 4)
y Fя
419
10,06 см
41,67
( 4)
z Fя
126
0 см
Нулевая линия 5-5
a (y5)
az(5)
20 см
( 5)
y Fя
419
0 см
( 5)
z Fя
126
6,3 см
20
Координаты ядровых точек откладываем в масштабе относительно центральных осей Y и Z. Ядровые точки
соединяем прямыми линиями и получаем ядро сечения.