Похожие презентации:
Геометрические характеристики сечений
1. Геометрические характеристики сечений
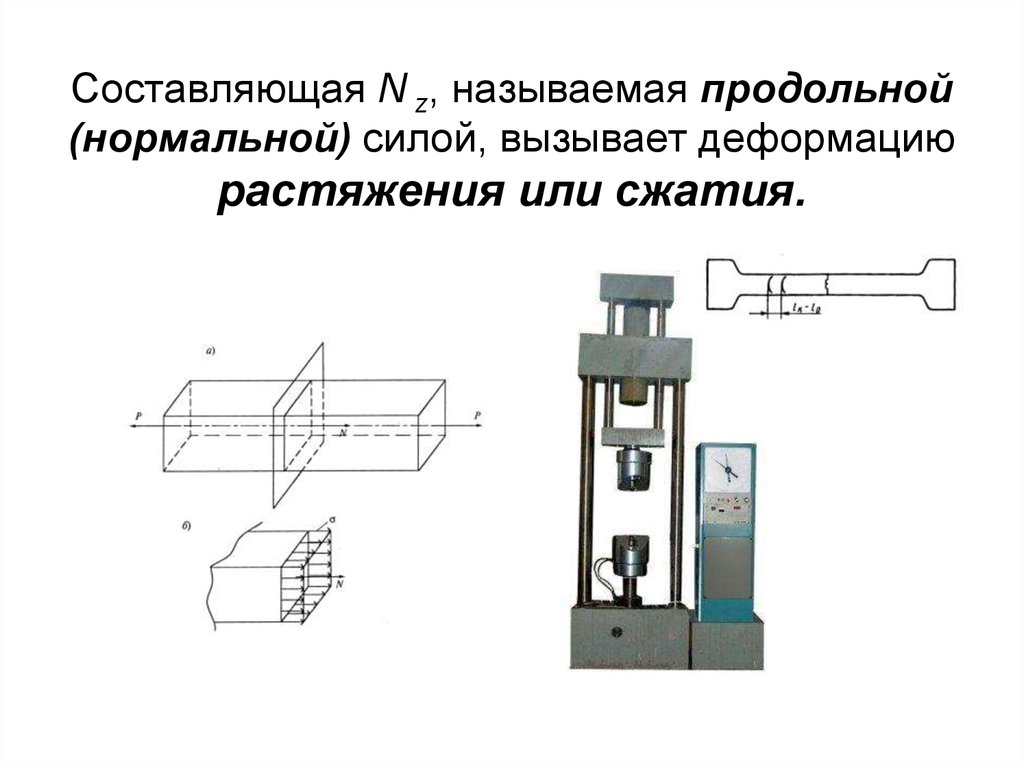
2. Составляющая N z, называемая продольной (нормальной) силой, вызывает деформацию растяжения или сжатия.
3.
• При деформации растяжения сжатияплощадь поперечного сечений полностью
характеризовала прочность и жесткость
детали.
N
A
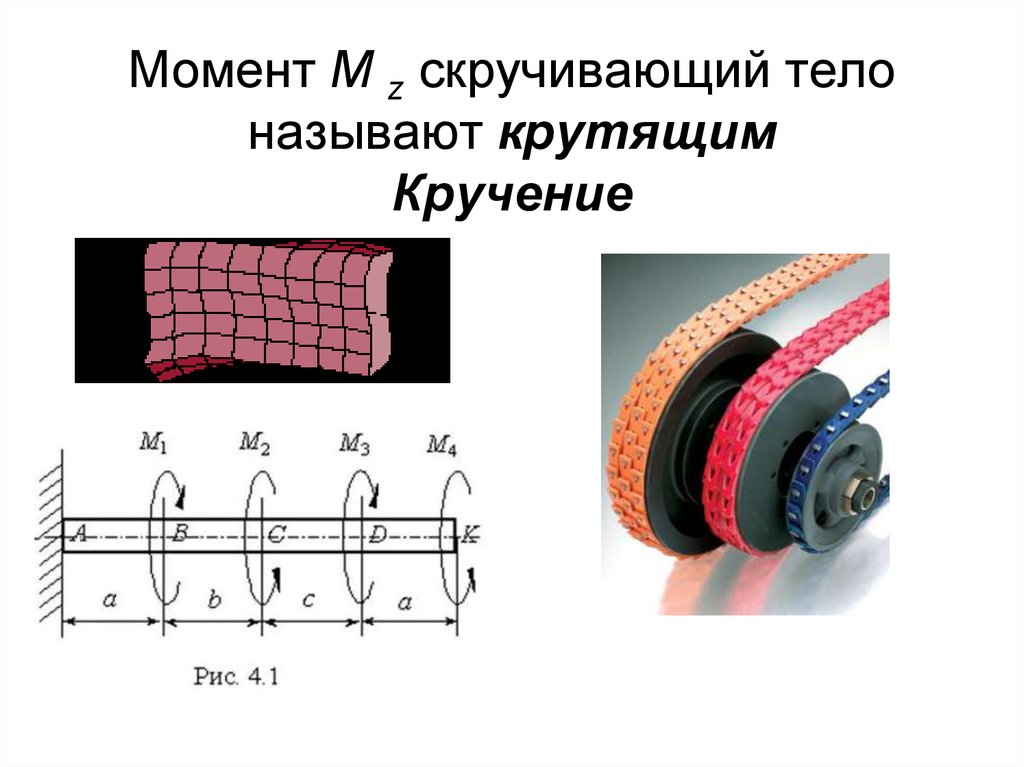
4. Момент M z скручивающий тело называют крутящим Кручение
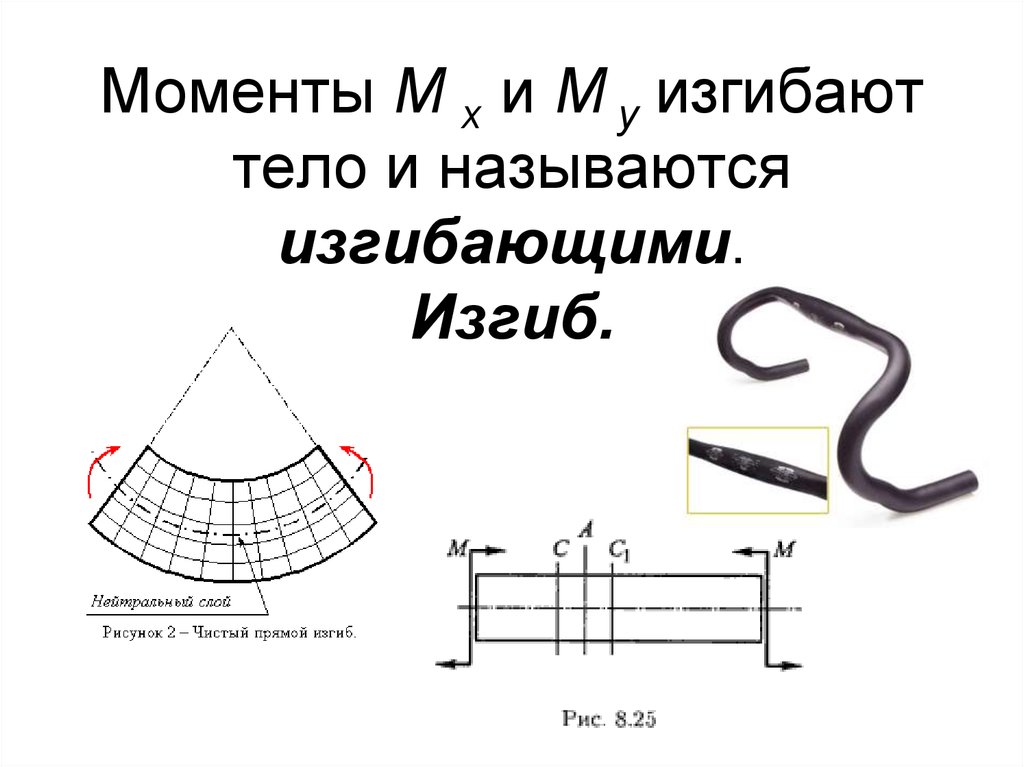
5. Моменты M x и M y изгибают тело и называются изгибающими. Изгиб.
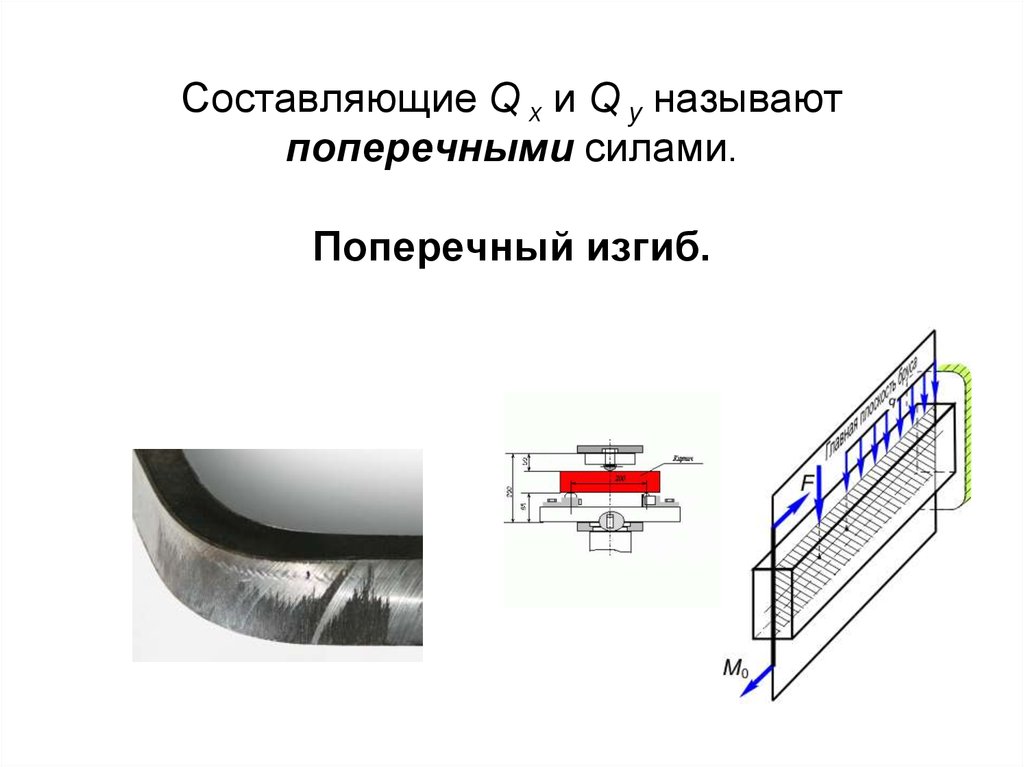
6. Составляющие Q x и Q y называют поперечными силами. Поперечный изгиб.
7.
• Однако при деформации изгиба икручения прочность и жесткость
характеризуются не только размерами
сечения, но и его формой. К числу
геометрических характеристик сечения,
учитывающих оба указанных фактора,
относятся статические моменты,
моменты инерции, моменты,
сопротивления.
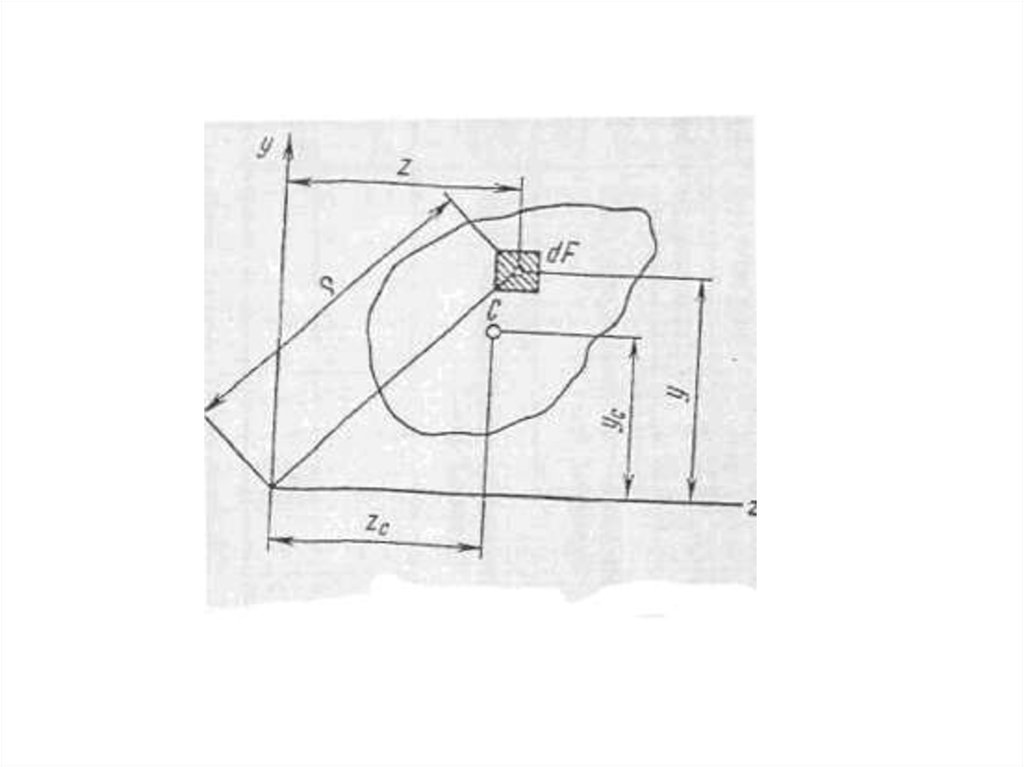
8. Статические моменты площадей
• Координаты zc и ус центра тяжестиплоской фигуры определяются, как
известно из общей механики
формулами.
• где F -площадь всей фигуры; dF элемент площади.
9.
10.
• Статический момент площади фигурыотносительно какой-либо оси равен
сумме статических моментов частей, из
которых состоит фигура, относительно
той же оси.
• Оси, проходящие через центр тяжести
фигуры, называют центральными
осями. Статические моменты площадей
относительно центральных осей равны
нулю, так как zc = 0 или ус = 0.
11.
• Различают осевые, полярные ицентробежные моменты инерции.
• Осевым моментом инерции сечения
называют взятую по всей площади
сечения сумму произведений
элементарных площадок на квадраты
их расстояний до соответствующей оси.
Обозначая моменты у инерции
относительно осей z и y соответственно
через J z и J y
12.
13.
• Полярным моментом инерции (моментоминерции относительно полюса) называют
взятую по всей площади сечения сумму
произведений элементарных площадок на
квадраты их расстояний до данного полюса
14.
• Центробежным моментом инерции сеченияназывают взятую по всей площади сечения
сумму произведений элементарных площадок на обе координаты в данной
прямоугольной системе осей. Обозначая
центробежный момент инерции через J zy
имеем
15.
• Из приведенных определений следует, чтомомент инерции сложной фигуры равен
сумме моментов инерции ее частей.
• Полярный момент инерции относительно
полюса, являющегося началом
прямоугольной системы координат, равен
сумме моментов инерции относительно осей
данной системы
16.
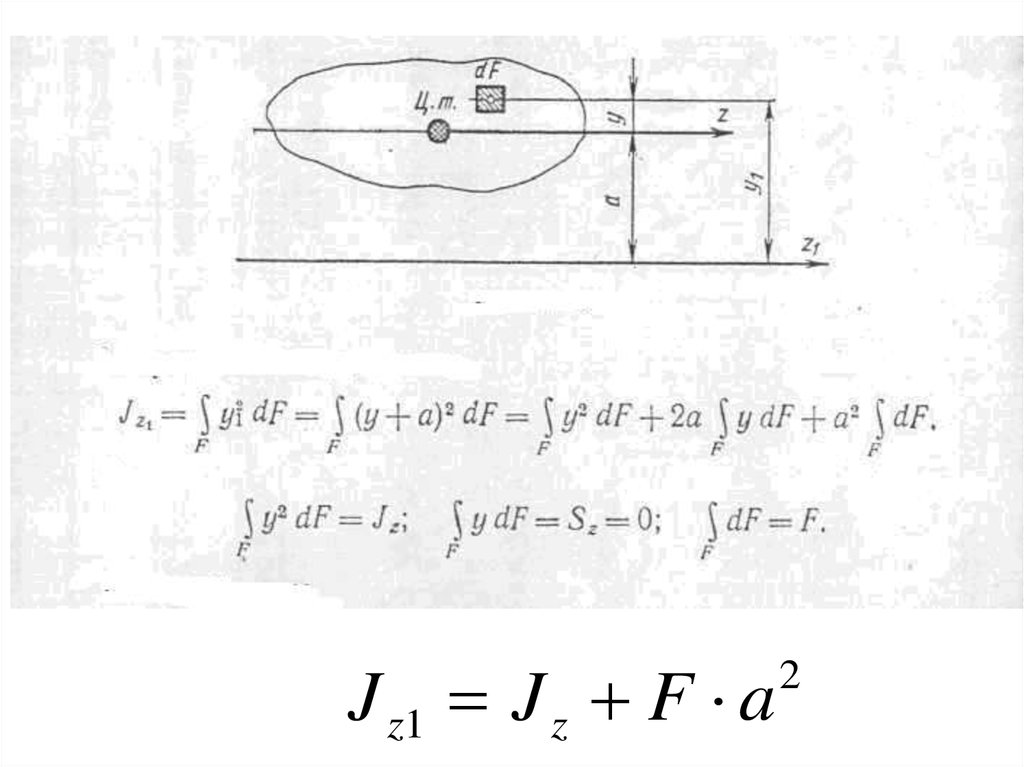
• Момент инерции сечения относительнокакой-либо оси равен моменту инерции этого
сечения относительно центральной оси,
параллельной данной, сложенному с
произведением площади сечения на квадрат
расстояния между осями
J z1 J z F a
2
17.
• Центробежным моментом инерциисечения называют взятую по всей
площади сечения сумму произведений
элементарных площадок на обе
координаты в данной прямоугольной
системе осей.
• Центробежный момент инерции J zy
18.
J z1 J z F a2
19.
• Две взаимно перпендикулярные оси с началом вданной точке, для которых центробежный момент
инерции плоской фигуры равен нулю, называют
главными осями инерции фигуры в этой точке.
• Глазные оси инерции в центре тяжести фигуры
называют главными центральными осями инерции.
• Если хотя бы одна из двух взаимно
перпендикулярных осей, проходящих через центр
тяжести сечения, является осью симметрии, то такие
оси являются главными центральными осями
инерции.
20.
• главные центральные оси инерциифигуры могут быть найдены, если
известны ее центробежный J zy и
осевые Jz и Jy моменты инерции
относительно произвольно
расположенных центральных осей z и у.
Для этого систему осей zу необходимо
повернуть на угол α, определяемый из
соотношения.
21.
• Моменты инерции относительно главныхцентральных осей инерции называют
главными моментами инерции: они обладают
тем свойством, что один из них имеет
максимальное, а другой минимальное
значение по сравнению с моментами инерции
относительно остальных центральных осей.
22.
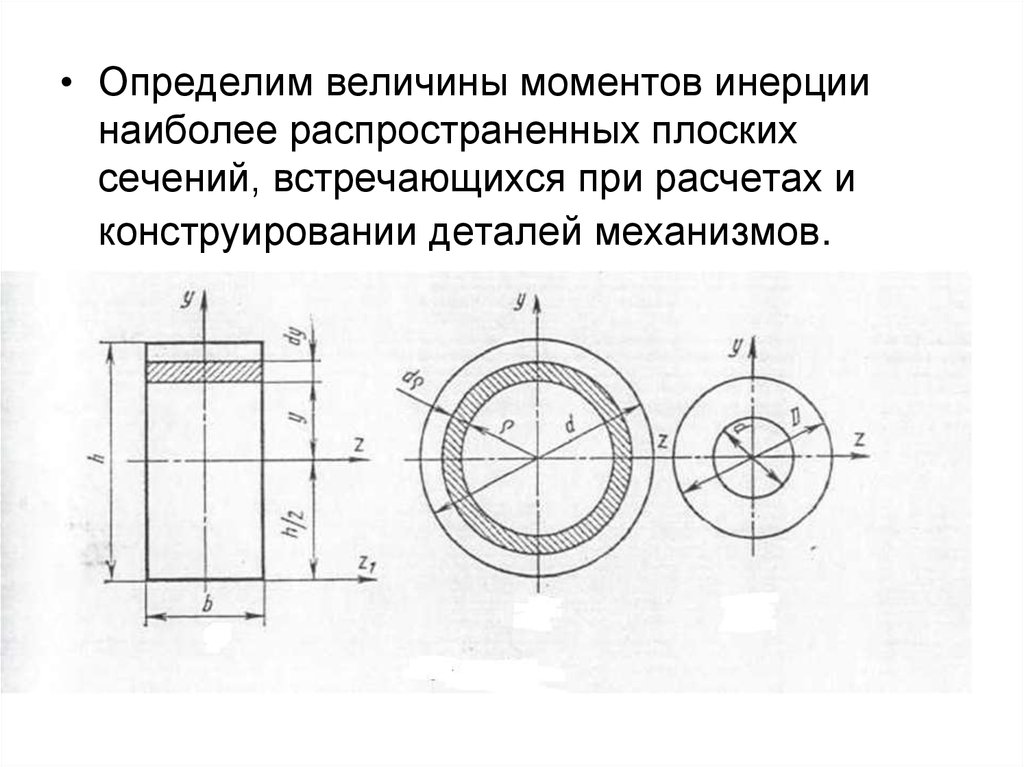
• Определим величины моментов инерциинаиболее распространенных плоских
сечений, встречающихся при расчетах и
конструировании деталей механизмов.
23.
• Прямоугольник высотой h и шириной b.Выделим в прямоугольнике элементарную
полоску высотой dy и шириной b. Полоска
отстоит от центральной оси г, параллельной
основанию на расстоянии у, gри этом у
изменяется в пределах
• от + h/ 2 до - h/2
24.
• Круговое кольцо с наружным диаметром D ивнутренним d.
• В данном случае полярный момент инерции
может быть получен как разность полярных
моментов инерции большого и малого круга
25.
• Обозначив d/D=C, после подстановкив выражение‘ получим из соотношения
• находим осевые моменты инерции
круга и кругового кольца
26.
• Для круга с учетом соотношения27. Для кольца
28.
29.
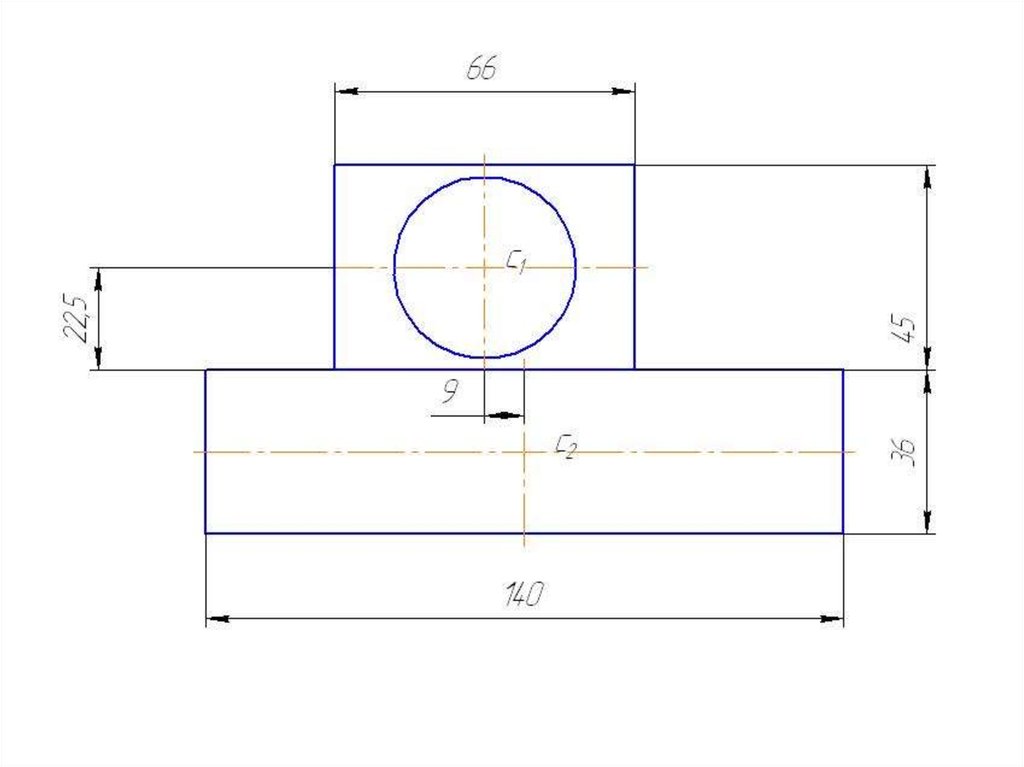
Даноh1 = 45 мм
b1 = 66 мм
h2 = 36 мм
b2= 140 мм
Отверстие d = 40 мм
Площади фигур
А 1 = h1* b1=45*66=2970 мм2
А 2 = h2* b2=36*140=5040 мм2
А 3 = πd2/4=3.14* 402 / 4 = 1256 мм2
30.
• Статические моменты инерцииотносительно выбранных осей
• Ось X
• S 1x= А 1 * y1 =2970*40.5=120285 мм3
• S 2x= А 2 * y2 =5040*0=0 мм3
• S 3x= А 3 * y3 =1256*40.5=50868 мм3
31.
Ось Y
S 1y= А 1 * x1 =2970*(-9)=26730 мм3
S 2y= А 2 * x2 =5040*0=0 мм3
S 3y= А 3 * x1 =1256*(-9)=11304 мм3
32. Построим главные оси системы:
33.
• Моменты инерции фигур относительнособственных осей:
• Ось X
34.
• Jxc = Jx1 +A1 *(y1 -yc )2 -Jx2 - A2 *(y2 -yc )2+Jx3 + A3 *(y3 -yc )2 =
• = 1078110+2670*(40.5-10.277)2 -125600
– 1256*(40.5 -10.277) 2 +8232000 +
• 5040*(0-10.277)2 = 11007151,55мм4
35.
• Ось Y36.
• Jyc = Jy1 +A1 *(x1 -xc )2 –Jy2 - A2 *(x2 -xc )2+Jy3 + A3 *(x3 -xc )2 =
• = 501187.5+2670*(9-4.1)2 -125600 –
1256*(9 -4.1) 2 +544320 +
• 5040*(0-4.1)2 = 1038580,04 мм4
• Центробежные момент инерции:
• Jxy1=A1 * (a1 -yc ) *(b1 -xc )=2670*(40.510.277)*(9-4.1)=395407,509 мм4
37.
• Jxy2=A2 * (a2 -yc ) *(b2 -xc )=1256*(40.510.277)*(9-4.1)=186004,4 мм4• Jxy3=A3 * (a3 -yc ) *(b3 -xc )=5040*(010.277)*(0-4.1)=212363,93 мм4
• Jxy = Jxy1 + Jxy 3- Jxy2
=395407,509+212363,93186004,4=793775,839мм4
38.
• Определим угол поворота39.
• α =4°31‘28''40.
• Определим моменты инерцииотносительно главных осей:
41.
42.
• Jmax = 11993195,12 мм4• Jmin = 52536,466 мм4






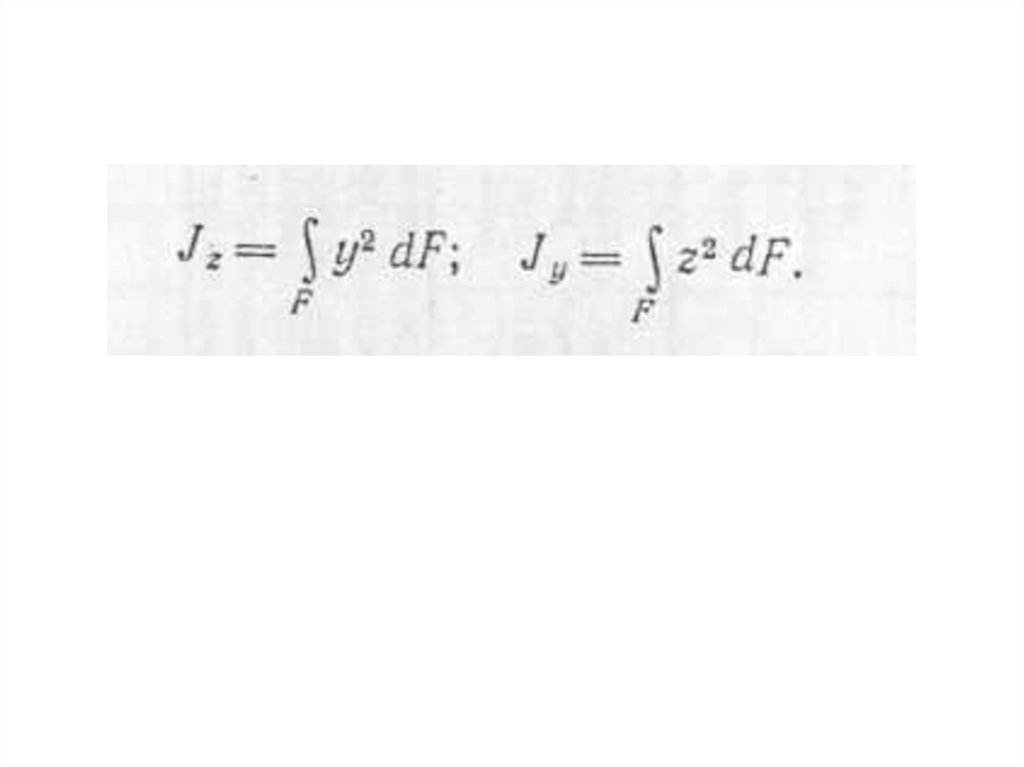















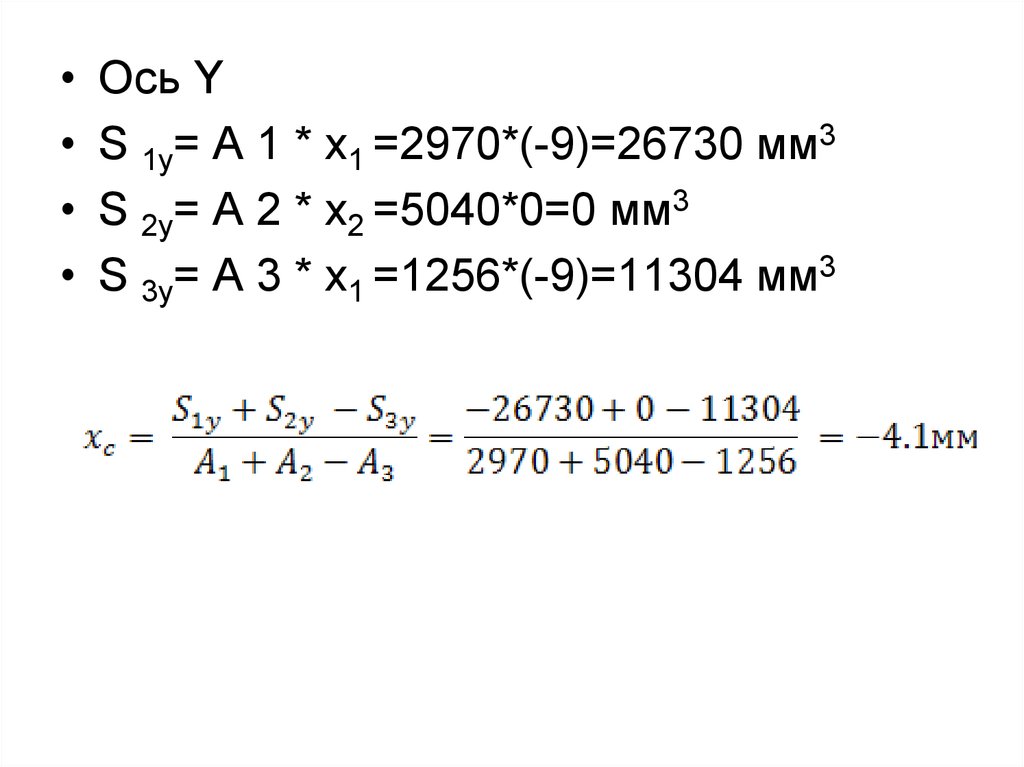











 Математика
Математика Физика
Физика








