Похожие презентации:
Начертательная геометрия. Лекция 2
1. Лекция 2
• Следы прямой линии• Взаимное положение прямых
• Теорема о проецировании прямого угла
без искажения
• Плоскость. Способы задания плоскости. Плоскости
частного положения (уровня и проецирующие)
• Следы плоскости.
• Принадлежность точки и прямой плоскости.
• Главные линии плоскости.
• Определение угла наклона плоскости к плоскостям
проекций.
2.
Следы прямой линииСледом прямой
называется точка
пересечения прямой с
плоскостью проекций.
Н1 – горизонтальный след
прямой;
F2 – фронтальный след
прямой.
3.
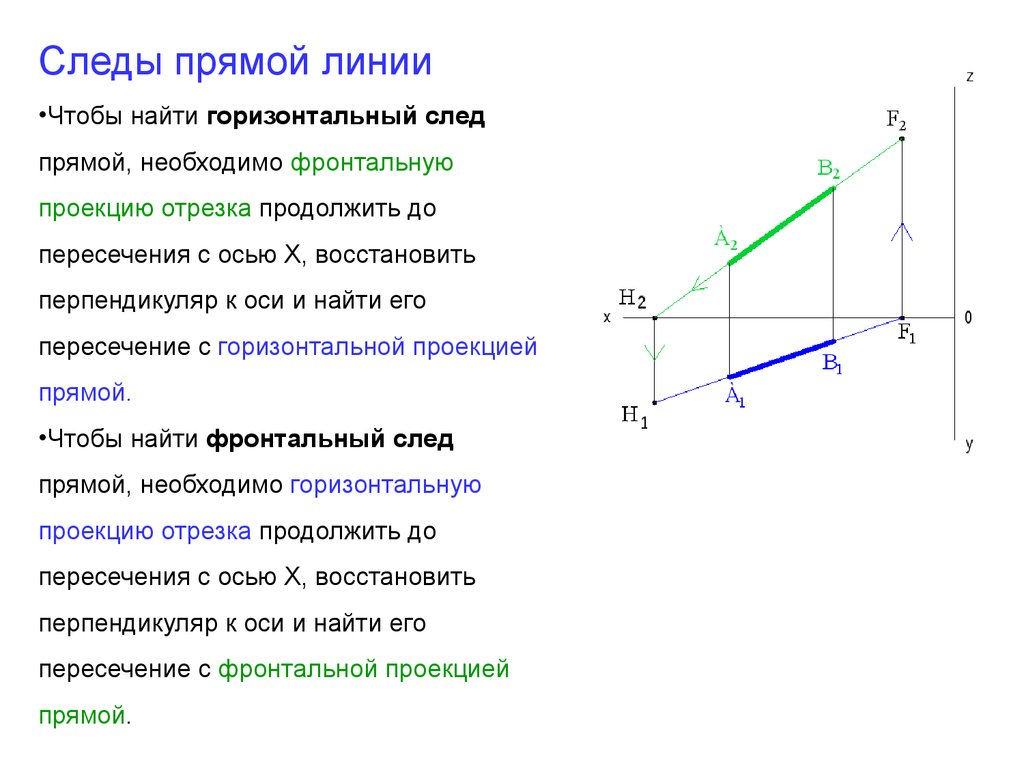
Следы прямой линии•Чтобы найти горизонтальный след
прямой, необходимо фронтальную
проекцию отрезка продолжить до
пересечения с осью Х, восстановить
перпендикуляр к оси и найти его
пересечение с горизонтальной проекцией
прямой.
•Чтобы найти фронтальный след
прямой, необходимо горизонтальную
проекцию отрезка продолжить до
пересечения с осью Х, восстановить
перпендикуляр к оси и найти его
пересечение с фронтальной проекцией
прямой.
4. Взаимное положение прямых
Прямые между собой могут быть:• Параллельны
• Пересекаться
• скрещиваться
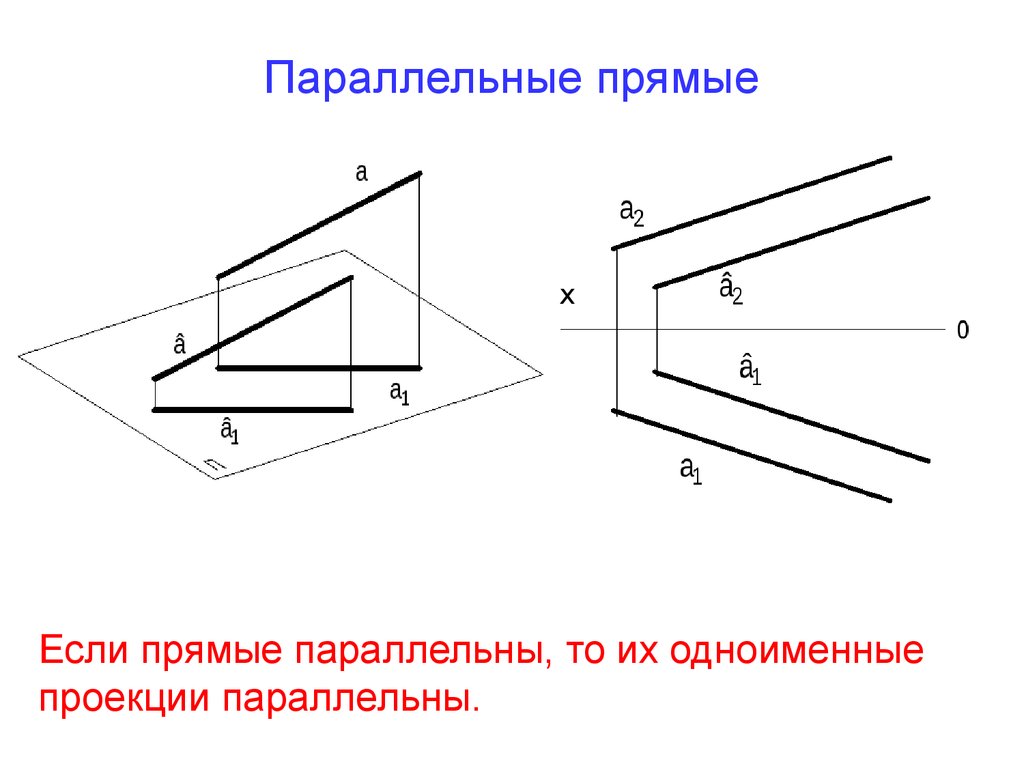
5. Параллельные прямые
хЕсли прямые параллельны, то их одноименные
проекции параллельны.
6.
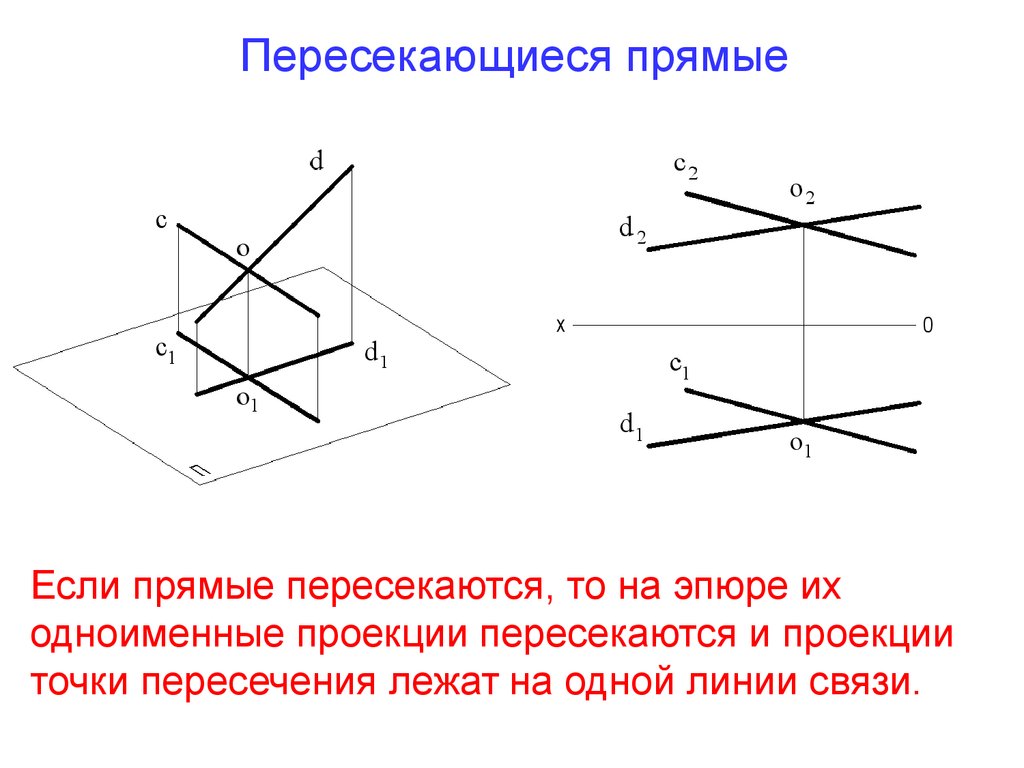
Пересекающиеся прямыеЕсли прямые пересекаются, то на эпюре их
одноименные проекции пересекаются и проекции
точки пересечения лежат на одной линии связи.
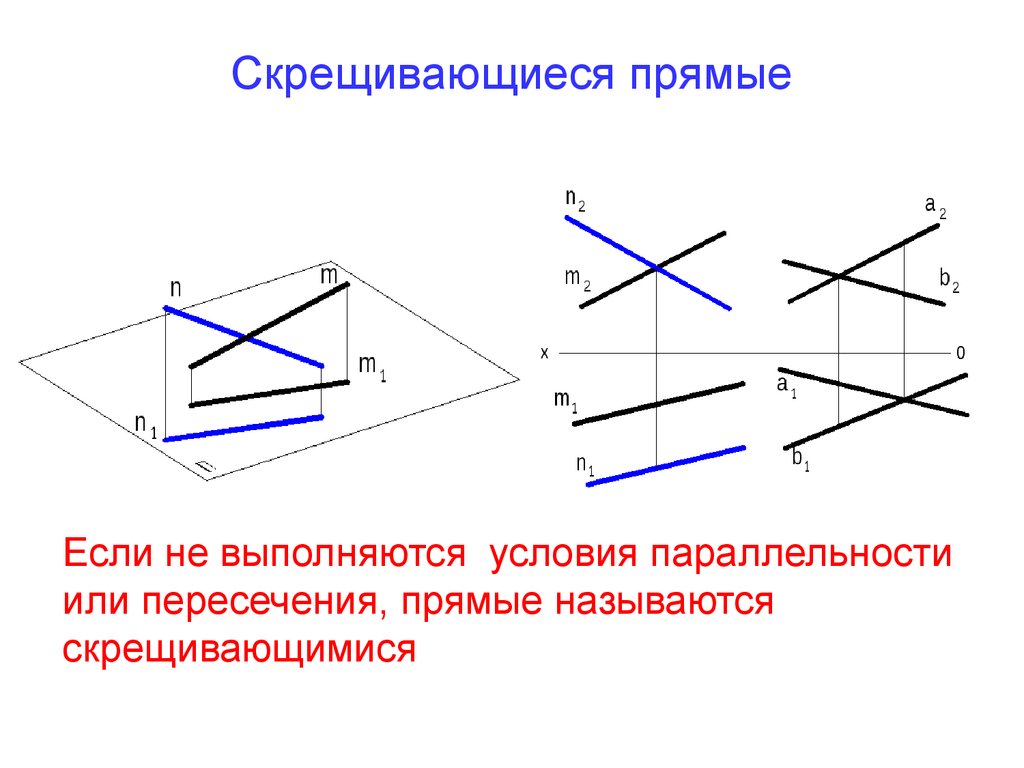
7. Скрещивающиеся прямые
Если не выполняются условия параллельностиили пересечения, прямые называются
скрещивающимися
8. Скрещивающиеся прямые
а)б)
12≡22
°
11
°
°
32
12≡22
°
°
°
°
° 42
11
°
21
31≡41
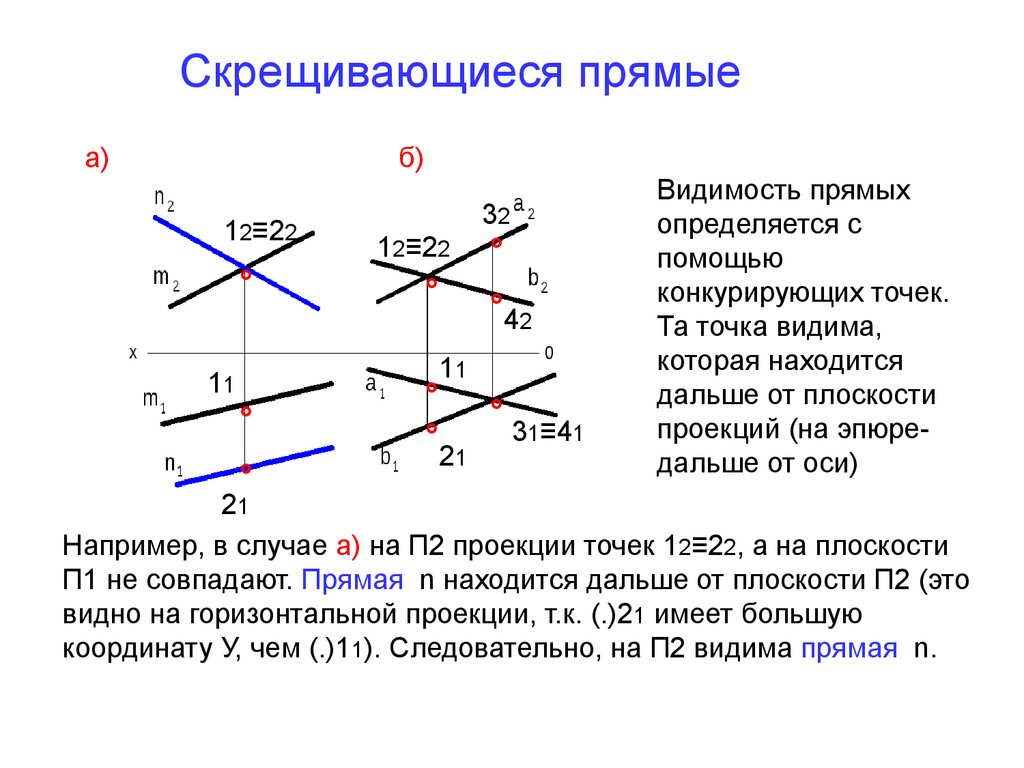
Видимость прямых
определяется с
помощью
конкурирующих точек.
Та точка видима,
которая находится
дальше от плоскости
проекций (на эпюредальше от оси)
21
Например, в случае а) на П2 проекции точек 12≡22, а на плоскости
П1 не совпадают. Прямая n находится дальше от плоскости П2 (это
видно на горизонтальной проекции, т.к. (.)21 имеет большую
координату У, чем (.)11). Следовательно, на П2 видима прямая n.
9.
Теорема о проецировании прямого углабез искажения
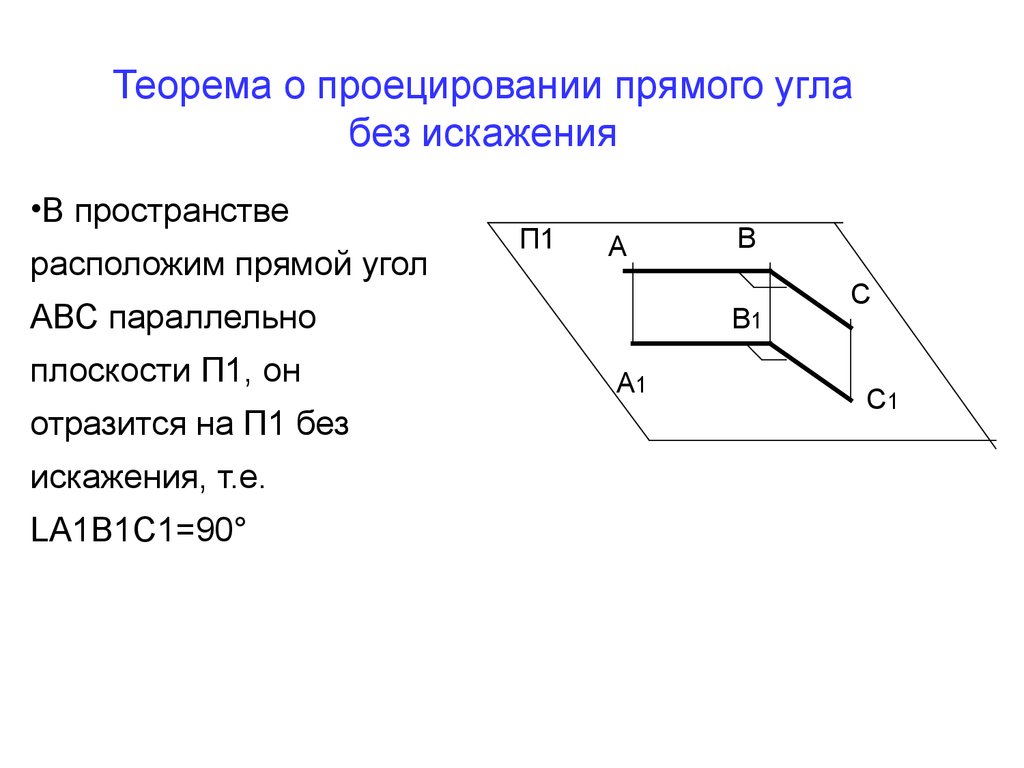
•В пространстве
расположим прямой угол
П1
А
АВС параллельно
плоскости П1, он
отразится на П1 без
искажения, т.е.
LА1В1С1=90°
В
В1
А1
С
С1
10.
Теорема о проецировании прямого углабез искажения
С*
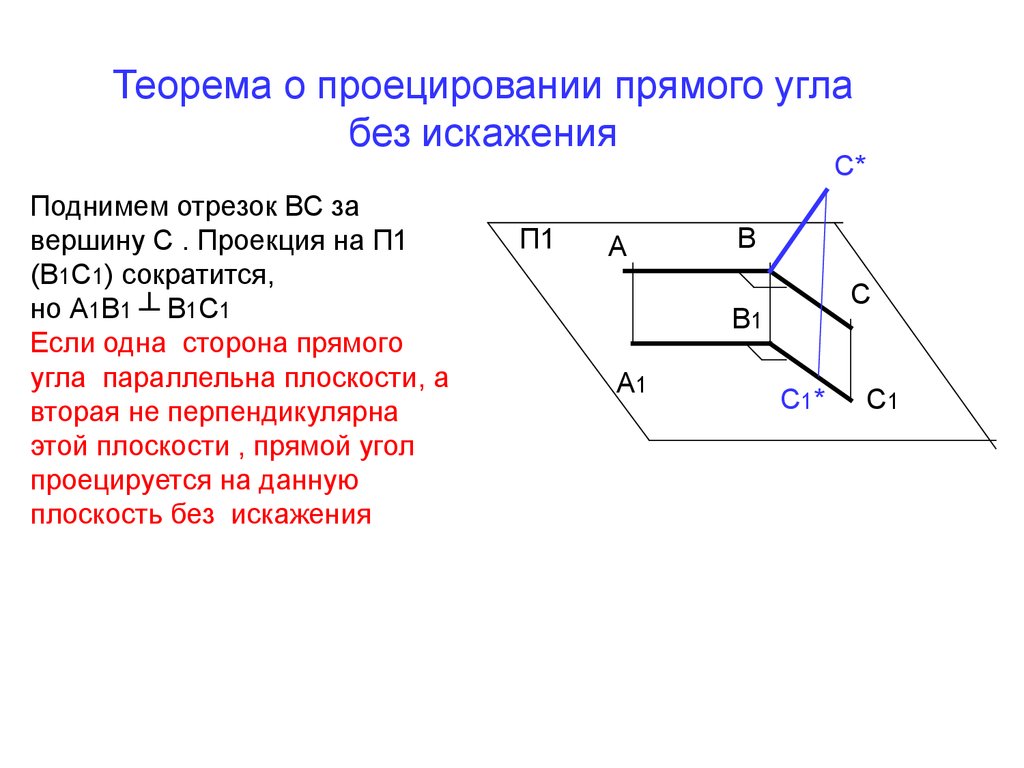
Поднимем отрезок ВС за
вершину С . Проекция на П1
(В1С1) сократится,
но А1В1 ┴ В1С1
Если одна сторона прямого
угла параллельна плоскости, а
вторая не перпендикулярна
этой плоскости , прямой угол
проецируется на данную
плоскость без искажения
П1
А
В
С
В1
А1
С 1*
С1
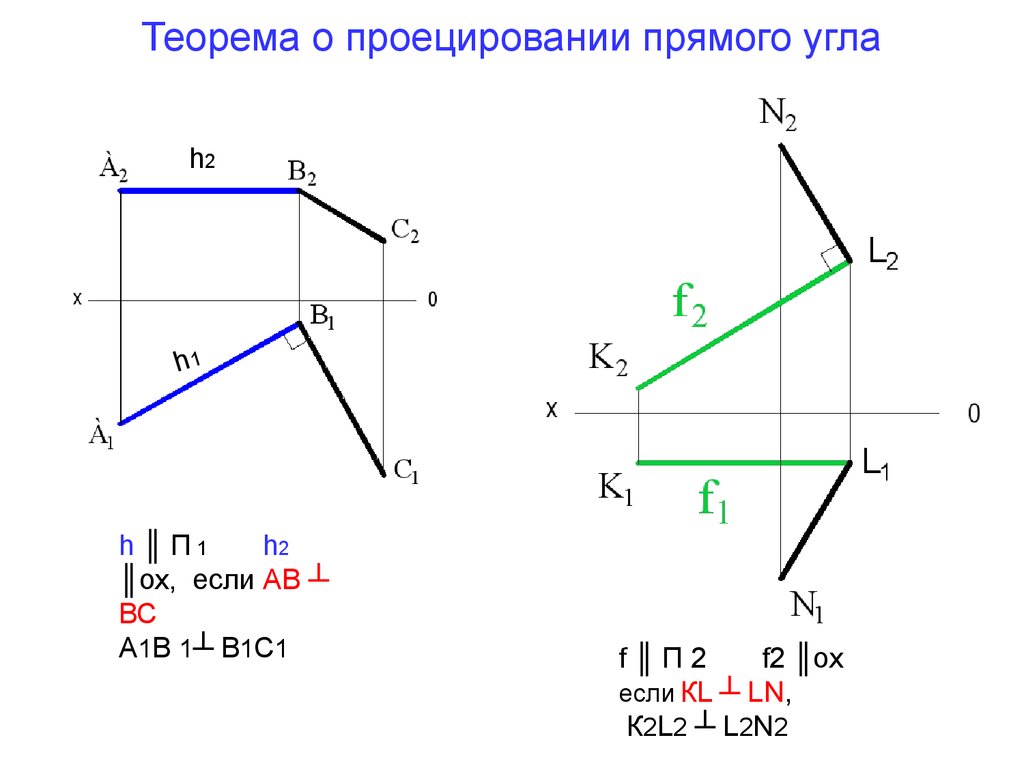
11. Теорема о проецировании прямого угла
h2h1
h ║ П1
h2
║ох, если АВ ┴
ВС
А1В 1┴ В1С1
f║П2
f2 ║ох
если КL ┴ LN,
К2L2 ┴ L2N2
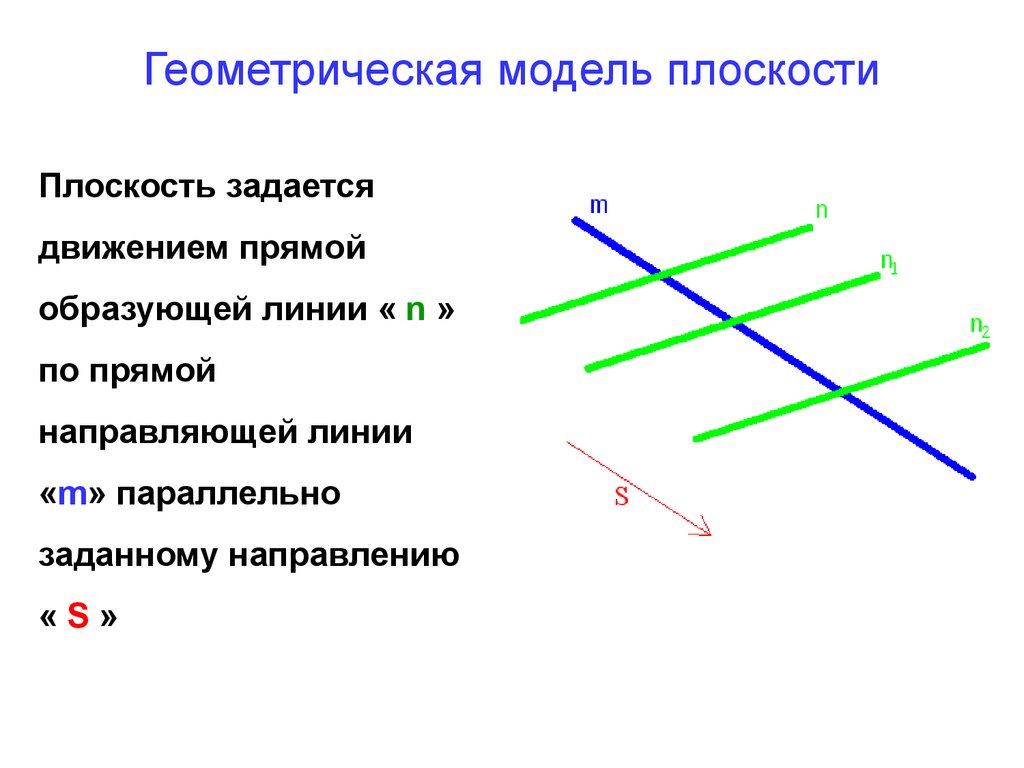
12. Геометрическая модель плоскости
Плоскость задаетсядвижением прямой
образующей линии « n »
по прямой
направляющей линии
«m» параллельно
заданному направлению
«S»
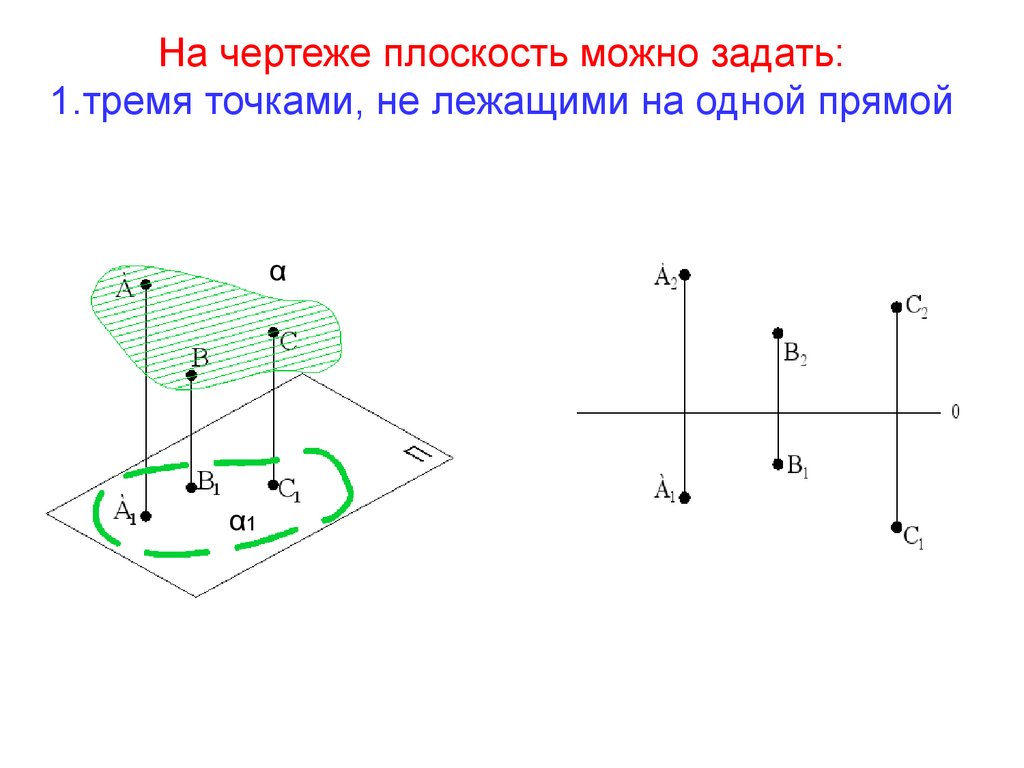
13. На чертеже плоскость можно задать: 1.тремя точками, не лежащими на одной прямой
αα1
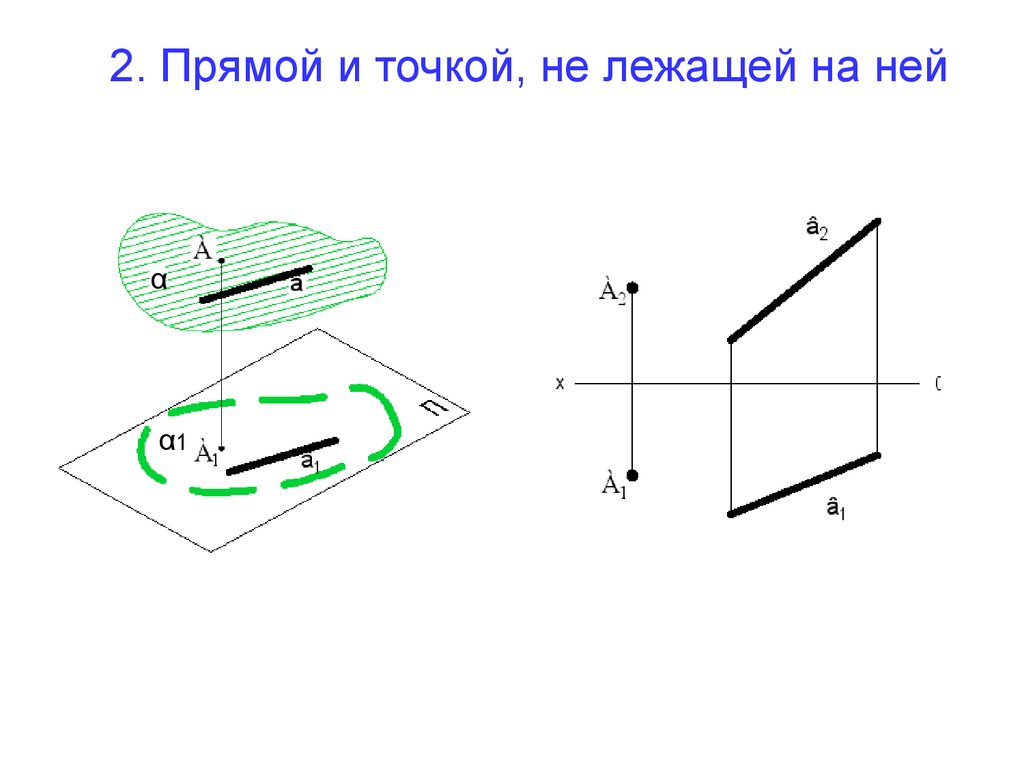
14. 2. Прямой и точкой, не лежащей на ней
αα1
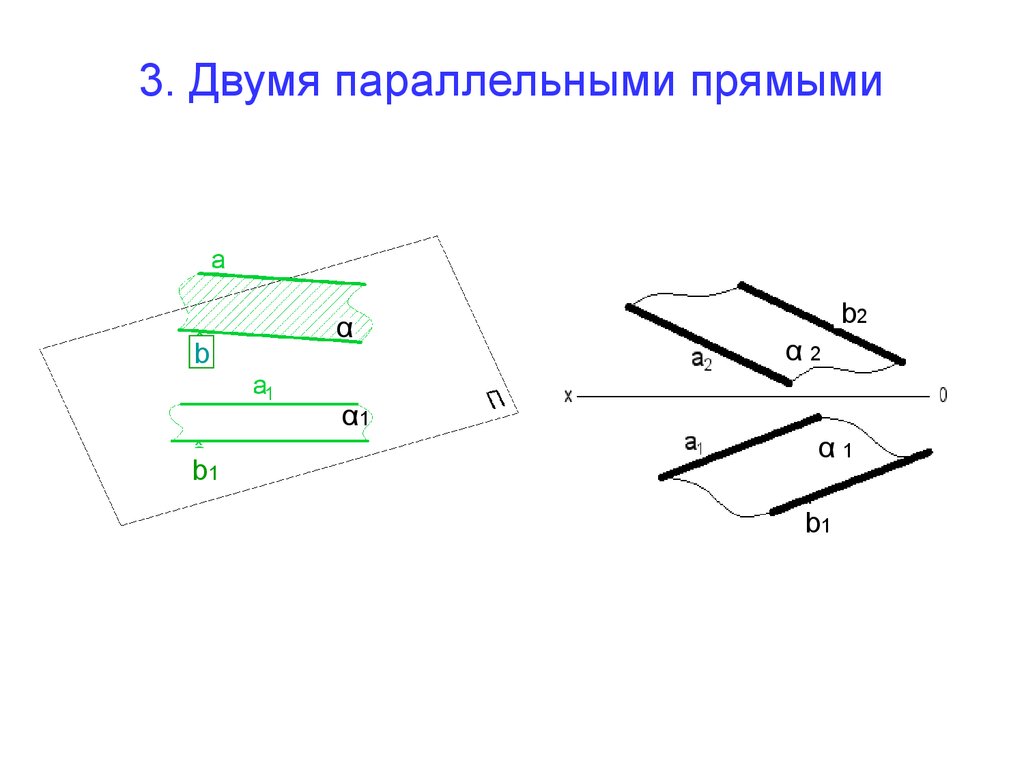
15. 3. Двумя параллельными прямыми
bα
b2
α2
α1
b1
α1
b1
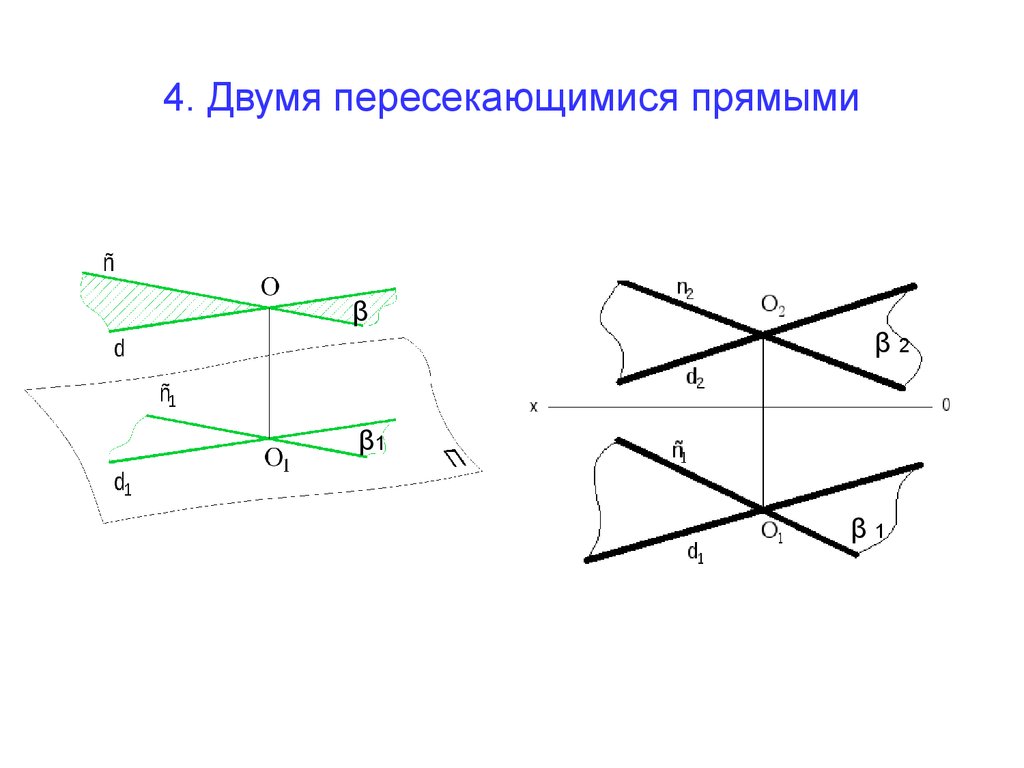
16. 4. Двумя пересекающимися прямыми
ββ2
β1
β1
17. 5. Отсеком плоской фигуры
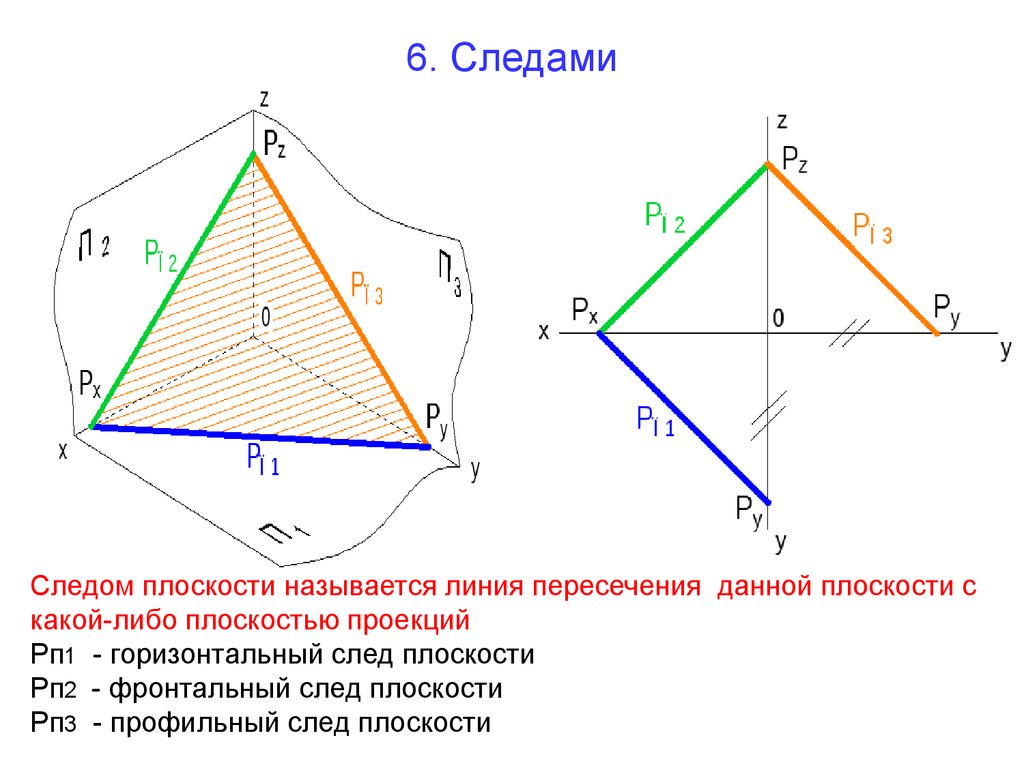
18. 6. Следами
Следом плоскости называется линия пересечения данной плоскости скакой-либо плоскостью проекций
Рп1 - горизонтальный след плоскости
Рп2 - фронтальный след плоскости
Рп3 - профильный след плоскости
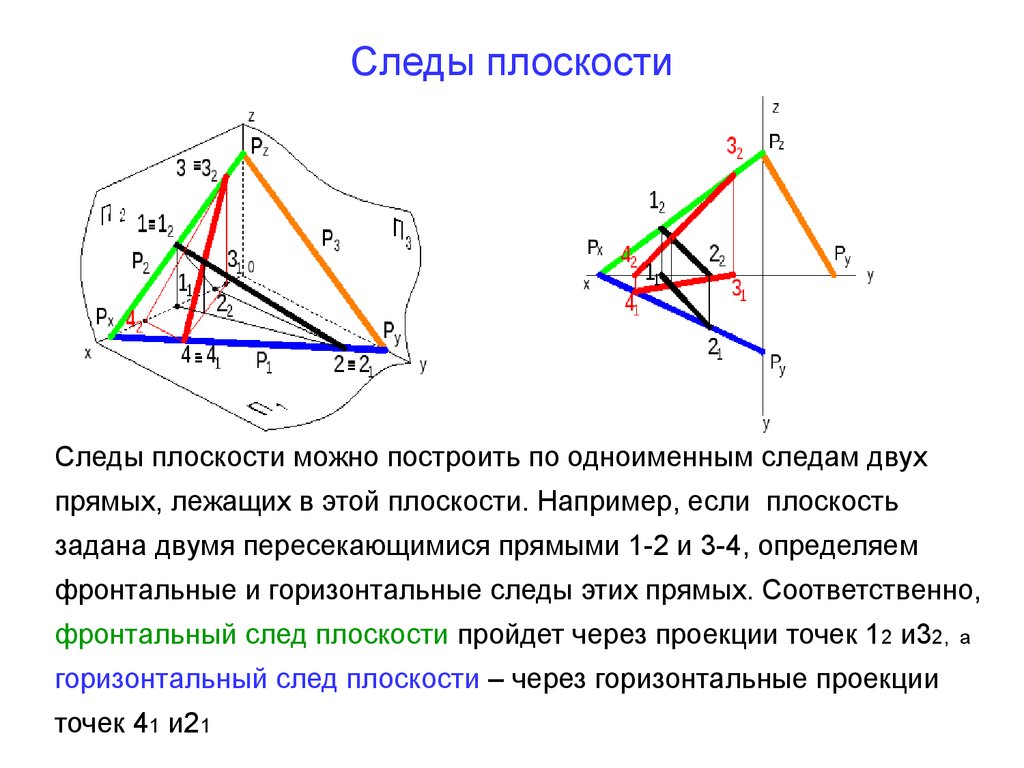
19. Следы плоскости
Следы плоскости можно построить по одноименным следам двухпрямых, лежащих в этой плоскости. Например, если плоскость
задана двумя пересекающимися прямыми 1-2 и 3-4, определяем
фронтальные и горизонтальные следы этих прямых. Соответственно,
фронтальный след плоскости пройдет через проекции точек 12 и32,
горизонтальный след плоскости – через горизонтальные проекции
точек 41 и21
а
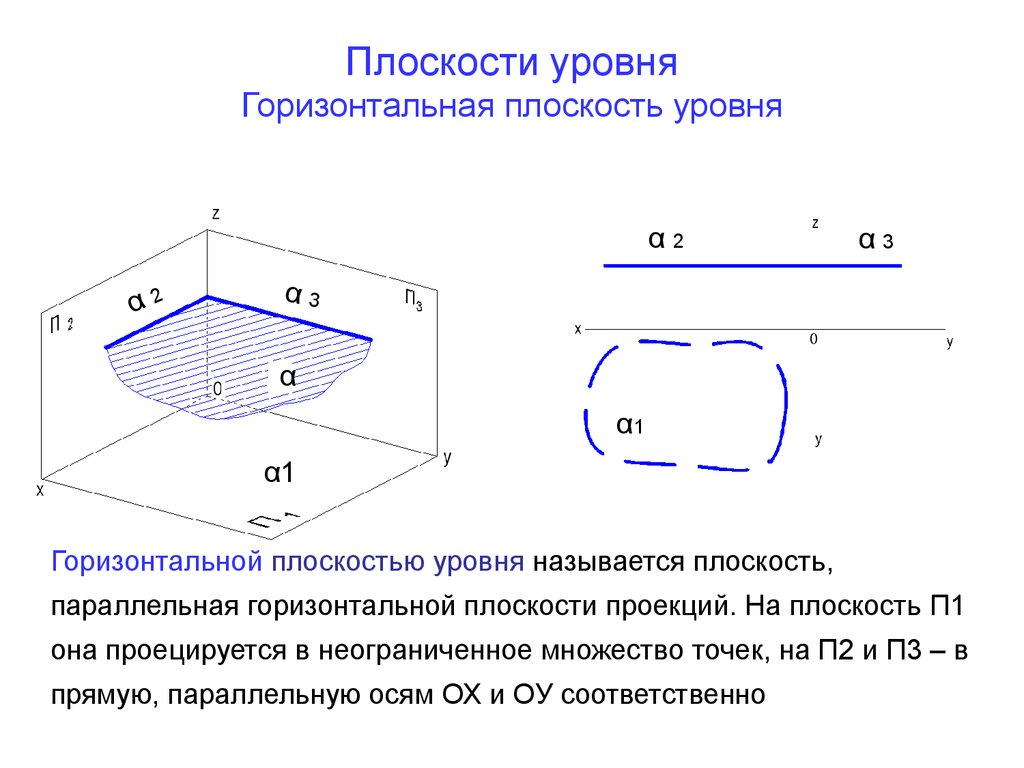
20. Плоскости уровня Горизонтальная плоскость уровня
α2α2
α3
α3
α
α1
α1
Горизонтальной плоскостью уровня называется плоскость,
параллельная горизонтальной плоскости проекций. На плоскость П1
она проецируется в неограниченное множество точек, на П2 и П3 – в
прямую, параллельную осям ОХ и ОУ соответственно
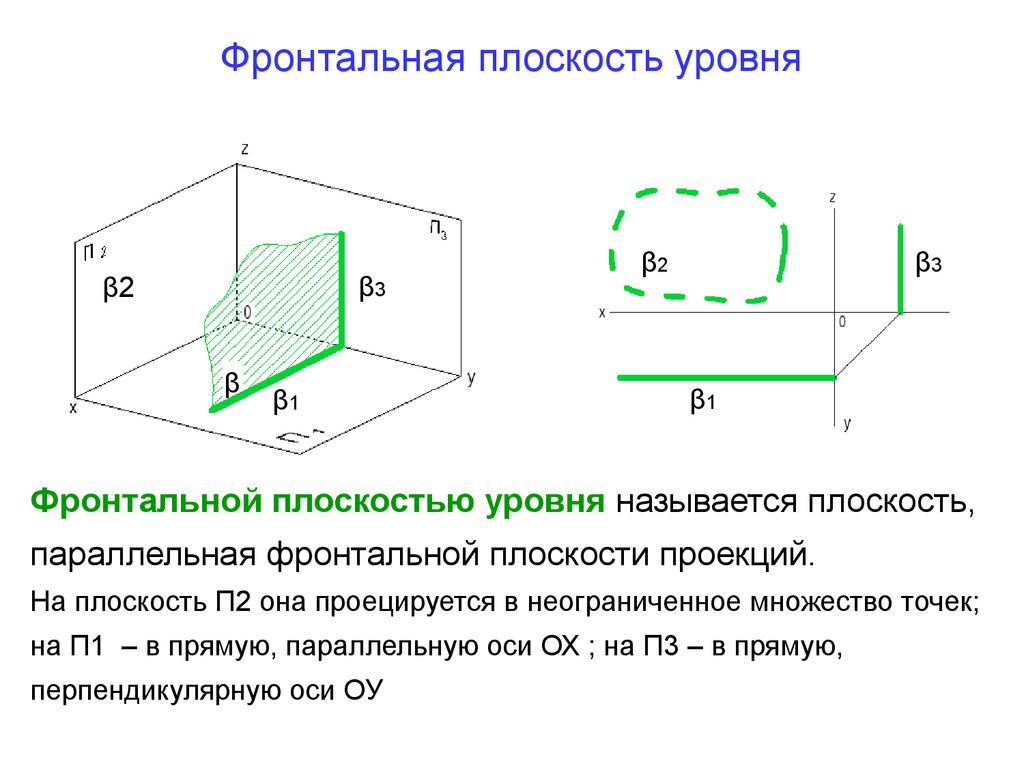
21. Фронтальная плоскость уровня
β3β2
β
β1
β2
β3
β1
Фронтальной плоскостью уровня называется плоскость,
параллельная фронтальной плоскости проекций.
На плоскость П2 она проецируется в неограниченное множество точек;
на П1 – в прямую, параллельную оси ОХ ; на П3 – в прямую,
перпендикулярную оси ОУ
22. Профильная плоскость уровня
γ3γ2
γ1
γ
γ2
γ3
γ1
Профильной плоскостью уровня называется плоскость,
параллельная профильной плоскости проекций.
На плоскость П3 она проецируется в неограниченное множество точек,
на П2 и П1 – в прямую, перпендикулярную оси ОХ
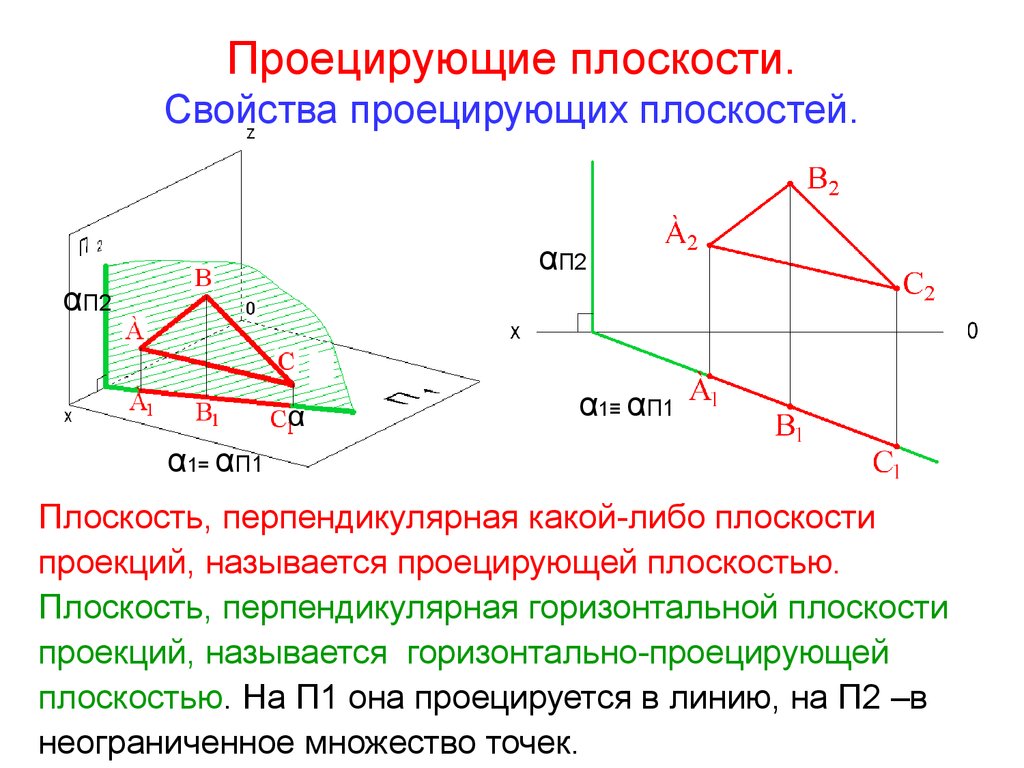
23. Проецирующие плоскости. Свойства проецирующих плоскостей.
αП2αП2
α
α1≡ αП1
α1= αП1
Плоскость, перпендикулярная какой-либо плоскости
проекций, называется проецирующей плоскостью.
Плоскость, перпендикулярная горизонтальной плоскости
проекций, называется горизонтально-проецирующей
плоскостью. На П1 она проецируется в линию, на П2 –в
неограниченное множество точек.
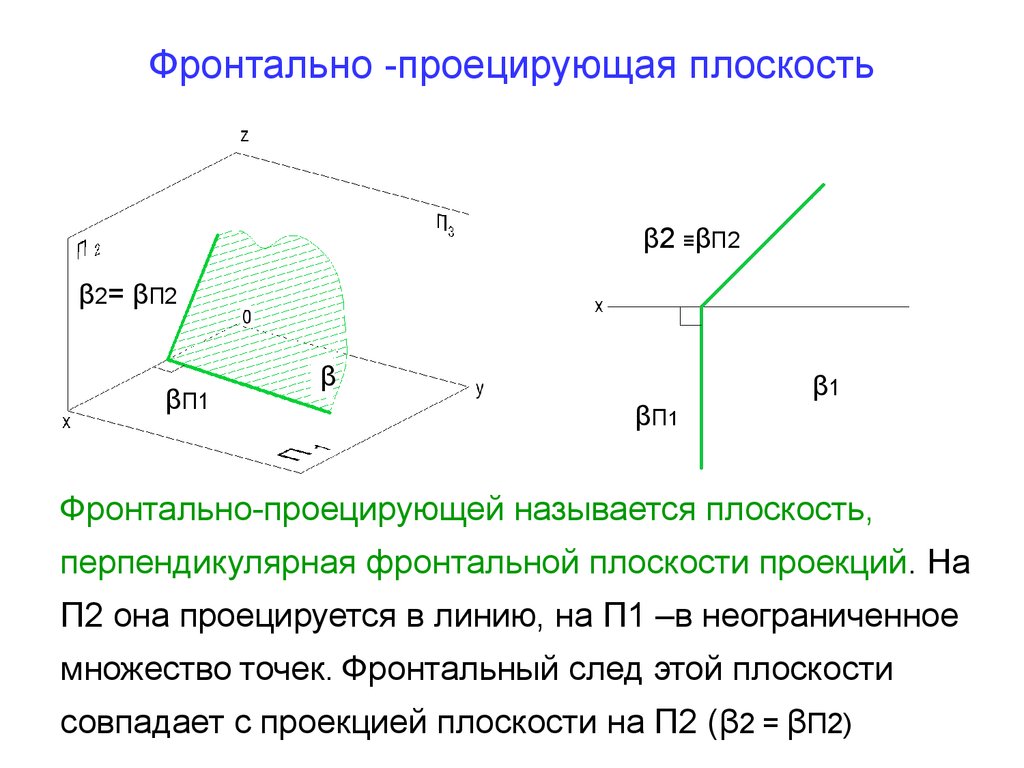
24. Фронтально -проецирующая плоскость
β2 ≡βП2β2= βП2
βП1
β
βП1
β1
Фронтально-проецирующей называется плоскость,
перпендикулярная фронтальной плоскости проекций. На
П2 она проецируется в линию, на П1 –в неограниченное
множество точек. Фронтальный след этой плоскости
совпадает с проекцией плоскости на П2 (β2 = βП2)
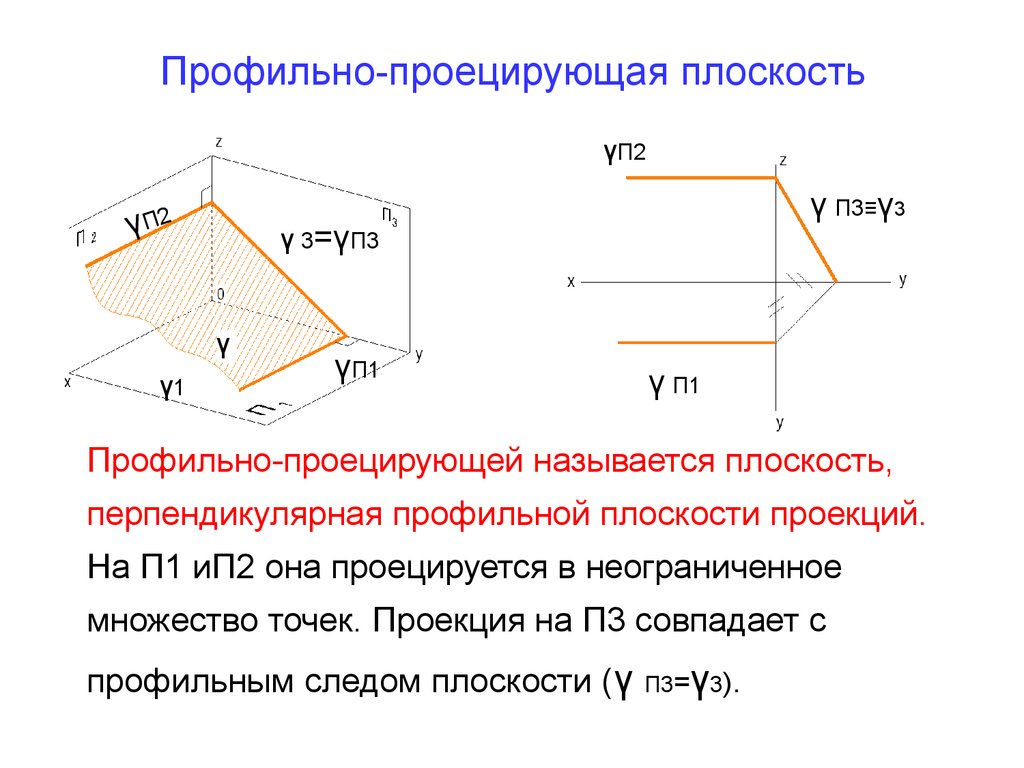
25. Профильно-проецирующая плоскость
γП2γП2
γ 3=γП3
γ
γ1
γ П3≡γ3
γП1
γ П1
Профильно-проецирующей называется плоскость,
перпендикулярная профильной плоскости проекций.
На П1 иП2 она проецируется в неограниченное
множество точек. Проекция на П3 совпадает с
профильным следом плоскости (γ
γ
П3= 3).
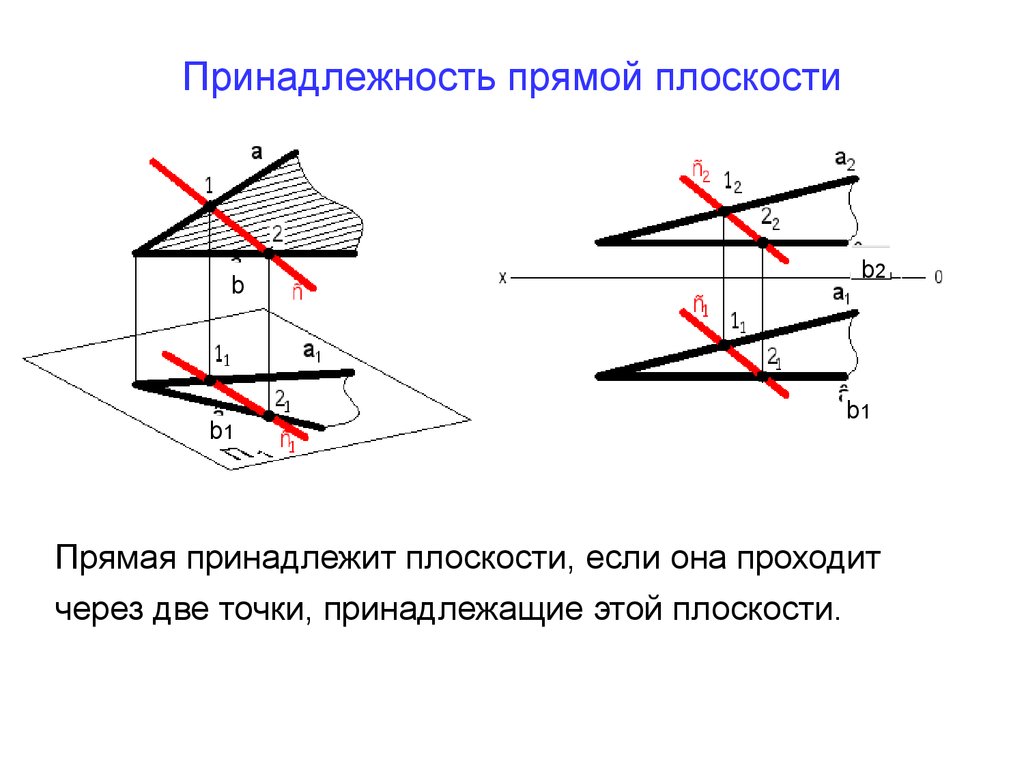
26. Принадлежность прямой плоскости
bb1
b2
b1
Прямая принадлежит плоскости, если она проходит
через две точки, принадлежащие этой плоскости.
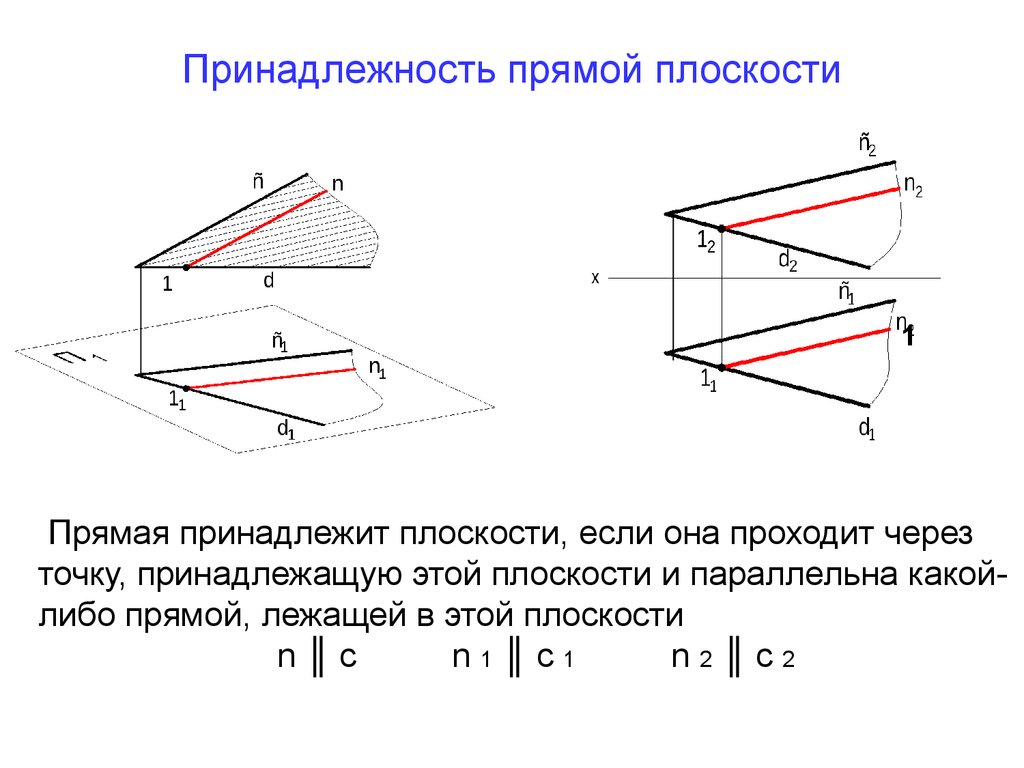
27. Принадлежность прямой плоскости
1Прямая принадлежит плоскости, если она проходит через
точку, принадлежащую этой плоскости и параллельна какойлибо прямой, лежащей в этой плоскости
n║c
n1║c1
n2║c2
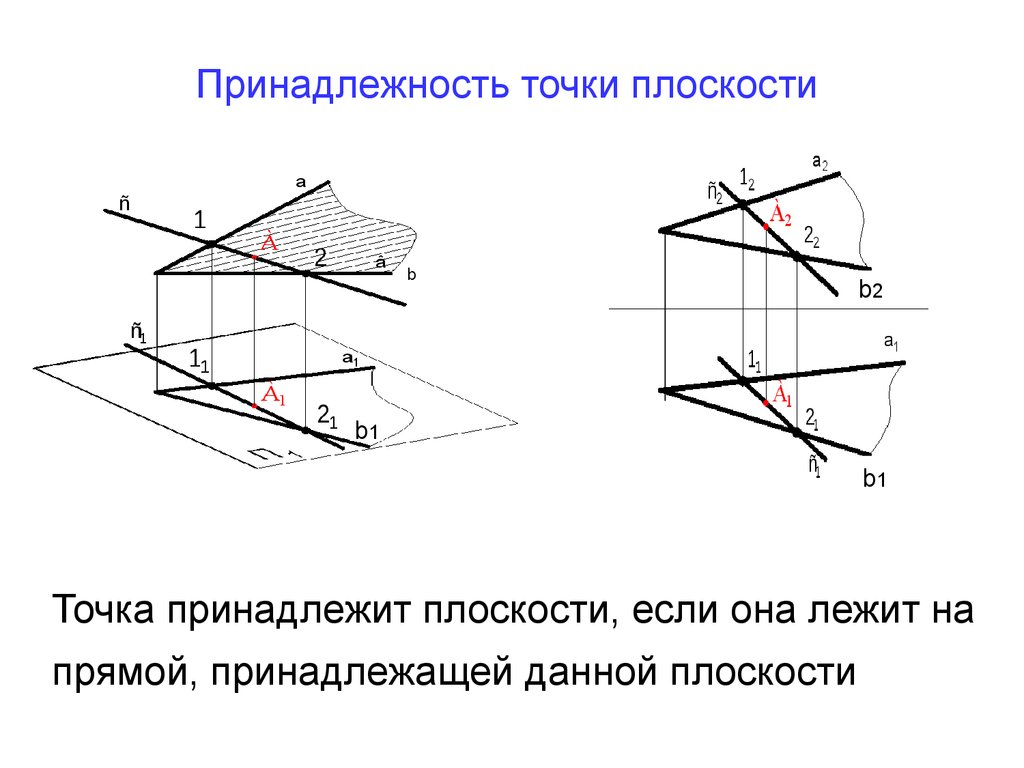
28. Принадлежность точки плоскости
bb2
b1
b1
Точка принадлежит плоскости, если она лежит на
прямой, принадлежащей данной плоскости
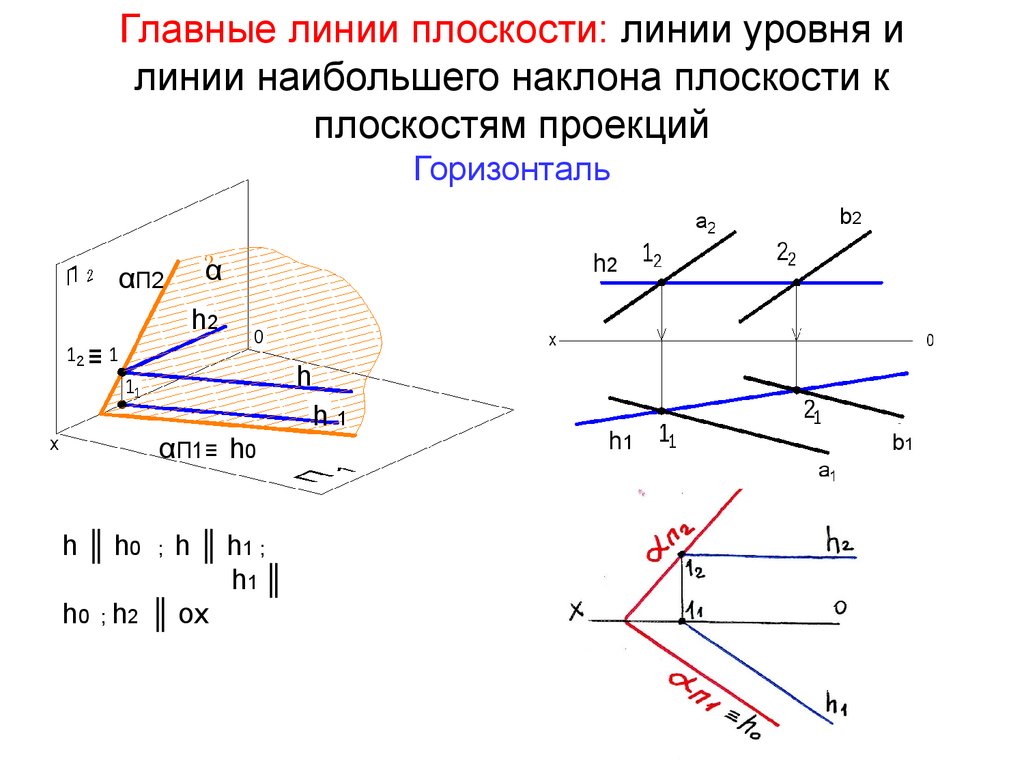
29. Главные линии плоскости: линии уровня и линии наибольшего наклона плоскости к плоскостям проекций Горизонталь
b2αП2
h2
α
h2
h
h1
αП1≡ h0
h ║ h0
h ║ h1 ;
h1 ║
h0 ; h2 ║ ох
;
h1
b1
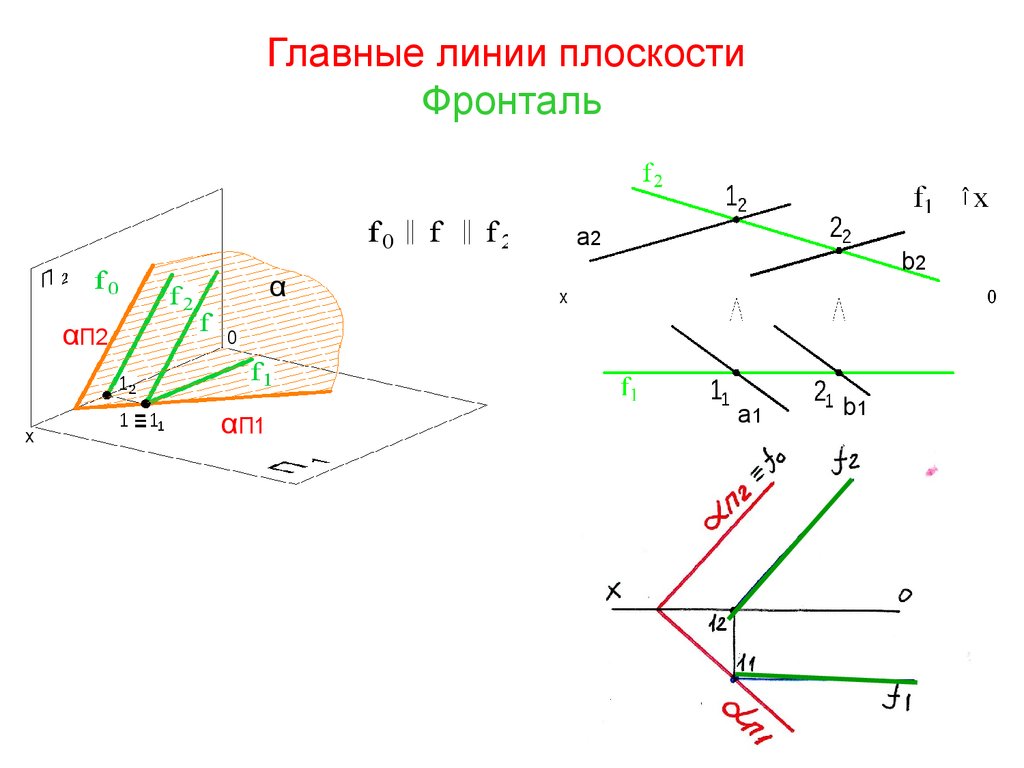
30. Главные линии плоскости Фронталь
a2b2
α
αП2
αП1
a1
b1
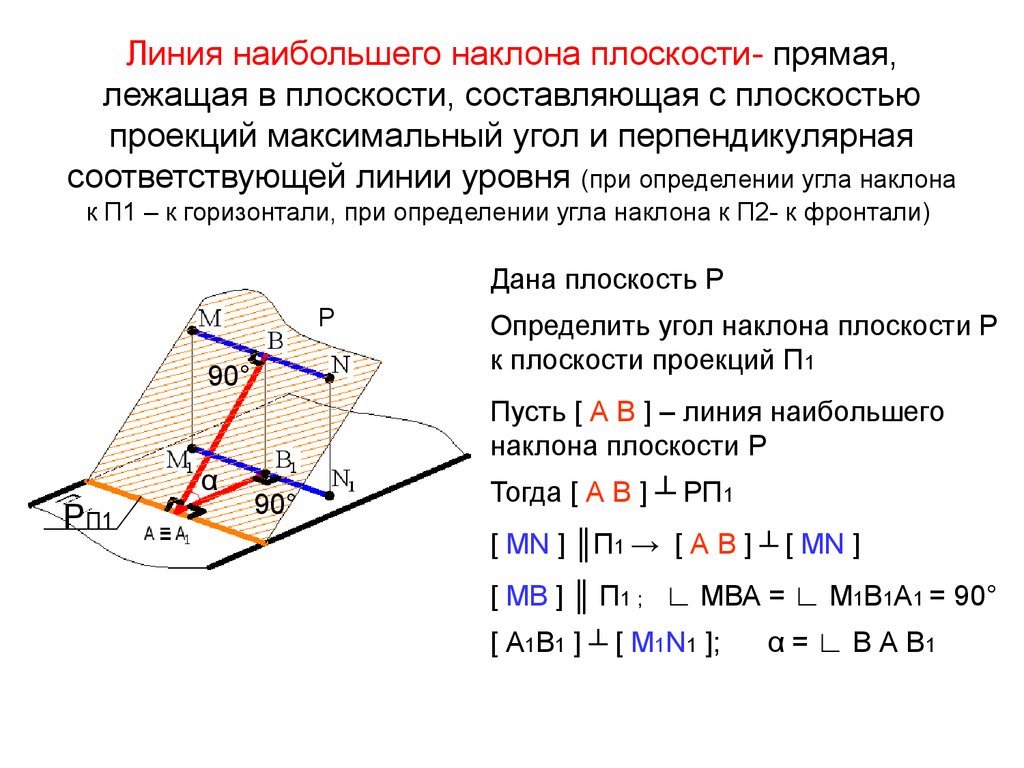
31. Линия наибольшего наклона плоскости- прямая, лежащая в плоскости, составляющая с плоскостью проекций максимальный угол и перпендикулярна
Линия наибольшего наклона плоскости- прямая,лежащая в плоскости, составляющая с плоскостью
проекций максимальный угол и перпендикулярная
соответствующей линии уровня (при определении угла наклона
к П1 – к горизонтали, при определении угла наклона к П2- к фронтали)
Дана плоскость Р
Р
90°
Определить угол наклона плоскости Р
к плоскости проекций П1
Пусть [ А В ] – линия наибольшего
наклона плоскости Р
α
РП1
90°
Тогда [ А В ] ┴ РП1
[ MN ] ║П1 → [ А В ] ┴ [ MN ]
[ МВ ] ║ П1 ; ∟ МВА = ∟ М1В1А1 = 90°
[ А1В1 ] ┴ [ M1N1 ];
α = ∟ В А В1
32. Определение угла наклона плоскости общего положения к плоскости проекций
• Угол наклона плоскости общего положения ккакой-либо плоскости проекций равен углу
между натуральной величиной линии
наибольшего наклона плоскости и ее
проекцией на заданную плоскость проекций.
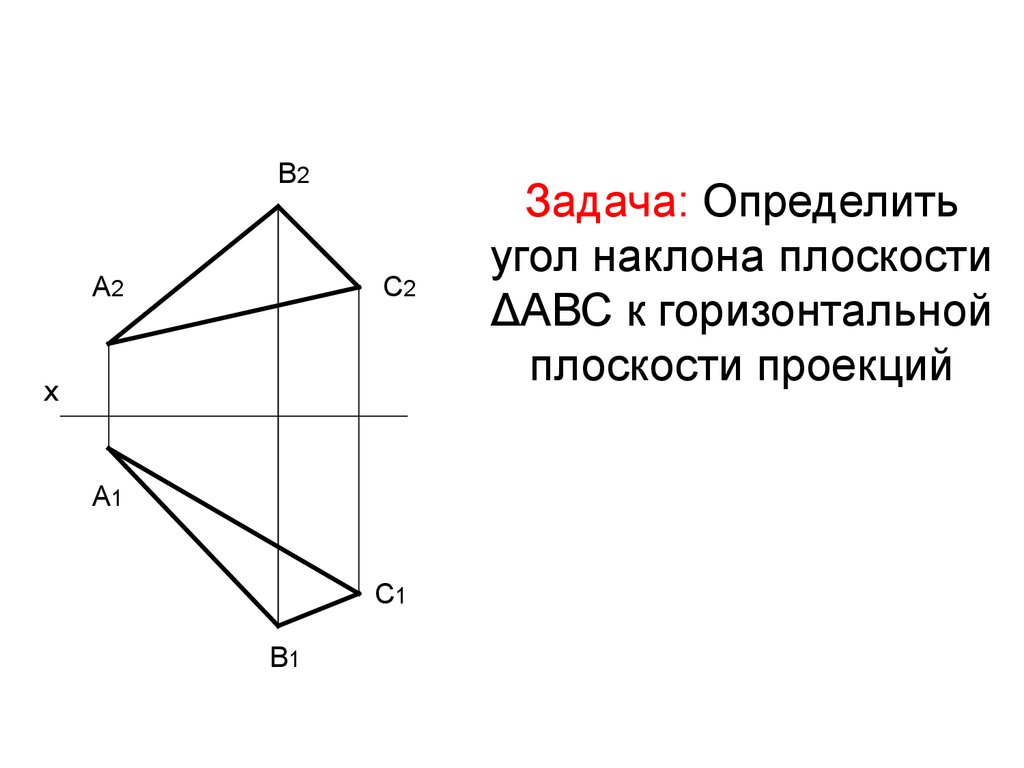
33. Задача: Определить угол наклона плоскости ΔАВС к горизонтальной плоскости проекций
В2А2
С2
х
А1
С1
В1
Задача: Определить
угол наклона плоскости
ΔАВС к горизонтальной
плоскости проекций
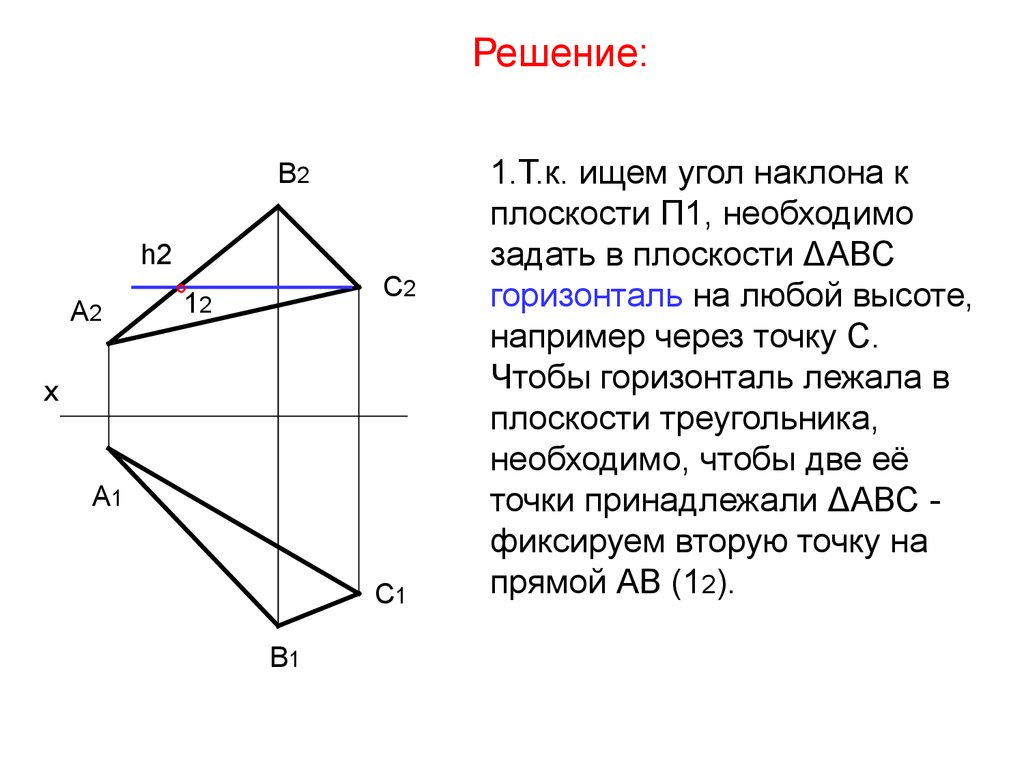
34. 1.Т.к. ищем угол наклона к плоскости П1, необходимо задать в плоскости ΔАВС горизонталь на любой высоте, например через точку С. Чтобы горизон
Решение:В2
h2
А2
С2
°12
х
А1
С1
В1
1.Т.к. ищем угол наклона к
плоскости П1, необходимо
задать в плоскости ΔАВС
горизонталь на любой высоте,
например через точку С.
Чтобы горизонталь лежала в
плоскости треугольника,
необходимо, чтобы две её
точки принадлежали ΔАВС фиксируем вторую точку на
прямой АВ (12).
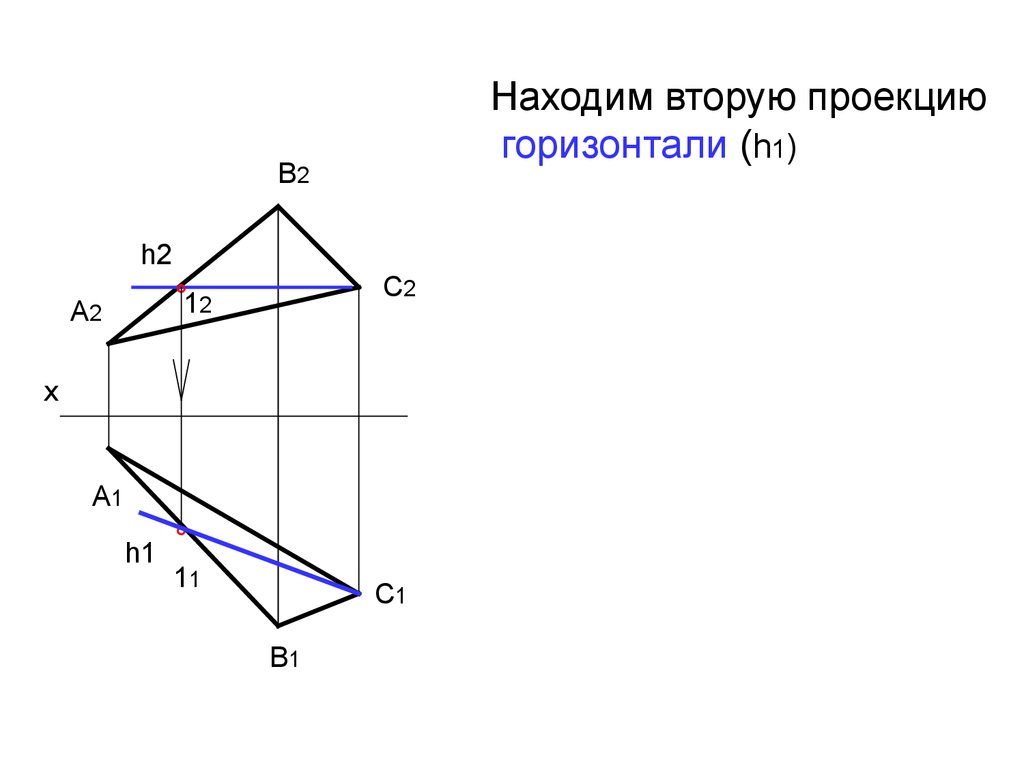
35. Находим вторую проекцию горизонтали (h1)
В2h2
С2
°12
А2
х
А1
h1
°
11
С1
В1
36. 2. Линия наибольшего наклона (Л.Н.Н.) плоскости (ВО) перпендикулярна к горизонталям данной плоскости. Следовательно, можно построить проекци
В2h2
С2
°12
А2
х
А1
h1
°
11
О1
°
°
В1
С1
Л.н.н.
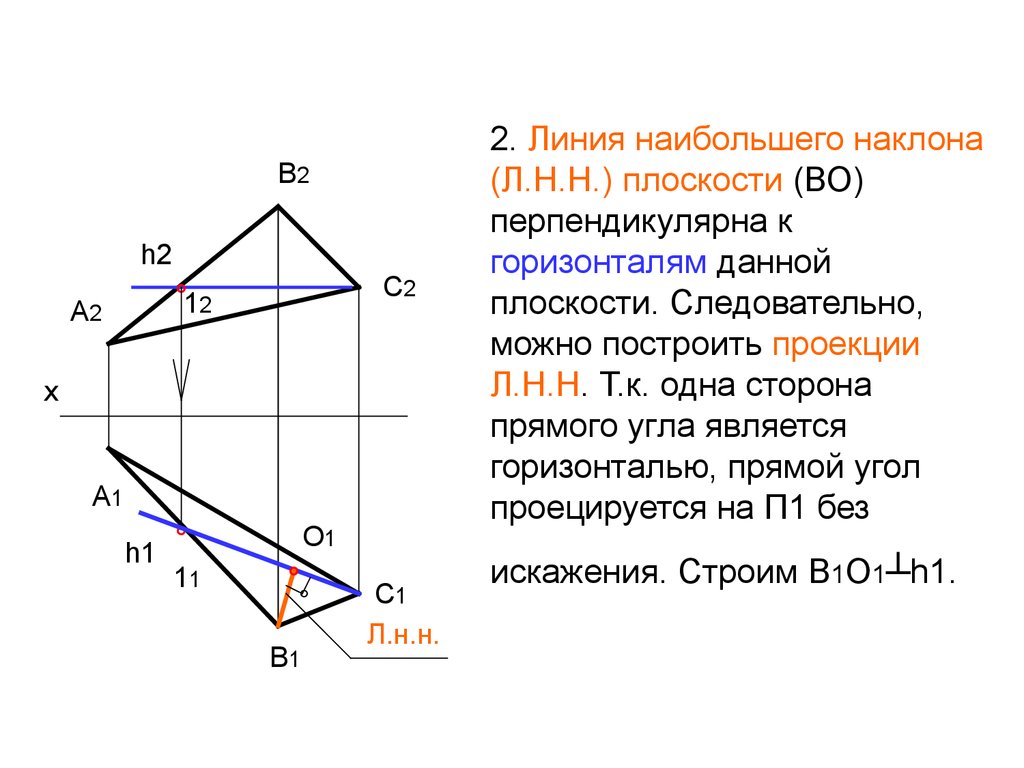
2. Линия наибольшего наклона
(Л.Н.Н.) плоскости (ВО)
перпендикулярна к
горизонталям данной
плоскости. Следовательно,
можно построить проекции
Л.Н.Н. Т.к. одна сторона
прямого угла является
горизонталью, прямой угол
проецируется на П1 без
искажения. Строим В1О1┴h1.
37. Определяем по линии связи фронтальную проекцию(.)О - О2. В2О2 – фронтальная проекция линии наибольшего наклона плоскости к П1(линии ската)
В2h2
°12
А2
О2
°
С2
х
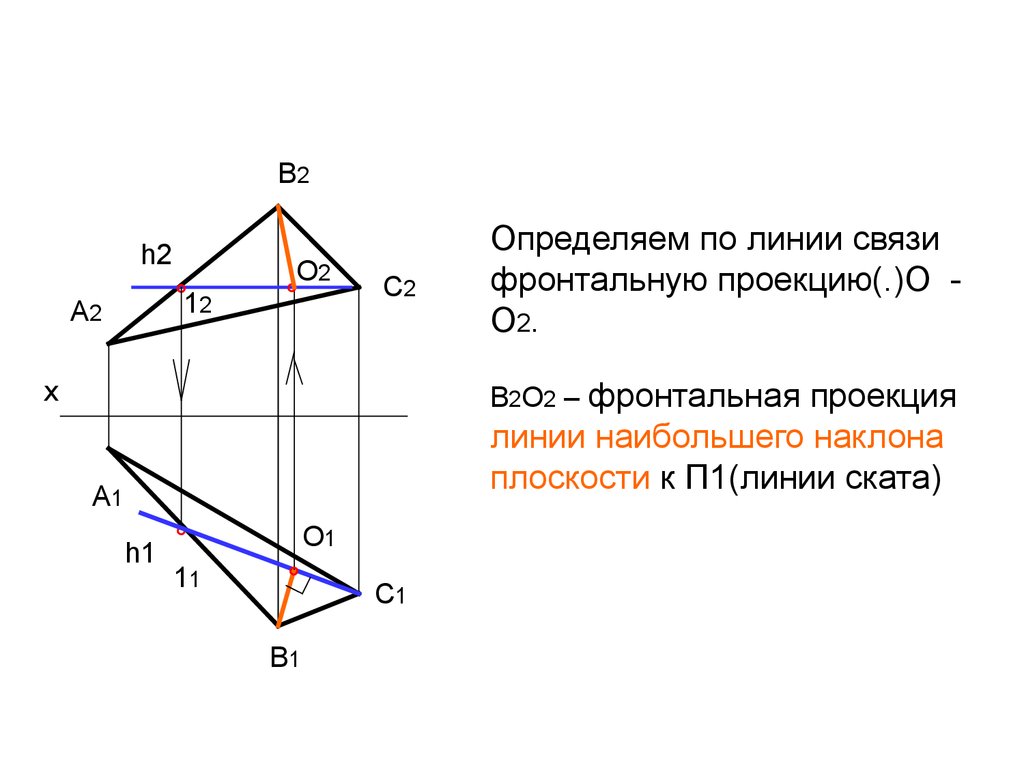
Определяем по линии связи
фронтальную проекцию(.)О О2.
В2О2 – фронтальная
проекция
линии наибольшего наклона
плоскости к П1(линии ската)
А1
h1
°
11
О1
°
В1
С1
38. Угол наклона плоскости общего положения к плоскости П1 равен углу между линией наибольшего наклона и её горизонтальной проекцией. Следова
В2Δz
h2
°12
А2
О2
°
С2
х
А1
h1
°
11
О1
°
В1
С1
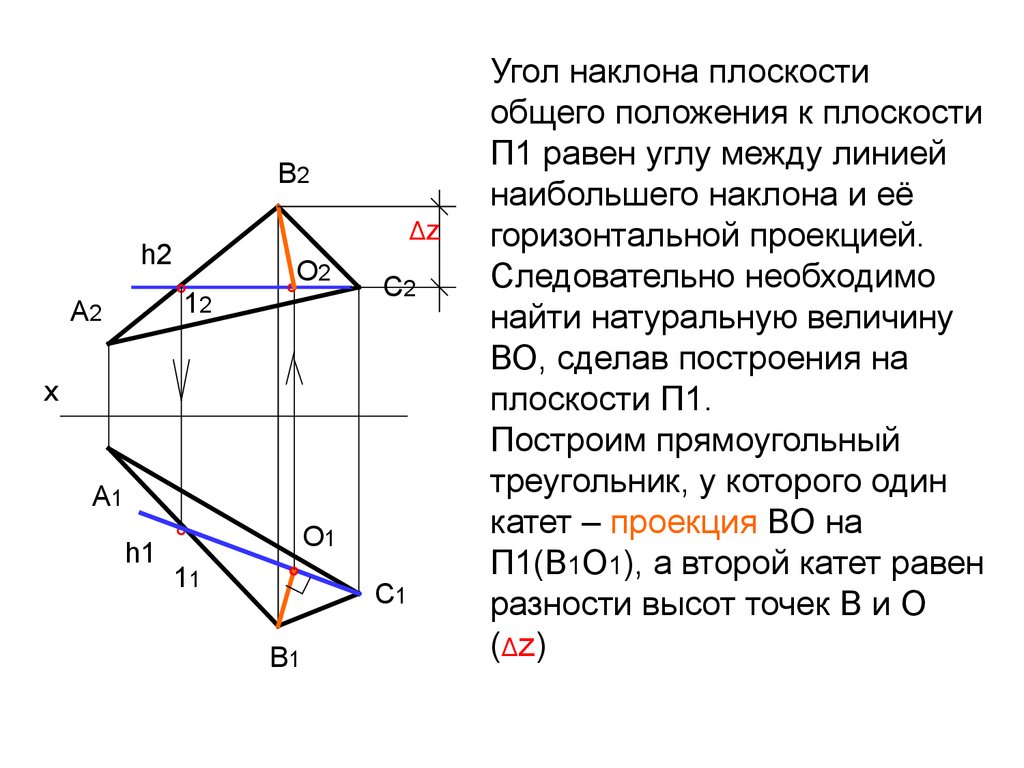
Угол наклона плоскости
общего положения к плоскости
П1 равен углу между линией
наибольшего наклона и её
горизонтальной проекцией.
Следовательно необходимо
найти натуральную величину
ВО, сделав построения на
плоскости П1.
Построим прямоугольный
треугольник, у которого один
катет – проекция ВО на
П1(В1О1), а второй катет равен
разности высот точек В и О
(Δz)
39. Натуральная величина отрезка ВО- гипотенуза треугольника. Угол наклона плоскости ΔАВС к плоскости П1- угол α (величину которого можно измер
В2Δz
h2
°12
А2
О2
°
С2
х
Δz
А1
h1
°
11
Н.в.[ВО]
О1
α °
В1
С1
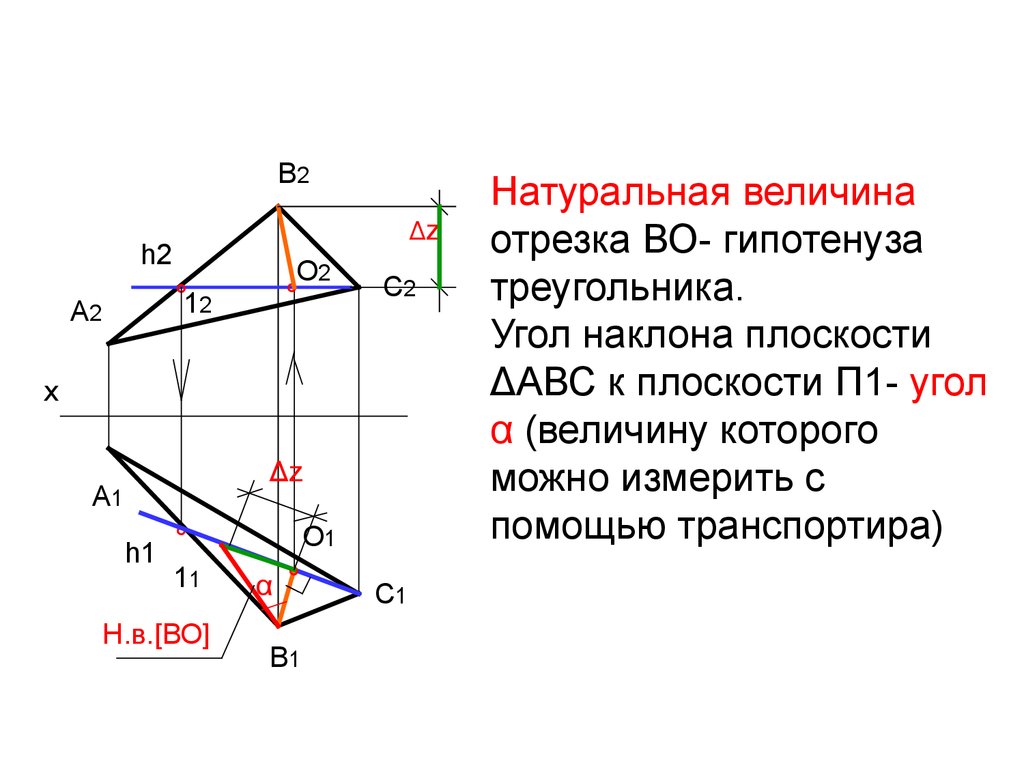
Натуральная величина
отрезка ВО- гипотенуза
треугольника.
Угол наклона плоскости
ΔАВС к плоскости П1- угол
α (величину которого
можно измерить с
помощью транспортира)






 Инженерная графика
Инженерная графика








