Линейная и векторная алгебра

1. Линейная и векторная алгебра

матрицы
определители
обратная матрица
ранг матрицы
системы линейных уравнений
элементы векторной алгебры

2. матрицы

Определение матрицы
Виды матрицы
Равенство матриц
Сложение матриц
Умножение матрицы на число
Умножение матриц

3. Определение матрицы

Общий вид записи
матрицы из m x n чисел:
a11
a21
D
BA ...
C
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
Прямоугольная таблица,
составленная из m x n чисел,
называется матрицей.
Для обозначения матрицы
применяются круглые
скобки и прописные буквы A,
B, C …
Числа a11, a12, … , amn,
составляющие матрицу,
называются
её элементами.

4.

Горизонтальные ряды матрицы называются строками
матрицы
вертикальные - столбцами.
Индексы i и j элемента aij, где i=1, 2, …, m, j=1,2, ..., n,
означают, что этот элемент расположен в i-й строке и j-м
столбце.
A
a11
a 21
...
am 1
a12
a 22
...
am 2
...
...
aij...
...
a1 n
a2 n
...
a mn
Матрица обозначается также в форме A(aij)mxn, где i=1, 2, …,
m, j=1, 2, …, n.

5. Виды матриц

Квадратная матрица
Диагональная матрица
Единичная матрица
Матрица-строка и матрица-столбец
Транспонированная матрица

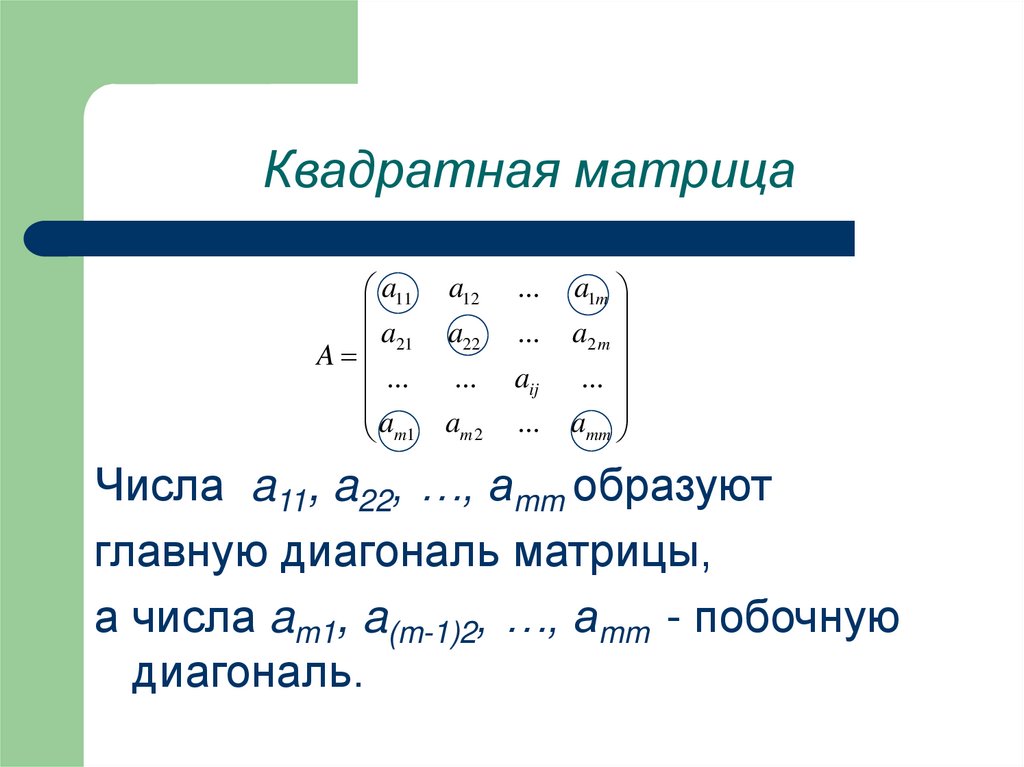
6. Квадратная матрица

Матрица, у которой
a11 a12
число строк равно
a21 a22
числу ее столбцов
a11
называется
квадратной матрицей.
a21
При этом число ее
a
строк (столбцов)
31
называется порядком a11 a12 a13 a14
матрицы.
a21 a22 a23 a24
a
a32
31
a
41 a42
a33
a43
a34
a44
a12
a22
a32
a13
a23
a33

7. Квадратная матрица

a11
a21
A
...
am1
a12
...
a22
...
...
aij
am 2
...
a1m
a2 m
...
amm
Числа a11, a22, …, amm образуют
главную диагональ матрицы,
а числа am1, a(m-1)2, …, amm - побочную
диагональ.

8. Диагональная матрица

Квадратная матрица,
у которой
все числа, не стоящие
на главной диагонали,
равны нулю,
называется
диагональной
матрицей.
a11
0
A
0
0
0
0
a22
0
0
aii
0
0
0
0
0
amm

9. ЕДИНИЧНАЯ МАТРИЦА

Диагональная
матрица, у которой
все элементы главной
диагонали равны
единице,
называется
единичной
матрицей.
Единичную матрицу
обозначают
прописной буквой Е.
1
0
E
...
0
Е
0 ... 0
1 ... 0
... ... ...
0 ... 1

10. Матрица-строка

Матрица-столбец
Матрица, состоящая
только
из одной строки,
называется
матрицей-строкой.
A a11 a12 ... a1n
Матрица, состоящая
только
из одной строки,
называется
матрицей-столбцом.
a11
a21
A
...
a
m1

11. Транспонированная матрица

Матрица называется
транспонированной
по отношению к
матрице А, если
столбцы матрицы
являются
соответствующими
строчками матрицы.
a11
a21
A
...
a
m1
a11
a12
T
A
...
a1n
a12
a22
...
am 2
a21
a22
...
a2 n
... a1n
... a2 n
... ...
... amn
... am1
... am 2
... ...
... anm

12. РАВЕНСТВО МАТРИЦ

Две матрицы А и В называются равными
(A=B), если они имеют одинаковые
размеры и равные соответствующие
элементы.

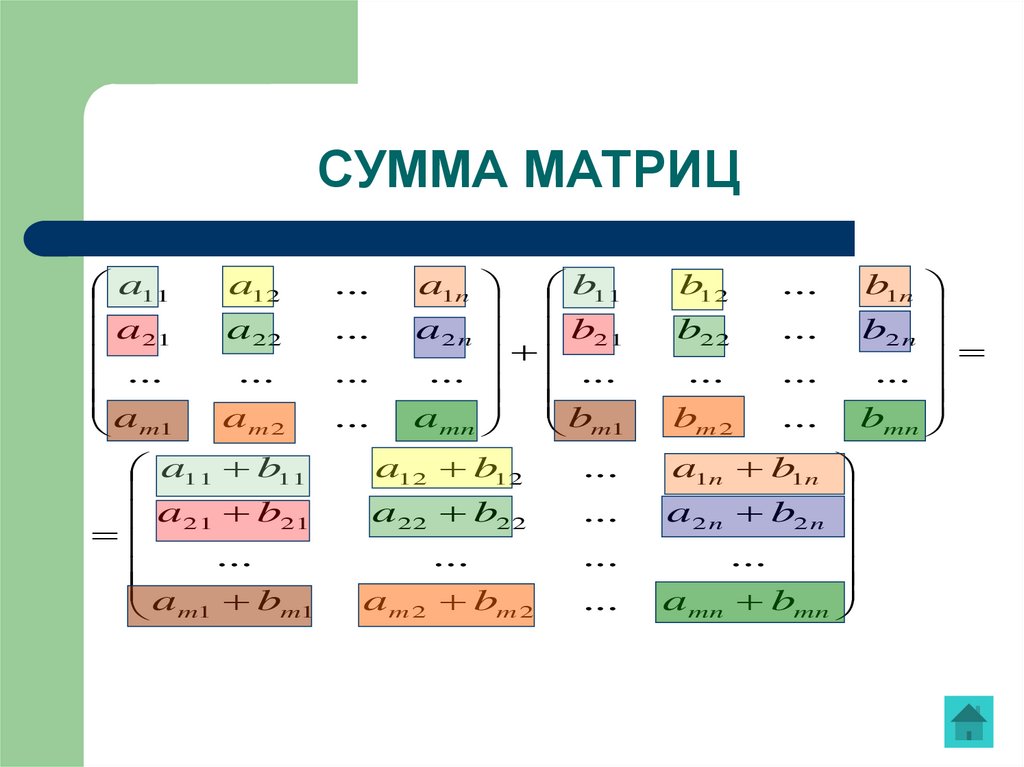
13. СУММА МАТРИЦ

матриц A=(aij) и
a11 a12 b11 b12 Суммой
B=(bij) одинаковой
размерностью mxn называется
a
a
b
b
21 22 21 22
матрица С=(cij) = A(aij)+B(bij)
a11 b11 a12 b12
a21 b21 a22 b22
тех же размеров , что и
заданные матрицы, элементы
которой определяются
правилом для всех cij=aij+bij,
для всех i=1, 2, … , m, и j=1, 2,
… , n.
Сумма матриц подчиняется переместительному и
сочетательному законам, т.е. А+В=В+А и
(А+В)+С=А+(В+С).

14. СУММА МАТРИЦ

a12
...
a1n b11
a11
a22
...
a2 n b21
a21
...
...
...
...
...
a
am 2
... amn
m1
bm1
a12 b12
...
a11 b11
a22 b22
...
a21 b21
...
...
...
a
am 2 bm 2
...
m1 bm1
b12
...
b22
...
...
...
bm 2
...
a1n b1n
a2 n b2 n
...
amn bmn
b1n
b2 n
...
bmn

15. Умножение матрицы на число

a11 a12 ... a1n
a21 a22 ... a2 n
k
...
... ... ...
a
a
...
a
m2
mn
m1
ka11 ka12 ... ka1n
ka21 ka22 ... ka2 n
...
...
...
...
ka
ka
...
ka
m2
mn
m1
Произведением
матрицы A=(aij)
размеров mxn на
число k называется
матрица B=(bij) тех же
размеров, что и
матрица А, элементы,
которой определяются
правилом bij=kaij, для
всех i=1, 2, … , m, и
j=1, 2, … , n.

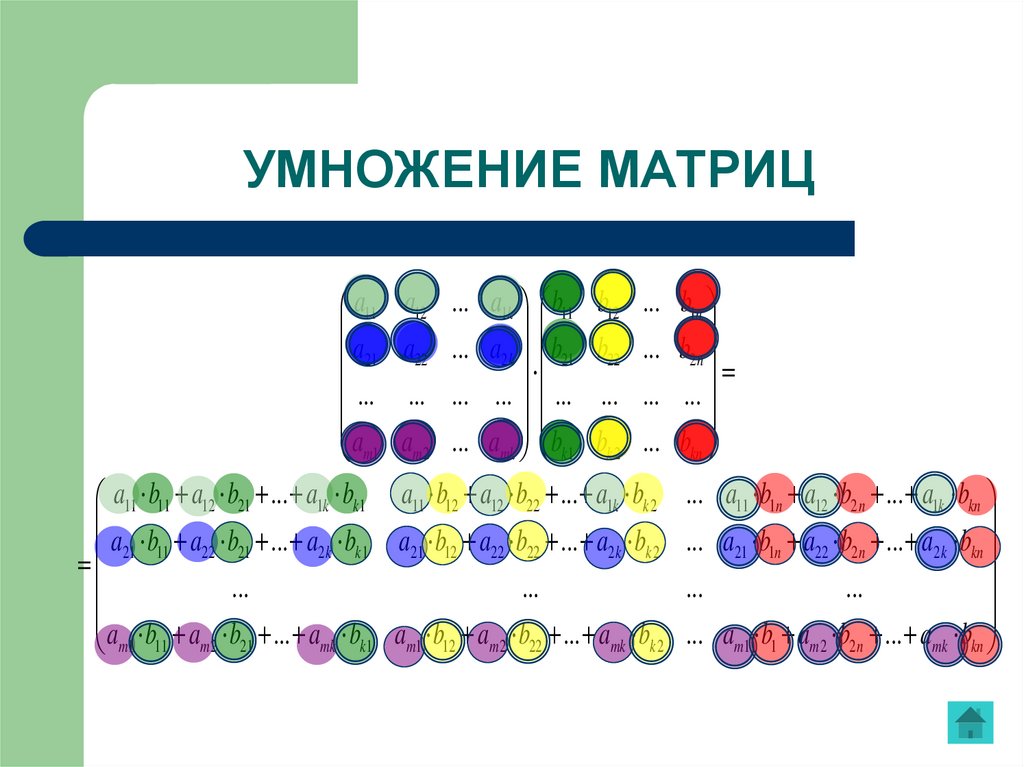
16. УМНОЖЕНИЕ МАТРИЦ

Пусть заданы матрица А размеров mxn и
матрица В размеров nxp, т.е. такие, что
число столбцов первой равно числу строк
второй матрицы. Выберем строку с
номером i из матрицы А и столбец с
номером j из матрицы В. Умножим каждый
элемент ai1, ai2, …, ain выбранной строки на
соответствующий элемент b1j, b2j, …, bnj
выбранного столбца и сложим полученные
произведения, т.е. составим сумму cij= ai1
b1j+ ai2 b2j+…+ ain bnj.

17. УМНОЖЕНИЕ МАТРИЦ

Произведением матрицы А размеров
mxn на матрицу В размеров nxp
называется матрица размеров mxp ,
элементы которой определяются по
формуле
cij= ai1 b1j+ ai2 b2j+…+ ain bnj
для всех i=1, 2, … , m, и j=1, 2, … , p.

18. УМНОЖЕНИЕ МАТРИЦ

a11 a12 ... a1k b11 b12 ... b1n
a
a
...
a
b
b
...
b
2 k 21
22
2n
21 22
... ... ... ... ... ... ... ...
am1 am 2 ... amk bk1 bk 2 ... bkn
a11 b11 a12 b21 ... a1k bk1 a11 b12 a12 b22 ... a1k bk 2 ... a11 b1n a12 b2 n ... a1k bkn
a
b
a
b
...
a
b
a
b
a
b
...
a
b
...
a
b
a
b
...
a
b
2 k k1
21 12
22 22
2k k 2
21 1n
22 2 n
2 k kn
21 11 22 21
...
...
...
...
am1 b11 am 2 b21 ... amk bk1 am1 b12 am 2 b22 ... amk bk 2 ... am1 b1 am 2 b2 n ... amk bkn

19. Определитель второго порядка

a11
A
a21
a11
a21
a12
a22
Определитель второго
порядка,
a12
соответствующий заданной
матрице A –
a22
a11 a22 a12 a21
число, равное
разности произведений
элементов, расположенных
на главной
и побочной его диагоналях.