Паралельність у просторі

1. Паралельність у просторі

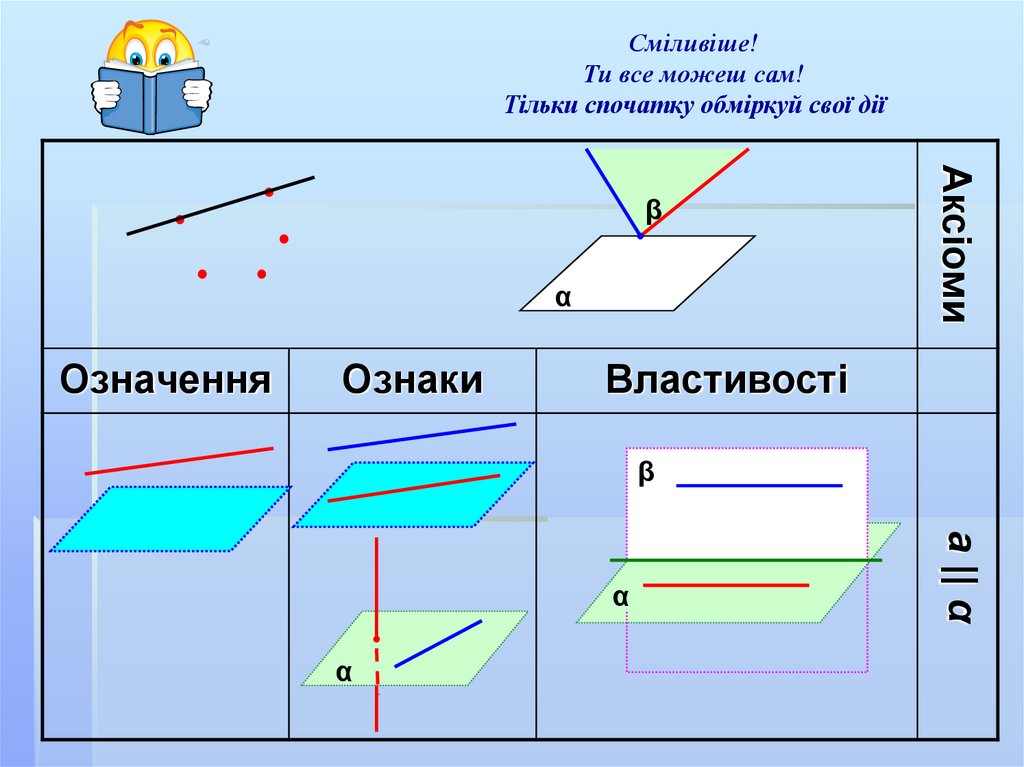
2. Сміливіше! Ти все можеш сам! Тільки спочатку обміркуй свої дії

α
Означення
Ознаки
Аксіоми
β
Властивості
β
α
а || α
α

3. Спробуй ще раз, у тебе обов'язково вийде

Означення Ознаки
Властивості
α
а
в
α ‫ ׀׀‬β
β

4. Завдання 1.13 (В 1)

а // в
а
а
в
в
α
а
в
с
β
180
а
а || с
в|| с
в
На малюнку зображено паралельні
прямі а і в та січна с. Чому дорівнює
сума кутів α і β?

5. Завдання 2

а // в
а
а
в
в
а
β
180
α
в
а
с
в
а || с
в|| с
Спостерігач, який стоїть на висоті 50 м бачить
автомобіль під кутом 30° до горизонту. Яка відстань
від спостерігача до автомобіля?

6. Завдання 1.15 (В 5)

α
А
D
В
С
Бічні сторони трапеції
паралельні площині α.
Яке взаємне розміщення
площини α і площини
трапеції ?.
α ‫ ׀׀‬β
α
β

7. Завдання 1.15 (В 9)

Дано:
ΔАВС.
Площина
паралельна
прямій
АС,
перетинає сторону AB у точці
М, а сторону ВС - точці N.
Яка довжина відрізка МN,
якщо точка М – середина АВ,
т.N – середина ВС, АС=16см?
B
M
N
α
а || α
A
C
α

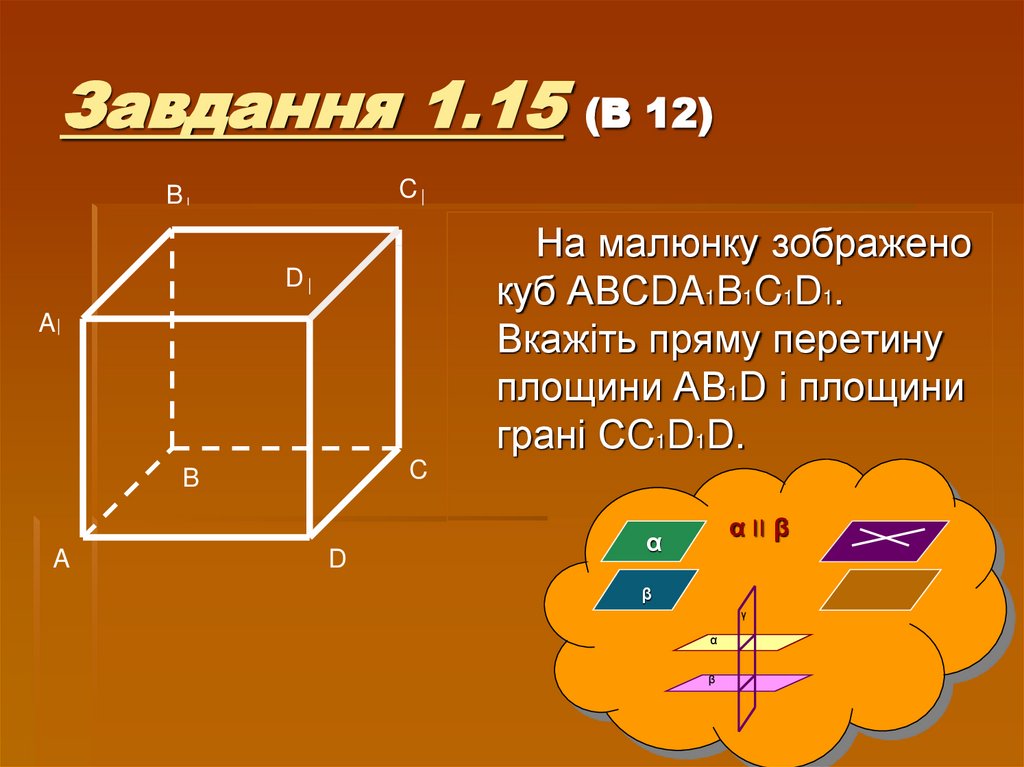
8. Завдання 1.15 (В 12)

C
B
На малюнку зображено
куб АВСDA1B1C1D1.
Вкажіть пряму перетину
площини АВ1D і площини
грані СC1D1D.
D
A
C
B
A
D
α ‫ ׀׀‬β
α
β
γ
α
β

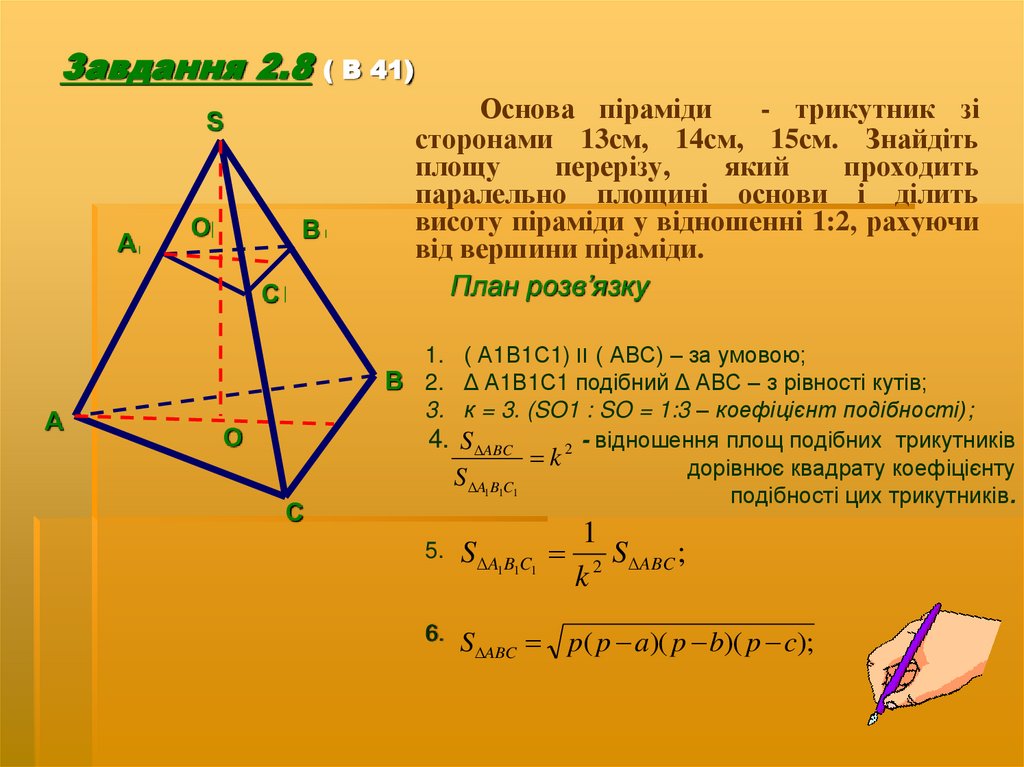
9. Завдання 2.8 ( В 41)

S
А
О
В
С
А
О
С
Основа піраміди
- трикутник зі
сторонами 13см, 14см, 15см. Знайдіть
площу
перерізу,
який
проходить
паралельно площині основи і ділить
висоту піраміди у відношенні 1:2, рахуючи
від вершини піраміди.
План розв’язку
1. ( А1В1С1) ‫ ( ׀׀‬АВС) – за умовою;
В 2. Δ А1В1С1 подібний Δ АВС – з рівності кутів;
3. к = 3. (SO1 : SO = 1:3 – коефіцієнт подібності);
4. S ABC
- відношення площ подібних трикутників
k2
дорівнює квадрату коефіцієнту
S A1B1C1
подібності цих трикутників.
5.
S A1B1C1
6. S
ABC
1
S ABC ;
2
k
p( p a)( p b)( p c);

10. Завдання 2.8 ( В 75)

Паралельно осі циліндра, радіус основи
якого дорівнює 6√2см проведено площину,
що перетинає основу циліндра по хорді,
яка стягує дугу, градусна міра якої
дорівнює 90º. Знайдіть площу перерізу,
якщо кут між діагоналлю перерізу і
вказаною хордою дорівнює 60º.
План розв’язку
1. ОО1 – відрізок вісі циліндра. (АВС) ‫ ׀׀‬ОО1 – за
умовою.
2. АВ‫׀׀‬ОО1; СD‫׀׀‬ОО1 АВСD – прямокутник;
3. АD –хорда, яка стягує AMD 90 AOD 90 AOD
- прямокутний.
4. АО = ОD = R = 6√2см.
D 90 ; CAD 60 ; DC AD tg60 .
5. ΔACD:
6. SABCD = AD • DC.