Корень n – ой степени

1. КОРЕНЬ n – ой СТЕПЕНИ

2. ОПРЕДЕЛЕНИЕ КОРНЯ n-й СТЕПЕНИ

Определение:
Корнем n –ой степени из числа «а»
называется такое число b, n –ая степень
которого равна «а», причем n называют
показателем корня, а-подкоренным
выражением.
Примечание:
если n –четное число, то а≥0;
если n –нечетное число, то а- любое.

3. ПРИМЕРЫ

4
81 3, т.к. 3 81
3
8 2 , т.к. 2 8
5
0 0 , т.к. 0 0
4
3
5
Примечание:
Принято корень второй степени называть
квадратным корнем, корень третьей степени –
кубическим корнем.

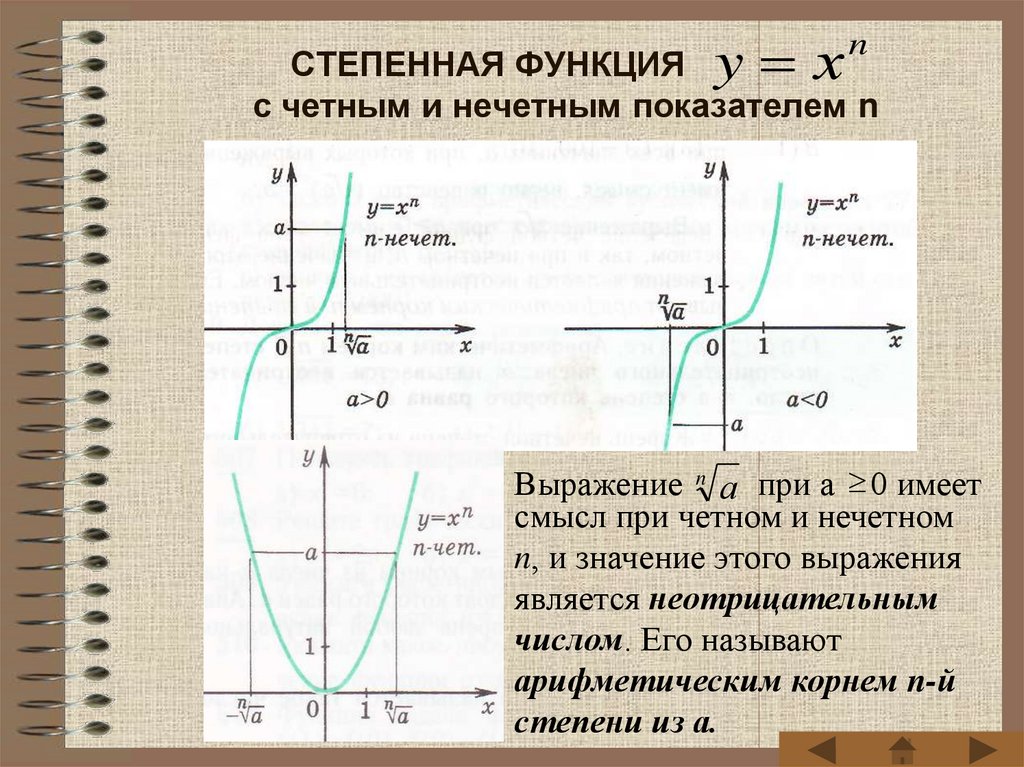
4. СТЕПЕННАЯ ФУНКЦИЯ с четным и нечетным показателем n

СТЕПЕННАЯ ФУНКЦИЯ y х
с четным и нечетным показателем n
n
Выражение n а при а 0 имеет
смысл при четном и нечетном
n, и значение этого выражения
является неотрицательным
числом. Его называют
арифметическим корнем n-й
степени из а.

5. ОПРЕДЕЛЕНИЕ АРИФМЕТИЧЕСКОГО КОРНЯ n-й СТЕПЕНИ

Определение:
Арифметическим корнем n-ой степени из
неотрицательного числа а называется
неотрицательное число, n-я степень которого равна а.
Примечание:
Корень нечетной степени из отрицательного числа
можно выразить через арифметический корень из
положительного числа.
Например:
3
64 3 64 ,т.к. 3 64 4 и 3 64 4

6. СВОЙСТВА КОРНЯ n-й СТЕПЕНИ

2)n a m (n a ) m
1)( n a ) n a
Например:
Например:
( 5) 5
8
8
4
28 (4 2 )8 (4 2 ) 4*2 ((4 2 ) 4 ) 2 2 2 4
3) n ab n a * n b
Например: 5 9 * 5 27 5 9 * 27 5 3 2 * 33
n
a
a
n
4)
n
b
b
Например:
2
4
2
64
2
4 2 1 1
64
16 4
5)2 m a 2 m a
Например:
6
( 5) 6 5 5
5 35 3

7. ЗАДАНИЯ

Используя приведенные свойства, вычислить:
7
7
5 10
а )( 3 )
б) 3
в) 4 * 8
5
5
д ) ( 7 )
6
ж)
3
6
31 2 * 2 31
3
3
г) 3
4
108
10
е) 3 2
27

8. ПРОВЕРКА

а )( 3 ) 3
7
7

9. ПРОВЕРКА

б) 3 ( 3) ( 3) (( 3) ) 3 9
5 10
5
10
5
5*2
5
5 2
2

10. ПРОВЕРКА

в) 4 * 8 4 * 8 2 * 2 2 2
5
5
5
5
2
3
5
5

11. ПРОВЕРКА

3
4
4
1
1
г) 3
3
3
108
27 3
108

12. ПРОВЕРКА

д) ( 7) 7 7
6
6

13. ПРОВЕРКА

3
10
64
64
4
е) 3 2
3
3
27
27
27 3

14. ПРОВЕРКА

ж)3 31 2 * 3 2 31 3 ( 31 2)(2 31) 3 ( 31 2)( 31 2) 3 ( 31) 2 22 3 31 4 3 27 3