Корень n-ной степени

1.

Корень n-ой степени
n
а

2. Понятие корня n-ой степени

Корнем n-ой степени из неотрицательного
числа а (n = 2, 3, 4, 5, ...) называют такое
неотрицательное число, при возведении
которого в степень п получается число а.
n
a b, b n a , где a 0 , b 0 , n N , n 1
Число а называют подкоренным числом,
а число n – показателем корня

3. Примеры

1)
3
2)
4
3)
5
27 3;
33 27
256 4;
44 256
0,00243 0,3;
0,35 0,00243
100 3 1000000
4)
3
1000000 100 ;
5)
3
64000 40 ;
6)
6
1
1
;
64 2
40 3 64000
6
1
1
64
2

4. Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
1
n
1)
4
2)
3
4)
n
где a 0, b 0
b,
16 625 4 16 4 625 2 5 10;
2
3)
ab n a
4 3 16 3 4 16 3 64 4;
n
a na
n ,
b
b
где a 0, b 0
19 5 243
5 7
32
32
6
243 3
1,5;
5
2
32
5
256 6 256 6
64 2;
6
4
4

5. Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
a
3
5)
6)
k
n
4
2
3
5
4
n
3 42 3 16;
81 3
5
n k
где a 0
ak ,
4
3 ;
5
4
a nk a ,
где a 0
7)
3
729 6 729 3;
8)
3 5
а15 15 а15 а;

6. Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
5
9)
np
12
где a 0
a9 4 a3 ;
с 3 с 6 с3 6 с2 6 с3 с2 6 с5 ;
10)
6
a kp n a k ,
n
a , n четно
a
a , n нечетно
n
( 3,25)8 3,25 3,25;
11)
8
12)
11
т11 т;

7. Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
7
n
a n a , n нечетно
13)
7
128 7 128 2;
14)
8
3
0,000125 3 0,000125 0,05;
k
n
a n ak ,
см. далее
где a 0

8.

n
y
x
Функции вида
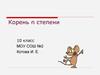
Свойства функции y n x , n – чётное число
1.
2.
3.
4.
5.
6.
7.
8.
9.
D(у) = [0; + ).
E(у) = [0; + ).
Функция ни чётная, ни нечётная.
а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
[0; + ) – промежуток возрастания функции;
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве [0; + ).
Выпукла вверх.

9.

n
y
x,
Функции вида
n = 2k – чётное число
y
y 2k x
1
0
1
x

10.

n
y
x
Функции вида
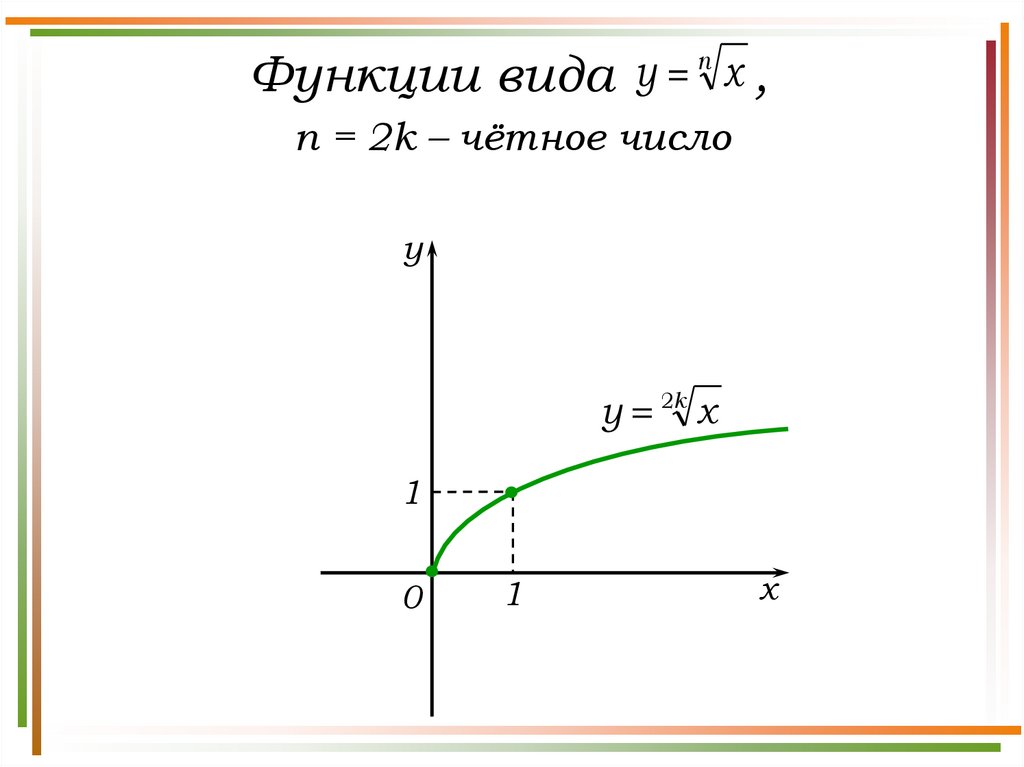
Свойства функции y n x , n – нечётное число
1. D(у) = (- ; + ).
2. E(у) = (- ; + ).
3. Функция нечётная.
4. а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
5. (- ; + ) – промежуток возрастания функции;
6. Не ограничена снизу, не ограничена сверху.
7. а) унаим. – не существует;
б) унаиб. – не существует.
8. Непрерывна на множестве (- ; + ).

11.

n
y
x,
Функции вида
n = 2k + 1 – нечётное число
y
y 2k 1 x
1
-1
1
0
-1
x

12. Вычисление производной

1 n1 1 1 1 nn 1 n 1 n
1
x x x
x
x
n 1
n
n
n
n
n x
n
1
n
k
k n
1
k n
k n
k n k n
k
k
x x x x
x
n k
n
n
n
n
n
x
n
k
n
kn
k
1 n
n
kx b
kx b kx b
n 1
n
n n kx b
1
n

13. Вычисление производной

Примеры
1)
2)
3)
4)
35
35
1
6
6 7x 4
7x 4 6
6
6 7x 4
3
7
4
1 3 2
1
x
x
3
33 x2
2 7 5
2
2
x
x
7
7 7 x5
54
5
3
5x 7
5x 7
3
4
4 4 5x 7
5

14. Формула сложного радикала

a a2 b
a a2 b
a b
2
2
Примеры

15.

МБОУ СОШ №5 – «Школа здоровья и развития» г. Радужный
Степень с рациональным
показателем
a
r
Учитель математики Е.Ю. Семёнова

16. Понятие степени с рациональным показателем

p
q
q
a a , где a 0, q N, q 1, p Z
p
Примеры
1)
2)
3)
2
3
5 3 5 2 3 25
7
5
121,4 12 5 127
4
9
2
2
5
4
9
12
5
4
9
5
12
12
9
4
5

17. Свойства степени с рациональным показателем (для n ∈ Q, k ∈ Q)

1
a 0 1,
2
a1 a
3
a 1
4
a n
5
где a 0
6
1
, где a 0
a
1
n , где a 0
a
10
a
b
где a 0
7
a
8
a n b n ab
9
an a
,
n
b
b
n k
a nk
n
n
a n a k a n k
n
an
n k
a
,
k
a
n
b
,
a
где a 0 , b 0
где b 0

18.

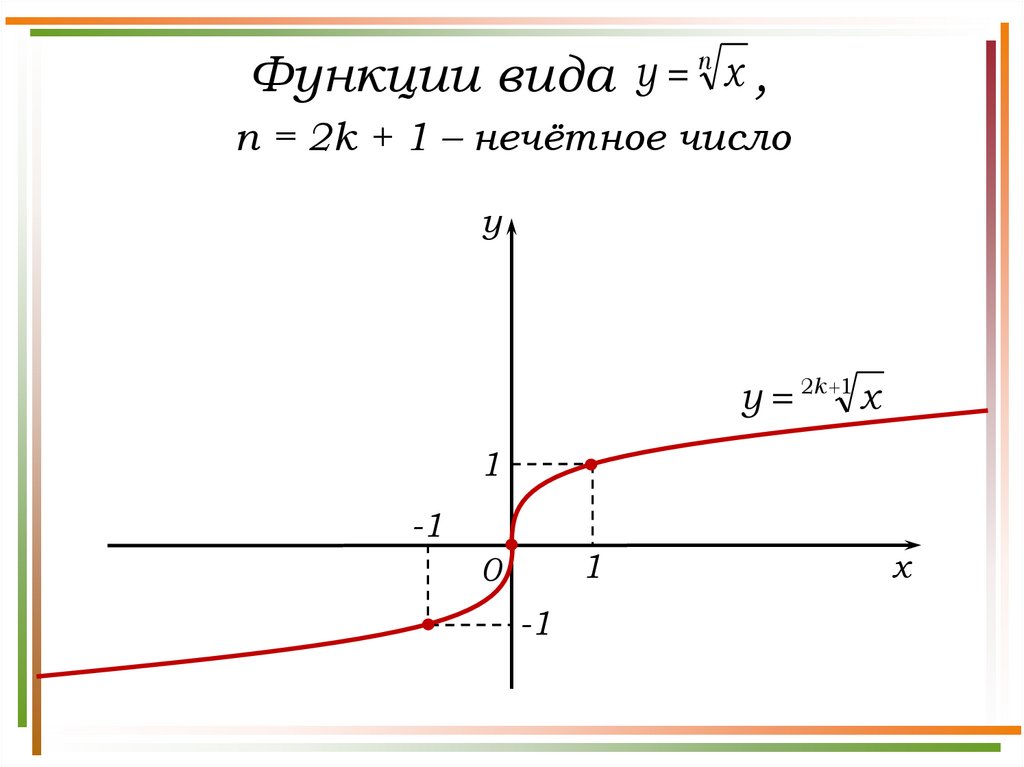
Степенные функции y = x r
Свойства функции y = x r, r Q, r > 1
1.
2.
3.
4.
5.
6.
7.
8.
9.
D(у) = [0; + ).
E(у) = [0; + ).
Функция ни четная, ни нечетная.
а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
[0; + ) – промежуток возрастания функции;
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве [0; + ).
Выпукла вниз.

19.

Степенные функции y = x r
График функции y = x r, r Q, r > 1
y
y = x r, r > 1
1
0
1
x

20.

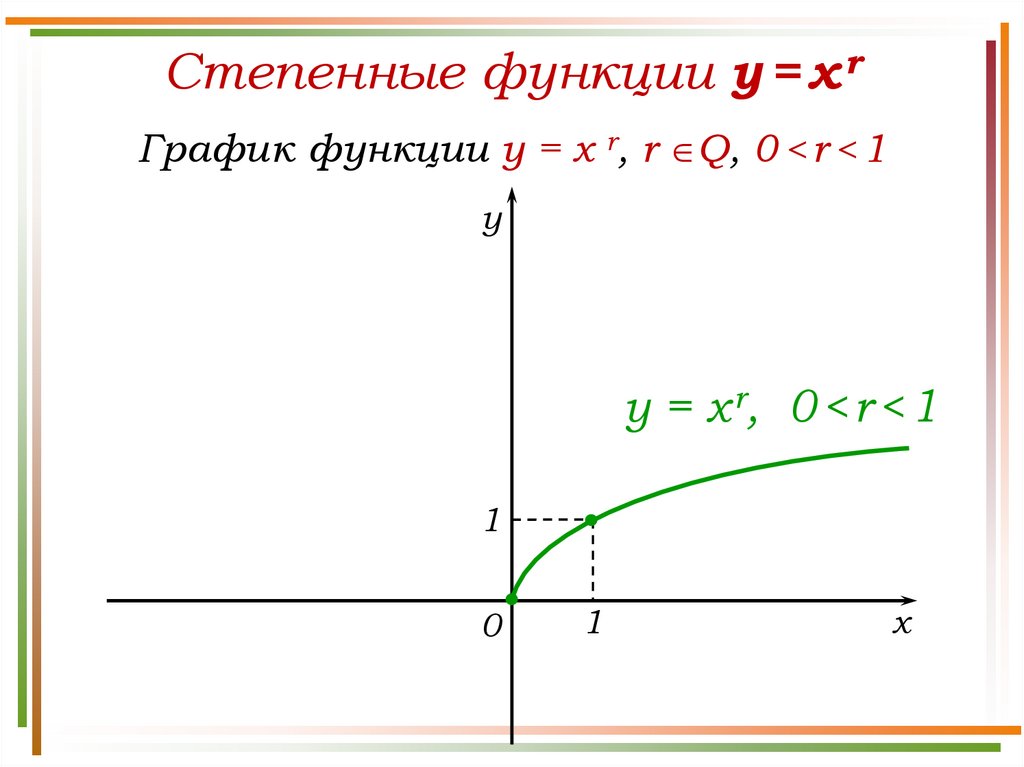
Степенные функции y = x r
Свойства функции y = x r, r Q, 0 < r < 1
1.
2.
3.
4.
5.
6.
7.
8.
9.
D(у) = [0; + ).
E(у) = [0; + ).
Функция ни четная, ни нечетная.
а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
[0; + ) – промежуток возрастания функции;
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве [0; + ).
Выпукла вверх.

21.

Степенные функции y = x r
График функции y = x r, r Q, 0 < r < 1
y
y = x r, 0 < r < 1
1
0
1
x

22.

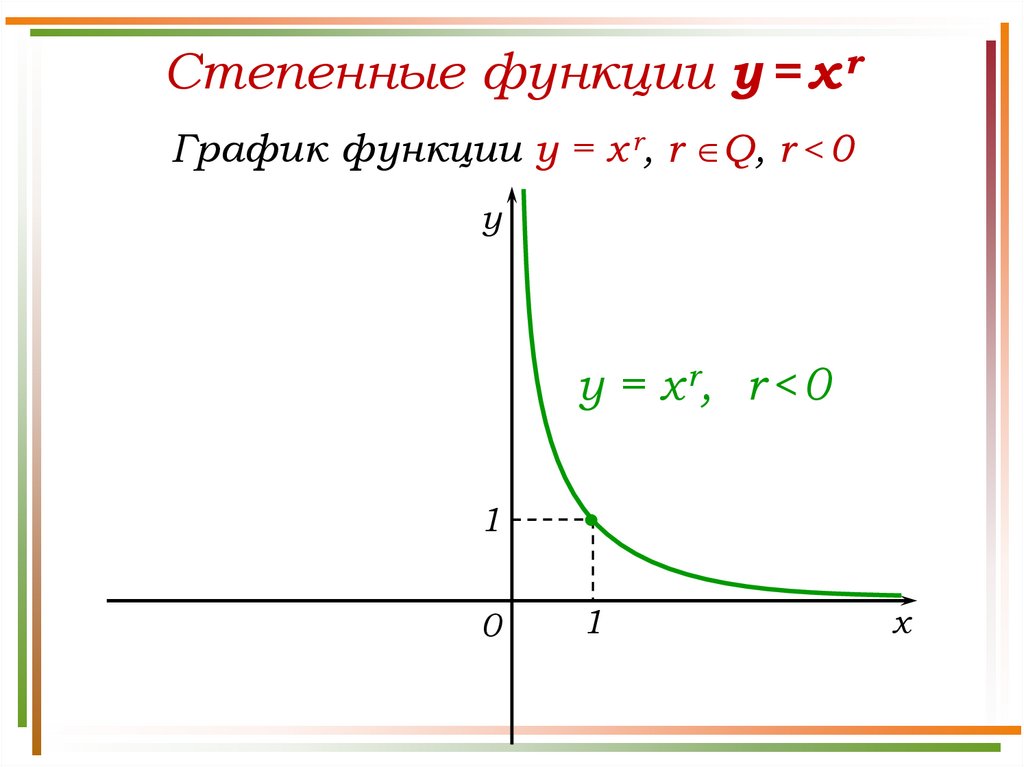
Степенные функции y = x r
Свойства функции y = x r, r Q, r < 0
1.
2.
3.
4.
5.
6.
7.
8.
9.
D(у) = (0; + ).
E(у) = (0; + ).
Функция ни четная, ни нечетная.
а) Нули функции: нет.
б) Точка пересечения с Оу: нет.
(0; + ) – промежуток убывания функции;
Ограничена снизу, не ограничена сверху.
а) унаим. – не существует;
б) унаиб. – не существует.
Непрерывна на множестве [0; + ).
Выпукла вниз.

23.

Степенные функции y = x r
График функции y = x r, r Q, r < 0
y
y = x r, r < 0
1
0
1
x

24.

Задания открытого банка задач
1. Найдите значение выражения
652 562.
Решение.
652 562 (65 56)(65 56) 9 121 3 11 33.
2 7 .
2
2. Найдите значение выражения
Решение.
2 7
2
14
14
4 7 28
2.
14
14
3. Найдите значение выражения
Решение.
13 7 13 7
2
2
13 7 13 7 .
13 7 13 7 6.

25.

Задания открытого банка задач
4. Найдите значение выражения 50,36 250,32 .
Решение.
50,36 250,32 50,36 52
0,32
50,36 50,64 50,36 0,64 51 5.
36,5
5. Найдите значение выражения 2,25 .
9
Решение.
36,5
36,5
36,5
6,5 4,5
2
3
3
9.
2,25
2,25
4,5
2
9
3
3
4
9
5
18
6. Найдите значение выражения 7 49 .
Решение.
4
9
5
18
7 49
4
9
5
2 18
7 7
4
9
5
9
7 7 7
4 5
9 9
9
9
7 71 7.

26.

Задания открытого банка задач
23,5 35,5
7. Найдите значение выражения
.
64,5
Решение.
23,5 35,5 23,5 35,5 23,5 35,5
3
3,5 4,5
5,5 4,5
1
1
2
3
2
3
1,5.
4,5
4,5
4,5
4,5
6
2 3
2
2 3
8. Найдите значение выражения 35 4,7 75,7 : 5 3,7 .
Решение.
35 4,7 75,7 : 5 3,7 5 7
4,7
5 4,7 3,7 7 4,7 5,7
75,7 53,7 5 4,7 7 4,7 75,7 53,7
7
5 1 71 1,4.
5
2,8 4,2
9. Найдите значение выражения
Решение.
2,8 4,2
2,8 4,2
28 42
49 7.
0
,
24
24
0,24
0,24
.

27.

Задания открытого банка задач
10. Найдите значение выражения
Решение.
6
5
3
3 1 :
.
7
7
28
27
27
6
5
3
12
3
12 28
3 1 :
:
7
7 28 7
7 28 7
7
3
27 28
12 28
27 28
12 28
9 4 4 4 6 4 2.
7
3
7
3
7 3
7 3
11. Найдите значение выражения
Решение.
9
9
7 18 7
.
6
7
7 18 7 18 72 18 7 18 72 7 18 73 18
1 1.
3
3
6
18 3
7
7
7
7

28.

Задания открытого банка задач
12. Найдите значение выражения
Решение.
5
5
10 5 16
.
5
5
10 5 16 5 10 16 5
32 2.
5
5
5
13. Найдите значение выражения
Решение.
2 2
12
2
1
3
1
4
2
2 2
1
212
1
3
1
4
2
13 14
2 2
12
2
2
.
1 1 1 2
4 3 1 2
1 2
3 4 12
12
2
2
2
2 2.

29. Использованы ресурсы

• Алгебра и начала математического анализа. 11 класс. В 2 ч.
Ч. 1. Учебник для учащихся общеобразовательных
учреждений (профильный уровень) / А.Г. Мордкович, П.В.
Семенов. – 2-е изд., стер. – М.: Мнемозина, 2008.
• http://mathege.ru/or/ege/Main.html - открытый банк заданий
ЕГЭ по математике (профильный уровень)