Методы описания дискретных систем

1. Методы описания дискретных систем

Основы системного анализа
Методы описания дискретных систем

2. Описание дискретных систем в частотной области

1. Описание непрерывных систем
u t U p
u t U
d x t
d y t
y t ak
bm
k
m
dt
dt
k 0
m 1
k
K
K
M
m
M
Y p ak X p p bmY p p
k
k 1
m
(1)
m 1
K
Y p
H p
X p
H p
k
a
p
k
m k
k 1
M
1 bm p
m 1
(2)
m
2

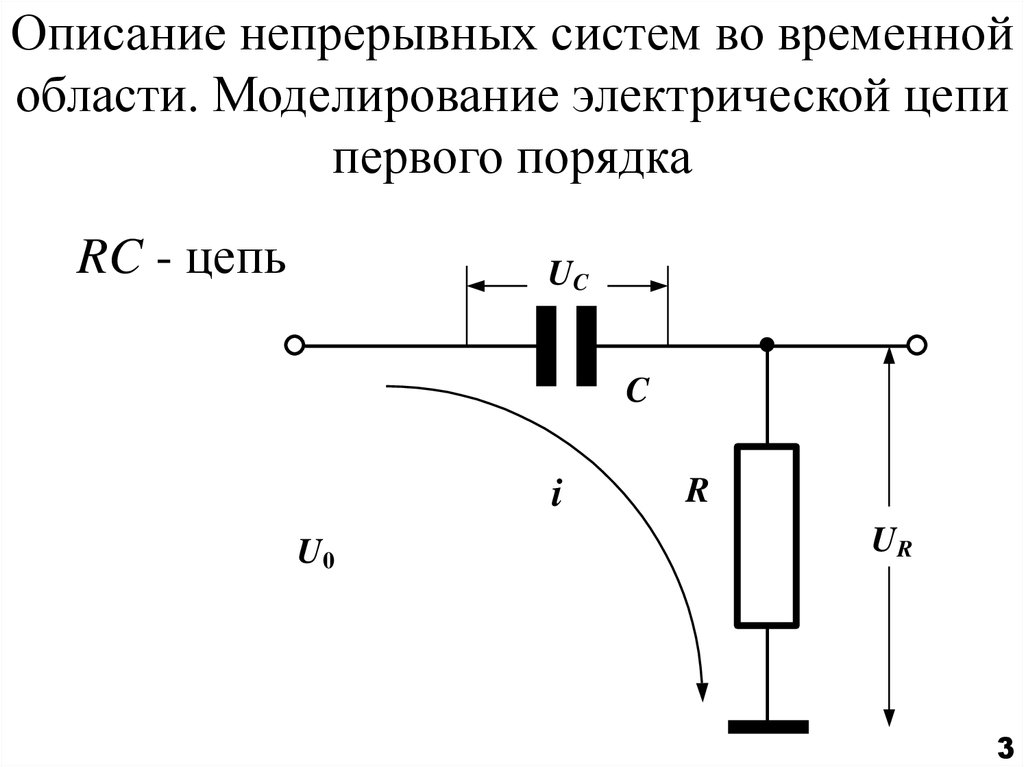
3. Описание непрерывных систем во временной области. Моделирование электрической цепи первого порядка

RC - цепь
UC
C
i
U0
R
UR
3

4. Уравнения электрической цепи первого порядка

Уравнения цепи
i t iR t iC t
(1)
duC t
iC t C
dt
(2)
duC t
uR t i t R iC t R RC
dt
uR t uC t U 0 t
duC t
RC
uC t U 0 t
dt
(3)
(4)
(5)
4

5. Решение уравнения электрической цепи первого порядка

Уравнение (5) является неоднородным линейным уравнением первого порядка.
Общее решение неоднородного уравнения представляется как сумма какогонибудь частного решения этого уравнения и общего решения соответствующего
однородного уравнения
duC t
RC
uC t 0 (6), т.е.
dt
uC î áù uC ÷àñòí uC î äí
(7)
Общее решение уравнения (6)
duC t
RC
uC t (8)
dt
t
ln uC t
ln A1
RC
(9)
где A1 - произвольная постоянная интегрирования.
Окончательное решение
t
RC
uC t U 0 1 e
(10)
5

6. Дискретизация уравнения цепи первого порядка для моделирования на ЭВМ

Замена производной конечной разностью:
duC t
dt
uC t uC t t
t
(11)
Замена непрерывного времени дискретным: t n
uC n uC n t
RC
uC n U 0 n
t
(12)
6

7. Дискретизация уравнения цепи первого порядка для моделирования на ЭВМ

Преобразуем уравнение (12):
uC n uC n t
1
1
uC n
U 0 n ;
t
RC
RC
t
t
uC n uC n t
uC n
U 0 n ;
RC
RC
t t
uC n 1
U 0 n uC n t ;
RC RC
k t
1
uC n
U 0 n kuC n t ,
ãäå k
RC
1 t
RC
RC
.
t RC
7

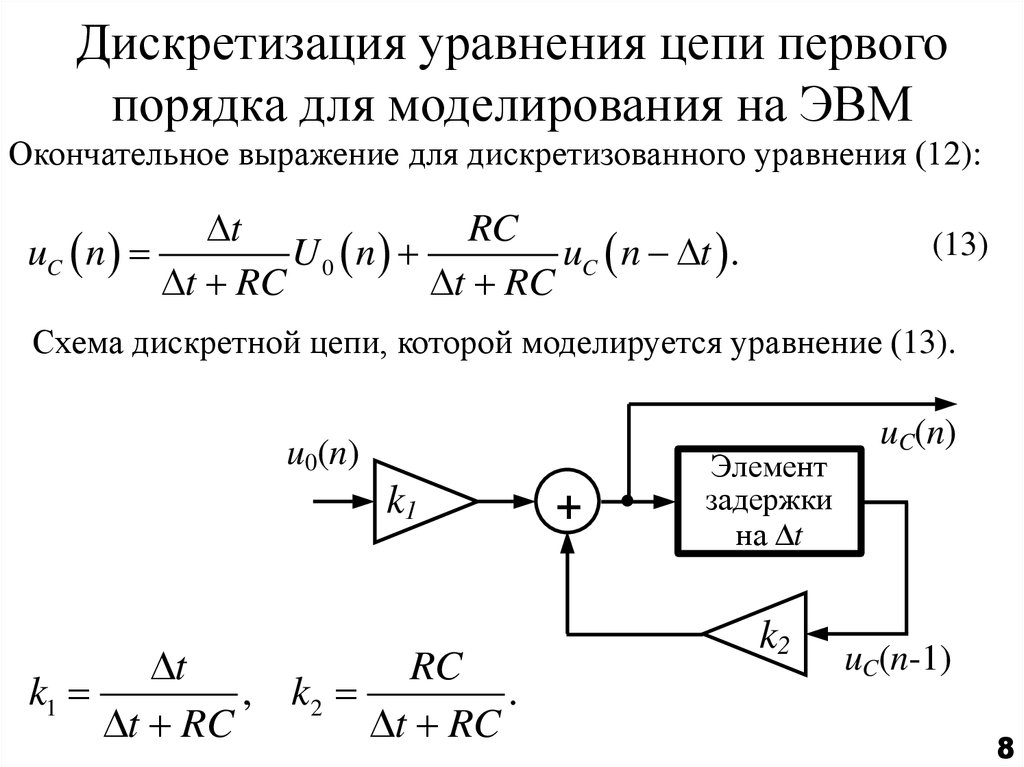
8. Дискретизация уравнения цепи первого порядка для моделирования на ЭВМ

Окончательное выражение для дискретизованного уравнения (12):
t
RC
uC n
U0 n
uC n t .
t RC
t RC
(13)
Схема дискретной цепи, которой моделируется уравнение (13).
u0(n)
k1
t
RC
k1
, k2
.
t RC
t RC
+
Элемент
задержки
на t
k2
uC(n)
uC(n-1)
8

9. Описание дискретных систем в частотной области

2. Изображение преобразования Лапласа функции
e t cos t
9

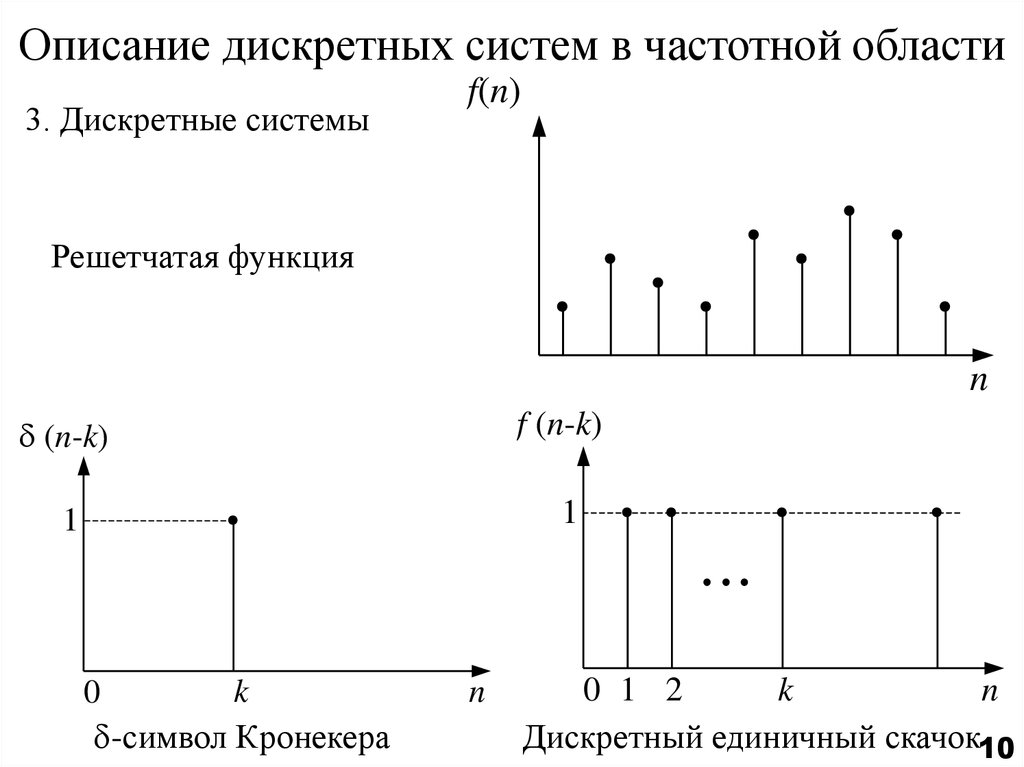
10. Описание дискретных систем в частотной области

3. Дискретные системы
f(n)
Решетчатая функция
n
f (n-k)
(n-k)
1
1
k
0
-символ Кронекера
n
k
n
0 1 2
Дискретный единичный скачок10

11. Описание дискретных систем в частотной области

f t t nT
4. Последовательность -функций
n 0
(n-k)
0 1 2
k
d
n
Дискретное преобразование Фурье последовательности -функций
1 N 1
Y k y n exp j 2 k N , k 0,1,2,
N n 0
, N 1 (14)
11

12. Описание дискретных систем в частотной области

5. Дискретное преобразование Лапласа
t : L t
t e
pt
dt 1 L t nTd e
pnTd
L y nTd Yd p y kTd e pkTd
k 0
Тогда
L y nTd Yd p y kTd e
pkTd
(15)
k 0
L f n kTd F p f n k p
k 0
k
(15а)
12

13. Описание дискретных систем в частотной области

6. Пример
f t exp t , 0
f d nTd Kr 0 e Td Kr t Td e 2Td Kr t 2Td
e mTd Kr t mTd
Тогда, с учетом (15)
Yd p 1 e Td e pTd e 2Td e 2 pTd
e mTd e mpTd
(16)
Выражения (15) и (16) громоздки (двойные суммы
трансцендентных функций) и неудобны для использования
13

14. Описание дискретных систем в частотной области

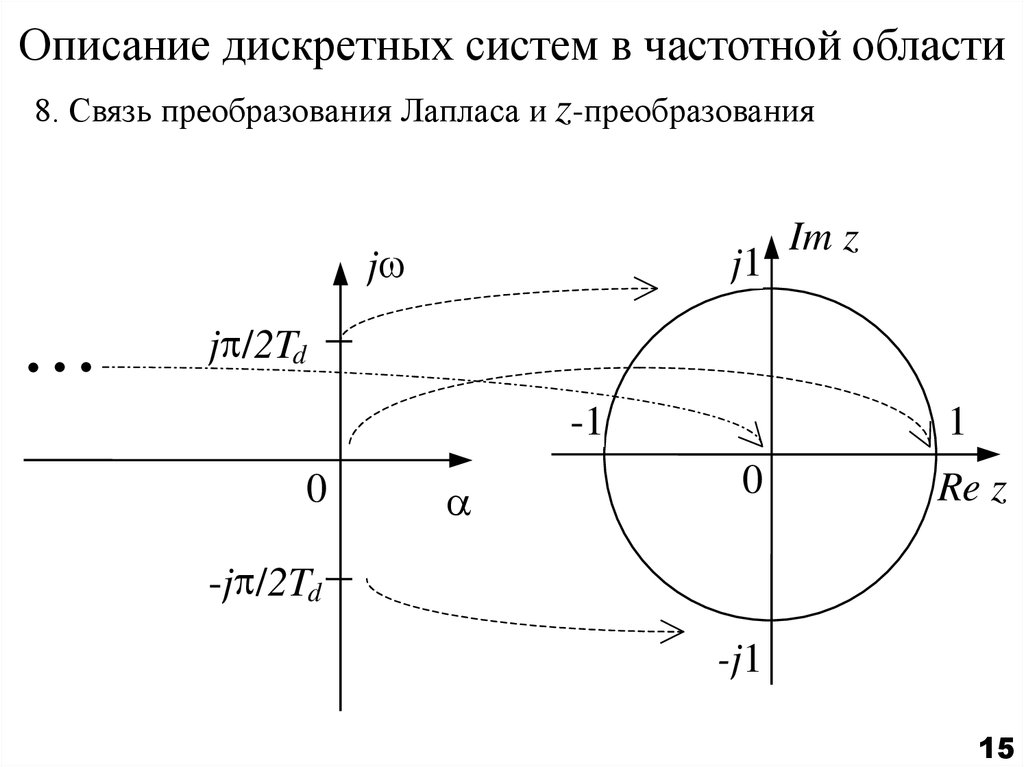
z e
7. z-преобразование
pTd
e
j Td
Тогда выражение (5) преобразуется к виду
Y z 1 e Td z 1 e 2Td z 2
e mTd z m
, (17)
а это– геометрическая прогрессия со знаменателем q e Td
z
1
При q 1 Y z
Td
z e
1 e Td z 1
Полюс функции (18)
(18)
z p exp Td
K
K
M
k 0
m 1
y n ak x n k bm y n m
Y z
H z
X z
k
a
z
k
k 0
M
1 bm z m
(19)
m 1
14

15. Описание дискретных систем в частотной области

8. Связь преобразования Лапласа и z-преобразования
j
j1
Im z
j /2Td
-1
0
1
0
Re z
-j /2Td
-j1
15

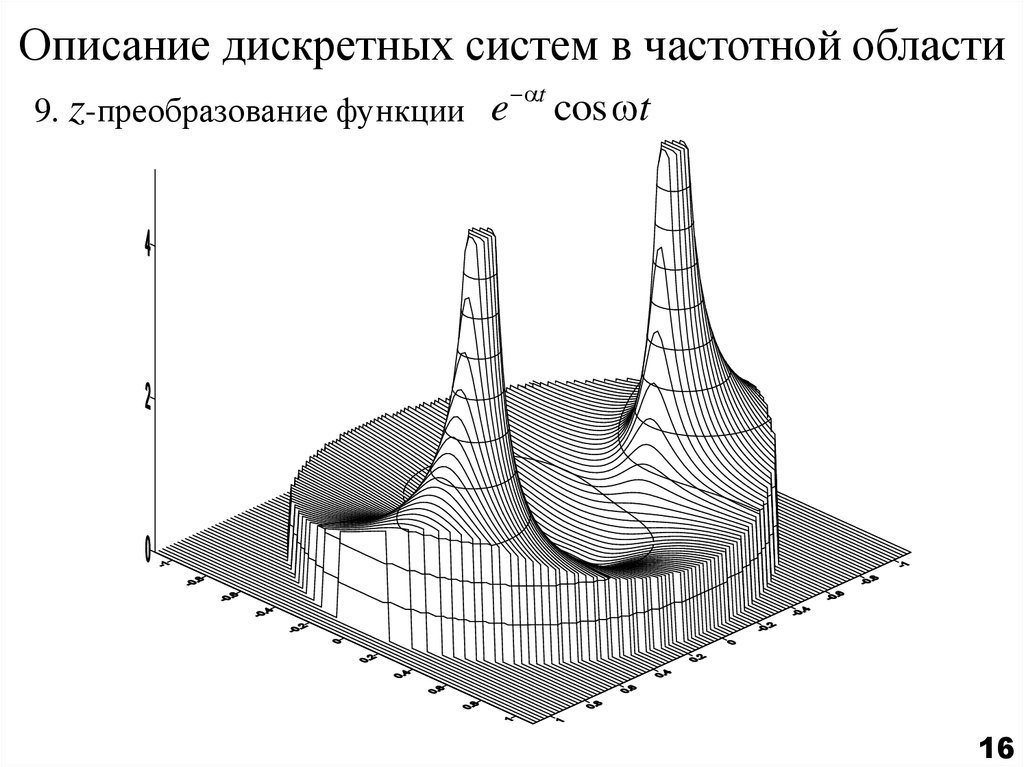
16. Описание дискретных систем в частотной области

9. z-преобразование функции e
t
cos t
16

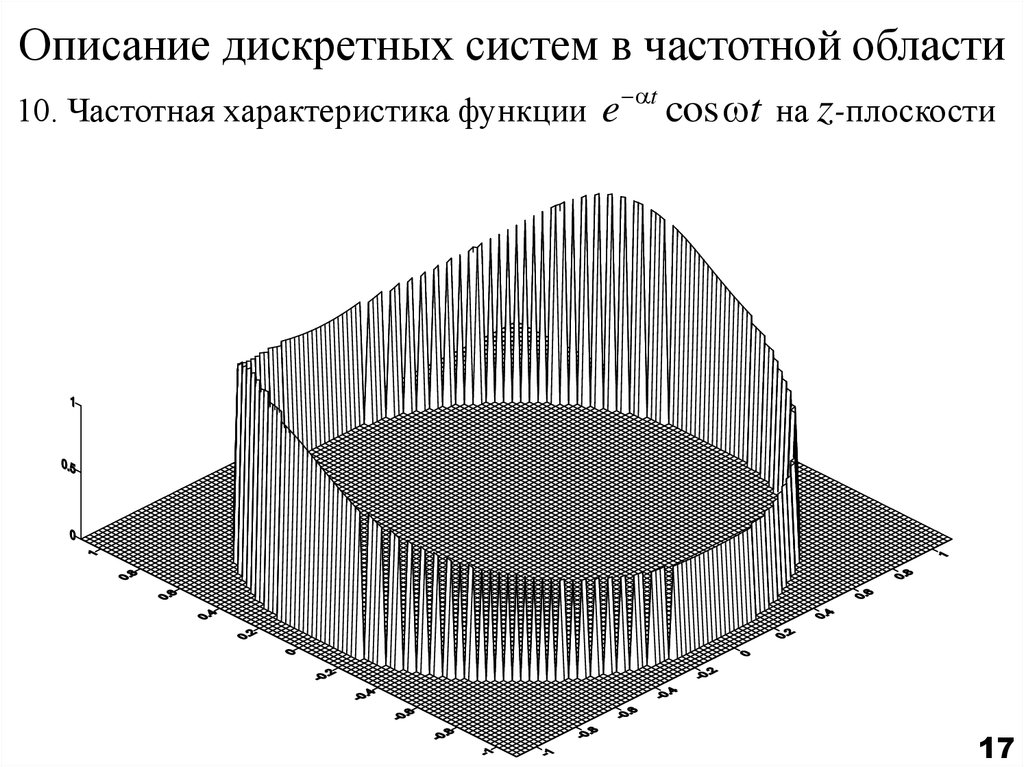
17. Описание дискретных систем в частотной области

10. Частотная характеристика функции e
t
cos t на z-плоскости
17

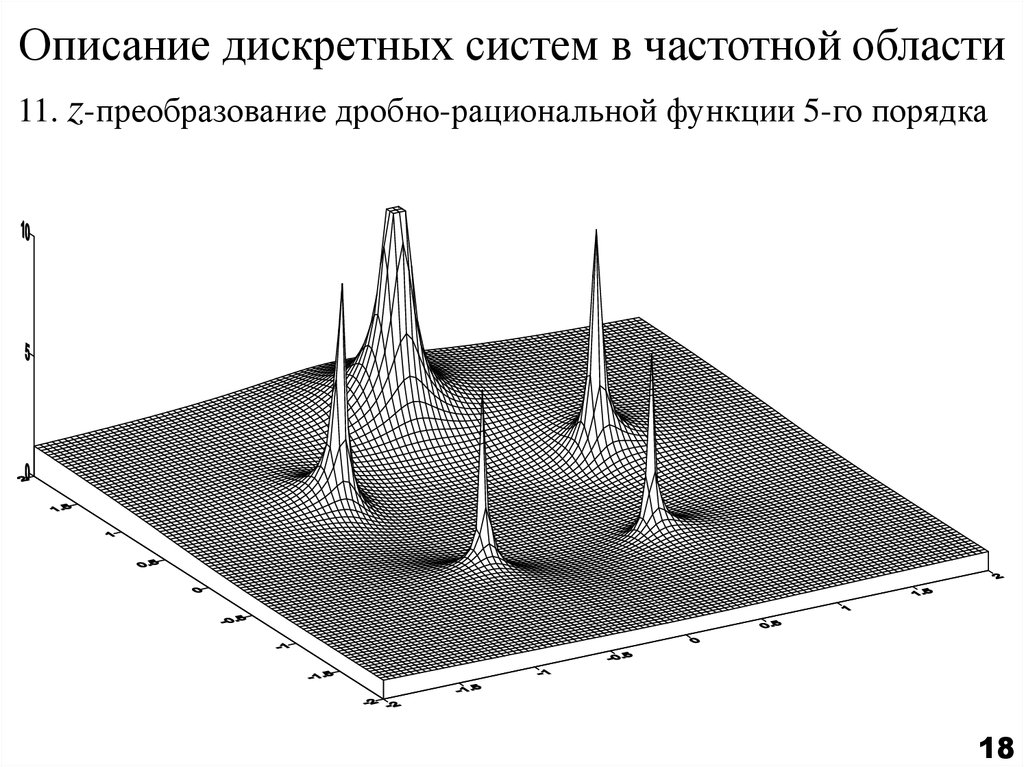
18. Описание дискретных систем в частотной области

11. z-преобразование дробно-рациональной функции 5-го порядка
18

19. Описание дискретных систем в частотной области

12. z-преобразование дробно-рациональной функции 5-го порядка
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
19

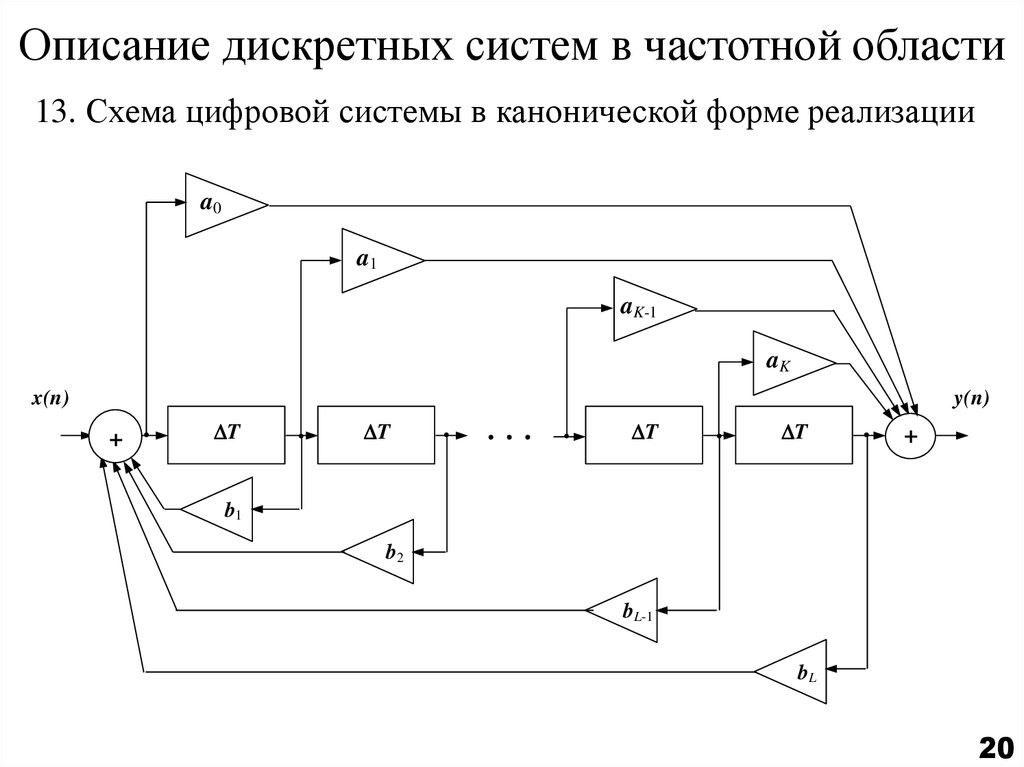
20. Описание дискретных систем в частотной области

13. Схема цифровой системы в канонической форме реализации
a0
a1
aK-1
aK
x(n)
y(n)
++
T
T
T
T
+
b1
b2
bL-1
bL
20

21. Описание дискретных систем в частотной области

14. Схемные реализации дискретных систем
Последовательная
H z
1
K
k
b
z
k
k 0
1
1
z
zk
K
k 1
21

22. Описание дискретных систем в частотной области

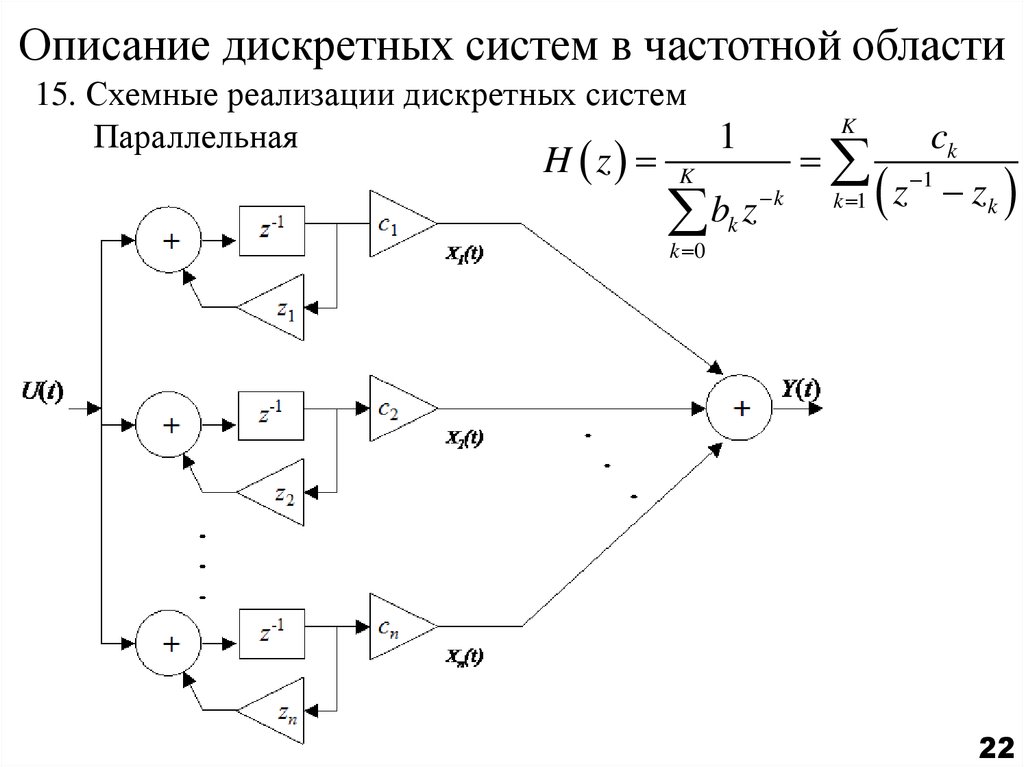
15. Схемные реализации дискретных систем
Параллельная
1
H z
K
k
b
z
k
K
ck
1
zk
k 1 z
k 0
22

23. Применение метода пространства состояний для описания сложных систем

Определим состояние системы как минимальное количество информации
относительно воздействий предыдущих сигналов на входе системы, необходимое
для полного описания выходного сигнала на некотором интервале наблюдения .
Переменные величины, которые содержат эту информацию, называются
переменными состояния.
Рассмотрим общий метод описания сложной динамической системы в терминах
переменных состояния. Пусть система описывается дифференциальным
уравнением вида:
y ( n ) (t ) Pn 1 (t ) y ( n 1) (t )
где
P0 (t ) y(t ) b0 (t )è (t )
(20)
(n)
d
y (t )
y ( n ) (t )
– n-я производная от y (t ) ; Pn (t ) – коэффициенты,
n
dt
зависящие от времени; b0 (t ) – зависящий от времени коэффициент усиления
входного сигнала U(t).
23

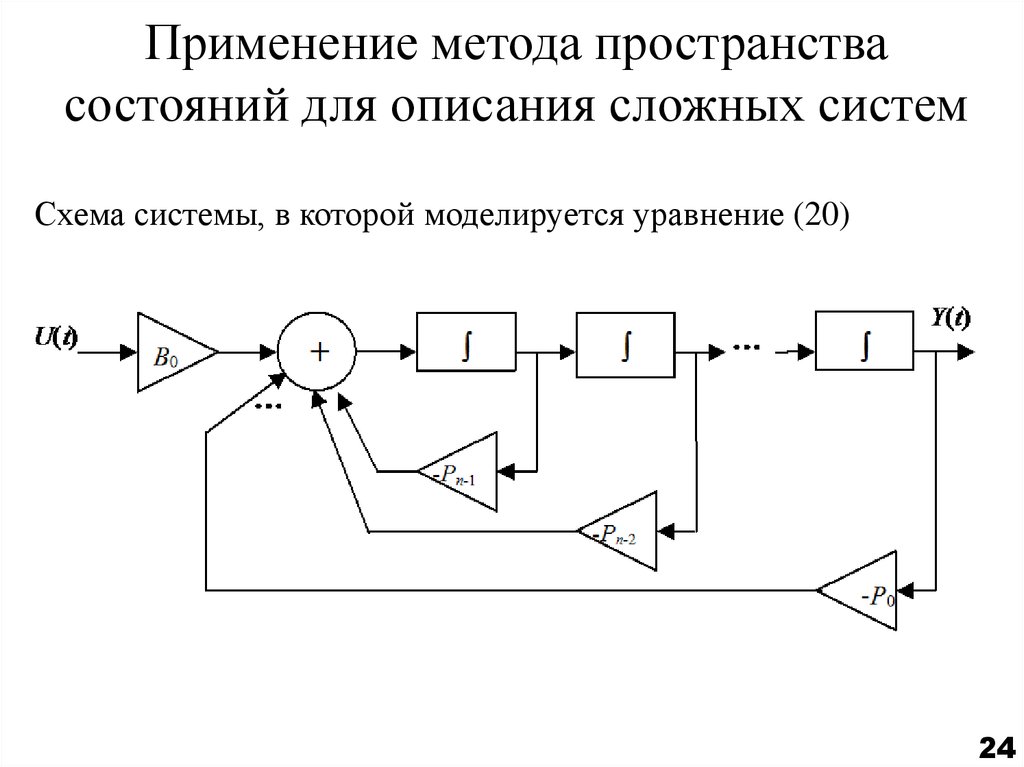
24. Применение метода пространства состояний для описания сложных систем

Схема системы, в которой моделируется уравнение (20)
24

25. Применение метода пространства состояний для описания сложных систем

Векторное представление уравнения (20)
X 1 (t ) Y (t )
X 2 (t ) Y (t ) X 1(t )
X 3 (t ) Y (t ) X 1 (t )
X n (t ) Y ( n 1) (t ) X n 1 (t )
(20а)
или
X n (t ) Y (t ) Pk 1 (t )Y
n
n
(n)
k 1
( k 1)
(t ) B0 (t )U (t ) Pk 1 (t ) X k (t ) B0 (t )U (t )
k 1
(20б)
25

26. Применение метода пространства состояний для описания сложных систем

Представим набор переменных X (t ), X (t ), , X (t ) в виде
1
2
n
вектор-столбца X (t ). Тогда скалярному уравнению (20) n-го
порядка соответствует n-мерное векторное уравнение первого
порядка
где
dx (t )
X(t ) F(t ) X(t ) G (t )U(t ),
dt
1
0
0
0
0
1
F
0
0
0
P P P
1
2
0
0
1
Pn 1
(21)
0
0
Y(t ) CX(t )
G
0
B0
C 1
0
0
0
26