Тетраэдр параллелепипед

1.

2.

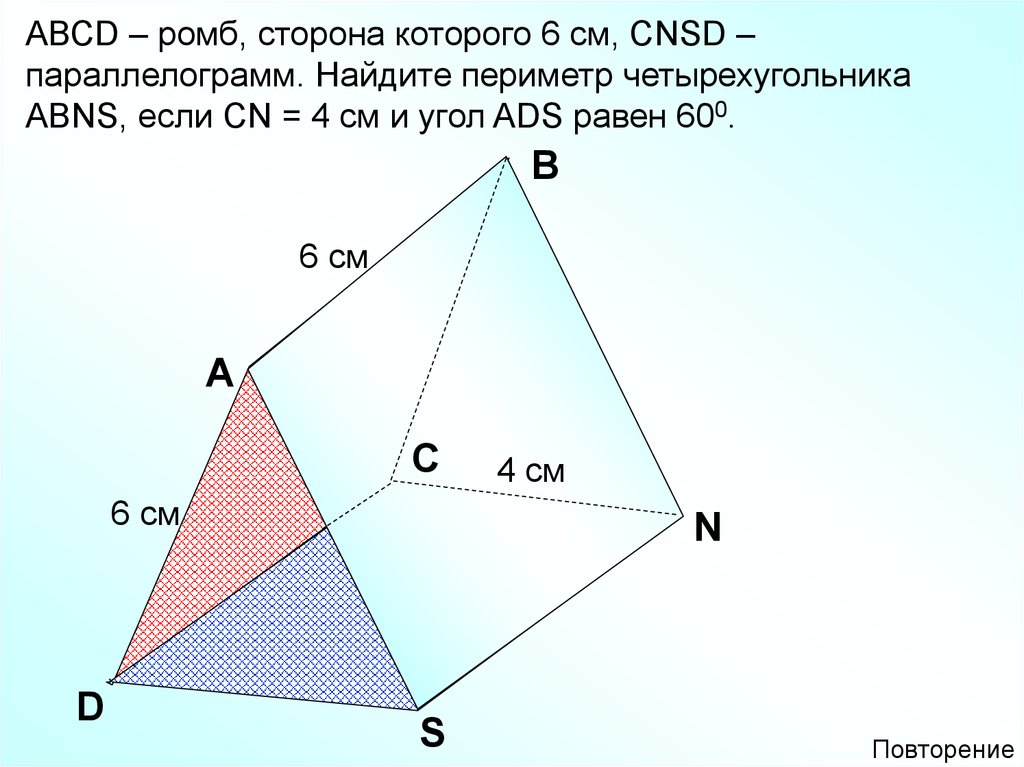
АВСD – ромб, сторона которого 6 см, СNSD –
параллелограмм. Найдите периметр четырехугольника
АВNS, если СN = 4 см и угол ADS равен 600.
В
6 см
A
C
6 см
D
4 см
N
S
Повторение

3.

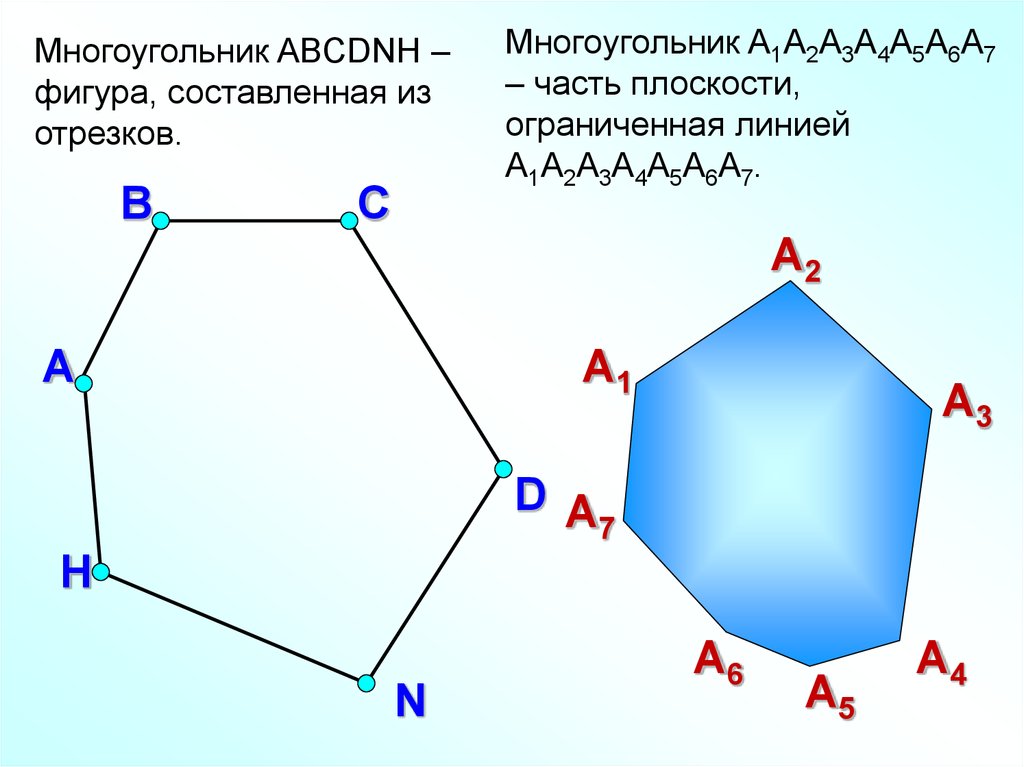
Многоугольник ABCDNH –
фигура, составленная из
отрезков.
В
С
Многоугольник A1А2А3А4А5А6А7
– часть плоскости,
ограниченная линией
A1А2А3А4А5А6А7.
А2
А
А1
А3
D А
7
H
N
А6
А5
А4

4.

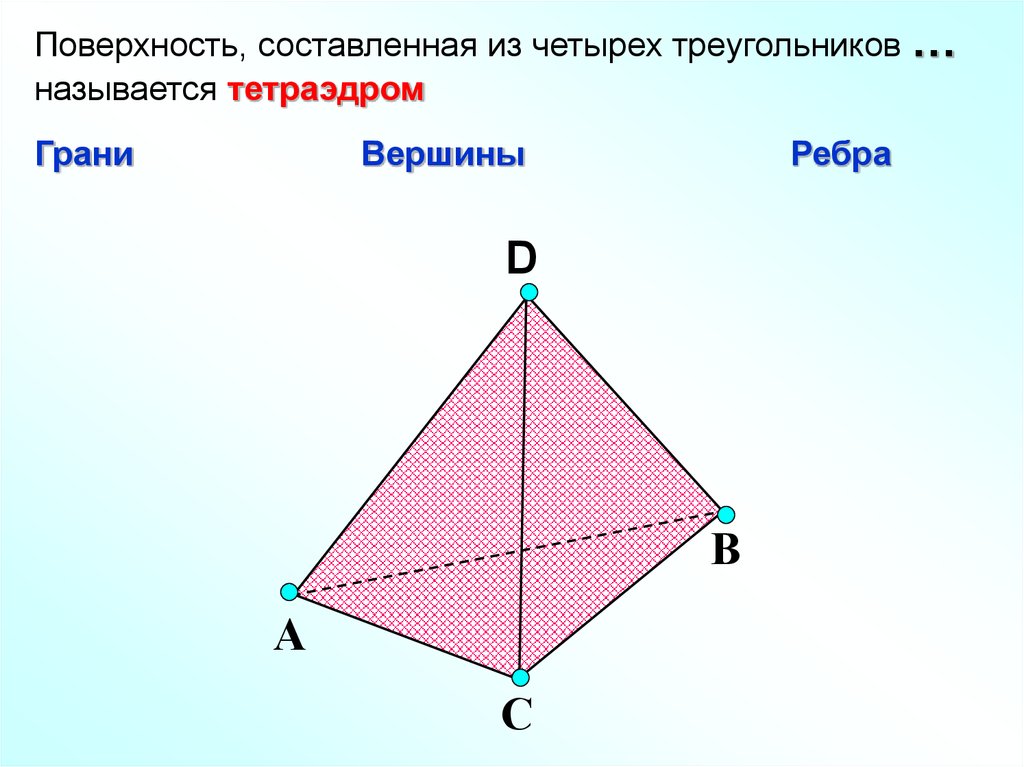
Поверхность, составленная из четырех треугольников …
называется тетраэдром
Грани
Вершины
Ребра
D
В
А
С

5.

Тетраэдр.
Слово составлено из греческих
«четыре»
и
- «основание».
,/
Буквальное значение – «четырехгранник».
По-видимому, термин впервые
S
S
употреблен Евклидом.
После Платона чаще
встречается «пирамида»
В
А
С

6.

Противоположные ребра
D
D
В
В
А
А
С
основание
С

7.

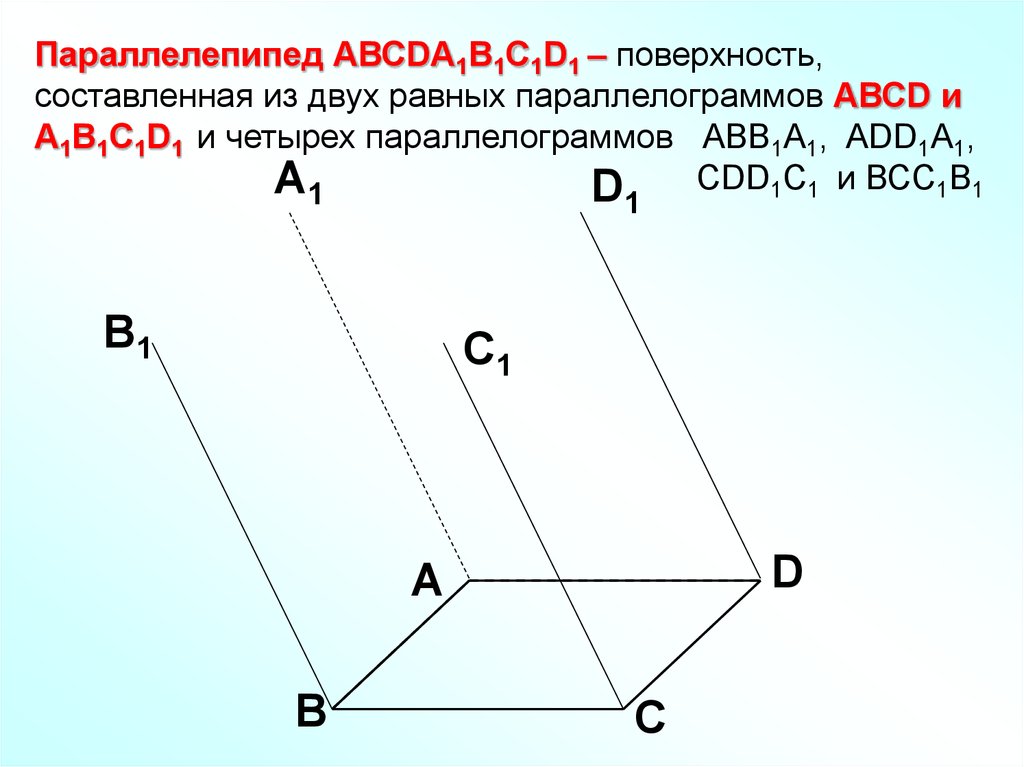
Параллелепипед АВСDA1B1C1D1 – поверхность,
составленная из двух равных параллелограммов АВСD и
A1B1C1D1 и четырех параллелограммов АВВ1А1, ADD1A1,
CDD1C1 и ВСС1В1
A1
D
1
B1
С1
D
А
В
С

8.

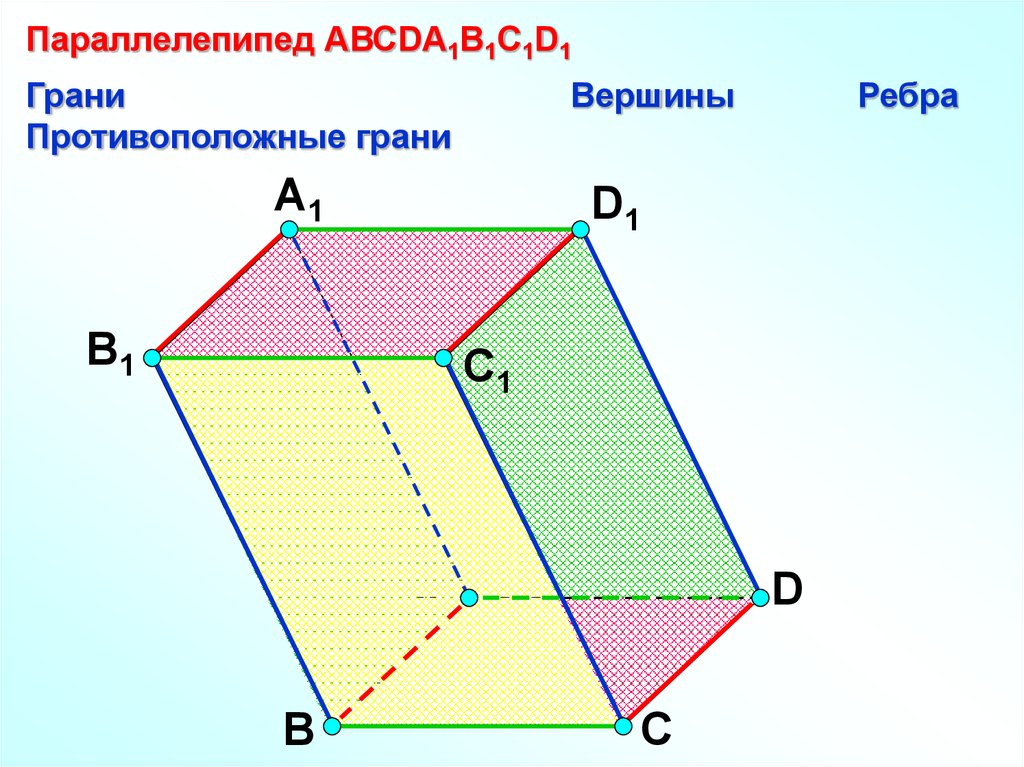
Параллелепипед АВСDA1B1C1D1
Грани
Противоположные грани
Вершины
A1
Ребра
D1
B1
С1
D
А
В
С

9.

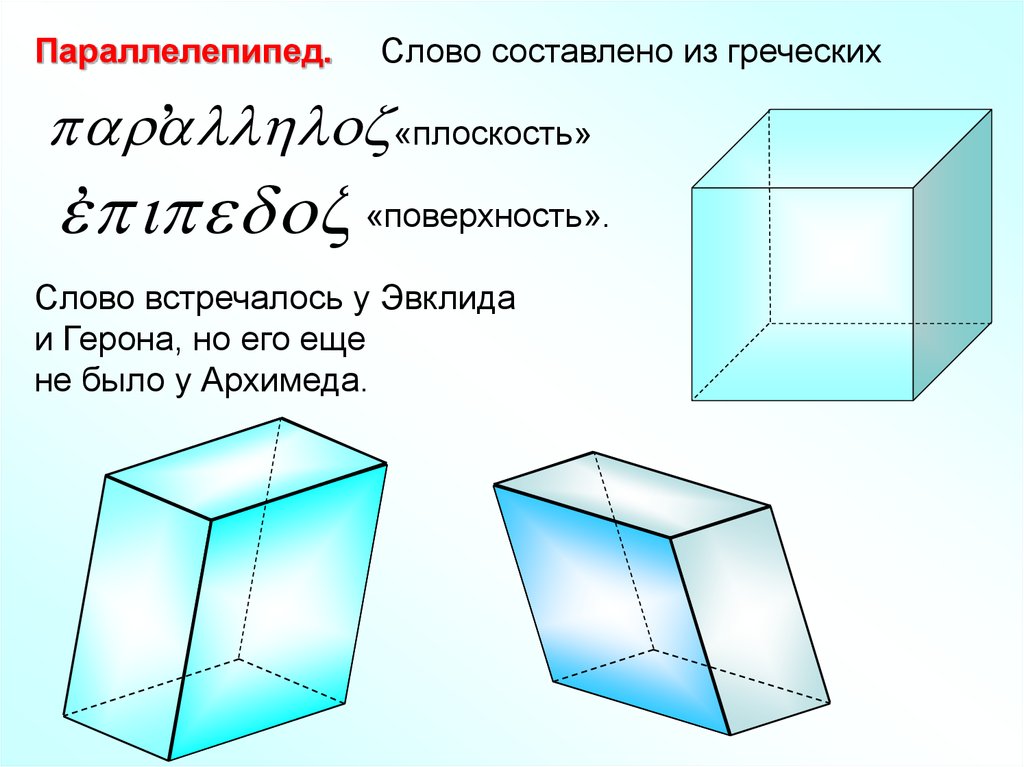
Параллелепипед.
Слово составлено из греческих
,
«плоскость»
«поверхность».
,
Слово встречалось у Эвклида
и Герона, но его еще
не было у Архимеда.

10.

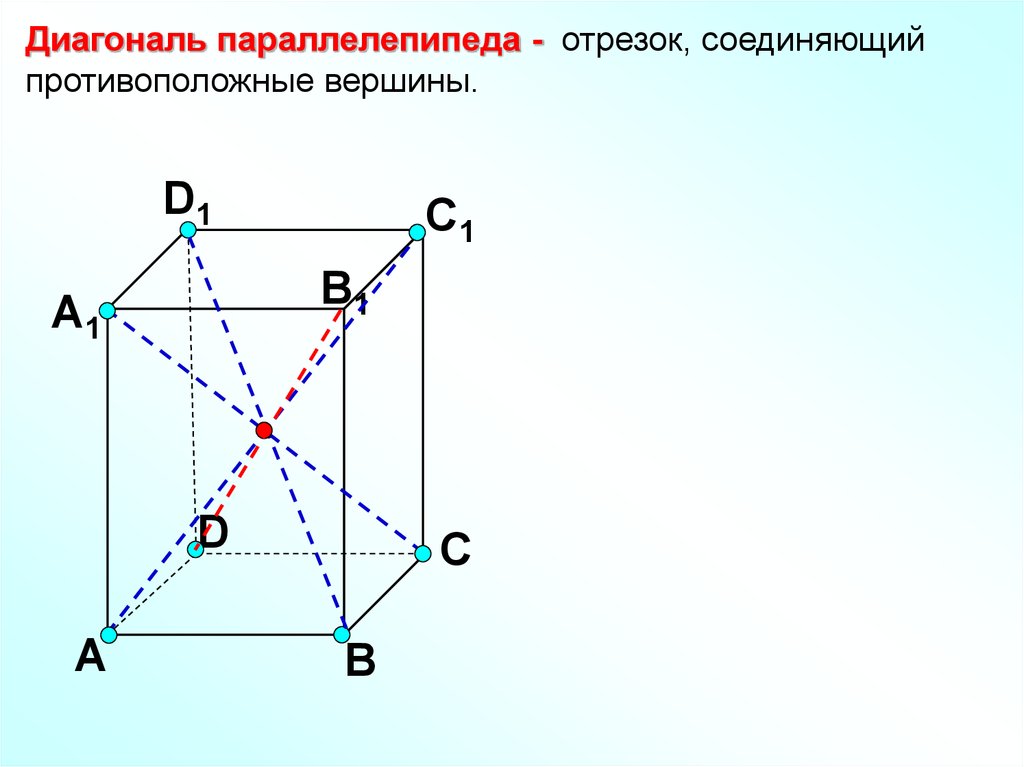
Диагональ параллелепипеда - отрезок, соединяющий
противоположные вершины.
D1
С1
B1
А1
D
А
С
В

11.

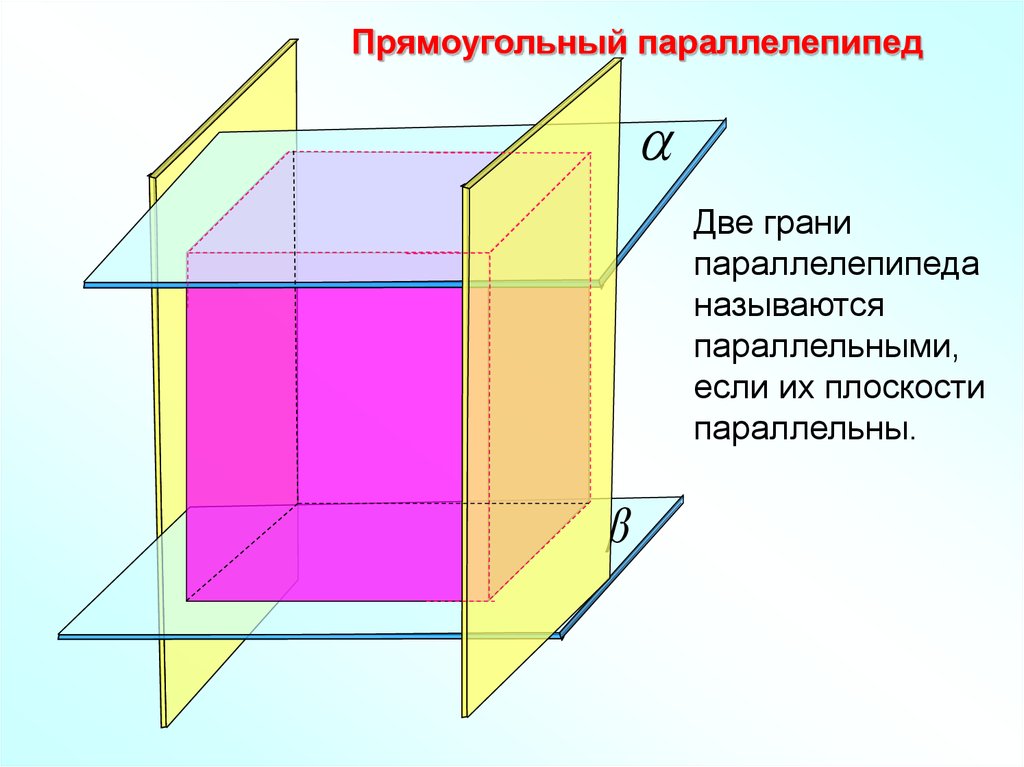
Прямоугольный параллелепипед
Две грани
параллелепипеда
называются
параллельными,
если их плоскости
параллельны.

12.

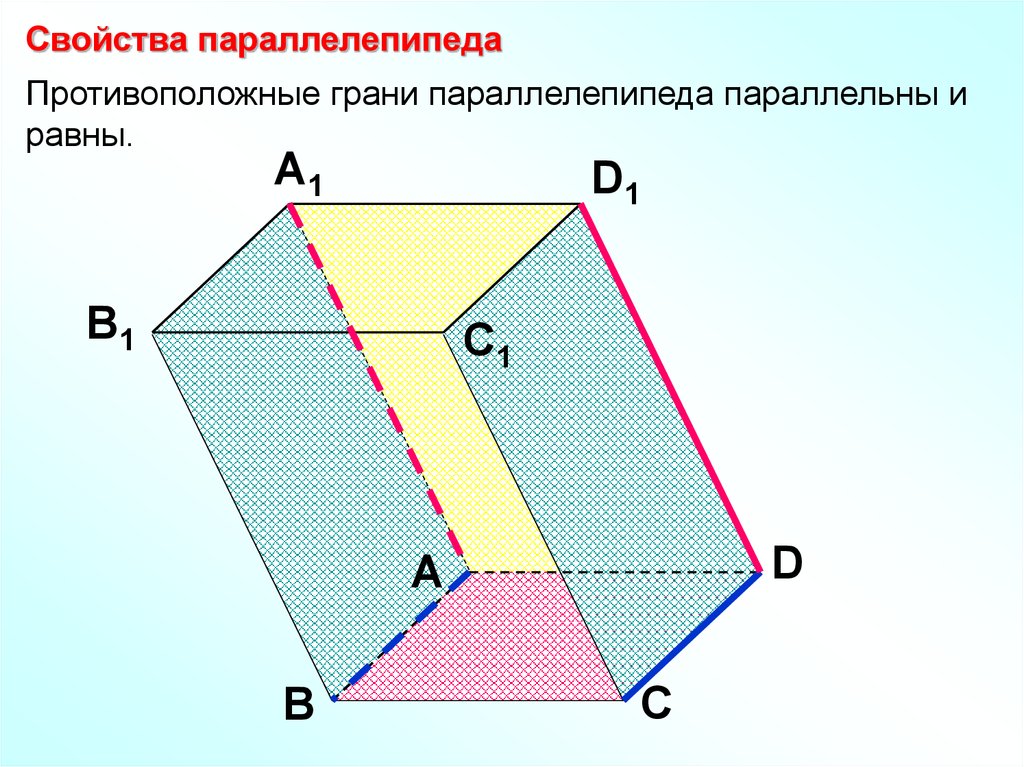
Свойства параллелепипеда
Противоположные грани параллелепипеда параллельны и
равны.
A1
D1
B1
С1
D
А
В
С

13.

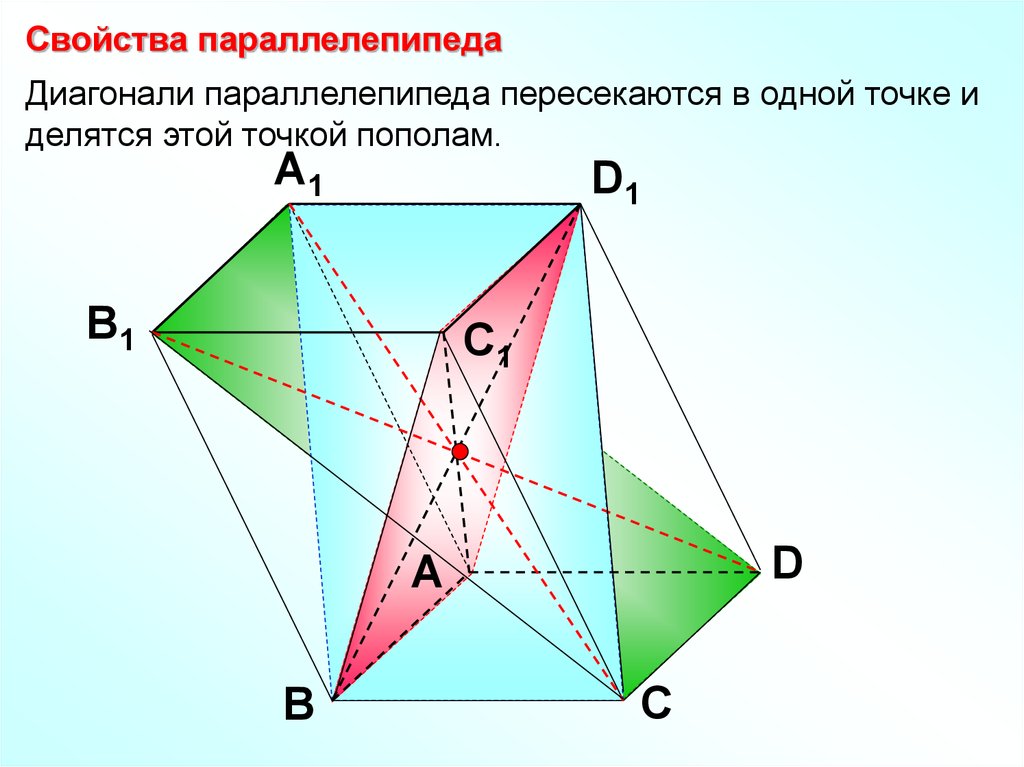
Свойства параллелепипеда
Диагонали параллелепипеда пересекаются в одной точке и
делятся этой точкой пополам.
A1
D1
B1
С1
D
А
В
С

14.

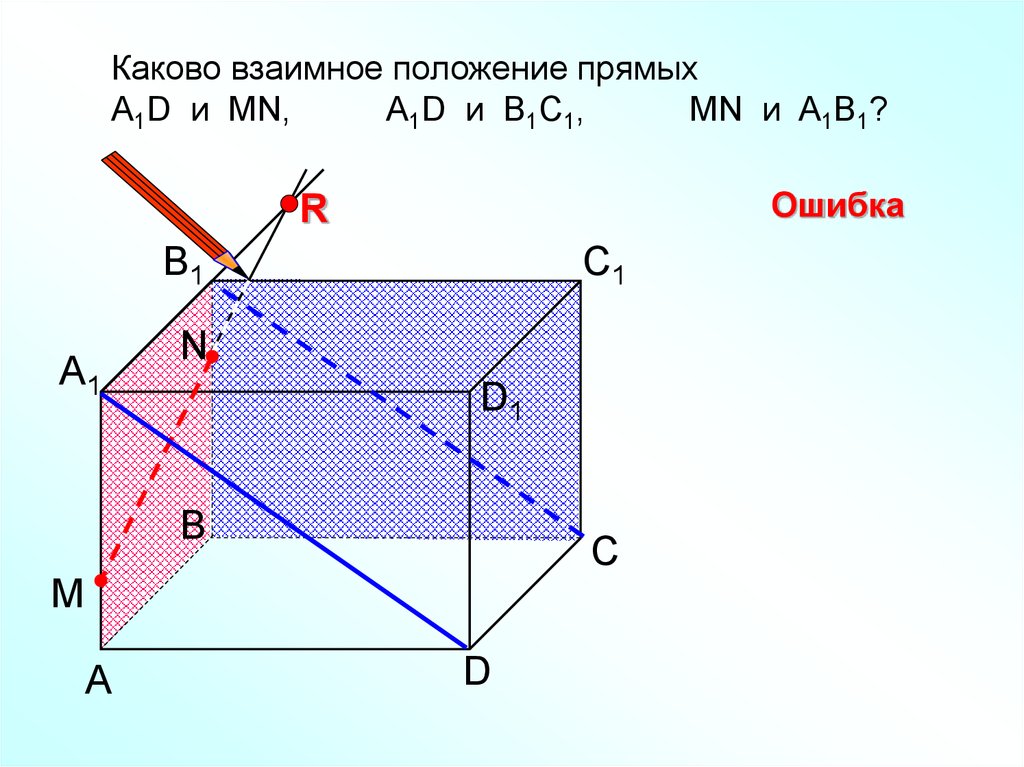
Каково взаимное положение прямых
А1D и MN,
А1D и В1С1,
МN и A1B1?
Ошибка
R
С1
B1
А1
N
D1
В
С
M
А
D

15.

F и E - средины ребер куба. Определите взаимное
расположение прямых и угол между прямыми EF и AC.
B1
F
С1
E
А1
D1
В
А
С
D

16.

B1
С1
А1
D1
В
А
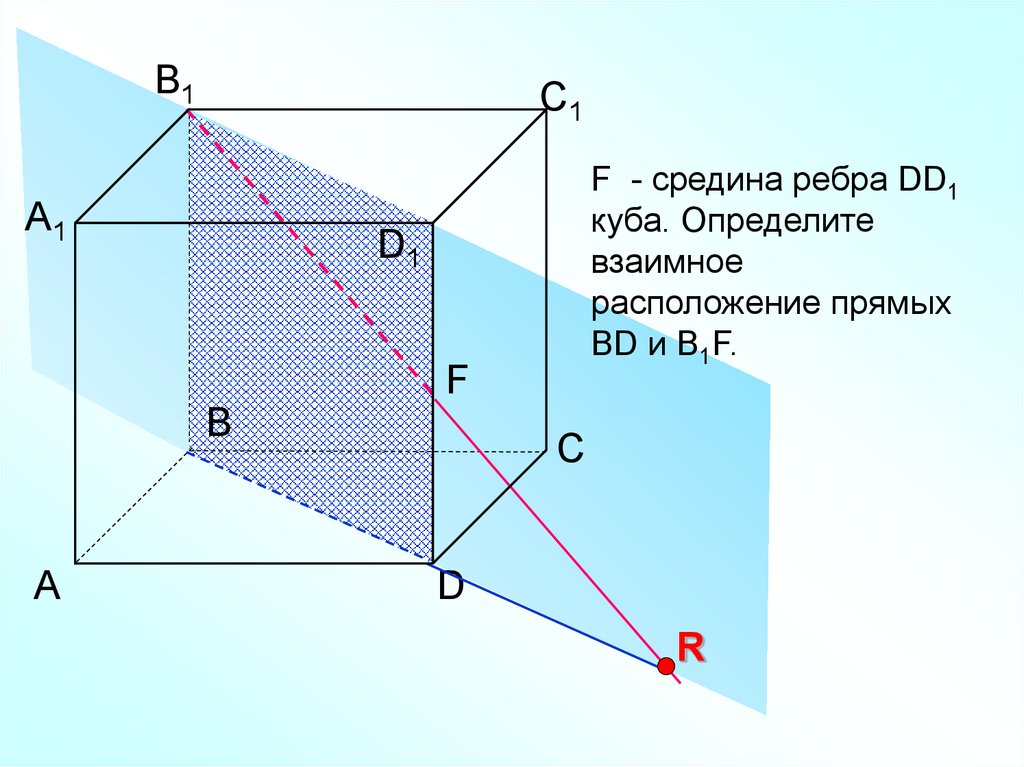
F - средина ребра DD1
куба. Определите
взаимное
расположение прямых
BD и B1F.
F
С
D
R

17.

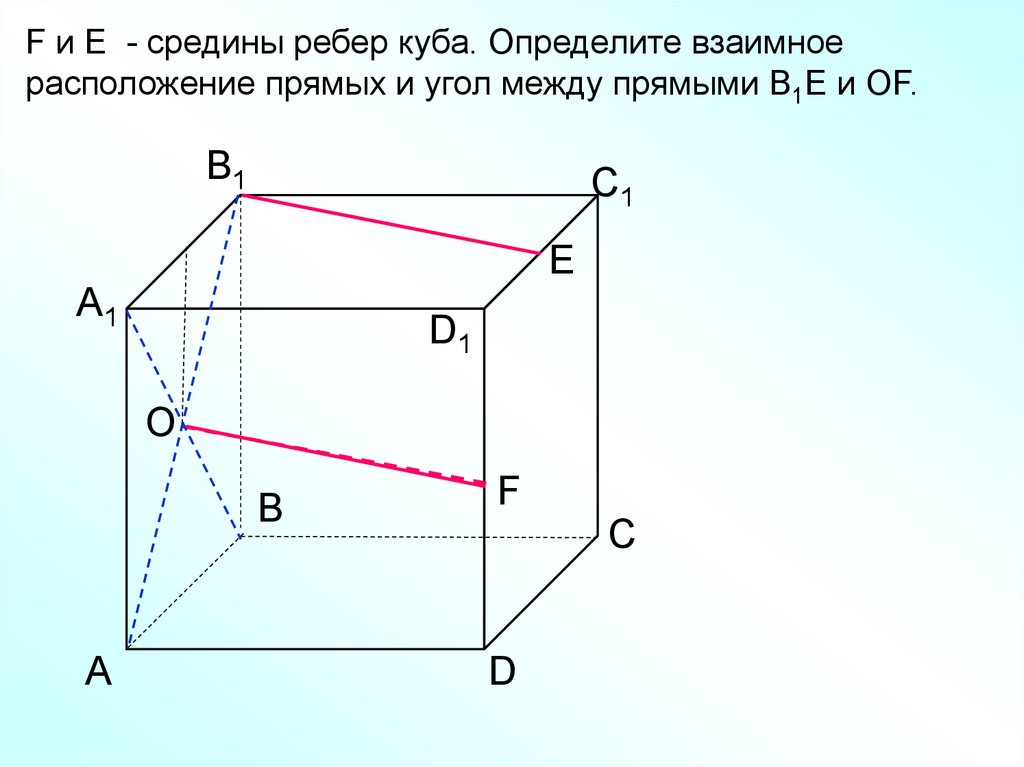
F и E - средины ребер куба. Определите взаимное
расположение прямых и угол между прямыми В1Е и ОF.
B1
С1
E
А1
D1
О
В
А
F
D
С

18.

B1
С1
Е
А1
D1
В
А
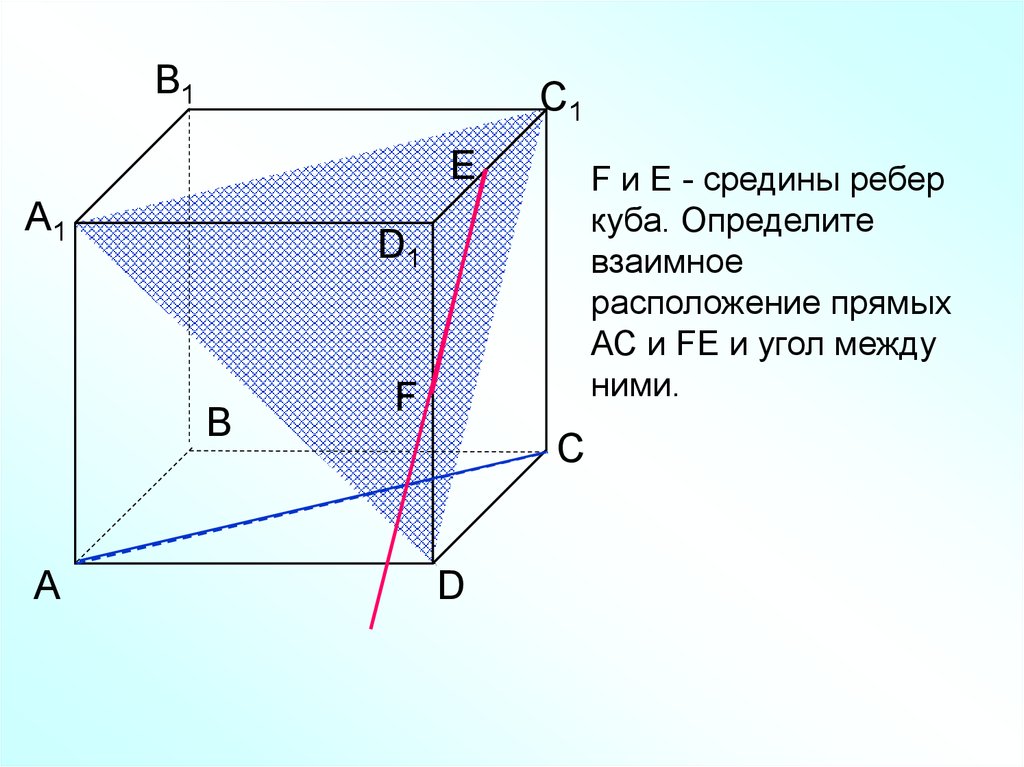
F и Е - средины ребер
куба. Определите
взаимное
расположение прямых
АС и FЕ и угол между
ними.
F
С
D

19.

B1
С1
F и Е - средины ребер
куба. Определите
взаимное
расположение прямых
ОЕ и FВ1.
Е
А1
D1
О
В
А
F
D
С

20.

F, Е, N, M - средины
ребер тетраэдра.
Определите взаимное
расположение прямых
NM и FЕ и угол между
ними.
D
N
E
А
С
M
F
В

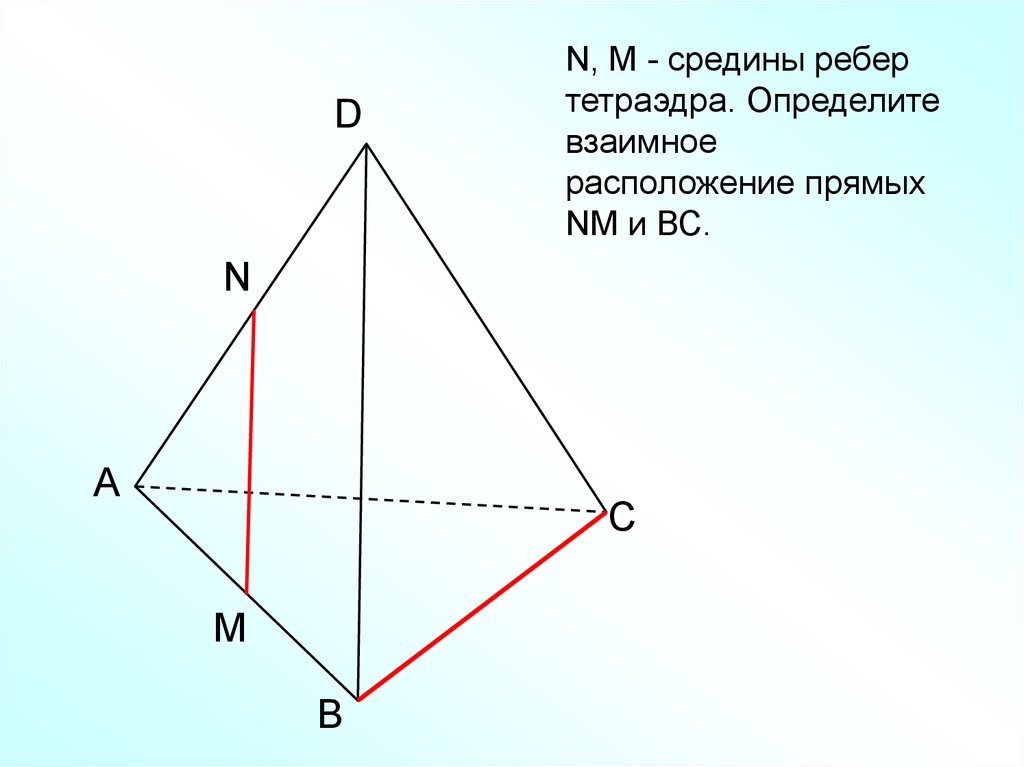
21.

D
N, M - средины ребер
тетраэдра. Определите
взаимное
расположение прямых
NM и ВС.
N
А
С
M
В

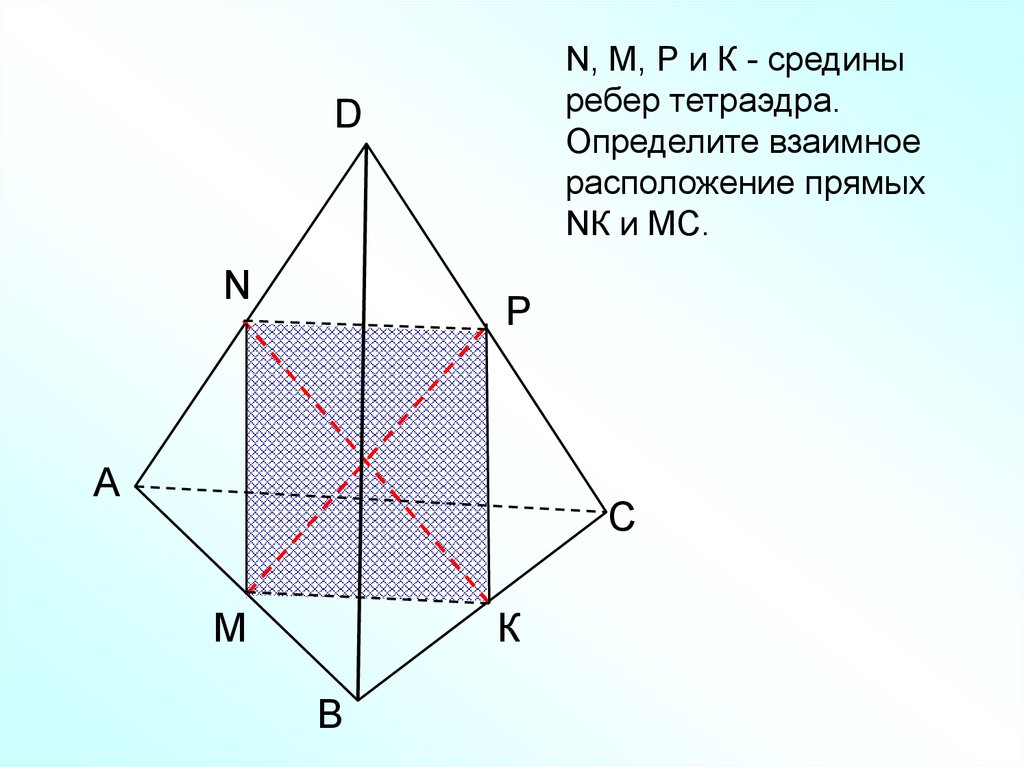
22.

N, M, Р и К - средины
ребер тетраэдра.
Определите взаимное
расположение прямых
NК и МС.
D
N
Р
А
С
К
M
В

23.

N, Р и К - средины
ребер тетраэдра.
Определите взаимное
расположение прямых
NВ и РК.
D
N
Р
А
С
К
В

24.

N и Р - средины ребер
тетраэдра. Определите
взаимное
расположение прямой
NР и плоскости АСD
D
Р
А
N
В
С

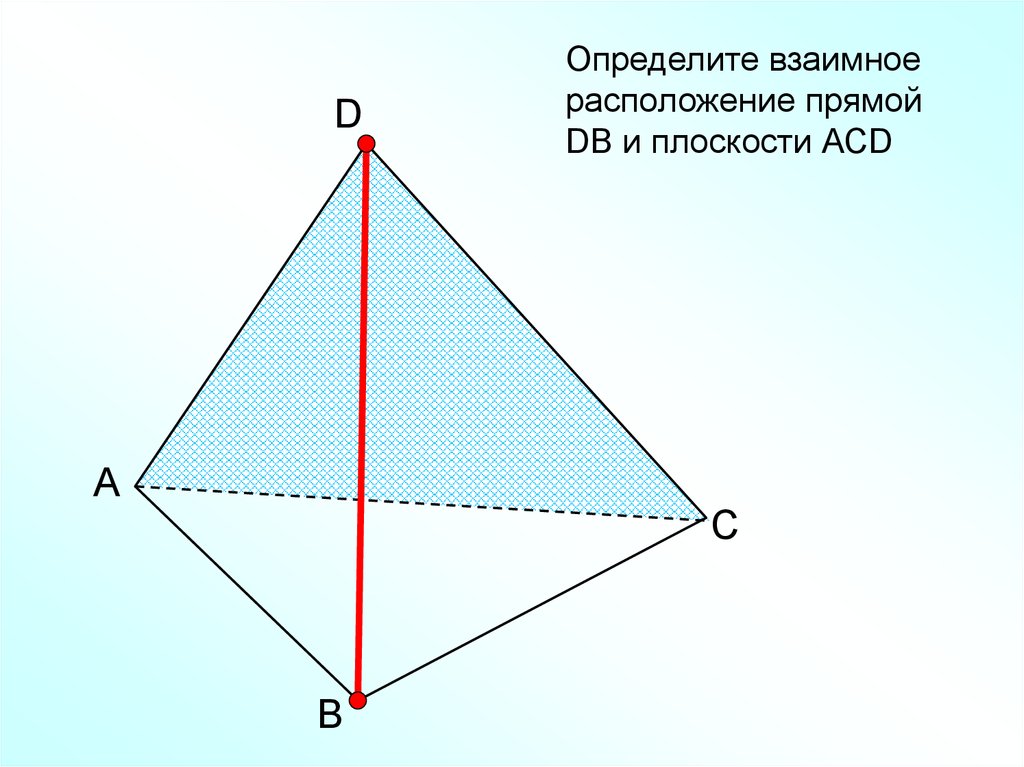
25.

D
А
Определите взаимное
расположение прямой
DВ и плоскости АСD
С
В

26.

F, S, N и Р - средины
ребер тетраэдра.
Определите взаимное
расположение прямой
CF и плоскости NPS
D
Р
А
N
С
F
S
В

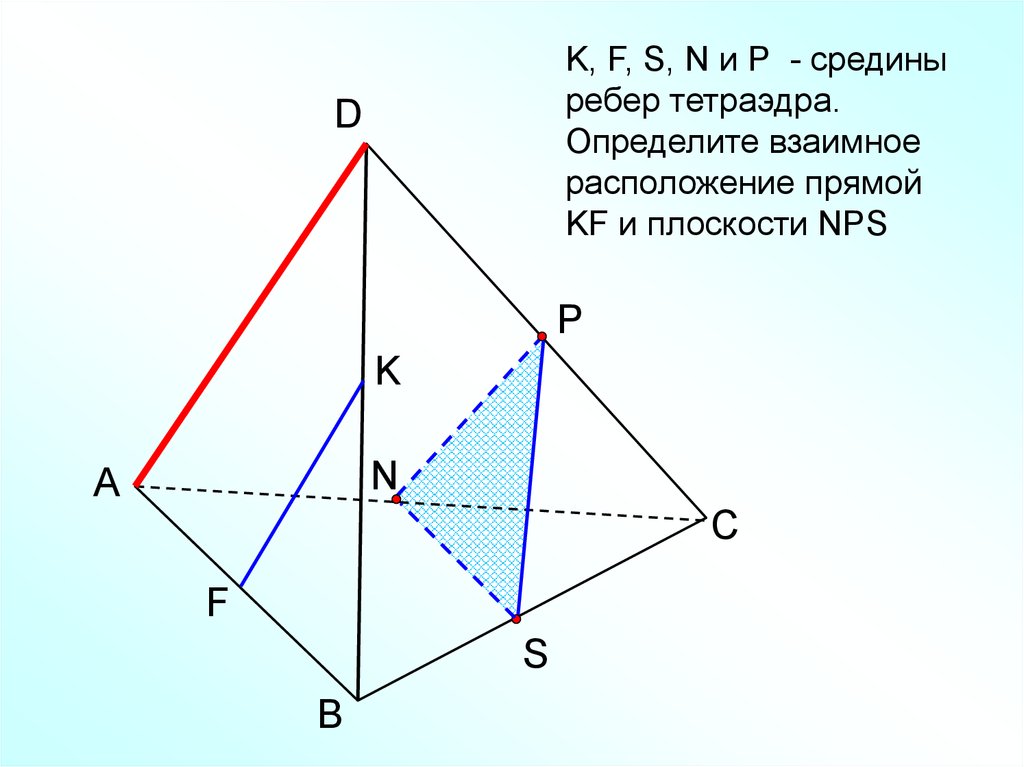
27.

K, F, S, N и Р - средины
ребер тетраэдра.
Определите взаимное
расположение прямой
KF и плоскости NPS
D
Р
K
А
N
С
F
S
В