Похожие презентации:
Положение прямой относительно плоскостей проекций
1.
Положение прямойотносительно
плоскостей проекций
2.
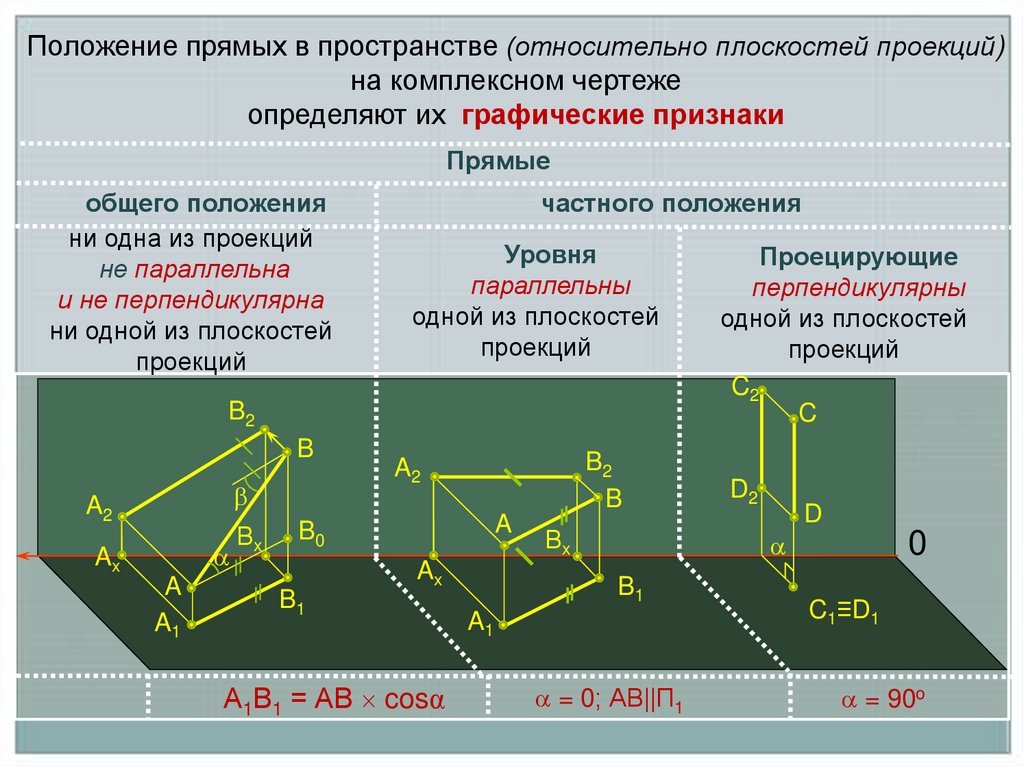
Положение прямых в пространстве (относительно плоскостей проекций)на комплексном чертеже
определяют их графические признаки
Прямые
общего положения
ни одна из проекций
не параллельна
и не перпендикулярна
ни одной из плоскостей
проекций
частного положения
Уровня
параллельны
одной из плоскостей
проекций
B2
B
A2
Ax
A
A1
Вx
B2
B
A2
A
B0
Ax
B1
А1В1 = АВ cosα
Вx
Проецирующие
перпендикулярны
одной из плоскостей
проекций
C2
C
D2
D
B1
A1
= 0; АВ||П1
0
C1≡D1
= 90o
3.
Линии уровня4.
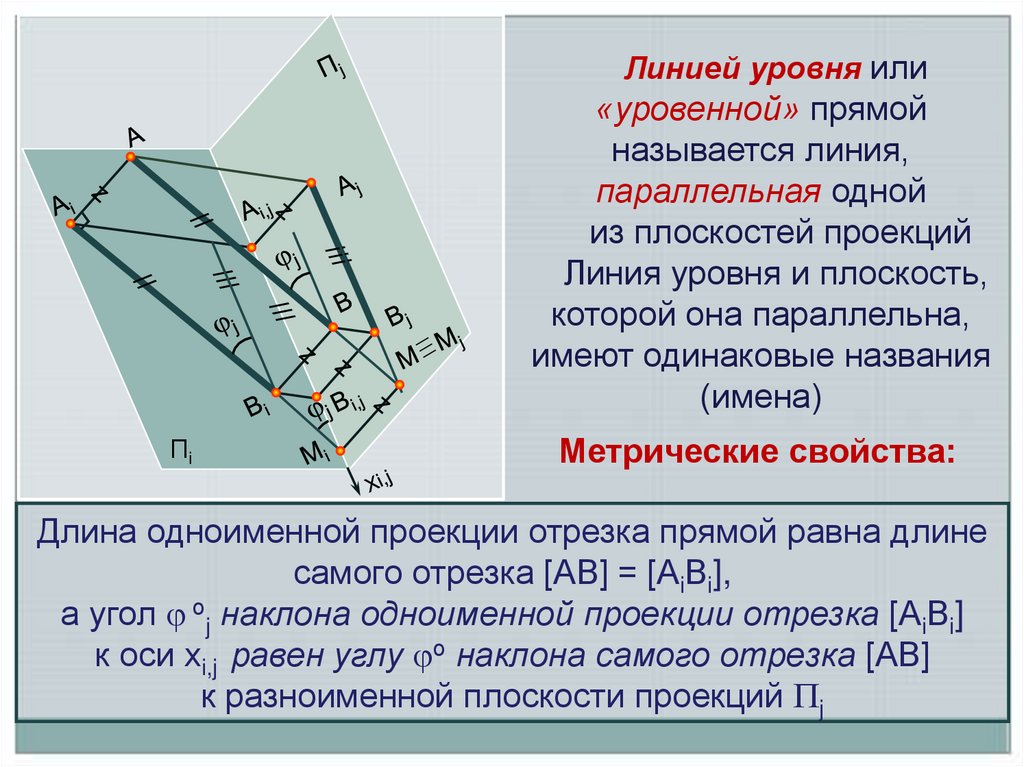
Линией уровня или«уровенной» прямой
называется линия,
параллельная одной
из плоскостей проекций
Линия уровня и плоскость,
которой она параллельна,
имеют одинаковые названия
(имена)
Пi
Метрические свойства:
Длина одноименной проекции отрезка прямой равна длине
самого отрезка [АВ] = [АiВi],
а угол оj наклона одноименной проекции отрезка [АiВi]
к оси хi,j равен углу о наклона самого отрезка [АВ]
к разноименной плоскости проекций j
5.
h – горизонтальz(х2,3)
Z(х2,3)
h3
h2
h3
h2
h
h1
П2
Zh
П3
П1
Y(х1,3)
Zh
Х1,2
Zh
Zh
2 3
Y(х1,3)
6.
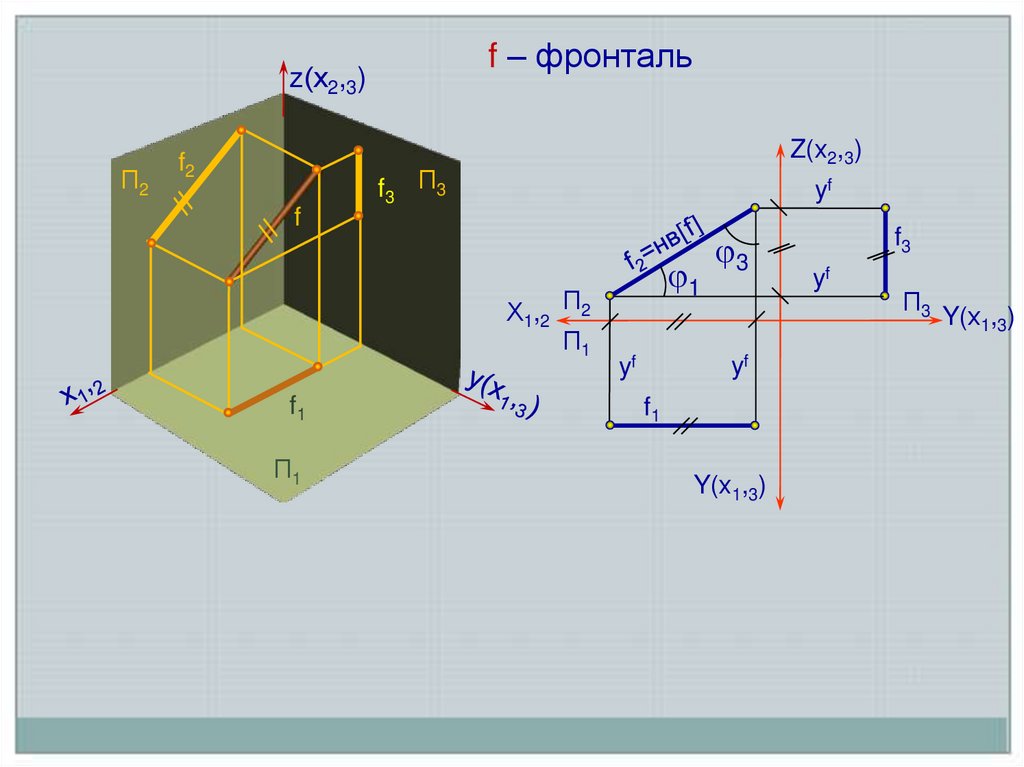
f – фронтальz(х2,3)
П2
f2
Z(х2,3)
f 3 П3
yf
f
Х1,2 П2
П1
f1
П1
1
3
yf
yf
f1
Y(х1,3)
f3
yf
П3
Y(х1,3)
7.
р – профильная прямаяZ(Х2,3)
z(х2,3)
хр
р3
р
Х1,2
р1
3
р2
р3
р2
yр
хр
П2
П1
yр
р1
yf
1
П3
Y(Х1,3)
хр
хр
Y(Х1,3)
8.
z(х2,3)nj
ni
n
nq
Проецирующей
называется прямая,
перпендикулярная какойлибо плоскости проекций:
n Пi в пространстве
одноименная проекция
проецирующей прямой
вырождается в точку,
а разноименная –
перпендикулярна оси,
разделяющей ее
с одноименной проекцией
9.
Z(Х2,3)а2
а3
c2
Х1,2
П1
b3
П3
Y(Х1,3)
c1
а1
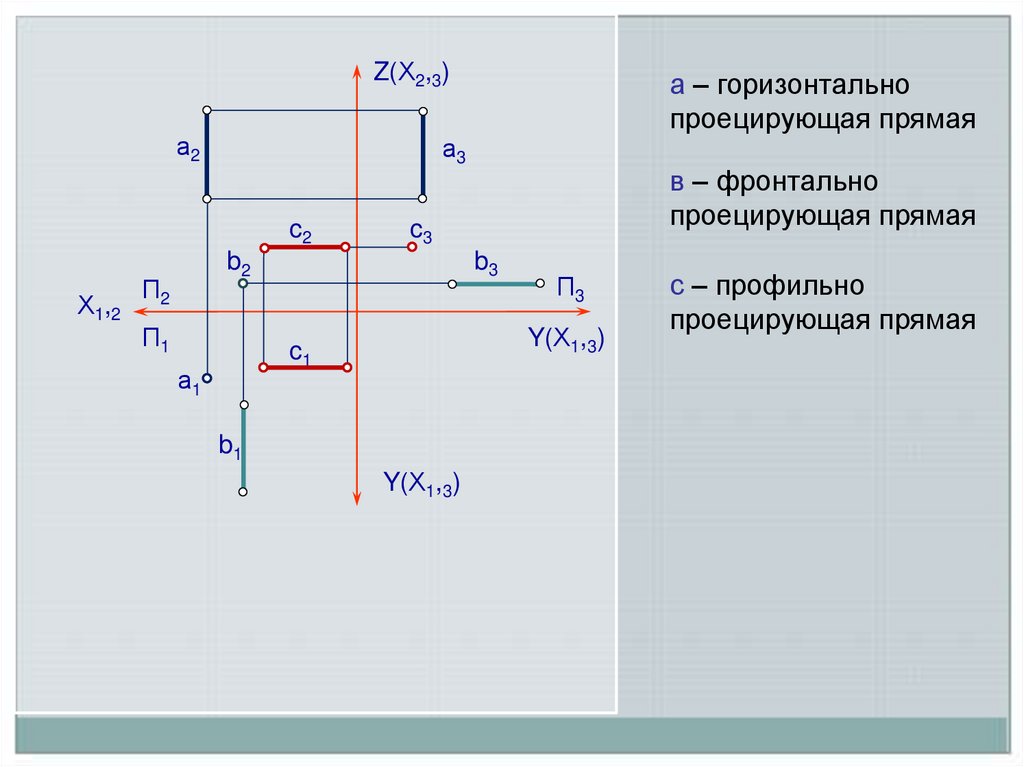
в – фронтально
проецирующая прямая
c3
b2
П2
а – горизонтально
проецирующая прямая
b1
Y(Х1,3)
с – профильно
проецирующая прямая





 Математика
Математика Инженерная графика
Инженерная графика








