Начертательная геометрия. Положение прямой относительно плоскости проекций. (Лекция 2)

1. Начертательная геометрия

2.

ЛЕКЦИЯ №2

3.

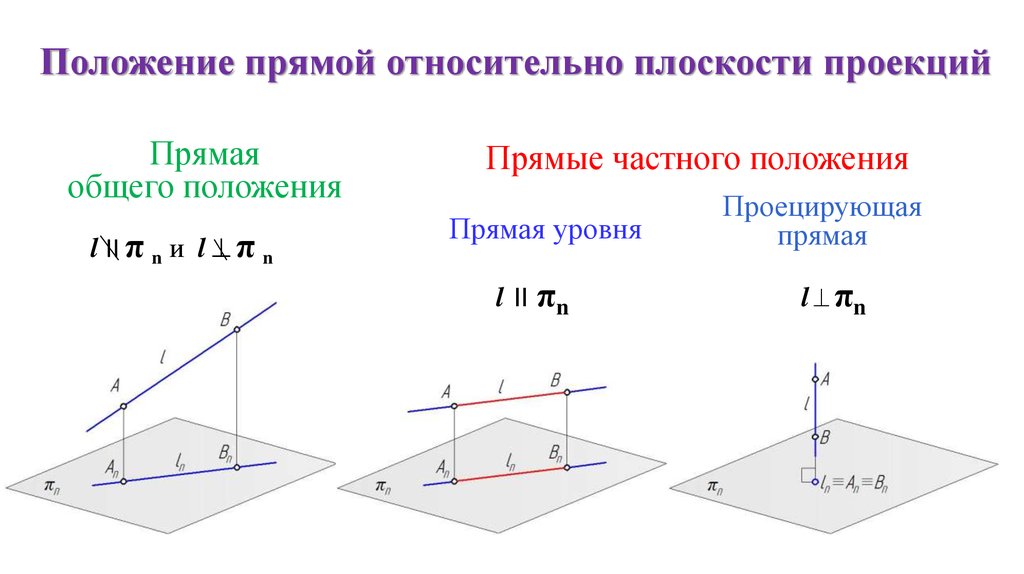
Положение прямой относительно плоскости проекций
Прямая
общего положения
l II π n и l π n
Прямые частного положения
Прямая уровня
l II
πn
Проецирующая
прямая
l πn

4.

ПРЯМЫЕ
ОБЩЕГО
ПОЛОЖЕНИЯ
ЧАСТНОГО
ПОЛОЖЕНИЯ
УРОВНЯ
ПРОЕЦИРУЮЩИЕ

5.

Прямая общего положения
l1 II π 1 и l1 π 1
l2 II π 2 и l2 π 2
l1 II x12 и l2 II x12
l1 x12
и l2 x12

6.

Прямые частного положения
Это прямые параллельные или перпендикулярные
одной из плоскостей проекций
l II πn или l πn

7.

Прямая уровня
Это прямая параллельная одной из плоскостей
проекций
l II πn

8.

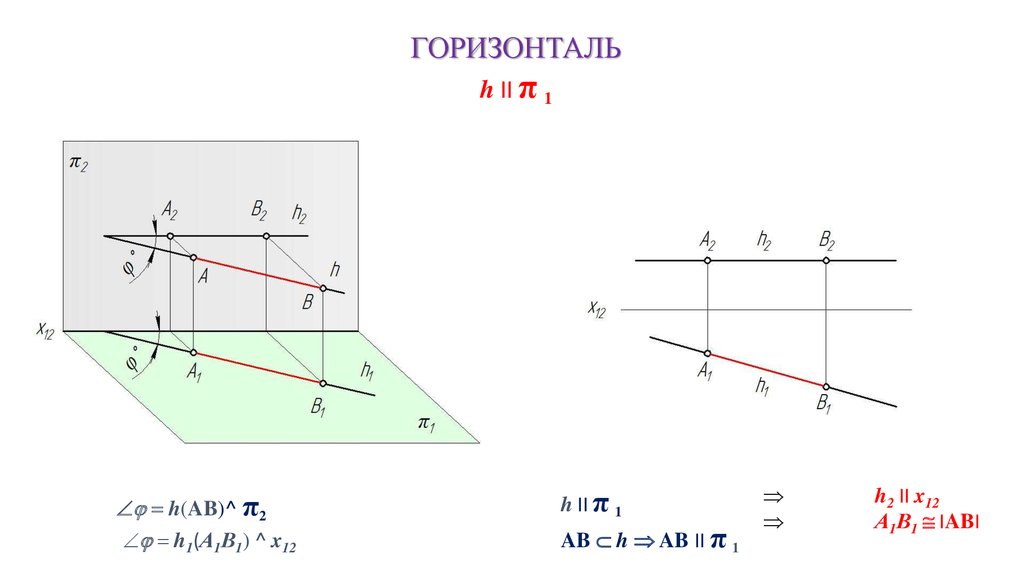
ГОРИЗОНТАЛЬ
h II π 1
h(AB)^ π2
h1(А1В1) ^ x12
h II π 1
AB h AB II π 1
h2 II x12
А1В1 IABI

9.

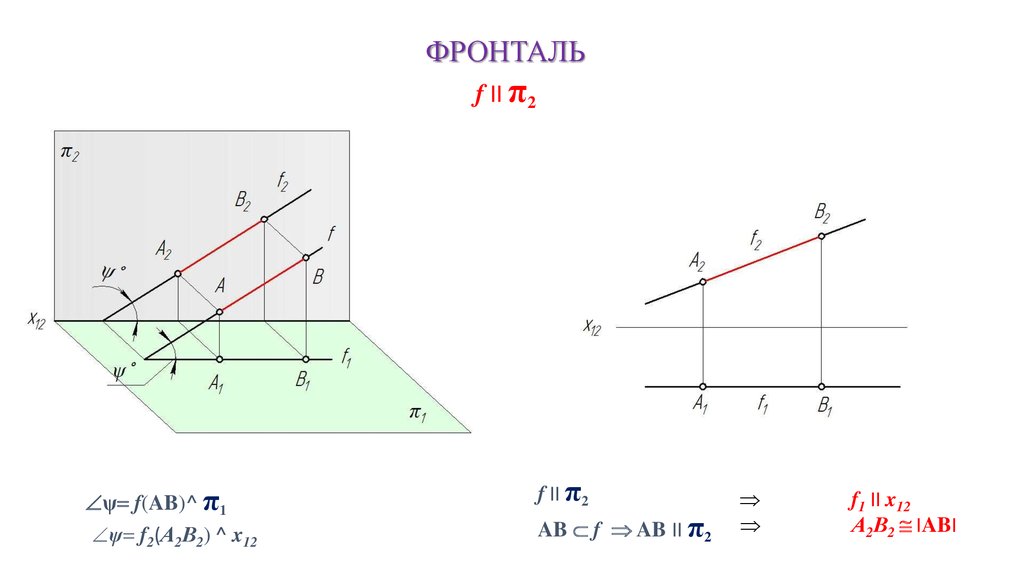
ФРОНТАЛЬ
f II π2
ψ f(AB)^ π1
ψ f2(А2В2) ^ x12
f II π2
AB f AB II π2
f1 II x12
А2В2 IABI

10.

ПРОФИЛЬНАЯ ПРЯМАЯ
p II π3
р II π3
AB р AB II π3
р1 II y , р2 II z
А3В3 IABI

11.

Проецирующая прямая
Это прямая перпендикулярная одной из
плоскостей проекций
l πn

12.

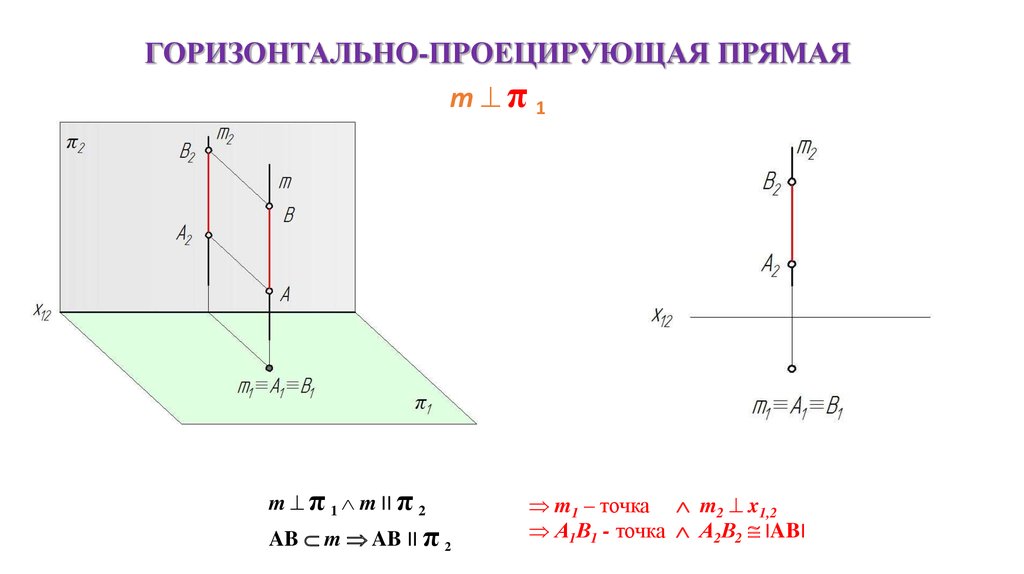
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
m π1
m π 1 m II π 2
AB m AB II π 2
m1 – точка m2 x1,2
А1В1 - точка А2В2 IABI

13.

ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
n π2
n π 2 n II π 1
AB n AB II π 1
n2 – точка n1 x1,2
А2В2 - точка А1В1 IABI

14.

Характерная особенность эпюра
проецирующей прямой –
одна из проекций прямой точка

15.

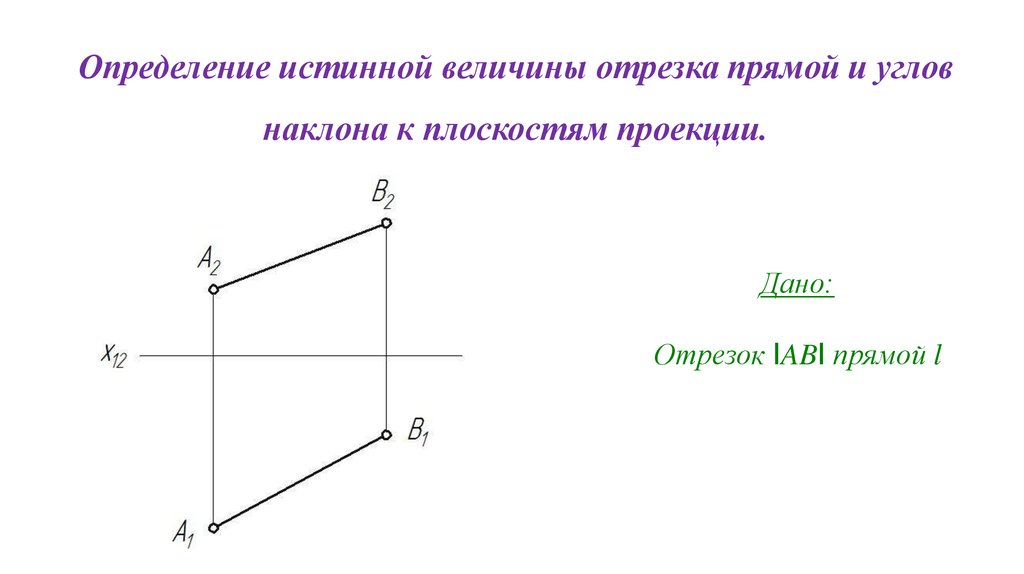
Определение истинной величины отрезка прямой и углов
наклона к плоскостям проекции.
Дано:
Отрезок IABI прямой l

16.

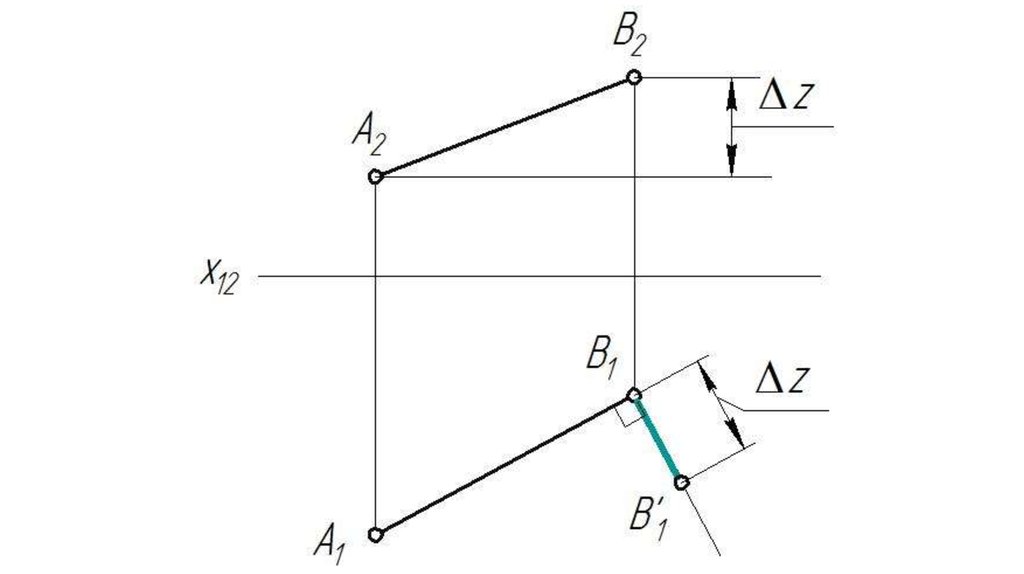
17.

18.

IABI^ π1

19.

20.

ψ IABI ^ π2

21.

Взаимное положение двух
прямых

22.

Пересекающиеся прямые
m∩n=K
m1 ∩ n1 = K1
m2 ∩ n2 = K2
K1K2 x1,2

23.

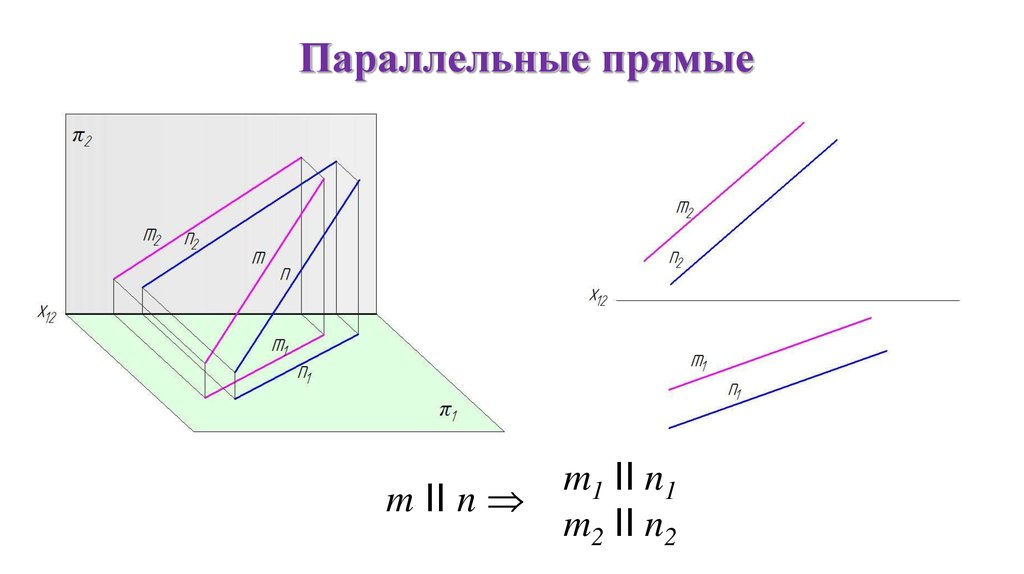
Параллельные прямые
m II n
m1 II n1
m2 II n2

24.

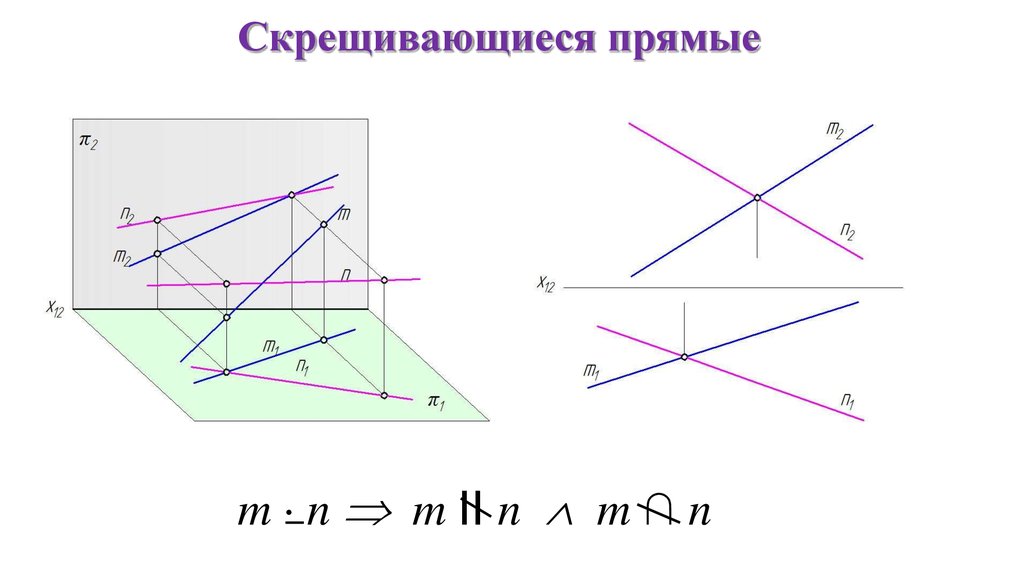
Скрещивающиеся прямые
m n m II n m ∩ n

25.

Взаимно перпендикулярные
прямые
Если
m l,
m l m n,
m II πn ,
l πn ,
то
mn ln

26.

Теорема о проецировании прямого угла.
Если хотя бы одна сторона прямого
угла параллельна плоскости проекций,
а вторая ей не перпендикулярна, то
угол на эту плоскость проецируется в
натуральную величину.

27.

Поверхности

28.

Плоскость
Плоскость - это один из видов поверхности (плоская
поверхность).
Положение 8.
Плоскости бесконечны и не прозрачны.

29.

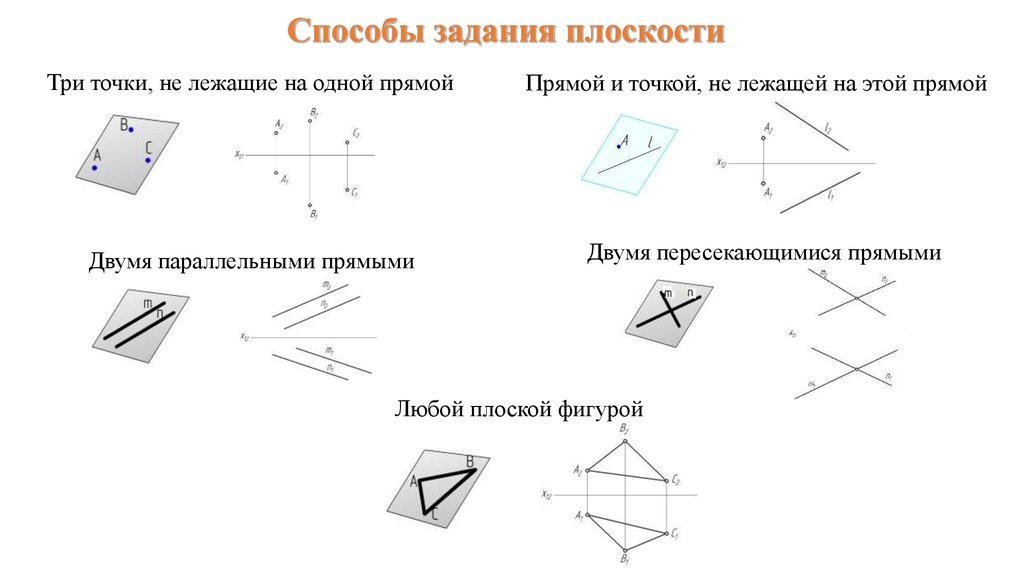
Способы задания плоскости
Три точки, не лежащие на одной прямой
Двумя параллельными прямыми
Прямой и точкой, не лежащей на этой прямой
Двумя пересекающимися прямыми
Любой плоской фигурой

30.

Положение плоскости относительно плоскостей
проекций
ПЛОСКОСТИ
ЧАСТНОГО
ПОЛОЖЕНИЯ
ОБЩЕГО
ПОЛОЖЕНИЯ
УРОВНЯ
ПРОЕЦИРУЮЩИЕ

31.

Общее положение
Частное положение
Плоскость уровня
U II Пк U Пк
Г II Пк
Проецирующая плоскость
Т Пк

32.

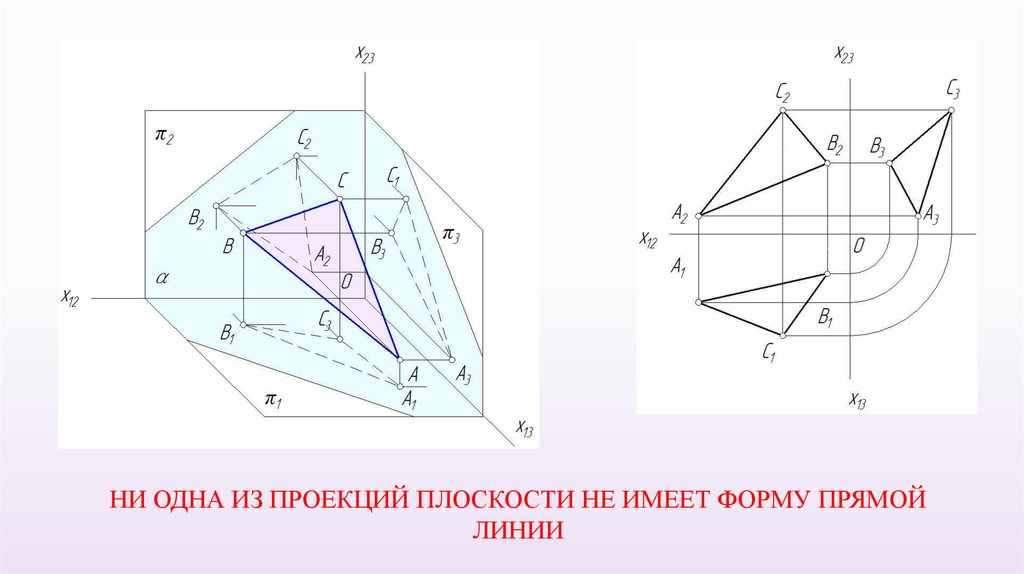
Плоскость общего положения
Плоскость непараллельная и неперпендикулярная плоскостям проекций

33.

НИ ОДНА ИЗ ПРОЕКЦИЙ ПЛОСКОСТИ НЕ ИМЕЕТ ФОРМУ ПРЯМОЙ
ЛИНИИ

34.

Плоскости частного положения
Это плоскости параллельные или перпендикулярные
одной из плоскостей проекций
α II πn или β πn

35.

Проецирующие плоскости
Это плоскости перпендикулярные одной
из плоскостей проекций

36.

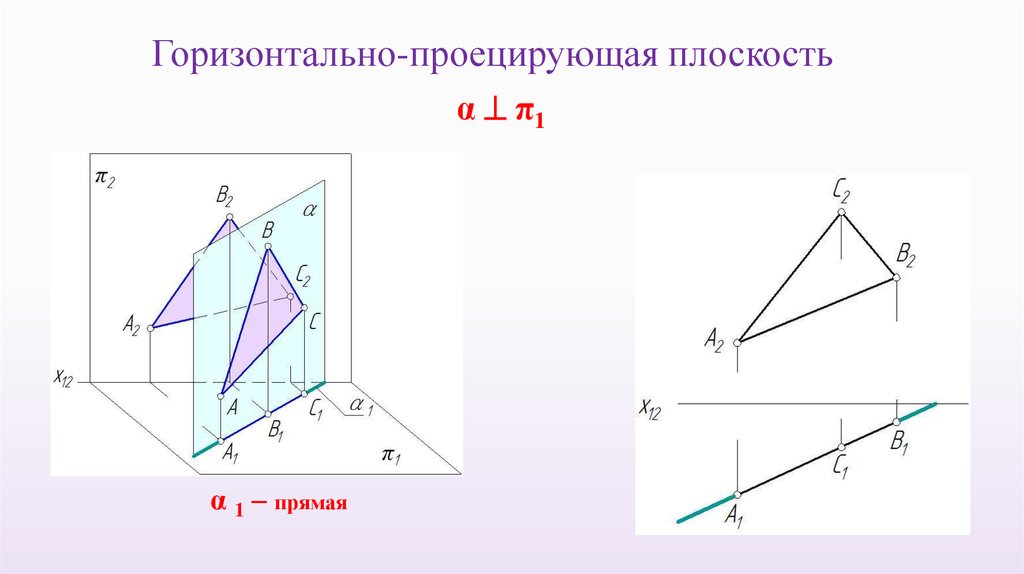
Горизонтально-проецирующая плоскость
α π1
α 1 – прямая

37.

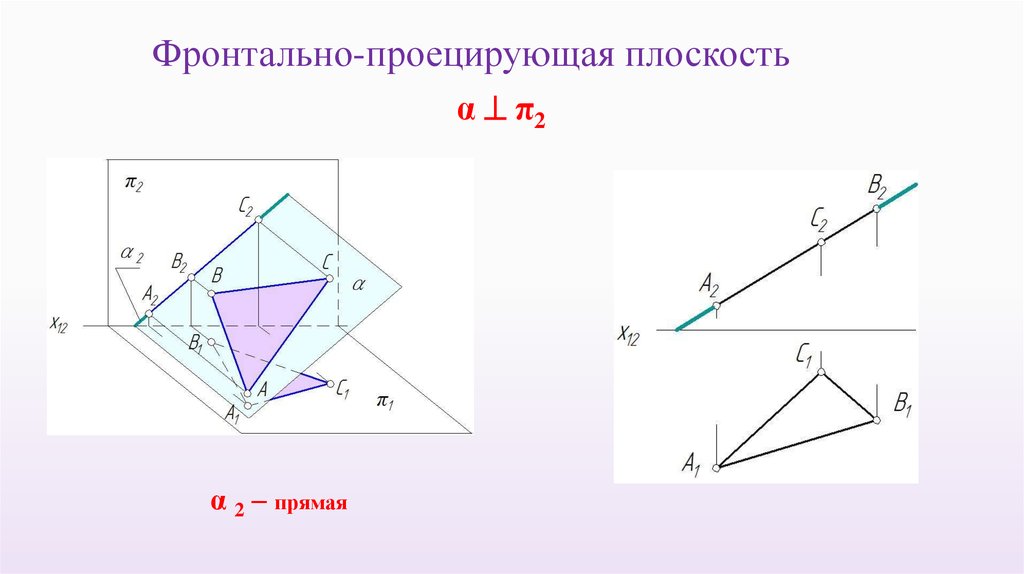
Фронтально-проецирующая плоскость
α π2
α 2 – прямая

38.

Плоскости уровня
Это плоскости параллельные одной из
плоскостей проекций

39.

Горизонтальная плоскость
α 2 – прямая
АВС
α 2II x12
α АВС II π1 А1В1С1 АВС

40.

Фронтальная плоскость
α 1 – прямая
АВС
α 1II x12
α АВС II π2 А2В2С2 АВС

41.

Положение 9
У плоскости частного положения одна из проекций
обязательно имеет форму прямой линии.

42.

Прямая линия
в плоскости

43.

В2
22
12
принадлежит плоскости, если
две точки этой прямой лежат в
Т2
А2
А1
Положение 10. Прямая
l2
плоскости.
11
С2
В1
21
l1
Дано:
Т АВС .
Построить: l Т.
(1 АВ) (2 ВС)
Т1
l (1,2) Т ⇔ (1 Т ) (2 Т)
С1

44.

В2
Положение 11. Прямая принадлежит
Т2
12
плоскости, если имеет с плоскостью одну
l2
А2
общую точку и параллельна какой-либо
прямой расположенной в этой плоскости.
А1
11
В1
С2
Т1
l1
С1
Дано:
Т АВС .
Построить: l Т.
(1 АВ) (2 АС; 2≡2∞) l ||АС
l (1,s) 1 l l ||s
В качестве направления может быть выбрана любая прямая,
принадлежащая плоскости.

45.

Главные линии плоскости
К главным линиям плоскости относятся прямые уровня горизонталь, фронталь и линии наибольшего наклона
плоскости.

46.

Горизонталь плоскости
В2
Т2
А2
12
Это прямая, принадлежащая плоскости,
и параллельная горизонтальной плоскости
h2 проекций
С2
В1
А1
11
h1
Т1
С1
Дано:
Т АВС .
Построить: h Т.
h 1 h2 x12
h (А,1)

47.

Фронталь плоскости
В2
12
Это прямая, принадлежащая плоскости,
и параллельная фронтальной плоскости
проекций
f2
А2
Т2
В1
А1
С2
11
Дано:
Т АВС .
Построить: f Т.
f1
Т1
С1
f 2 f1 x12
f (А,1)

48.

Точка на плоскости
Положение 12. Точка принадлежит плоскости, если она принадлежит
прямой, принадлежащей этой плоскости
А γ А l,l γ

49.

А l ; l (1,s)
(1 n) ; (l || m)
А l ; l (1,2) Т
(1 m ) ; (2 n)
l2
m2
12
A2
m2
Т2
22
n2
l1
11
A1
21
m1
n1
Т1
l2
l1
Т2
A2
12
n2
11
n1
A1
m1
Т1

50.

Взаимное положение двух плоскостей

51.

Параллельные плоскости
Две плоскости параллельны, если две пересекающиеся
прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости.
P2
c2
T2
a2
T2
b2
T1
a1
b1
T1
a2
d2
Т(a∩b);
b2
P(c∩d);
P1
aIIc; bIId;
c1 a1
T II P
d1b1
P2
c2
d2
P1
c1
d1

52.

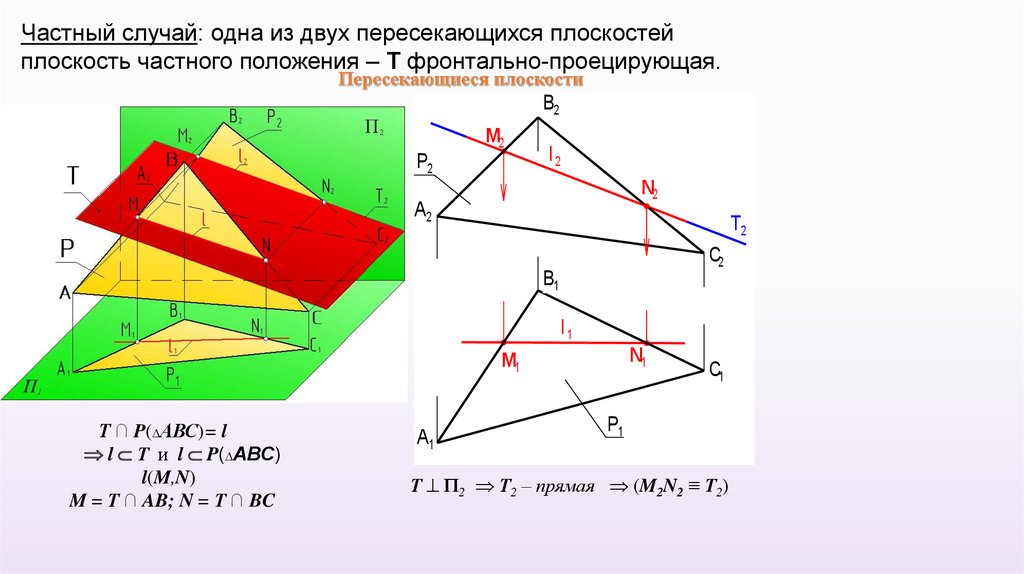
Частный случай: одна из двух пересекающихся плоскостей
плоскость частного положения – Т фронтально-проецирующая.
Пересекающиеся плоскости
B2
M2
P2
l2
N2
A2
T2
C2
B1
l1
N1
M1
Т ∩ P(∆АВС)= l
l Т и l P(∆АВС)
l(M,N)
M = Т ∩ AB; N = Т ∩ BC
A1
C1
P1
Т П2 Т2 – прямая (M2N2 ≡ Т2)

53.

Общий случай: Заданы две плоскости Т и Р общего положения.
Т ∩ P= l(M,N)
Точки M и N могут быть определены как точки пересечения трех плоскостей
М=Т ∩ Р ∩ Δ1; N=Т ∩ Р ∩ Δ2
Δ1 и Δ2 – вспомогательные секущие плоскости - проецирующие.
Δ1 ∩ Т=a1 и Δ1 ∩ Р=b1 a1 ∩ b1=М
Δ2 ∩ Т=a2 и Δ2 ∩ Р=b2 a2 ∩ b2= N
53