Функція та її властивості

1.

ФУНКЦІЯ
ТА ЇЇ
ВЛАСТИВОСТІ

2.

ФУНКЦІЯ – ЦЕ
ОСНОВНЕ ПОНЯТТЯ
МАТЕМАТИЧНОГО
АНАЛІЗУ.
ТЕРМІН “ФУНКЦІЯ”
ВПЕРШЕ
ЗАПРОПОНУВАВ
ГОТФРІД ВІЛЬГЕЛЬМ
ЛЕЙБНІЦ У ХVІІ
СТОРІЧЧІ.

3.

ВЕЛИКИЙ ВНЕСОК У РОЗВИТОК І
РОЗШИРЕННЯ ПОНЯТТЯ “ФУНКЦІЯ”
ЗРОБИЛИ ВИДАТНІ ВЧЕНІ
Й.БЕРНУЛЛІ
М.І.ЛОБАЧЕВСЬКИЙ
Л.ЕЙЛЕР

4.

ЗАЛЕЖНІСТЬ ЗМІННОЇ У ВІД
ЗМІННОЇ Х НАЗИВАЮТЬ ФУНКЦІЄЮ,
ЯКЩО КОЖНОМУ ЗНАЧЕННЮ Х
ВІДПОВІДАЄ ЄДИНЕ ЗНАЧЕННЯ У.
Х - НЕЗАЛЕЖНА ЗМІННА
(АРГУМЕНТ),
У – ЗАЛЕЖНА ЗМІННА (ФУНКЦІЯ).

5.

Способи
задання
функції

6.

1)“ЗАДАНО ТАКУ ЗАЛЕЖНІСТЬ ЗМІННОЇ У ВІД ЗМІННОЇ Х,
ПРИ ЯКІЙ КОЖНОМУ ЗНАЧЕННЮ У ПОСТАВЛЕНО У
ВІДПОВІДНІСТЬ ПОДВОЄНЕ ЗНАЧЕННЯ Х.”
ЦЕ ОПИСОВИЙ СПОСІБ ЗАДАННЯ ФУНКЦІЇ.
2) У = 2 ∙ Х
ЦЕ СПОСІБ ЗАДАННЯ ФУНКЦІЇ ФОРМУЛОЮ.
3)
х
у
-2
-4
-1
-2
0
0
1
2
2
4
3
6
ЦЕ ТАБЛИЧНИЙ СПОСІБ ЗАДАННЯ ФУНКЦІЇ.

7.

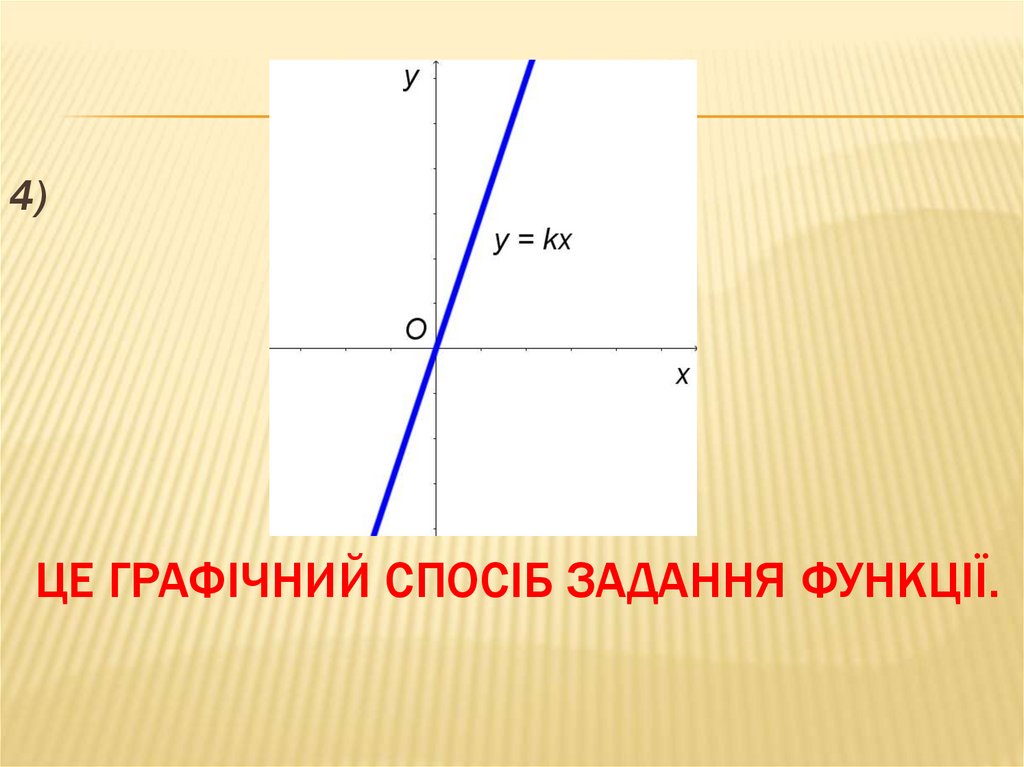
4)
ЦЕ ГРАФІЧНИЙ СПОСІБ ЗАДАННЯ ФУНКЦІЇ.

8.

Область
визначення
функції

9.

ОБЛАСТЬ ВИЗНАЧЕННЯ ФУНКЦІЇ – ЦЕ
МНОЖИНА ЗНАЧЕНЬ, ЯКИХ МОЖЕ
НАБУВАТИ АРГУМЕНТ Х
ПОЗНАЧАЄТЬСЯ D(f)

10.

ЗВЕРНІТЬ УВАГУ НА ОСОБЛИВІ ВИПАДКИ!
1) ІРРАЦІОНАЛЬНА ФУНКЦІЯ
y
f(x)
О.В. : f(x) ≥ 0
f(x)
2) ДРОБОВО-РАЦІОНАЛЬНА ФУНКЦІЯ y
g(x)
О.В. : g(x) ≠ 0
f(x)
3) ДРОБОВО-ІРРАЦІОНАЛЬНА y
g(x)
ФУНКЦІЯ
О.В. : g(x) > 0

11.

Область
значень
функції

12.

ОБЛАСТЬ ЗНАЧЕНЬ ФУНКЦІЇ – ЦЕ
МНОЖИНА ЗНАЧЕНЬ ЗАЛЕЖНОЇ ЗМІННОЇ
У, ЯКИХ ВОНА НАБУВАЄ ПРИ ВСІХ Х З
ОБЛАСТІ ВИЗНАЧЕННЯ
ПОЗНАЧАЄТЬСЯ Е(f)

13.

ЗВЕРНІТЬ УВАГУ НА ОСОБЛИВІ ВИПАДКИ!
1) ІРРАЦІОНАЛЬНА ФУНКЦІЯ
О.З. :
y
f(x)
у≥0
k
2) ДРОБОВО-РАЦІОНАЛЬНА ФУНКЦІЯ y
f(x)
О.З. : у ≠ 0
3) КВАДРАИЧНА ФУНКЦІЯ
О.З. : у ≥ 0
y ах
2

14.

ЗВЕРНІТЬ УВАГУ НА ОСОБЛИВІ ВИПАДКИ!
4) МОДУЛЬ ФУНКЦІЇ
О.З. :
y f(x)
у≥0

15.

Графік функції

16.

ГРАФІК ФУНКЦІЇ – ЦЕ
МНОЖИНА УСІХ ТОЧОК З
КООРДИНАТАМИ ( х; у )
КООРДИНАТНОЇ ПЛОЩИНИ,
ЯКІ ЗАДОВОЛЬНЯЮТЬ
РІВНЯННЯ ФУНКЦІЇ у = f(x)

17.

18.

Нулі
функції

19.

Нулі функції – це точки х, у яких
значення функції дорівнює 0,
тобто f(х) = 0.

20.

На графіку – це точки перетину
графіка з віссю абсцис.
a
b
c

21.

Парність
та непарність
функції

22.

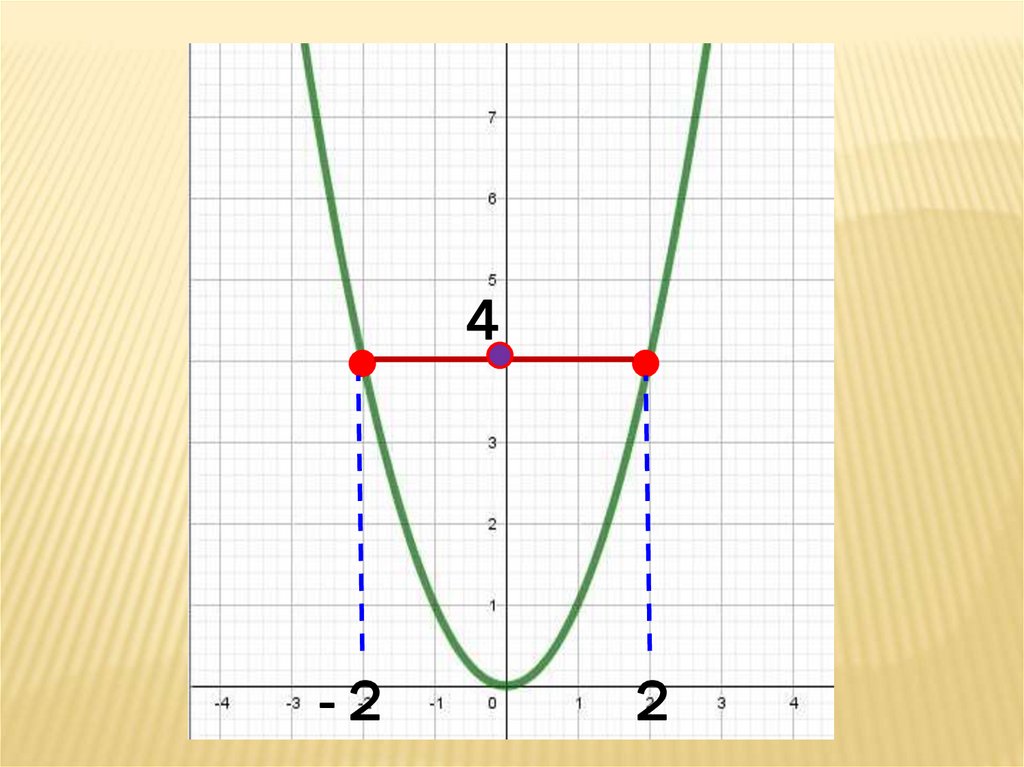
4
-2
2

23.

Протилежним аргументам
х = 2 та х = - 2
відповідає однакове
значення функції
у=4.
Така функція парна.

24.

4
-2
2
-4

25.

Протилежним аргументам
х = 2 та х = - 2
відповідають протилежні
значення функції
у = 4 та у = - 4.
Така функція непарна.

26.

Теорема 1.
ЯКЩО ДЛЯ АРГУМЕНТІВ
х = а ТА х = - а
ЗНАЧЕННЯ ФУНКЦІЇ
f(a) = f( - a),
ТО
ТАКА ФУНКЦІЯ ПАРНА.

27.

Теорема 2.
ЯКЩО ДЛЯ АРГУМЕНТІВ
х = а ТА х = - а
ЗНАЧЕННЯ ФУНКЦІЇ
f(a) = - f( - a),
ТО
ТАКА ФУНКЦІЯ НЕПАРНА.

28.

Зростання
та
спадання
функції

29.

7
2,8
2
12

30.

ЗНАЧЕННЮ
АРГУМЕНТА х = 2
ВІДПОВІДАЄ
ЗНАЧЕННЯ
ФУНКЦІЇ У = 2,8.
ЗНАЧЕННЮ
АРГУМЕНТА х = 12
ВІДПОВІДАЄ
ЗНАЧЕННЯ
ФУНКЦІЇ У = 7.
Тобто, більшому значенню
аргумента відповідає більше
значення функції.
Така функція зростаюча.

31.

4,7
0,8
1
6

32.

ЗНАЧЕННЮ
АРГУМЕНТА х = 1
ВІДПОВІДАЄ
ЗНАЧЕННЯ
ФУНКЦІЇ У = 4,7.
ЗНАЧЕННЮ
АРГУМЕНТА х = 6
ВІДПОВІДАЄ
ЗНАЧЕННЯ
ФУНКЦІЇ У = 0,8.
Тобто, більшому значенню
аргумента відповідає менше
значення функції.
Така функція спадна.

33.

Теорема 3.
ЯКЩО ДЛЯ АРГУМЕНТІВ
х = а ТА х = b
ТАКИХ, ЩО a < b ,
ЗНАЧЕННЯ ФУНКЦІЇ
f(a) < f(b),
ТО ТАКА ФУНКЦІЯ ЗРОСТАЄ.

34.

Теорема 4.
ЯКЩО ДЛЯ АРГУМЕНТІВ
х = а ТА х = b
ТАКИХ, ЩО a < b ,
ЗНАЧЕННЯ ФУНКЦІЇ
f(a) > f(b),
ТО ТАКА ФУНКЦІЯ СПАДАЄ.

35.

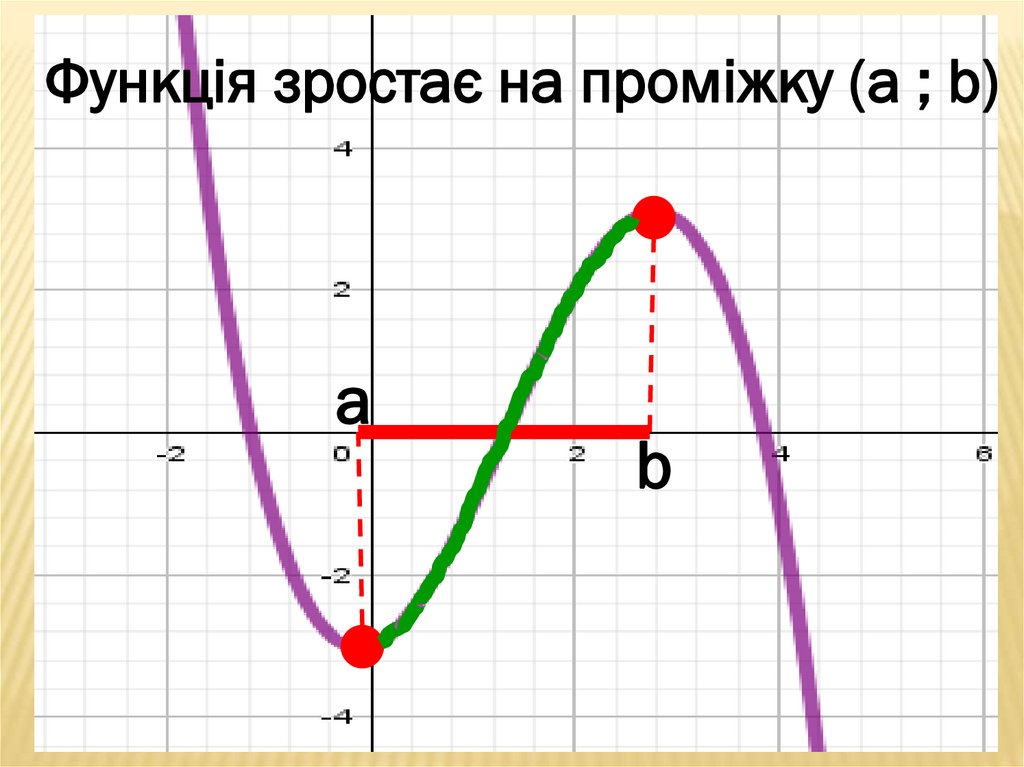
Функція зростає на проміжку (a ; b)
а
b

36.

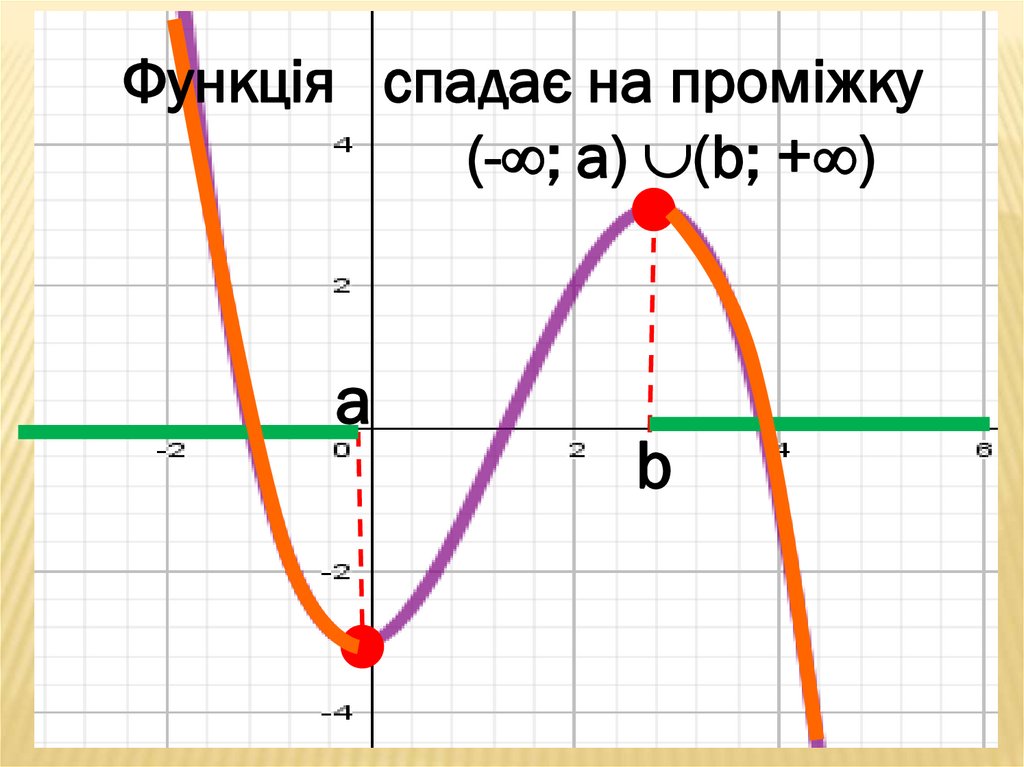
Функція cпадає на проміжку
(- ; а) (b; + )
а
b

37.

Знакосталість
функції

38.

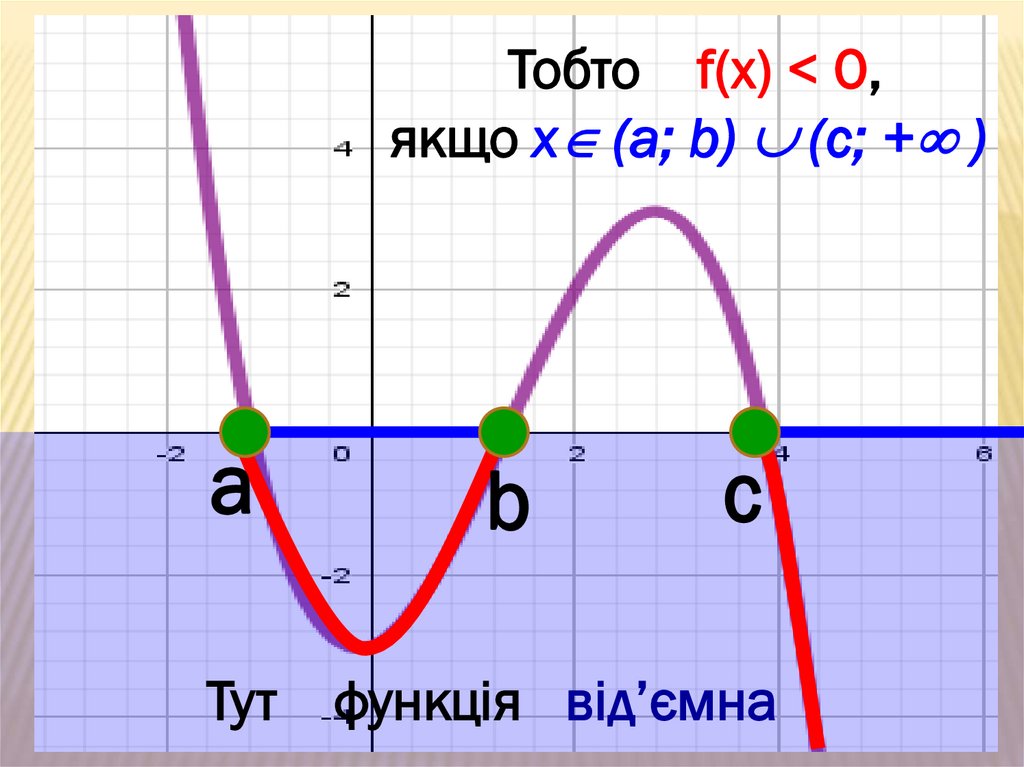
Тут функція додатна
a
b
c
Тобто f(x) > 0, якщо х ( - ; a) (b ; c )

39.

Тобто f(x) < 0,
якщо х (a; b) (c; + )
a
b
c
Тут функція від’ємна

40.

ДЯКУЮ ЗА УВАГУ!