Похожие презентации:
Функція та її властивості
1. Функція та її властивості
( повторення)2.
Що таке функція?Функцією називають
таку
залежність
змінної у від змінної
х,
при
якій
кожному значенню
х відповідає єдине
значення у
y f(x)
х - аргумент, незалежна
змінна
у - функція, залежна
змінна
3. Як можна задати функцію?
• З допомогою формули.• З допомогою таблиці
• З допомогою графіка
У = - 4х + 5
х
-2 -1 0
1
2
у
2
1
2
1
0
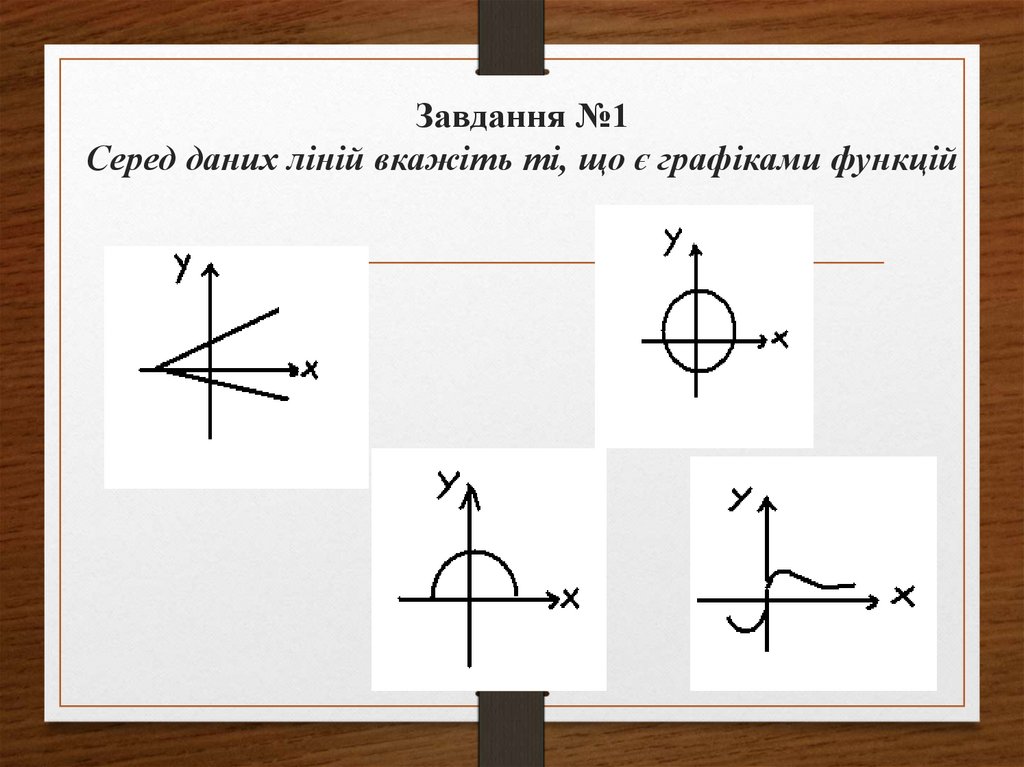
4. Завдання №1 Серед даних ліній вкажіть ті, що є графіками функцій
5.
Властивостіфункцій
6.
Область визначення – це всі значення змінної х при яких функціямає зміст.
Позначення D(f)
Вид функції
у = f(х), де f(х) многочлен
f ( x)
у
g ( x)
y
f (x)
у
f ( x)
g ( x)
Область
визначення
R або (-∞; ∞)
g(x)≠0
f(x)≥0
g(x)˃0
Область значень – це всі значення змінної у.
Позначення Е (f)
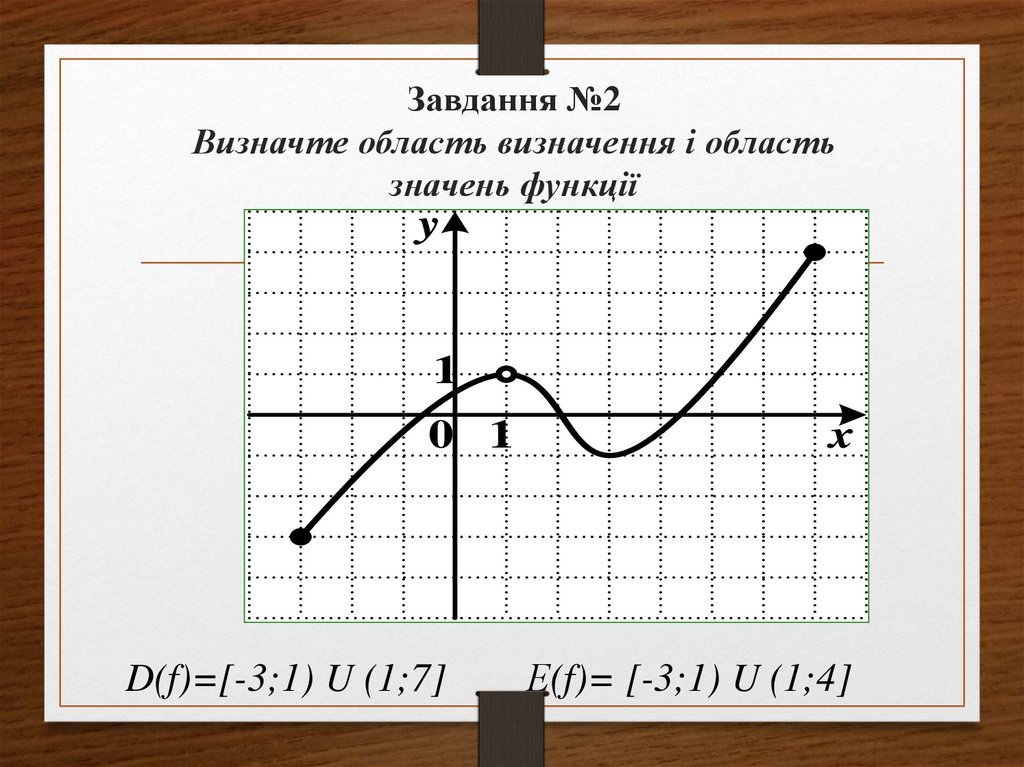
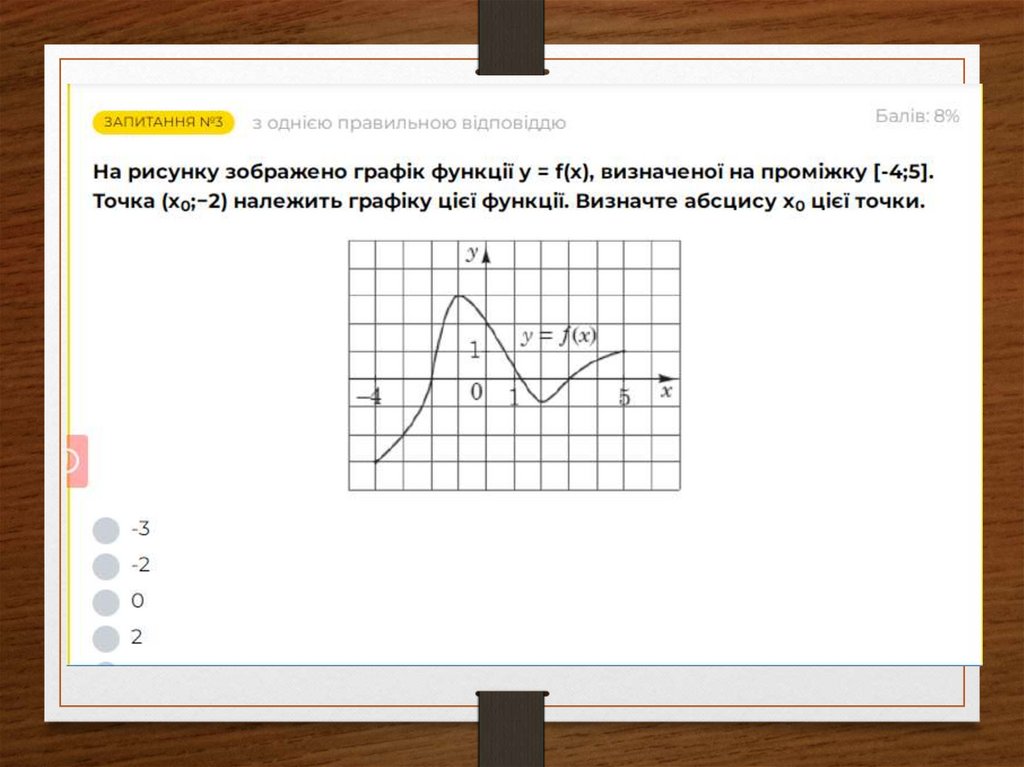
7. Завдання №2 Визначте область визначення і область значень функції
y1
0 1
D(f)=[-3;1) U (1;7]
x
Е(f)= [-3;1) U (1;4]
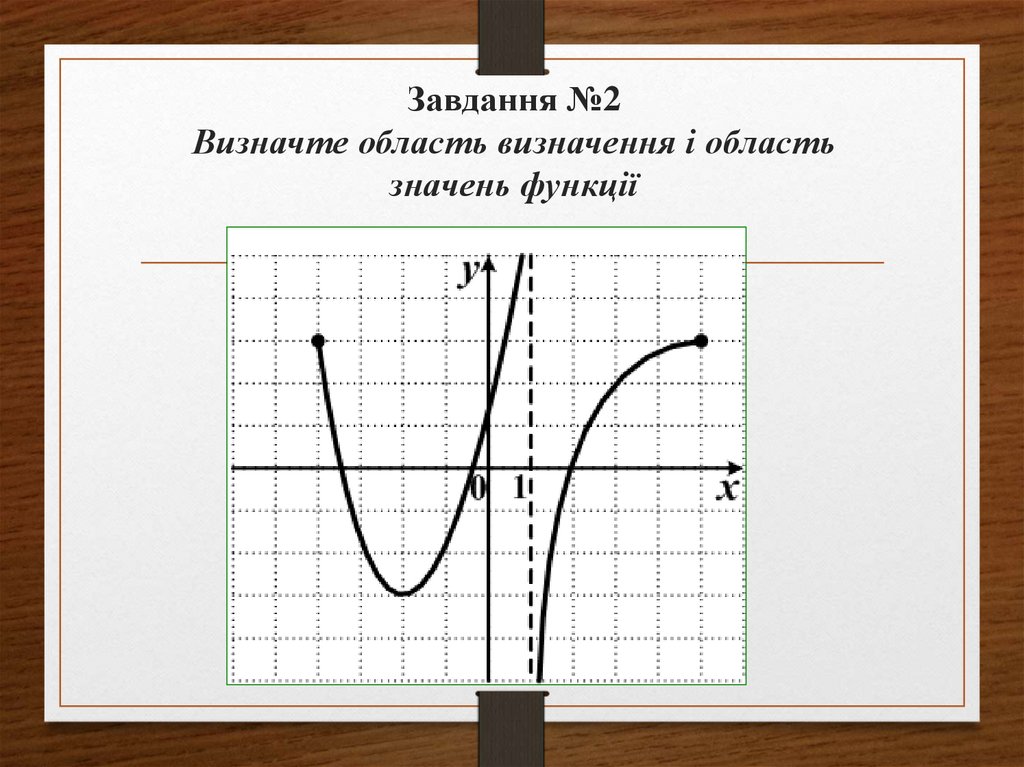
8. Завдання №2 Визначте область визначення і область значень функції
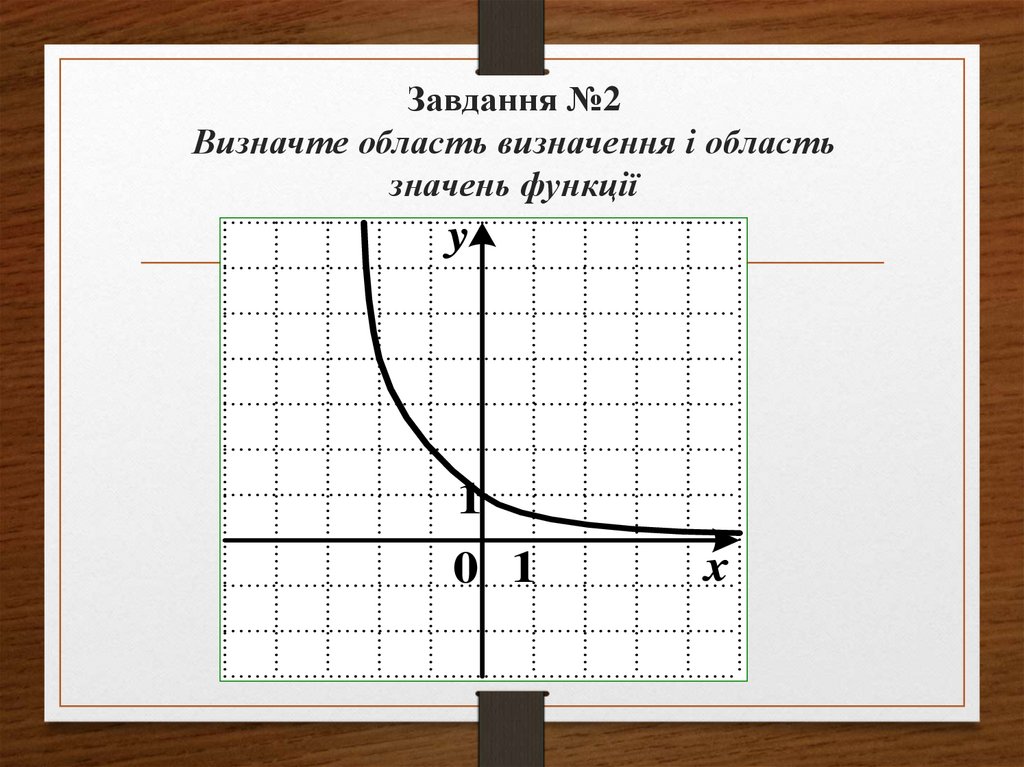
9. Завдання №2 Визначте область визначення і область значень функції
y1
0 1
x
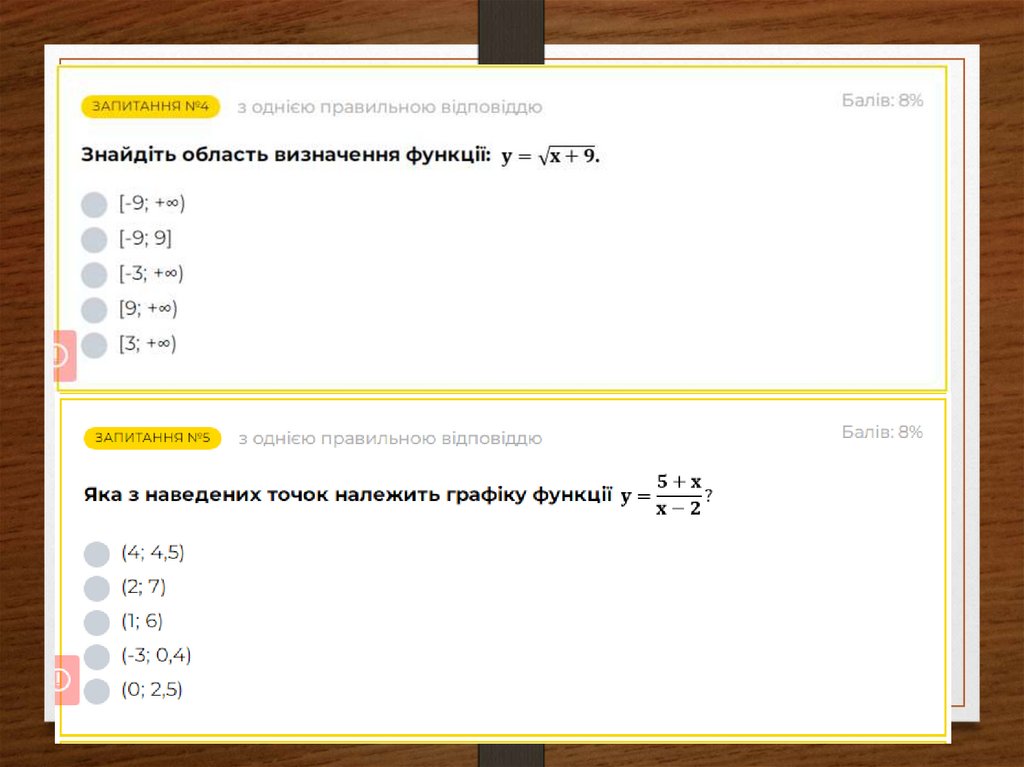
10. Завдання №3 Знайдіть область визначення функції
f ( x) x 6 x 92
5
f ( x)
( x 2)(5 x)
x 4
f ( x) 2
x 2
7
f ( x) 2
x 6x 9
f ( x) x 2
f ( x) x 5 x 2
x 2
f ( x)
x 2
11. Парність і непарність функції
1. Область визначення симетрична відносно початкукоординат
2. Виконується формула
f x f x
g x g x
парна функція
непарна функція
Якщо не виконується перша умова або друга, то
функція ні парна, ні непарна(індиферентна)
12.
Приклад №11) D(f)=R –
f(х)=х2+5
область визначення
симетрична відносно
початку координат
2) f(-х) = (-х)2+5=х2+5
f x f x
Отже,
Висновок: функція парна
13.
Приклад №25
f ( x)
x
1) D(f)=(-∞;0)U(0;∞) – область визначення
симетрична відносно початку координат
2)
f(-х) =
5
5 .
x
х
f x f x
Отже,
Висновок: функція не парна
14. Приклад №3
f ( x) x 5D(f)=[-5;∞) –
область визначення не
симетрична відносно початку координат
Приклад №4
1) D(f)=(-∞;5)U(5;∞) –
8
8
2) f ( x)
x 5
x 5
8
f ( x)
x 5
область визначення симетрична
відносно початку координат
f x f x
f x f x
Висновок: функція ні парна, ні непарна
15. Завдання №4 Визначте парність і не парність функції
а ) g ( x) 3 x x4
х
б) у 2
3х
5
1
в ) f ( x) х 3
х
7
2
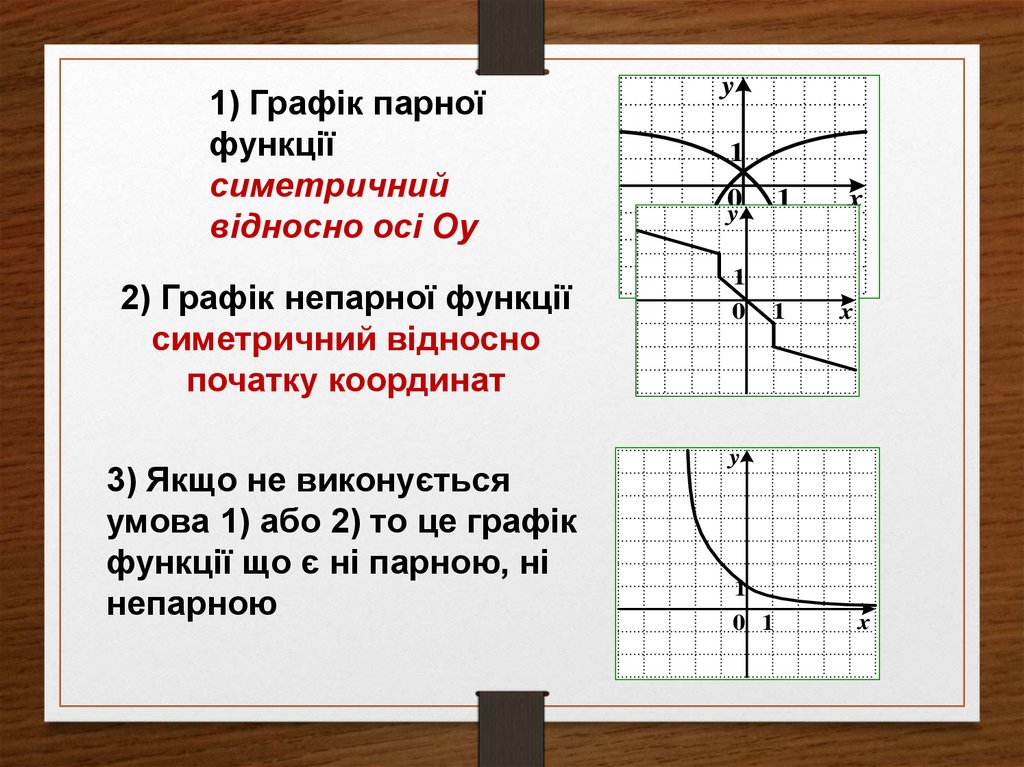
16.
1) Графік парноїфункції
симетричний
відносно осі Оу
y
0
1
x
2) Графік непарної функції
симетричний відносно
початку координат
1
0
1
x
3) Якщо не виконується
умова 1) або 2) то це графік
функції що є ні парною, ні
непарною
1
y
y
1
0 1
x
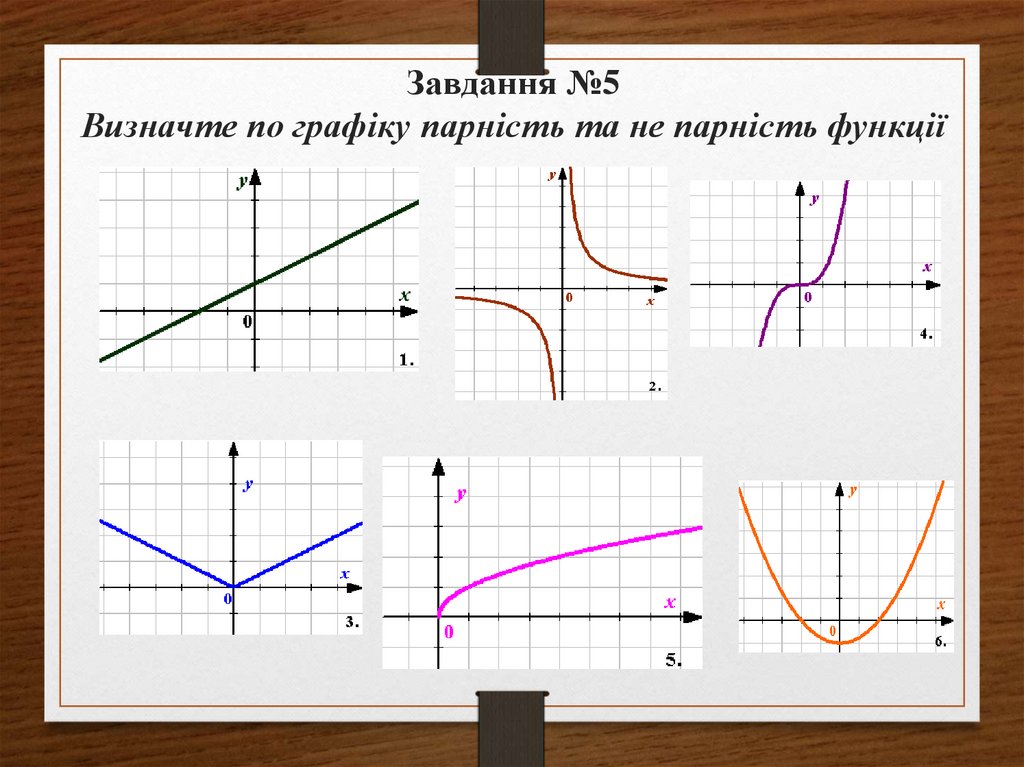
17. Завдання №5 Визначте по графіку парність та не парність функції
18.
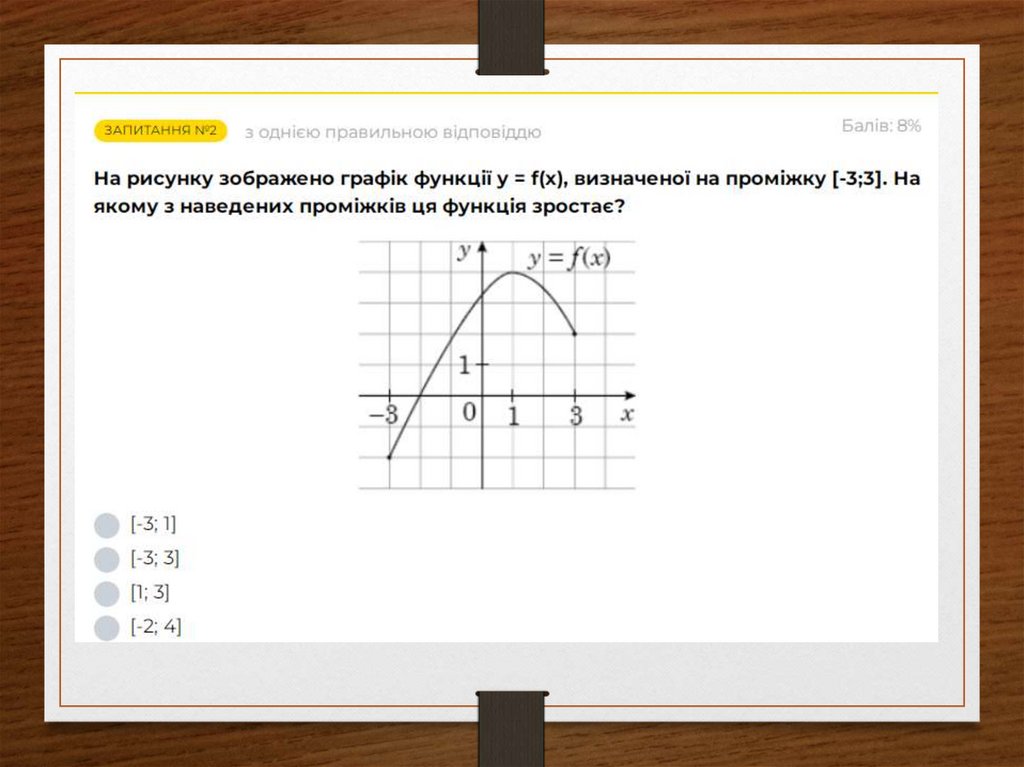
Монотонність(зростання та
спадання) функції
19.
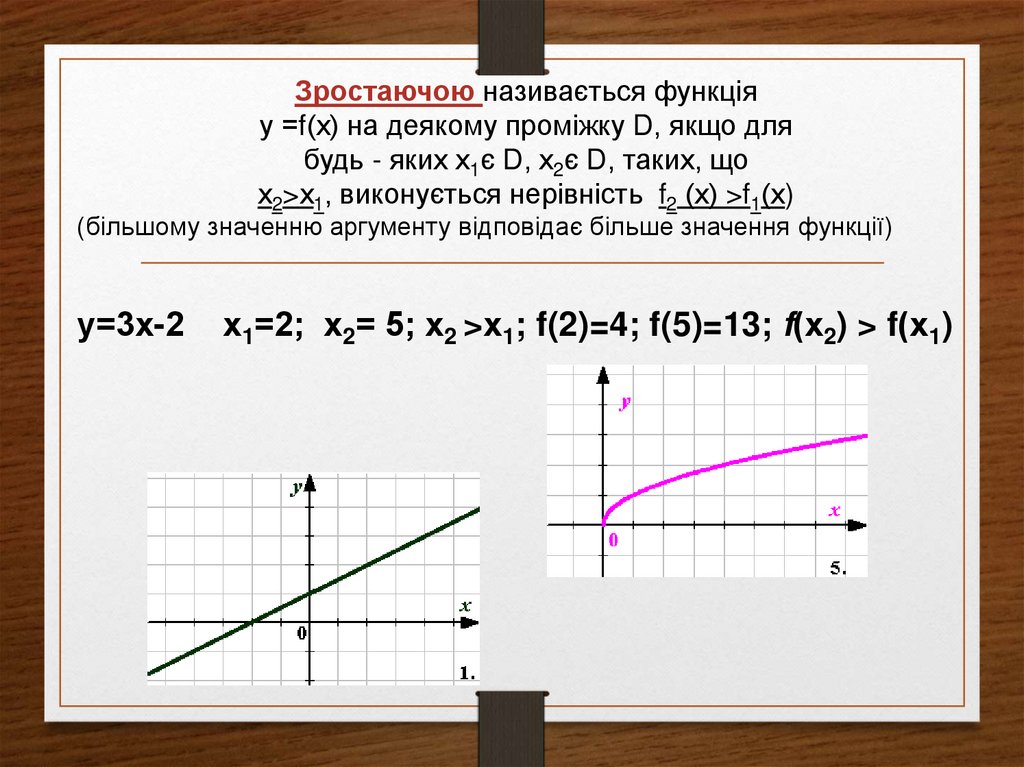
Зростаючою називається функціяу =f(х) на деякому проміжку D, якщо для
будь - яких х1є D, х2є D, таких, що
х2>х1, виконується нерівність f2 (х) >f1(х)
(більшому значенню аргументу відповідає більше значення функції)
у=3х-2
х1=2; х2= 5; х2 >х1; f(2)=4; f(5)=13; f(х2) > f(х1)
20.
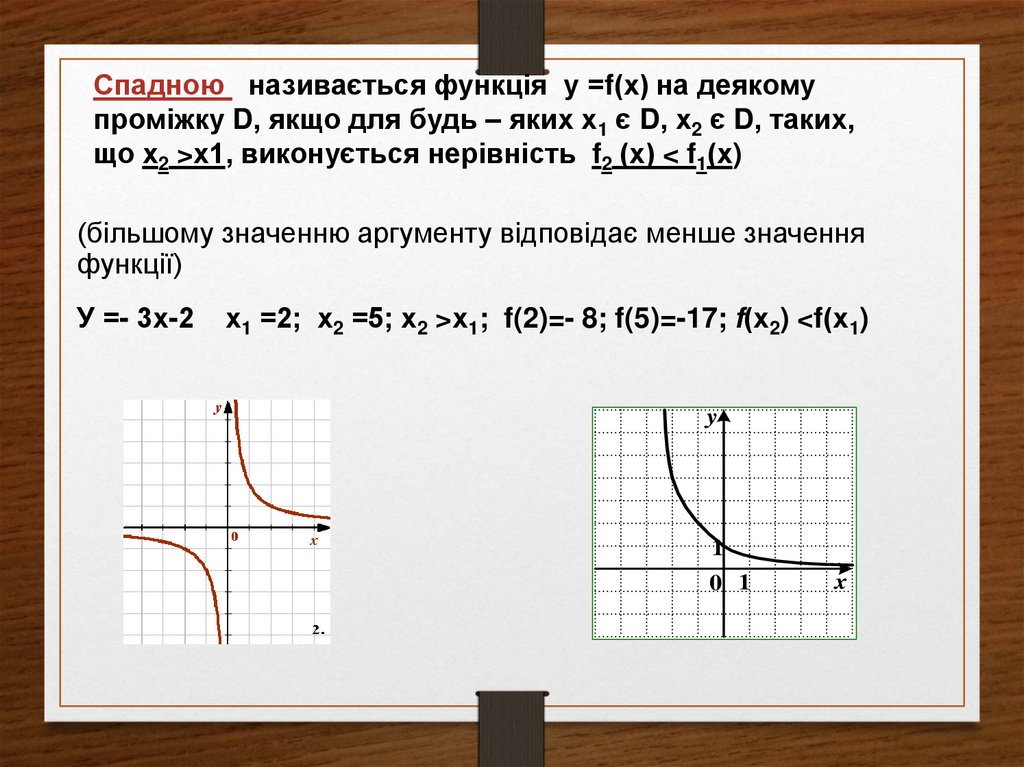
Спадною називається функція у =f(х) на деякомупроміжку D, якщо для будь – яких х1 є D, х2 є D, таких,
що х2 >х1, виконується нерівність f2 (х) < f1(х)
(більшому значенню аргументу відповідає менше значення
функції)
У =- 3х-2
х1 =2; х2 =5; х2 >х1; f(2)=- 8; f(5)=-17; f(х2) <f(х1)
y
1
0 1
x
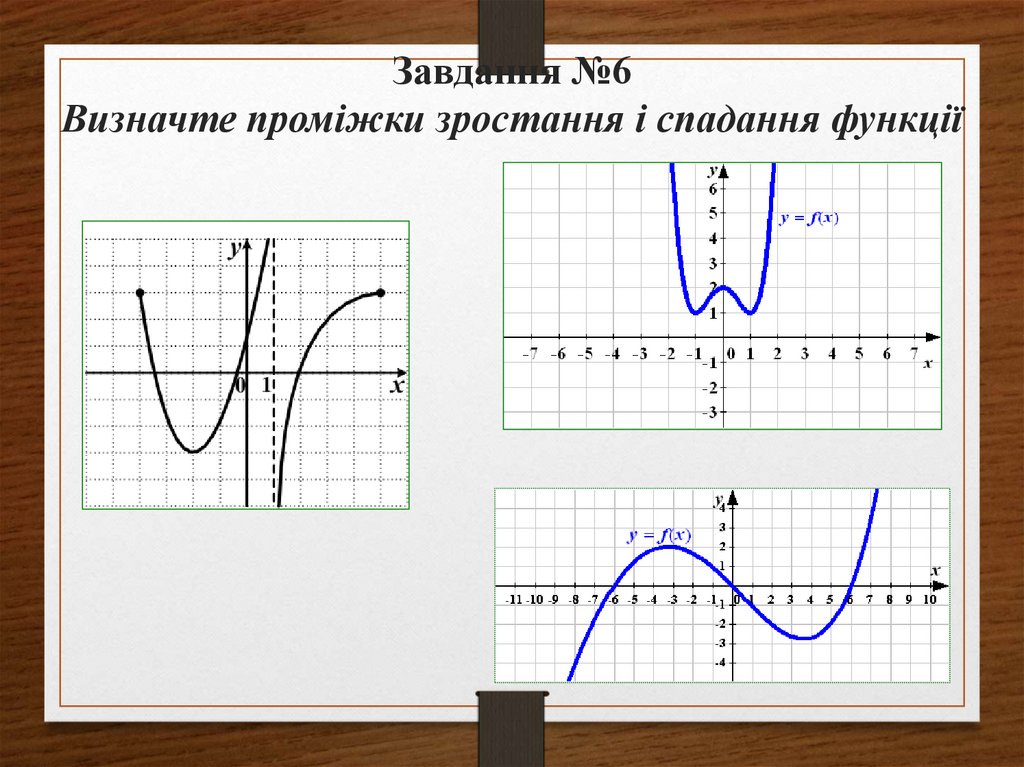
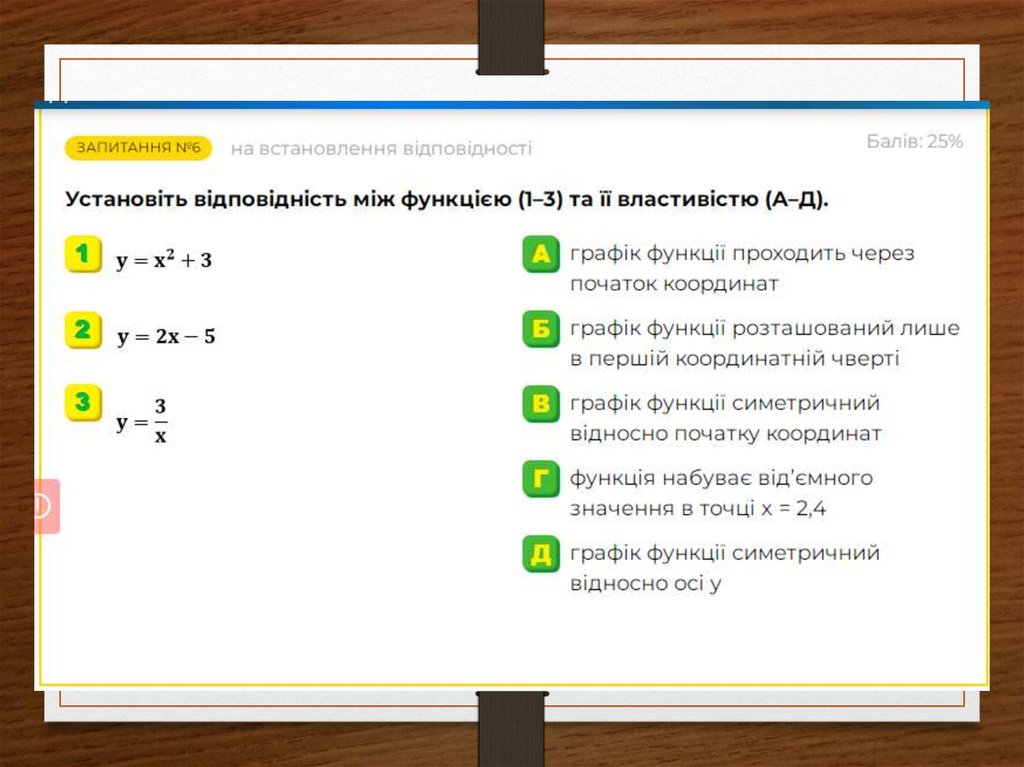
21. Завдання №6 Визначте проміжки зростання і спадання функції
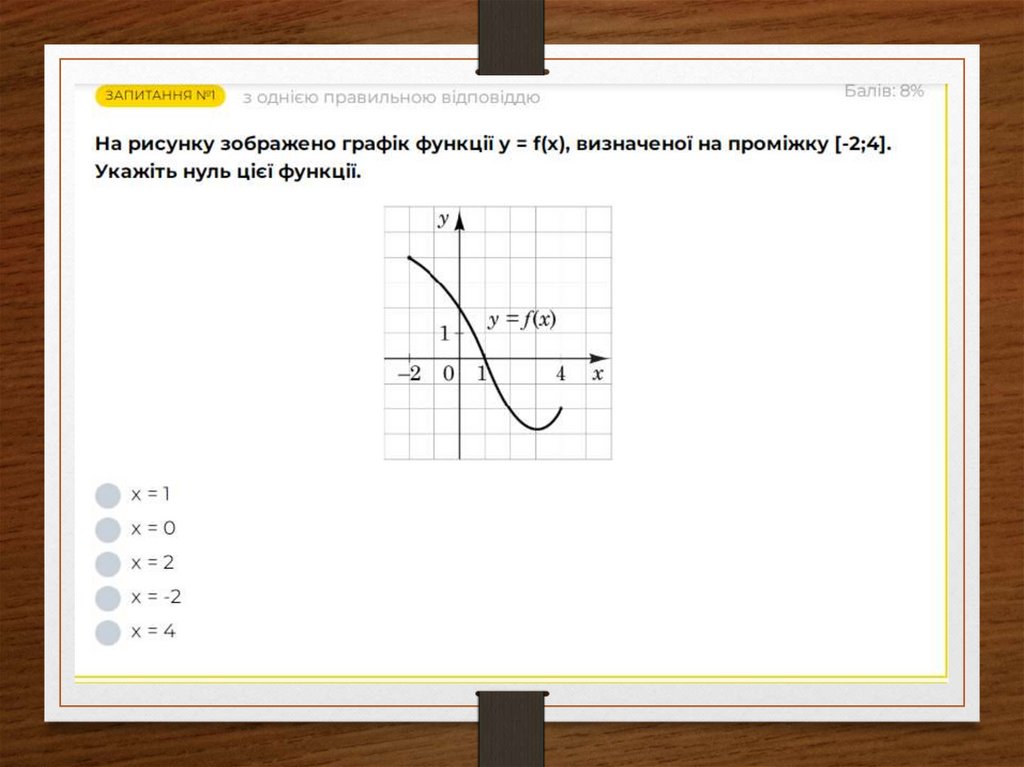
22. Нулі функції
Значення х при яких функція дорівнює нулю.Щоб знайти нулі функції потрібно функцію прирівняти
до нуля і розв'язати рівняння.
у=4х-8; 4х-8=0; 4х=8; х=2-нуль функції
По графіку нулі функції – це точки перетину графіка з
віссю Ох
23.
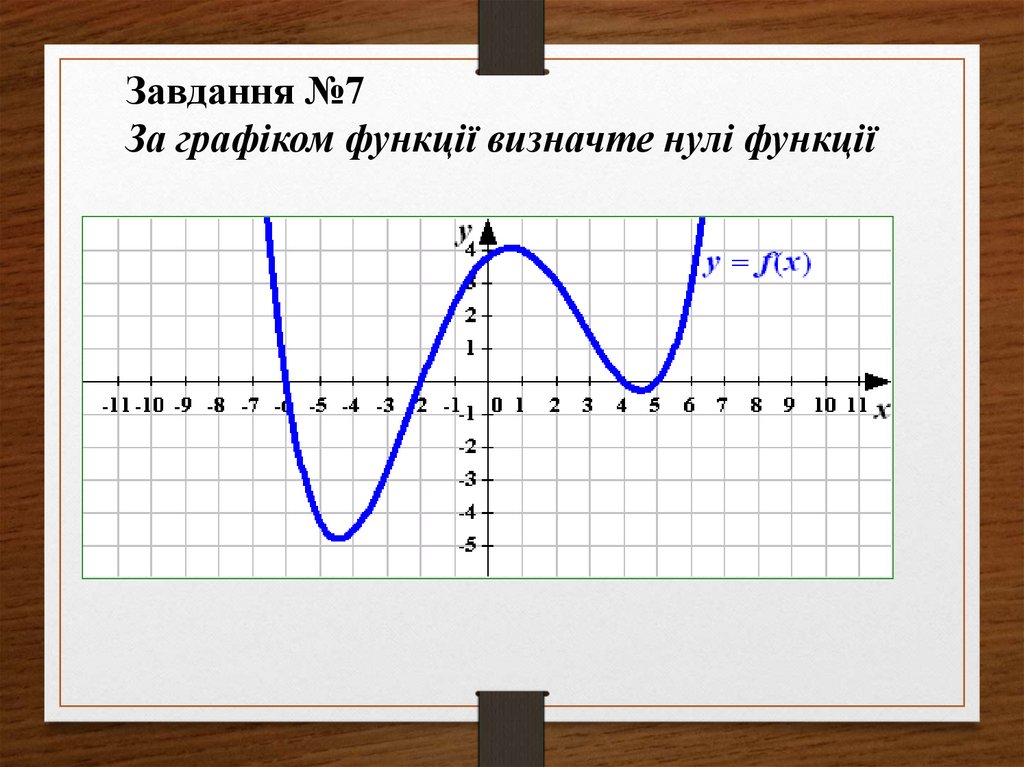
Завдання №7За графіком функції визначте нулі функції
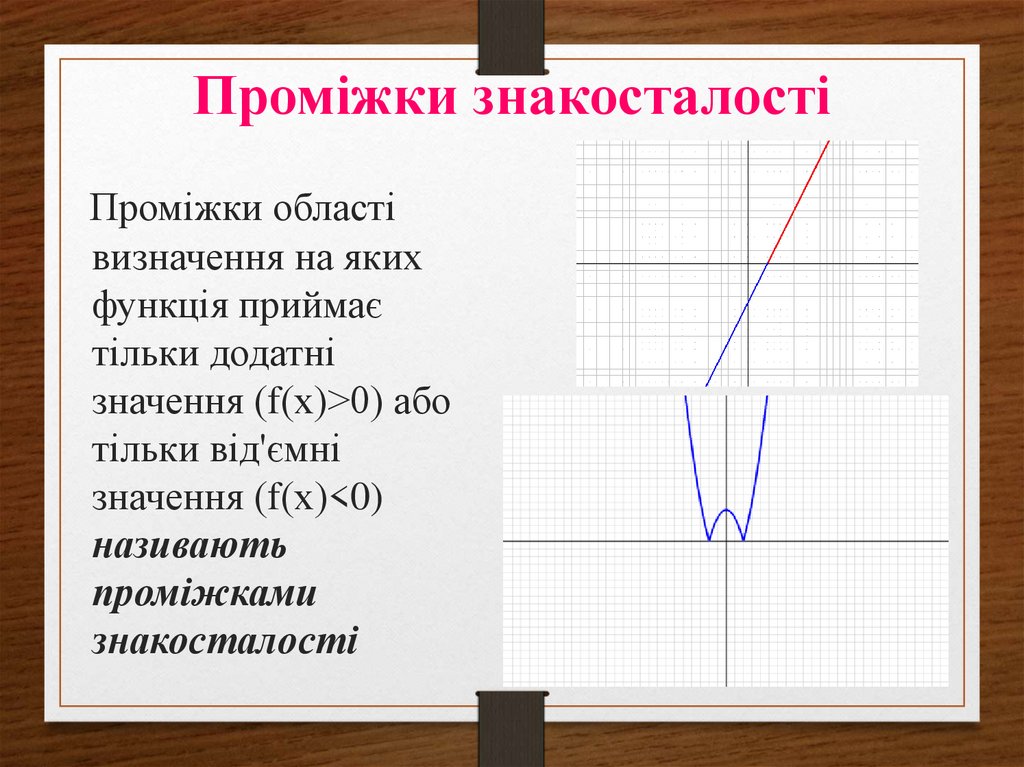
24. Проміжки знакосталості
Проміжки областівизначення на яких
функція приймає
тільки додатні
значення (f(х)˃0) або
тільки від'ємні
значення (f(х)<0)
називають
проміжками
знакосталості
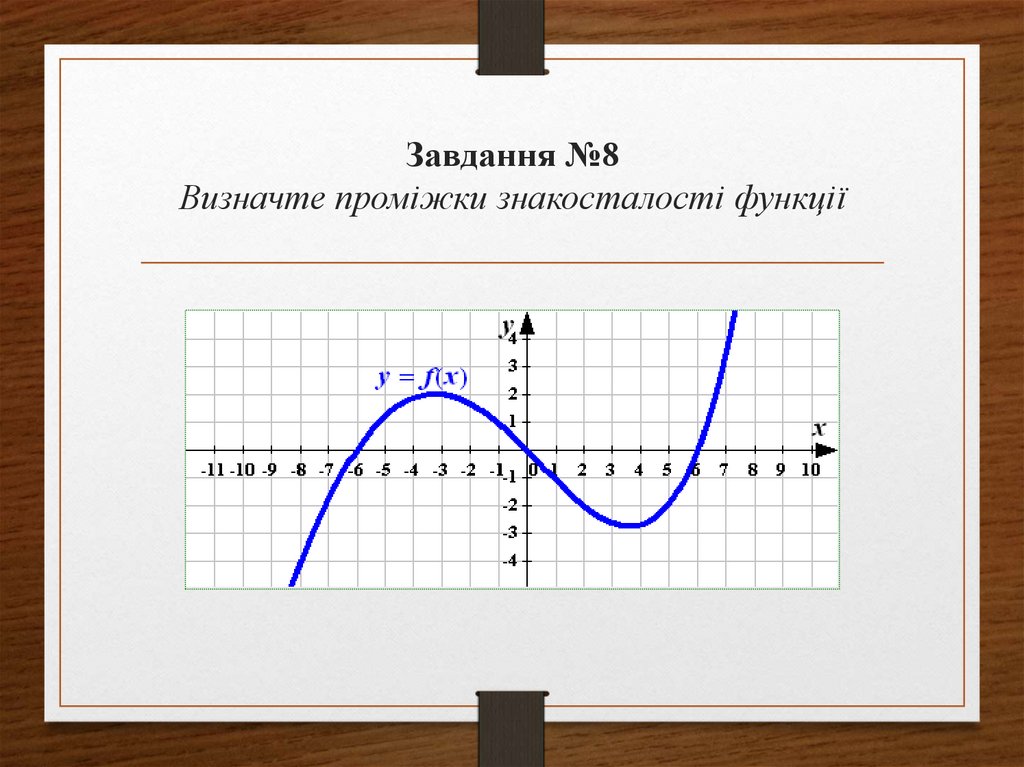
25. Завдання №8 Визначте проміжки знакосталості функції
26. Дослідити функцію - це виявити її властивості
1.2.
3.
4.
5.
6.
7.
Область визначення
Область значень
Парність(не парність)
Нулі функції
Проміжки знакосталості
Проміжки монотонності
Перетин з віссю Ох, з віссю Оу
27.
Основні видифункцій
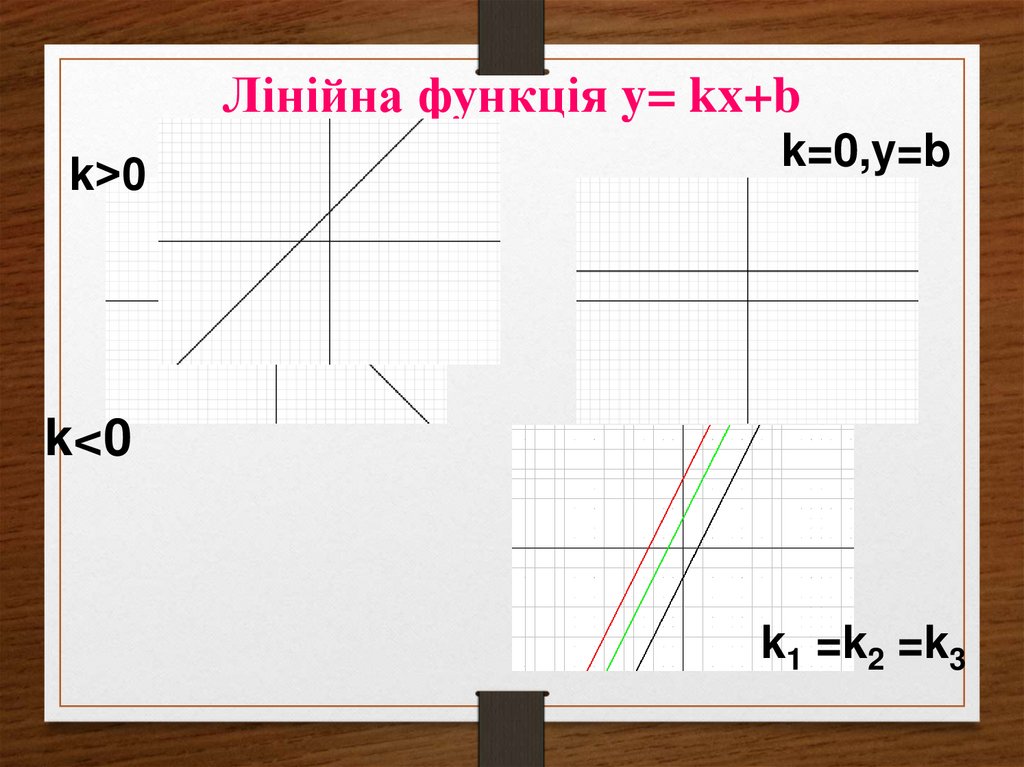
28. Лінійна функція y= kx+b
k˃0k=0,y=b
k<0
k1 =k2 =k3
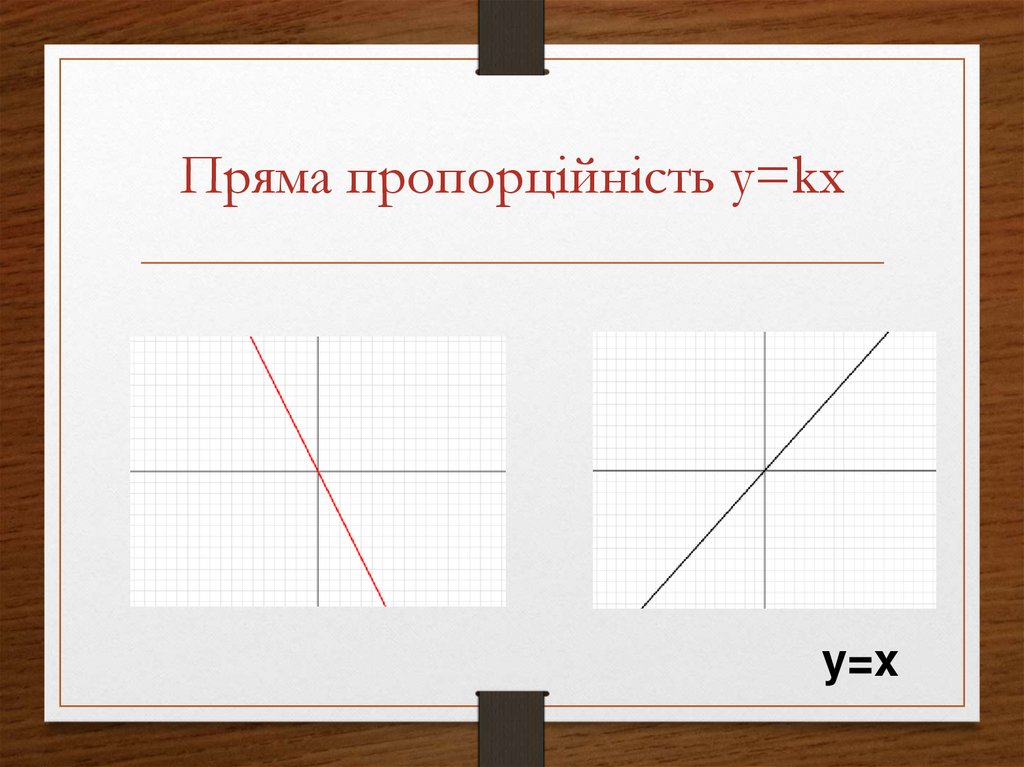
29. Пряма пропорційність y=kx
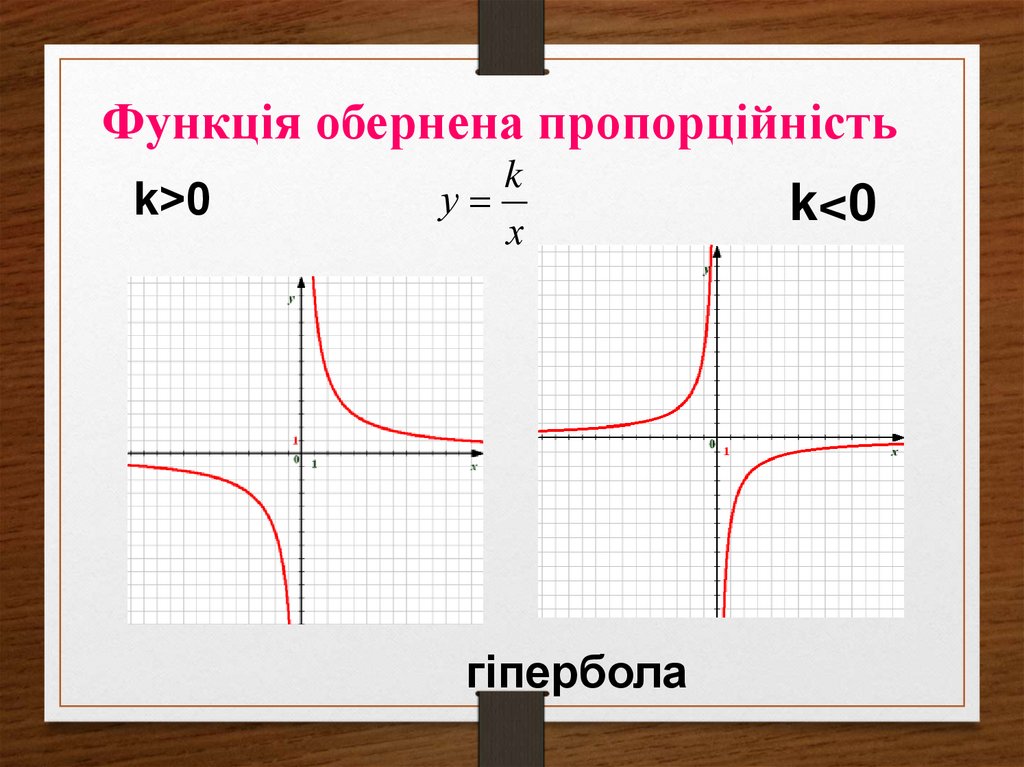
y=x30. Функція обернена пропорційність
k˃0k
у
х
гіпербола
k<0
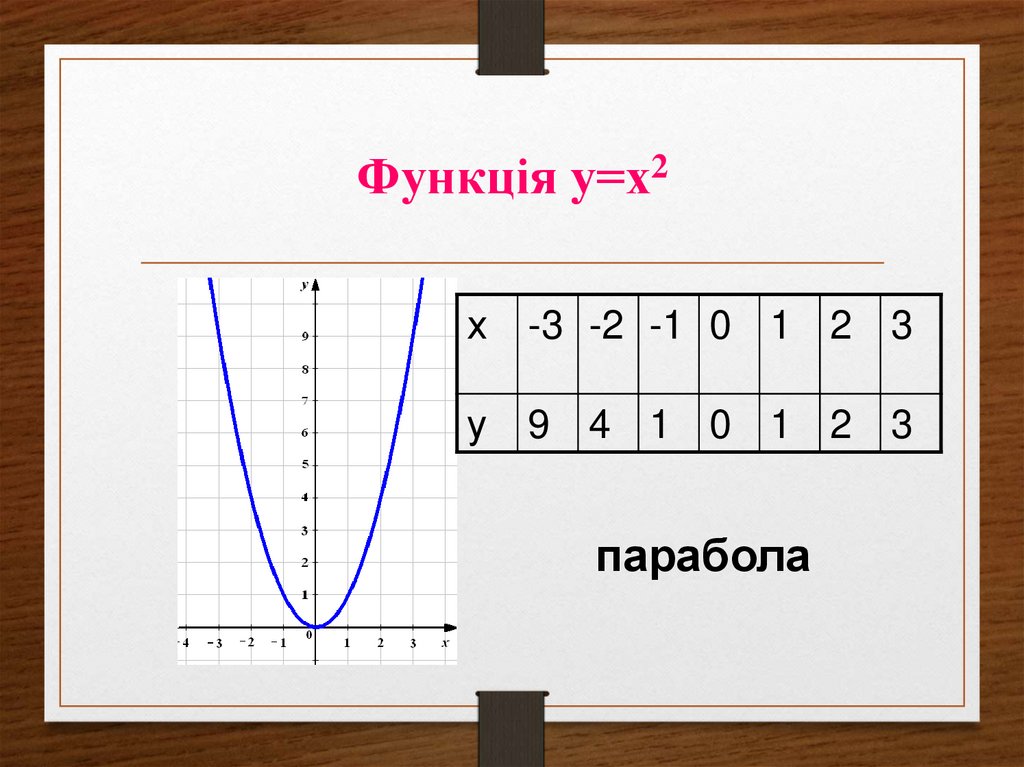
31. Функція у=х2
х-3 -2 -1 0 1 2 3
у
9 4 1 0 1 2 3
парабола
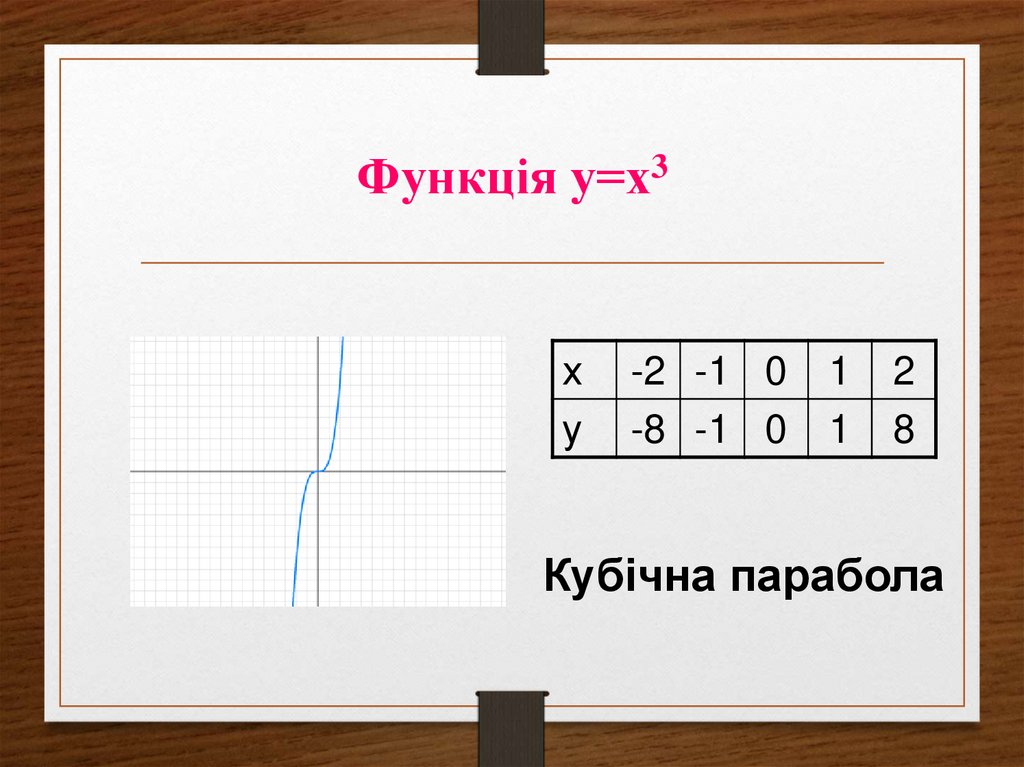
32. Функція у=х3
ху
-2 -1 0
-8 -1 0
1
1
2
8
Кубічна парабола
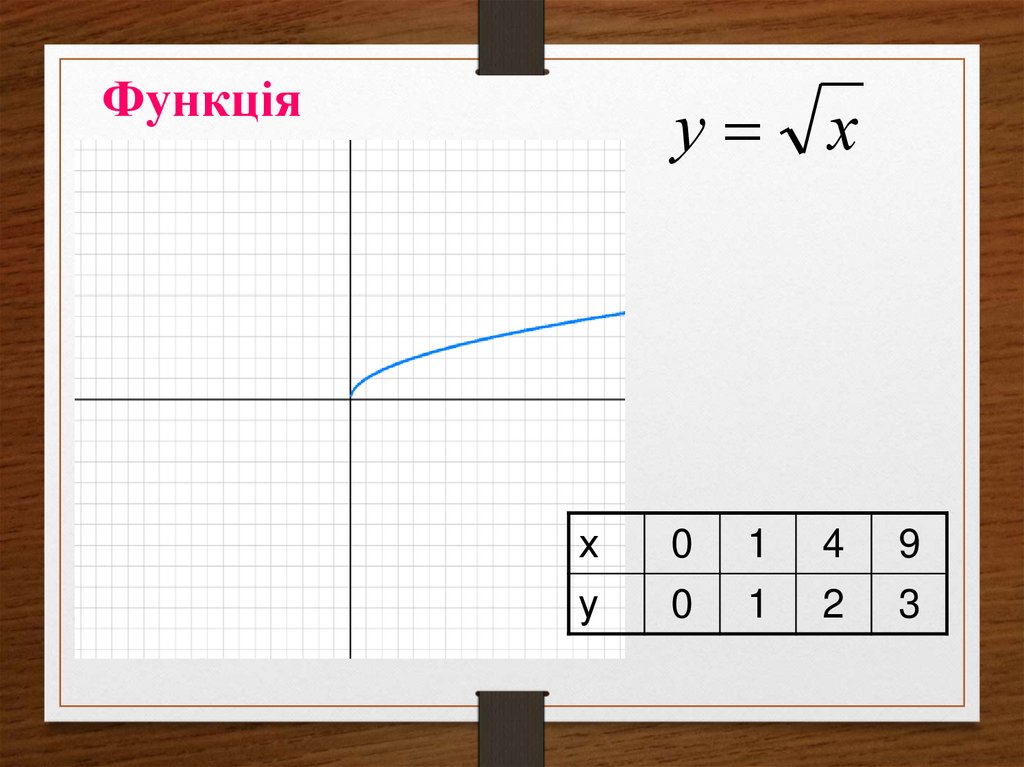
33. Функція
у хх
0
1
4
9
у
0
1
2
3
34. Функція у =│Х│
35.
Перетворенняграфіків
функцій
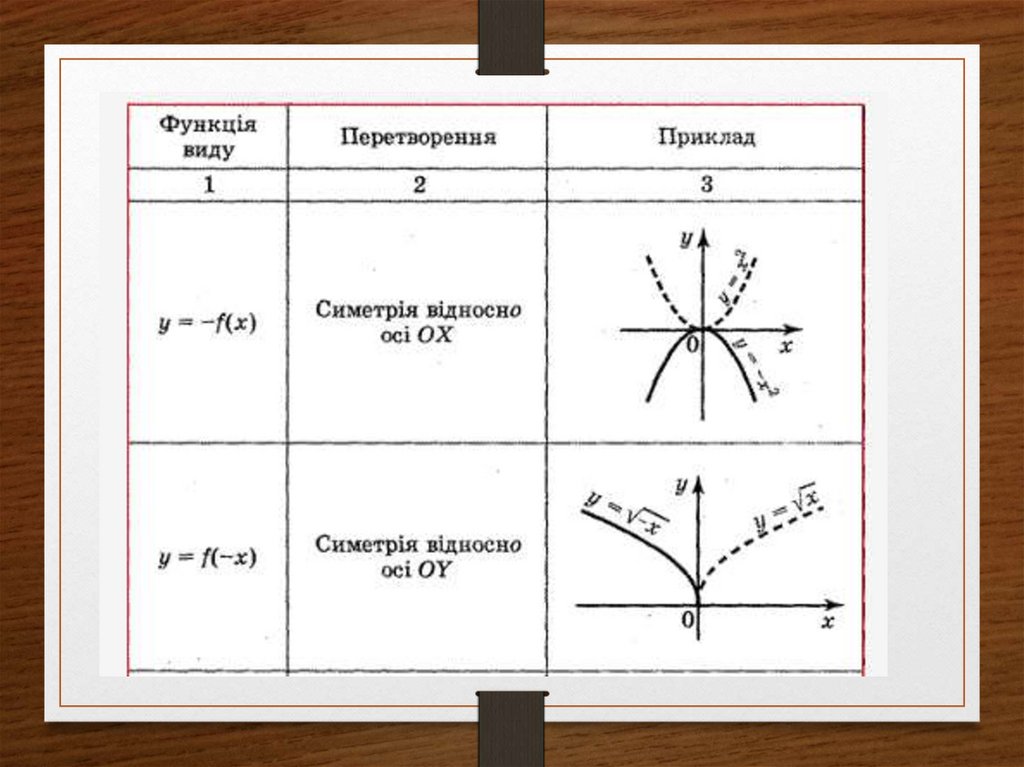
36.
37.
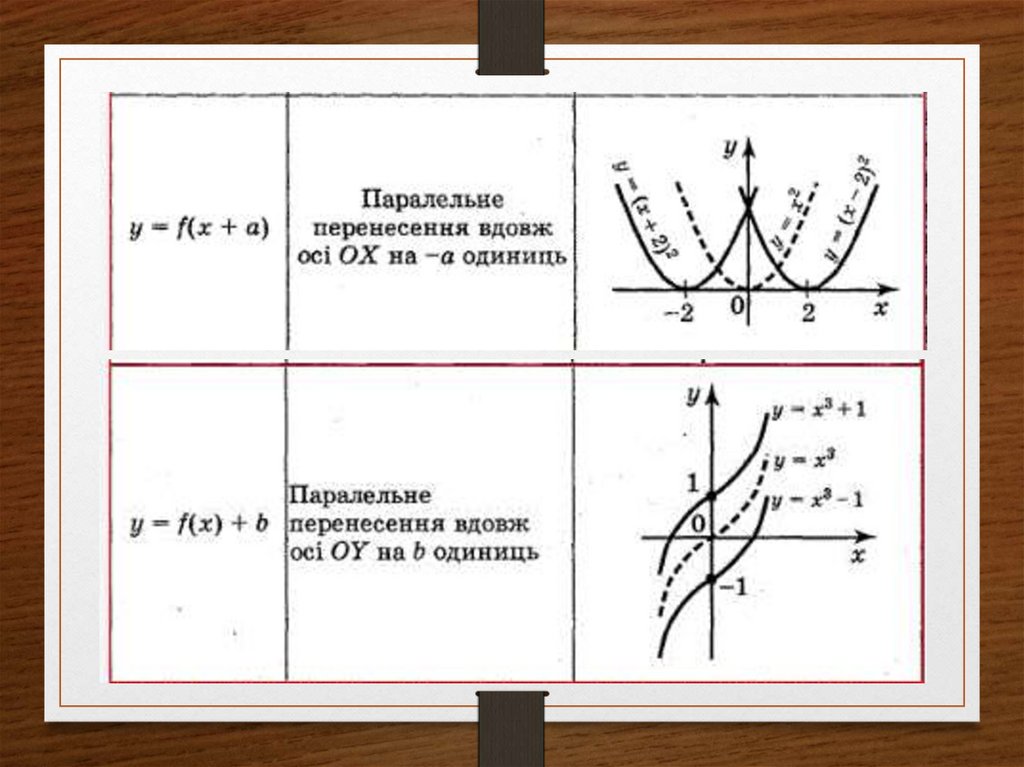
38.
39.
40.
Завдання №10Побудуйте графік функції та дослідіть
його властивості
1
х
9) у
1) у
3
5) у х
3х
3
3 6) у х 3 10) у 5 х
2) у
х
3
11
)
у
7
)
у
2
х
3
3) у х 3
х
4) у 3 х
8) у 2 х 3
х
12) у
3
41.
Готуємосьдо НМТ
























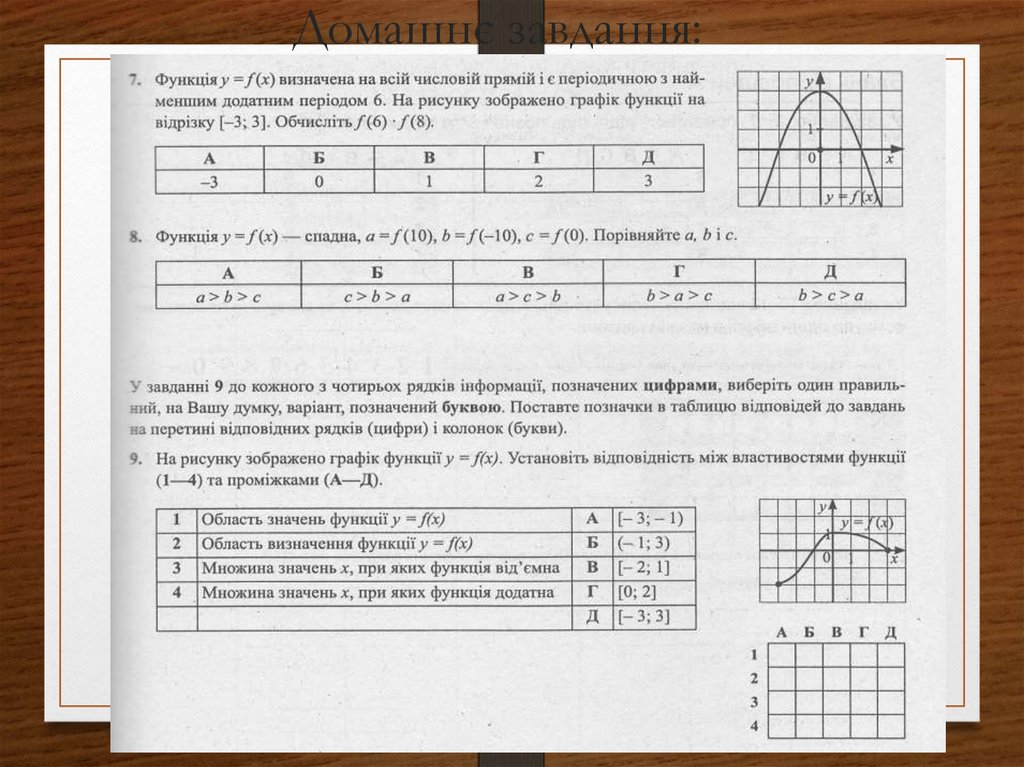
 Математика
Математика








