Похожие презентации:
Золотое сечение вокруг нас
1.
Работу выполнил:Ремезов Руслан Александрович,
обучающийся 9 класса
2.
Цель проекта – выявить «золотое сечение» в математике,природе, архитектуре, искусстве.
Задачи:
1. Изучить понятия «пропорция»; «золотое сечение».
2. Исследовать присутствие золотого сечения в различных
областях жизни человека.
3. Научиться анализировать и делать выводы.
Предметы исследования: математика, искусство, живопись,
архитектура, природа.
3.
АС : АВ = СВ : АС, получается верная пропорция.Это отношение и названо золотым сечением.
Золотое сечение - это такое деление отрезка на неравные части, при
котором длина его большей части так относится к длине всего
отрезка, как длина меньшей части к большей.
Или обратное отношение:
меньший отрезок так относится к большему, как больший ко всему.
Это отношение приближенно равно 5/8 или 0,618…
Обратное отношение приближенно равно 1,6180339887…
4.
ПифагорЛе Корбюзье
Леонардо Фибоначчи
Леонардо да Винчи
Евклид
5.
Объекты животного и растительного мираЖивопись
Архитектура
Музыкальные произведения
Поэзия
Бытовые предметы
Физические параметры внешней среды (громкость звука, влажность воздуха,
давление воздуха
Объекты астрономии
Тело человека и его отдельные органы (включая биоритмы и функционирование
головного мозга и зрительного восприятия)
6.
Золотой прямоугольник - прямоугольник, отношение сторон которого равно φ:книги, открытки, плитки шоколада, монитор компьютера, экран телевизора,
бумажник и множество других предметов.
Если построить прямоугольник со
сторонами, соотношение которых
будет равно пропорции золотого
сечения, и вписать в него ещё
один «золотой прямоугольник», в
тот — ещё один, и так до
бесконечности внутрь и наружу,
то по угловым точкам
прямоугольников можно
провести спираль. Интересно то,
что такая спираль совпадёт со
срезом раковины наутилуса, а
также другими встречающимися
в природе спиралями
7.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.Особенность последовательности чисел состоит в том, что каждый ее член,
начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8
= 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда
приближается к отношению золотого деления.
Так, 21: 34 = 0,617, а 34: 55 = 0,618.
Это отношение обозначается символом φ.
Только это отношение - 0,618: 0,382 - дает непрерывное деление отрезка
прямой в золотой пропорции, увеличение его или уменьшение до
бесконечности, когда меньший отрезок так относится к большему, как
больший ко всему.
8.
Леонардо да Винчи. Картина "Джоконда".Композиция портрета построена на «золотых треугольниках».
9.
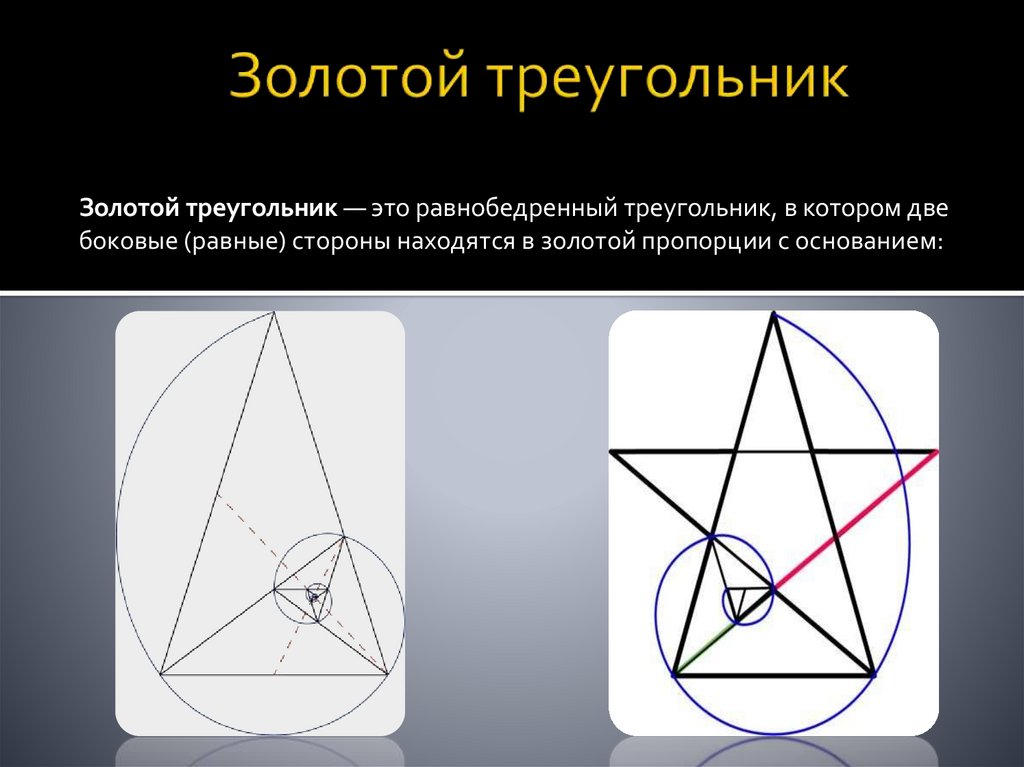
Золотой треугольник — это равнобедренный треугольник, в котором двебоковые (равные) стороны находятся в золотой пропорции с основанием:
10.
Парфенон (V в. до н. э.).11.
Храм,построенный
по
принципу золотого сечения. При
его высоте в 10 метров, высота
барабана с куполом будут равны
3,82 см, а высота основания
строения будет 6,18 см.











 Математика
Математика








