Численное интегрирование

1. Лабораторная №7. Численное интегрирование

2. Интегрирование

• Применения: при вычислении площадей и
объемов, значений работы, произведенной
некоторыми силами, и т.д.
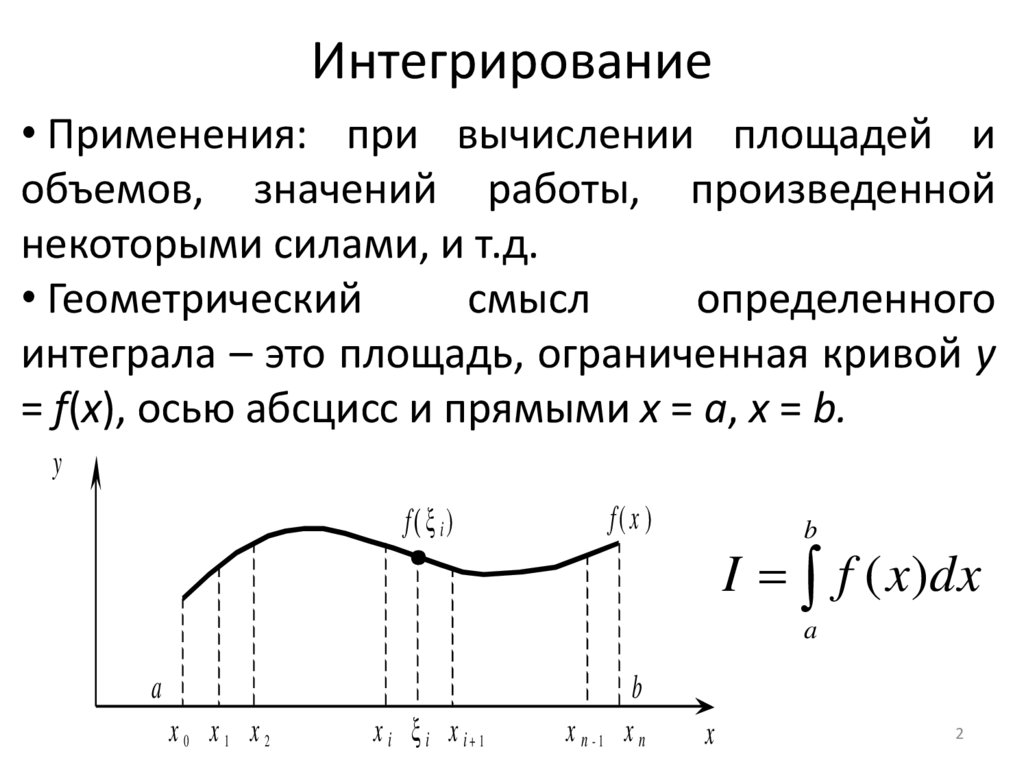
• Геометрический
смысл
определенного
интеграла – это площадь, ограниченная кривой y
= f(x), осью абсцисс и прямыми x = a, x = b.
y
f( ξ i )
f( x )
b
I f ( x)dx
a
a
x0 x1 x2
x i ξ i x i+ 1
b
x n -1 x n
x
2

3.

Для некоторых классов аналитически заданных
функций f(x), определенный интеграл можно
вычислить
непосредственно,
т.е.
найти
первообразную и воспользоваться формулой
Ньютона-Лейбница:
b
b
f ( x ) dx F ( x ) |a F (b) F ( a )
a
На практике это случается редко. Чаще всего:
а) не удается выразить первообразную F(x) через
элементарные функции, б) не всегда ответ
удобен для использования, в) иногда значения
f(x) заданы лишь в табличной форме.
3

4. Численный подход

Поэтому для решения поставленной задачи
приходится использовать методы численного
интегрирования, общая суть которых состоит в
замене подынтегральной функции на такую
аппроксимирующую функцию, чтобы интеграл от
нее можно было легко найти в элементарных
функциях.
Чаще
всего
в
качестве
аппроксимирующих функций берут некоторые
интерполяционные многочлены.
Основная идея численного интегрирования
заложена уже в известном определении
интеграла по Риману.
4

5. Интеграл по Риману

Пусть вещественная функция f(x) определена и
ограничена на интервале [a, b]. Разобьем его на
n произвольных частичных интервалов [xi, xi+1],
0 i n–1, x0 = a, xn = b. Выберем в каждом
частичном интервале произвольную точку ,
xi xi+1,
и
составим
так
называемую
интегральную сумму
y
f( ξ i )
f( x )
n 1
S f ( i )( xi 1 xi )
i 0
a
x0 x1 x2
x i ξ i x i+ 1
b
x n -1 x n
x
5

6.

Если предел S при стремлении длины
наибольшего частичного интервала к нулю
существует для произвольных i, то его называют
интегралом Римана от функции f(x):
I
lim S
max | x i 1 x i | 0
На практике нельзя взять бесконечно малые
длины отрезков. Но если взять их достаточно
малыми, то искомый интеграл можно
приблизительно
заменить
интегральной
суммой. По существу, в этом и состоит численное
интегрирование.
6

7. Формулы численного интегрирования

Существующие на практике формулы
численного интегрирования, по существу,
отличаются от интегральной суммы
только:
1) способами разбиения интервала, т.е.
выбором точек xi, i;
2) методами ускорения сходимости
суммы к точному значению;
3) оценкой погрешности.
7

8. Квадратурная формула

Представим интегральную сумму в более
общем виде. Заменим коэффициенты (xi+1
– xi) в ней некоторыми числами qi, не
зависящими от f(x). Тогда
n 1
S qi f ( i )
i 0
где точки a i b называются узлами
метода, а числа qi – весами узлов.
8

9.

Интеграл тогда следует записать в виде:
b
n 1
a
i 0
f ( x)dx qi f ( i ) R
Эта формула называется квадратурной
формулой, а R – погрешностью (остаточным
членом) квадратурной формулы.
Её смысл фактически состоит в замене
функции некоторым интерполяционным
многочленом.
9

10.

При
рассмотрении
конкретного
метода
численного интегрирования соответствующая
ему
квадратурная
формула
считается
заданной, если указано, как выбирать узлы i и
соответствующие веса qi, а также дана методика
оценки погрешности R для определенных
классов функций.
При реализации квадратурных формул в
подавляющем большинстве случаев используется
равномерная сетка с произвольным числом
интерполяционных узлов, что определяет
требования
к
степени
используемых
интерполяционных многочленов.
10

11.

Чтобы не иметь дело с многочленами высоких
степеней, обычно интервал интегрирования
разбивают на отдельные небольшие участки,
применяют рабочие формулы невысокого
порядка на каждом участке и потом
складывают результаты расчета и оценочные
погрешности.
Приведем
простейшие
квадратурные
формулы, сначала для отдельного малого
интервала [хi, xi+1], а затем для всего интервала
интегрирования [a, b] в виде так называемых
составных квадратурных формул.
11

12. Формула прямоугольников

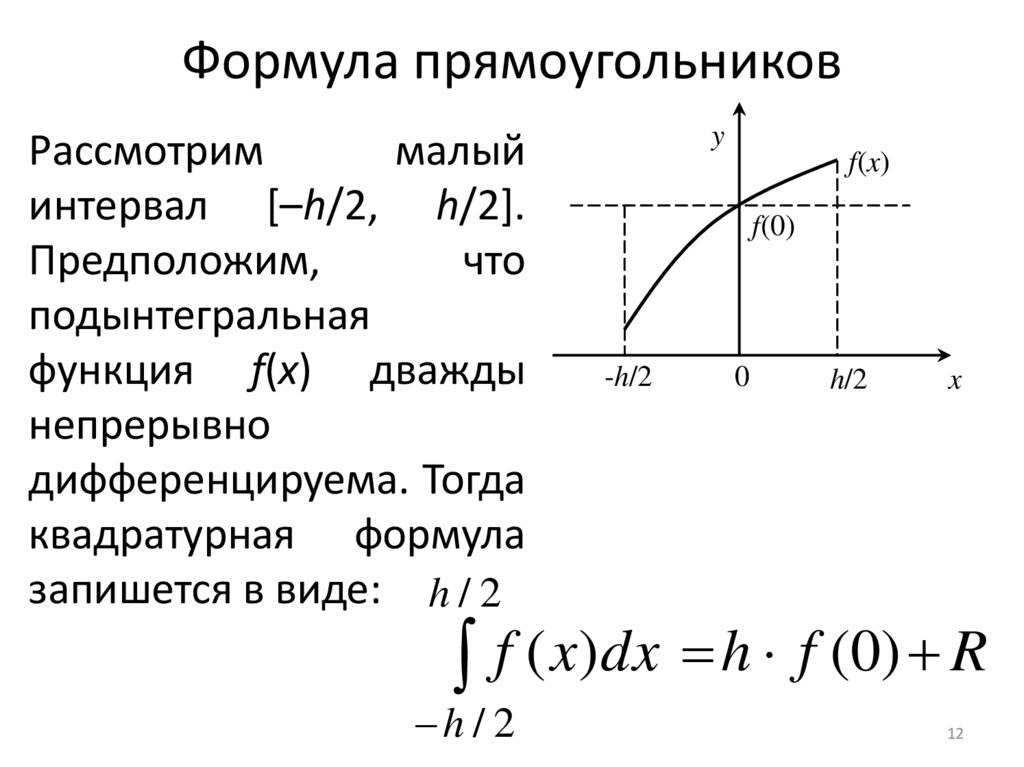
Рассмотрим
малый
интервал [–h/2, h/2].
Предположим,
что
подынтегральная
функция f(x) дважды
непрерывно
дифференцируема. Тогда
квадратурная формула
запишется в виде: h / 2
y
f(x)
f(0)
-h/2
0
h/2
x
f ( x)dx h f (0) R
h / 2
12

13.

Здесь взят один узел = 0 и соответствующий вес
q = h, что соответствует аппроксимации функции
многочленом нулевой степени (константой).
Полученная квадратурная формула называется
формулой прямоугольников для одного шага
или формулой средних:
I = h f(0)
Название определяется тем, что интеграл
функции на участке [–h/2, h/2] заменяется
площадью прямоугольника с высотой f(0) и
основанием h.
13

14.

y
fi+1/2
a
x0 x1 x2
b
xi xi+1
xn-1 xn
x
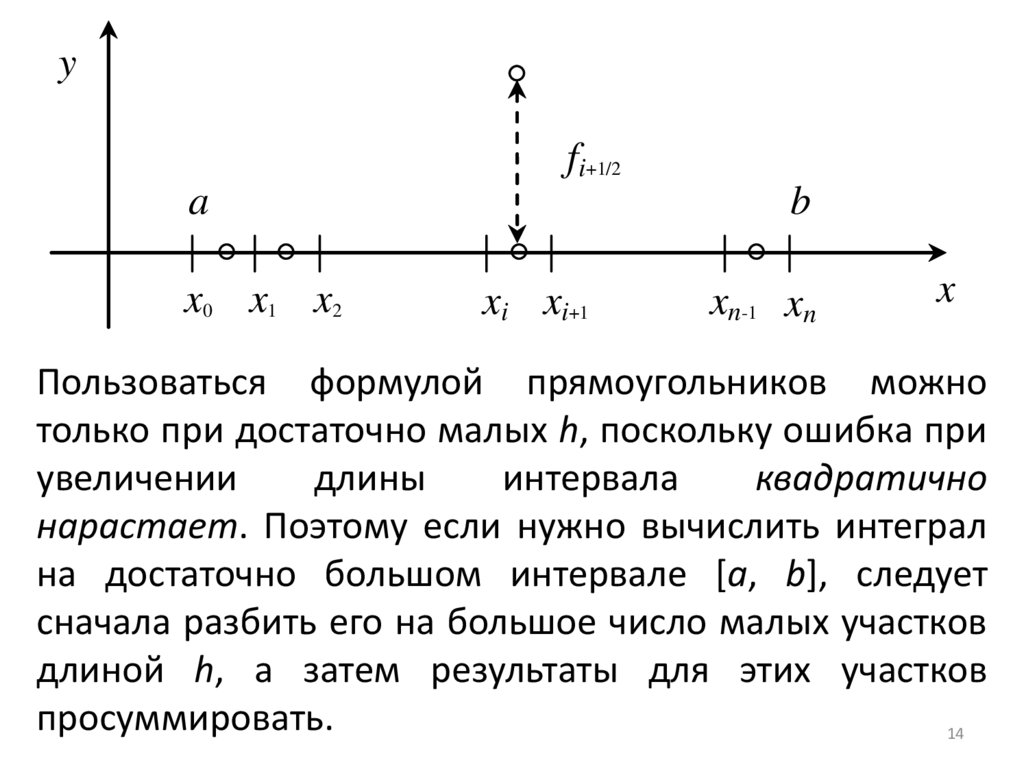
Пользоваться формулой прямоугольников можно
только при достаточно малых h, поскольку ошибка при
увеличении
длины
интервала
квадратично
нарастает. Поэтому если нужно вычислить интеграл
на достаточно большом интервале [a, b], следует
сначала разбить его на большое число малых участков
длиной h, а затем результаты для этих участков
просуммировать.
14

15.

Тогда для i-го интервала будем иметь:
x i 1
3
h
x f ( x)dx hfi 1 / 2 24 f " ( i )
i
где xi i xi+1, 0 i n–1. Суммирование по всем
интервалам приводит к составной формуле
прямоугольников:
b
n 1
f x dx h f
a
i 0
i 1 / 2
R
где погрешность можно оценить как ( [a,b])
h 2 b a
R
f
24
15

16. Формула трапеций

Пусть на малом интервале [0, h] задана дважды
непрерывно дифференцируемая функция f(x)
C2[0,h]. Квадратурное соотношение можно
записать в виде h
f ( 0) f ( h )
f ( x)dx h
0
2
R
где взяты два узла 0 = 0, 1 = h и
соответствующие веса q0 = q1 = h/2, что
соответствует
аппроксимации
функции
многочленом
первой степени
(линейной
функцией).
16

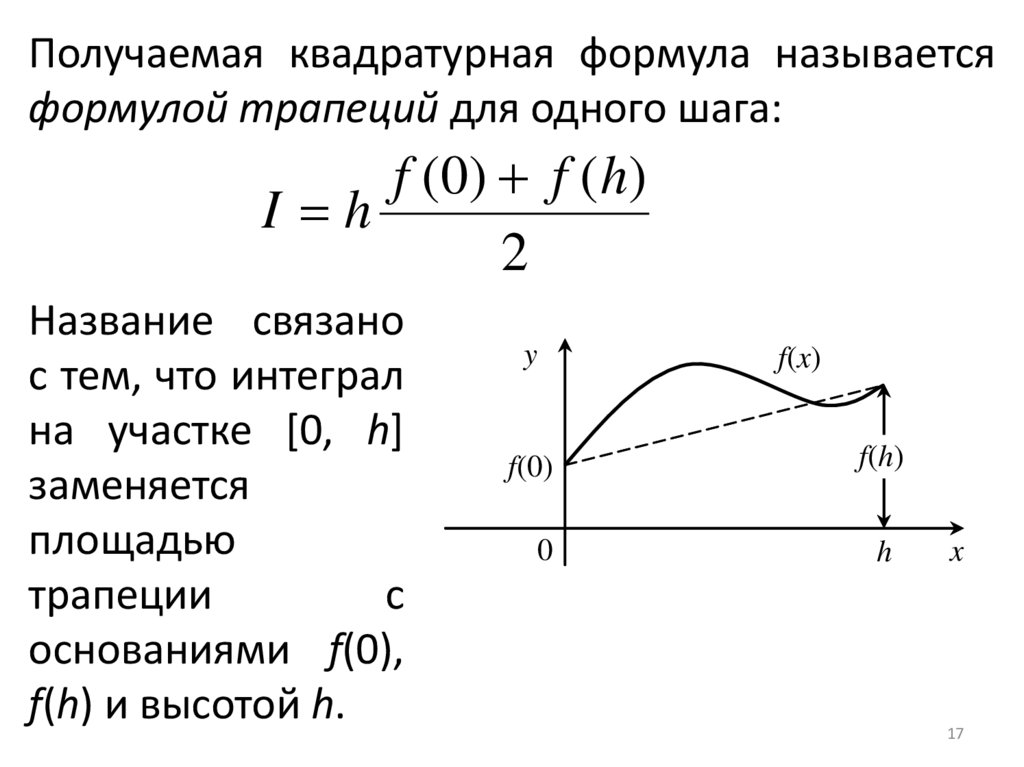
17.

Получаемая квадратурная формула называется
формулой трапеций для одного шага:
f ( 0) f ( h )
I h
2
Название связано
с тем, что интеграл
на участке [0, h]
заменяется
площадью
трапеции
с
основаниями f(0),
f(h) и высотой h.
y
f(x)
f(0)
f(h)
0
h
x
17

18.

y
fi
a
x0
x1 . . .
xi . . .
b
xn
x
Получим формулу трапеций для полного
интервала [a,b], состоящего из большого
числа малых. Обозначим значение функции
f(х) в узлах xi как fi=f(хi).
18

19.

Тогда
по
аналогии
с
формулой
для
прямоугольников
получим
составную
квадратурную формулу трапеций:
fn
f0
f x dx h f1 ... f n 1 R
2
2
a
n 1
h
( f 0 2 fi f n ) R
2
i 1
b
h b a
R
f
12
2
19

20. Формула парабол (Симпсона)

Возьмем малый интервал [–h, h], на котором
определена четырежды дифференцируемая
функция. В квадратурном соотношении возьмем
три узла 0 = xi–1 = –h, 1 = xi =0, 2 = xi+1 =h.
Соответствующие
весовые
коэффициенты
получим из аппроксимации f(x) параболой,
построенной на точках (–h, f(–h)), (0, f(0)), (h,
f(h)) в виде многочлена второй степени:
y = ax2 + bx + c
20

21.

f(x)
y
L(x)
f( h)
h
(xi-1)
f(0)
0
(xi)
f(h)
h
(xi+1)
x
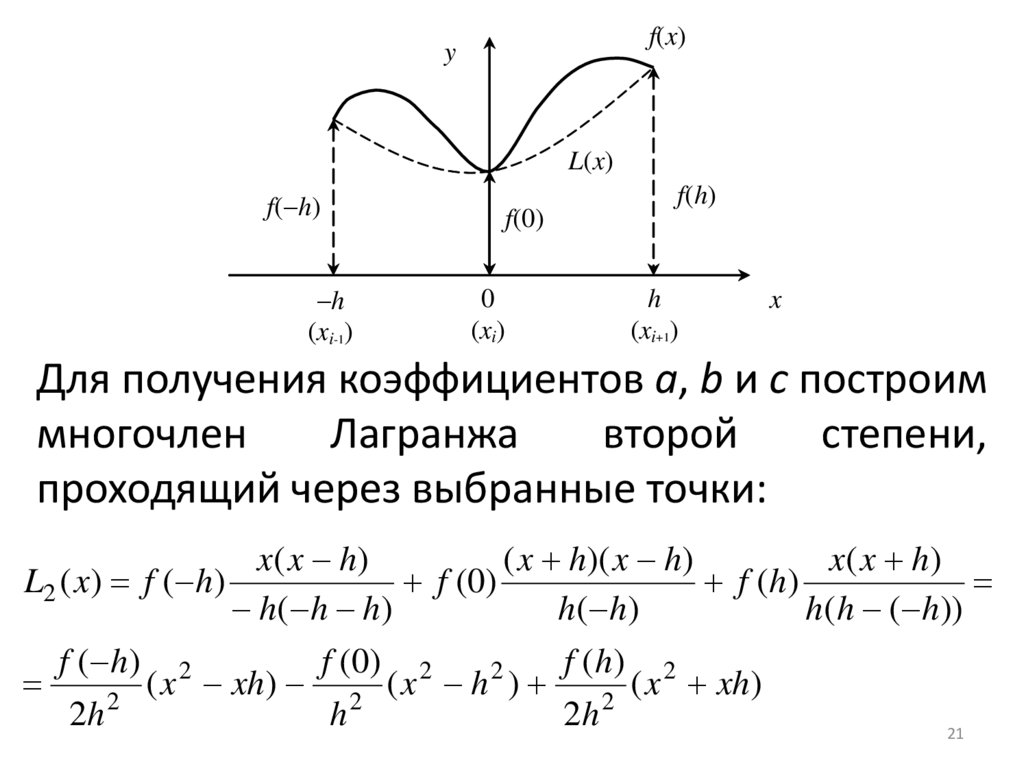
Для получения коэффициентов a, b и c построим
многочлен
Лагранжа
второй
степени,
проходящий через выбранные точки:
x ( x h)
( x h)( x h)
x ( x h)
L2 ( x) f ( h)
f ( 0)
f ( h)
h( h h)
h( h)
h(h ( h))
f ( h) 2
f ( 0) 2
f ( h) 2
2
(
x
xh
)
(
x
h
)
( x xh)
2
2
2
2h
h
2h
21

22.

Вычисляя
интеграл,
получаем
при
соответствующих членах значения весов.
Тогда квадратурная формула для этого
случая примет вид
h
I [ f ( h) 4 f (0) f (h)] R
3
Она называется формулой Симпсона или
формулой парабол.
22

23.

y
i=0
i = m-1
b
a
x0 x1 x2
x2m-2 x2m-1 x2m
x
Для вычисления интеграла на большом
интервале [a, b] разобьем его на четное число
малых интервалов 2m = (b – a)/h.
Для отдельного интервала:
x2 i 2
h
f x dx 3 f 2i 4 f 2i 1 f 2i 2 ,
x2 i
0 i m 1
23

24.

Суммируя по всем интервалам, получим
составную формулу Симпсона:
b
h
f x dx ( f 0 4 f1 2 f 2 4 f3 2 f 4
3
a
... 2 f 2 m 2 4 f 2 m 1 f 2 m )
m
m 1
h
f 0 4 f 2i 1 2 f 2i f 2 m R
3
i 1
i 1
h (b a) IV
R
f ( )
180
4
24

25. Задание

Вычислить интеграл по формуле:
а) прямоугольника,
б) трапеций,
в) Симпсона.

26. Кому какой интеграл?