Численное интегрирование

1.

Численное
интегрирование

2.

Постановка задачи
Необходимо найти значение интеграла
вида
b
I f ( x)dx (1)
a
где a и b – нижний и верхний пределы
интегрирования;
f(x) – непрерывная функция на [a,b].

3.

Способы определения интеграла
b
f ( x)dx S
f ( x) 0
abcd
a
b
n
f ( x)dx lim f ( ) x ; x , x
x 0
a
b
i 1
i
i
i
i
i 1
f ( x)dx F (b) F (a); F ( x) f ( x)
a

4.

В каких случаях применяется
численное интегрирование?
Первообразную невозможно выразить
через элементарные функции.
Аналитическое решение найти
затруднительно.
Функция задана графиком или
таблично.
Функция неизвестна (интегральные
уравнения).

5.

Численное интегрирование
b
b
a
a
f
(
x
)
dx
(
x
)
dx
R
S
R
φ(x) – функция, для которой легко
вычисляется интеграл, например,
многочлен
S – приближённое значение интеграла,
R – погрешность интегрирования.

6.

Квадратурные формулы
Ньютона-Котеса
В общем случае квадратурная формула имеет
вид: b
n
f
(
x
)
dx
f
(
x
)
R
i
i
n
a
i 1
xi – узлы (точки [a, b])
I – веса
Rn – погрешность интегрирования.
(2)

7.

Квадратурные формулы
Ньютона-Котеса
Формулами Ньютона-Котеса называются
квадратурные формулы вида (2) на
равномерной сетке узлов с постоянным
шагом. Различают два типа формул:
замкнутого и открытого типа.
В формулах замкнутого типа x0 = a; xn = b, а в
формулах открытого типа хотя бы один из
этих узлов x0 или xn не совпадает с
соответствующей граничной точкой отрезка.

8.

Квадратурные формулы
Ньютона-Котеса
Разнообразные квадратурные формулы
отличаются выбором xi и i;
способами ускорения сходимости;
способом оценки погрешности R.
друг от друга:

9.

Квадратурные формулы
Ньютона-Котеса
Погрешность зависит как от расположения
узлов, так и от выбора коэффициентов весов. При оценке погрешности в
дальнейшем полагаем, что функция f(x)
достаточно гладкая.
Говорят, что квадратурная формула имеет
алгебраическую степень точности d, если
погрешность равна нулю для любого
полинома степени d, но отлична от нуля для
некоторого полинома степени d+1.

10.

Классификация методов
численного интегрирования
Простейшие формулы, используемые для
приближенного вычисления интегралов,
называют квадратурными, в
многомерном случае - кубатурными.
Сущность большинства методов в
вычислении интегралов состоит в
замене подынтегральной функции f(x)
приближённой функцией φ(x), для
которой легко записать первообразную
в элементарных функциях.

11.

Классификация методов
численного интегрирования
Используемые на практике методы численного
интегрирования можно сгруппировать в
зависимости от способа аппроксимации
подынтегральной функции.
Формулы Ньютона – Котеса используют
полиномиальную замену f(x). Различные методы
этого класса отличаются степенью
используемого полинома.
Для их реализации применяются простые и
универсальные алгоритмы.

12.

Классификация методов
численного интегрирования
Сплайновые методы базируются на
замене f(x) сплайнами. Их имеет смысл
использовать в задачах, где сплайналгоритмы используются для обработки
данных.
Методы наивысшей алгебраической
точности (метод Гаусса - Кристоффеля)
используют неравноотстоящие узлы,
расположенные так, что погрешность
интегрирования минимальна. Эти методы
требуют большого объёма памяти ЭВМ.

13.

Классификация методов
численного интегрирования
Вероятностные методы, в которых узлы
выбираются с помощью датчика случайных
цифр. Эти методы предпочтительны при
нахождении кратных интервалов, хотя они
обеспечивают не очень высокую точность.
Специальные методы учитывают
особенности конкретных подынтегральных
функций, что позволяет сократить время
расчёта и уменьшает погрешность.

14.

Методы прямоугольников
Простейшие методы из класса методов
Ньютона – Котеса, когда подынтегральную
функцию f(x) заменяют полиномом нулевой
степени, т.е.
константой.
Разобьём отрезок [a,b] на n равных частей и
вычислим ступенчатую площадь, равную
сумме площадей прямоугольников с
основаниями h = (b-a)/n и высотами f(xi) или
f(xi+1) или f(xi+h/2).

15.

Метод левых прямоугольников
y
Fn-1
y = f(x)
n 1
F1
F0
0
x0=a
S h f ( xi ) (3)
i 0
h
xn=b
x

16.

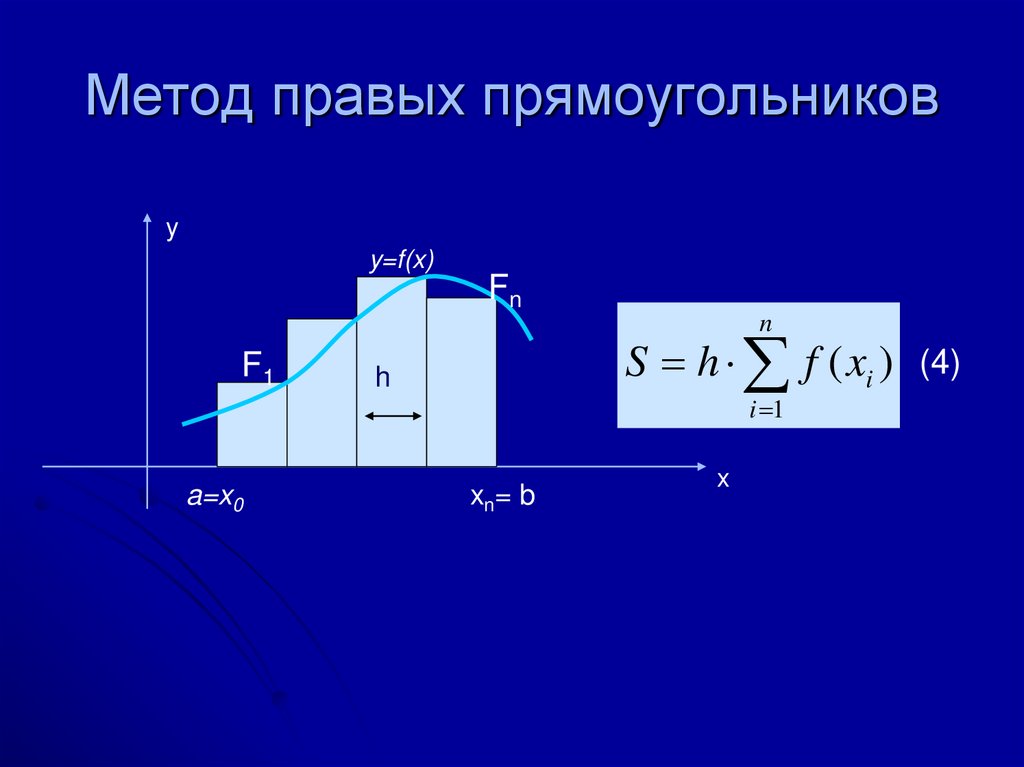
Метод правых прямоугольников
y
y=f(x)
Fn
n
F1
a=x0
S h f ( xi ) (4)
h
i 1
xn= b
x

17.

Метод средних прямоугольников
y=f(x)
n
h
xi
S h f ( xi ) (5)
i 1

18.

Оценка погрешности метода средних
прямоугольников
xi xi 1
Пусть xi 2 , xi 1 xi h.
xi 1
xi 1
xi
xi
Ri f ( x)dx I пр ( f ( x) f ( x i )dx
Разложим f(x) в ряд Тейлора около средней
точки :
( x x)
f ( x) f ( x) f ( x)( x x) f ( x)
xi h
xi h
2
...
( x x) 2
h3
Ri f ( xi ) ( x x)dx f ( xi )
dx ... f ( xi )
2
24
xi
xi

19.

Оценка погрешности метода средних
прямоугольников
Суммируя по промежуткам, получим
x
h2 n
h2 n
R Ri
hf ( xi )
f ( x)dx
24 i 1
24 x0
i 1
n
К последнему интегралу перешли, используя
метод средних прямоугольников.

20.

Оценка погрешности метода средних
прямоугольников
Если функция f(x) на отрезке [a;b] имеет первую
производную, ограниченную значением M, то для
оценки погрешности вычисления интеграла по формуле
средних прямоугольников справедливо соотношение:
M (b a ) 2
R
2n 2
(6)
Полученная теоретическая оценка показывает, что метод
средних прямоугольников имеет второй порядок
точности по h. Аналогично можно доказать, что
методы левых и правых прямоугольников имеют первый
порядок точности.

21.

Метод трапеций
Подынтегральную
y
f(xi+h)
функцию на каждом
отрезке [xi,xi+h] заменим
полиномом первой
f(xi)
степени: прямой. Прямую
проведём через границы
интервала. В этом случае
x
xi
приближённое значение
xi+h
интеграла определяется
площадью трапеции.
xi h
f ( x i ) f ( x i h)
S i f ( x)dx h
2
xi

22.

Метод трапеций
Суммируя по всем промежуткам
1
1
S h f ( x0 ) f ( x1 ) f ( x2 ) ... f ( xn 1 ) f ( xn )
2
2
b a
(7)
y0 2 y1 ... 2 yn 1 yn
2n
В сумму крайние значения входят один раз, а
внутренние дважды. Приведенная формула
называется формулой трапеций.

23.

Оценка погрешности метода
трапеций
Аналогично методу средних прямоугольников находят
оценку погрешности.
Если функция f(x) на отрезке [a;b] имеет вторую
производную, ограниченную значением M, то для
оценки погрешности вычисления интеграла по формуле
трапеций справедливо соотношение:
M (b a )2
R
12n 2
(8)
Таким образом, этот метод имеет также второй порядок
точности, причем R 2 R
тр
пр

24.

Метод Симпсона (парабол)
f(x)
(x)
xi
Подынтегральная функция
заменяется параболой. При
этом комбинируется метод
прямоугольников и трапеций
на [xi,xi+h]:
I=Iпр.+Rпр.
I=Iтр.+Rтр.=Iтр. - 2Rпр.
xi 1
xi
3S 2 Sпр Sтр 2 h f ( x i )
h
h
f
(
x
)
f
(
x
h
)
f ( xi ) 4 f ( x i ) f ( xi 1 )
i
i
2
2
h
Si
f ( xi ) 4 f ( x i ) f ( xi 1 )
6

25.

Удобнее рассматривать промежуток из
двух отрезков, длиной по h каждый:
b a
2h
n
h
I f ( xi ) 4 f ( xi 1 ) f ( xi 2 )
3
Для всего интервала [a,b], разбитого на 2n
частей с шагом
b a
h
2n
применим формулу Симпсона для каждой
пары интервалов.

26.

Формула Симпсона
SСимп
b a
( f (a ) 4 f ( x1 ) f ( x2 )) ( f ( x2 ) 4 f ( x3 ) f ( x4 )) ... f (b)
6n
(9)
b a
f (a ) 4 f ( x1 ) 2 f ( x2 ) 4 f ( x3 ) ... 4 f ( x2 n 1 ) f (b)
6n
Для программирования удобнее пользоваться формулой Симпсона в
следующем виде:
SСимп
2(b a ) f (a ) f (b)
2(
f
(
x
)
f
(
x
)
...
f
(
x
))
f
(
x
)
f
(
x
)
...
f
(
x
)
1
3
2 n 1
2
4
2n
3n
2

27.

Погрешность метода Симпсона
Формула Симпсона может быть получена параболической заменой подынтегральной функции. Поэтому её
называют формулой парабол.
Погрешность данного метода порядка h4:
Mh 4
R
b a , M max f IV ( )
[ a ,b ]
180
(10)
Так как четвёртая производная многочлена 3-ей степени
равна нулю, то формула Симпсона даёт точный
результат для кубической параболы.
Используя рассмотренный подход, можно получить
формулы Симпсона более высокой точности, заменяя
подыинтгральную функцию многочленами степени выше
второй.

28.

Вычисление интеграла
с заданной точностью
Методы Ньютона-Котеса

29.

Как следует из оценочных формул погрешности
методов Ньютона-Котеса, ими можно
воспользоваться лишь тогда, когда f(x) задана
аналитически. Однако даже в этом случае
вместо вычисления производных чаще
применяется следующий универсальный
приём.
Искомый интеграл вычисляется
дважды: [a,b] разбивается на n и на
2n частей.
Полученные Sn и S2n сравниваются и
совпадающие десятичные знаки
считают верными.

30.

Для метода трапеций можно
воспользоваться более точным
неравенством:
Sn S2 n
R
3
(11)
Для метода Симпсона:
Sn S2 n
R
15
(12)

31.

Вычисление интеграла с
заданной точностью
Таким образом, если необходимо вычислить некоторый
интеграл с заданной точностью , необходимо
выполнить следующий алгоритм:
1. Выбрать некоторое число разбиений n отрезка
интегрирования и, соответственно, шаг h.
2. Вычислить значения интеграла Sn и S2n (или Sh и Sh/2).
3. По формулам (11) и (12) вычислить погрешность и
определить ее соответствие заданному условию.
4. Если точность недостаточна, то уменьшить шаг
разбиения вдвое, т.е. до значения h/2, и перейти к п.2.
В противном случае прекратить вычисления.

32.

Метод Монте-Карло
В рассмотренных методах для получения
результата (S) вычисляется сумма yi,
количество слагаемых в которой определяется
числом точек разбиения n отрезка
интегрирования [a,b]. Эти же формулы можно
применить для вычисления кратных
интегралов: для функции многих переменных
по замкнутой многомерной области. При
повышении кратности очень быстро возрастает
число разбиений и объём вычислительной
работы.

33.

Пусть, например, мы разбиваем интеграл
изменения каждой переменной на 10 частей.
Тогда для трехкратного интеграла
необходимо вычислить 1000 слагаемых. Для
десятикратного интеграла потребуется 1010
слагаемых. Это длительная процедура даже
для современных быстродействующих ЭВМ.
В таких случаях предпочтительнее
использовать методы статистических
испытаний (Монте-Карло), которые более
экономичны, хотя обеспечивают не очень
высокую точность.

34.

Существует несколько вариантов метода МонтеКарло для нахождения приближённого
интеграла. Мы рассмотрим два из них. Причём
для простоты изложения рассмотрим случай,
когда кратность равна 1, т.е.
b
I f ( x)dx
a
Идея вычисления интеграла методом Монте-Карло
в простейшем случае (статистическом варианте
метода прямоугольников) состоит в том, что
график интегрируемой функции заменяется
y = f(xi), где xi - случайная точка на отрезке [a,b].

35.

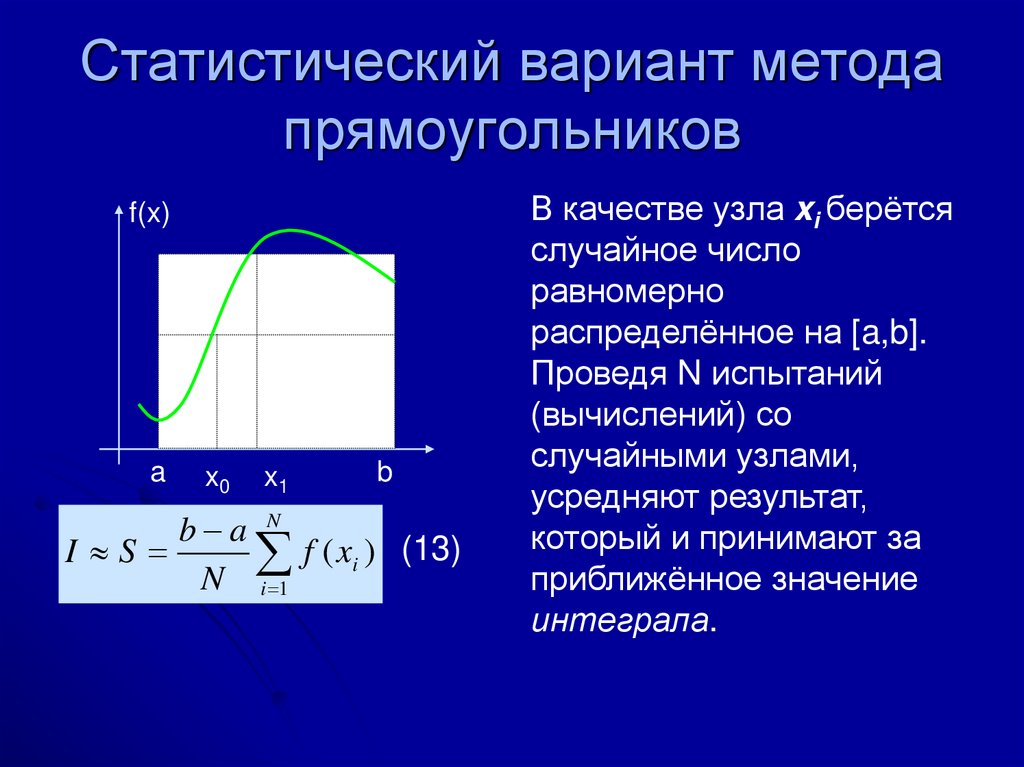
Статистический вариант метода
прямоугольников
f(x)
a
x0
x1
b
b a N
I S
f ( xi ) (13)
N i 1
В качестве узла xi берётся
случайное число
равномерно
распределённое на [a,b].
Проведя N испытаний
(вычислений) со
случайными узлами,
усредняют результат,
который и принимают за
приближённое значение
интеграла.

36.

Погрешность в этом методе не зависит от
кратности интеграла и
пропорциональна 1
N
.
Число узлов, необходимое для
достижения заданной точности,
пропорционально 2 . Это условие
используется для завершения расчёта
и обеспечения заданной точности .

37.

Во втором варианте метода Монте-Карло интеграл
приводится к виду:
1
(u )du
0
где 0 (u) 1 на [0,1]. Это
достигается заменой переменных.
φ(u)
0
1
J
S
N
Тогда две случайных величины xi и (xi)
можно рассматривать как координаты
точек в единичном квадрате. При
равномерном распределении точек в
квадрате за приближённое значение S
интеграла I принимают отношение
количества точек J, попавших под
кривую y = (x), к общему числу
испытаний N.

38.

Метод Монте-Карло
Метод Монте-Карло применим почти для любой
функции и любой области. Он особенно
эффективен при вычислении многомерных
интегралов по областям сложной формы и с
успехом используется при моделировании
различных физических явлений (его первое
применение было связано с исследованием в
рамках Манхэттенского проекта процесса
размножения нейронов).

39.

Метод Гаусса
Для повышения точности интегрирования в
квадратурных формулах отрезок разбивается
на большое количество частей. Достигнуть
заданной точности при малом количестве
узлов позволяет метод Гаусса. Если в
квадратурной формуле узлы интегрирования
выбирают, исходя из условия достижения
наивысшей точности, то вычисления
b
принимают вид: f ( x)dx n A f ( x )
a
i 1
i
i
(*)

40.

Коэффициенты A1, A2,…, An и узлы x1,
x2,…, xn выбираются таким образом,
чтобы интеграл находился по формуле
(*) точно для многочлена как можно
более высокой степени.
Например, с помощью двух узлов (не
считая пределов интегрирования)
можно получить по формуле (*) точный
результат для многочлена 3-й степени.
Для этого сначала с помощью замены
переменной x изменим пределы
интегрирования:
2 x (b a )
b a

41.

1
1
1
I ( )d , где ( )= (b a) f (b a) (b a)
2
2
2
1
1
y
y=α1+α2μ
y=φ(μ)
-1
μ1
μ2
1
μ

42.

Кривая подынтегральной функции заменяется
прямой. В данном случае формула Гаусса
будет иметь вид:
1
1
IG
3
3
Её погрешность определяется формулой:
RG
IV ( )
135
, 1 1.

43.

Сравнение методов
Формула Симпсона при n ординатах даёт
приблизительно ту же степень точности, что и формула
трапеций при 2n ординатах.
Метод Гаусса при n ординатах дает приблизительно ту
же точность, что формула Симпсона при 2n ординатах.
Для достижения той же степени точности по формуле
Симпсона приходится производить приблизительно
вдвое меньше вычислений, чем по формуле трапеций.
Для достижения той же степени точности по методу
Гаусса приходится производить приблизительно вдвое
меньше вычислений, чем по формуле Симпсона.
Формула Симпсона обеспечивает достаточную точность
при умеренном количестве разбиений, проста и удобна,
так как позволяет легко измельчать разбиение и заново
вычислять интеграл. Поэтому она наиболее широко
распространена в практических вычислениях.
Для интегралов высокой степени кратности наиболее
экономичен метод Монте-Карло.