Похожие презентации:
Численное интегрирование
1. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
2. ПОСТАНОВКА ЗАДАЧИ
Если функция f(х) непрерывна наотрезке [a,b] и известна ее
первообразная F(x), то
определенный интеграл от этой
функции в пределах от a до b
может быть вычислен по формуле
Ньютона-Лейбница
b
f ( x)dx F (b) F (a),
a
где F ( x) f ( x)
'
3. Но часто возникают ситуации, когда вычислить интеграл можно только с помощью численных методов:
1) F(x) не выражаетсячерез элементарные функции.
b
e
x2
dx
a
2) F(x) существует и выражается через элементарные
функции, но ее сложно найти
x x ... 1
a x 40 x39 ... 1dx
b
30
29
3) Найдена F(x), но сложно вычислить ее значение;
4) f(х) задана таблично или графиком.
4. Итак, как вычислить
bИтак, как вычислить f ( x)dx
a
Обычный прием состоит в том, что данную функцию
f(х) на рассматриваемом отрезке [a,b] заменяют
интерполирующей функцией Pn(x) простого вида, а
b
затем приближенно полагают: b
f ( x)dx ( x)dx
n
a
a
Функция Pn(x) должна быть такова, чтобы интеграл
вычислялся непосредственно.
Можно использовать интерполяционный
многочлен Pn(x) различной степени n, n = 0, 1, 2, ...
5. Формулы прямоугольников
При n=0 , f ( x ) 0 ( x )Для построения Р0(х) требуется
одна точка (х0, f(х0) ).
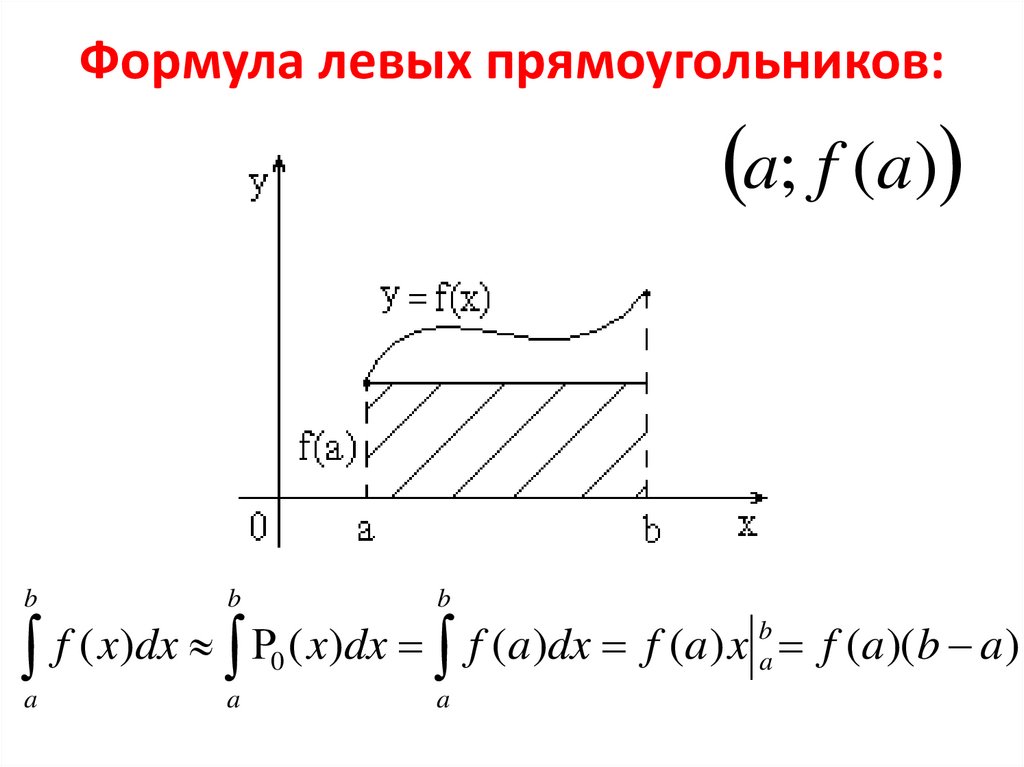
6. Формула левых прямоугольников:
a; f (a)b
a
b
b
a
a
f ( x )dx 0 ( x )dx f (a )dx f (a ) x ba f (a )( b a )
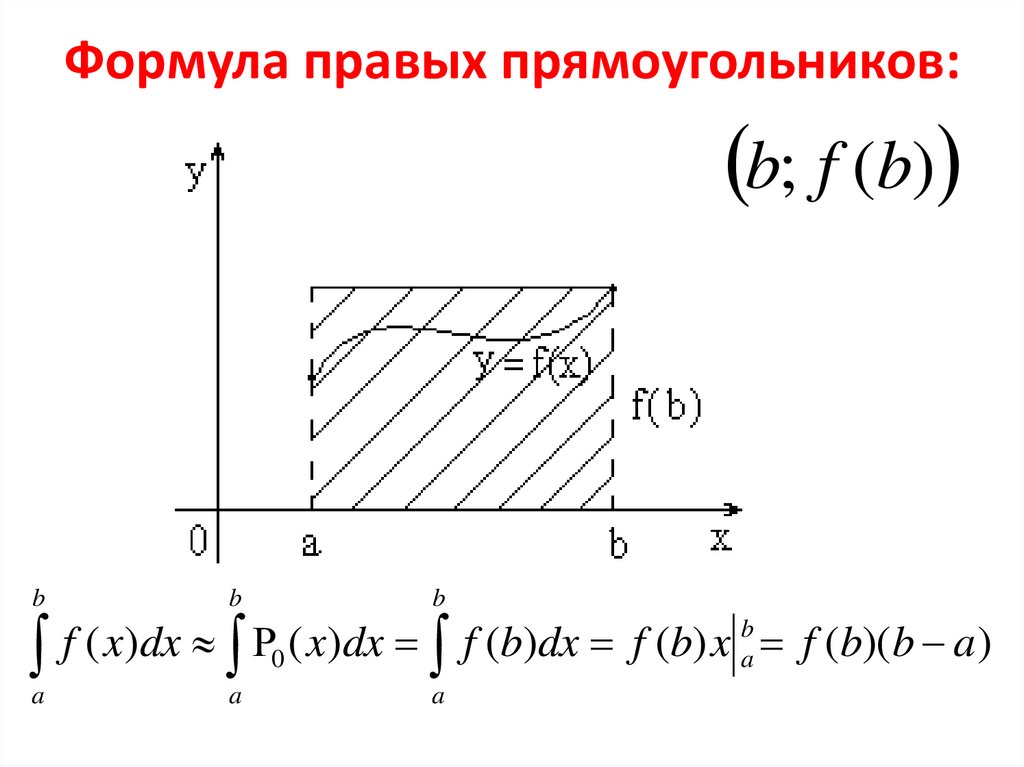
7. Формула правых прямоугольников:
b; f (b)b
b
b
f ( x)dx ( x)dx f (b)dx f (b) x
0
a
a
a
b
a
f (b)( b a )
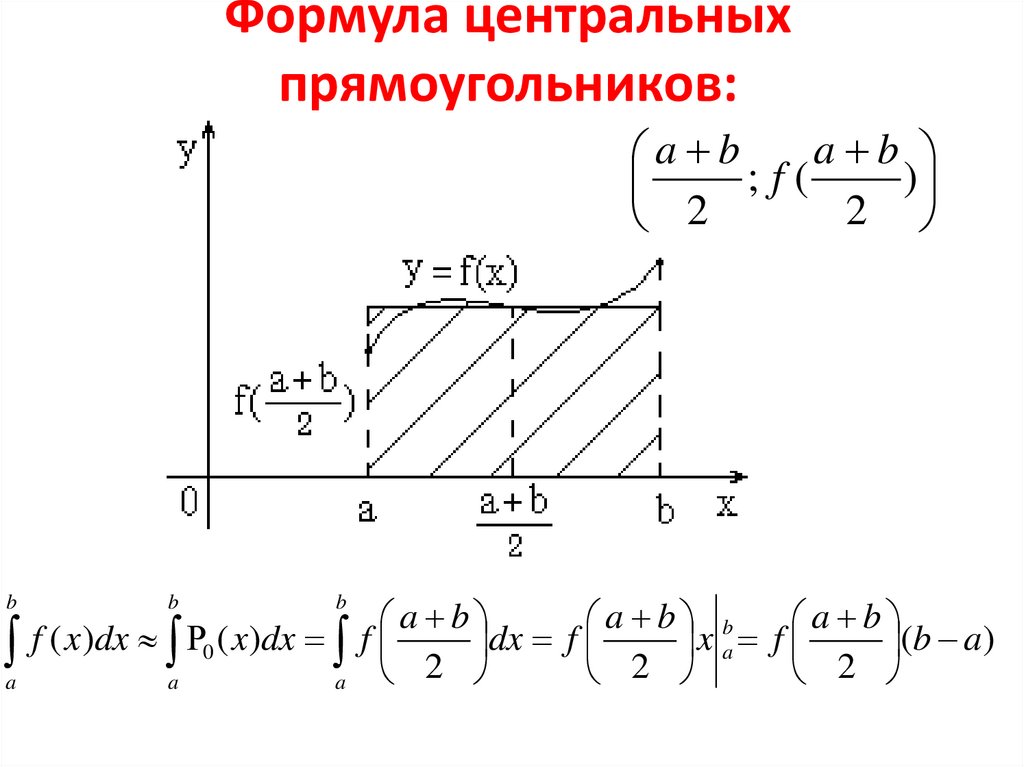
8. Формула центральных прямоугольников:
a ba b
;f(
)
2
2
b
b
b
f ( x)dx ( x)dx
0
a
a
a
a b
a b b
a b
f
dx f
x a f
(b a )
2
2
2
9. Обобщенные формулы
На практике обычно пользуются обобщеннымиформулами, т.к. [a,b] может быть большим и,
следовательно, большой и погрешность
вычисления интеграла по формулам
прямоугольников, трапеции и Симпсона.
Для повышения точности вычисления [a,b]
разбивают на n равных частей точками
a=x0<x1< ... < xn=b, и на каждом отрезке [xi, xi+1]
применяется конкретный метод прямоугольников,
трапеции или Симпсона, результаты суммируются.
Величина h=(b-a)/n - шаг интегрирования,
xi=x0+ih, где i=0,…,n.
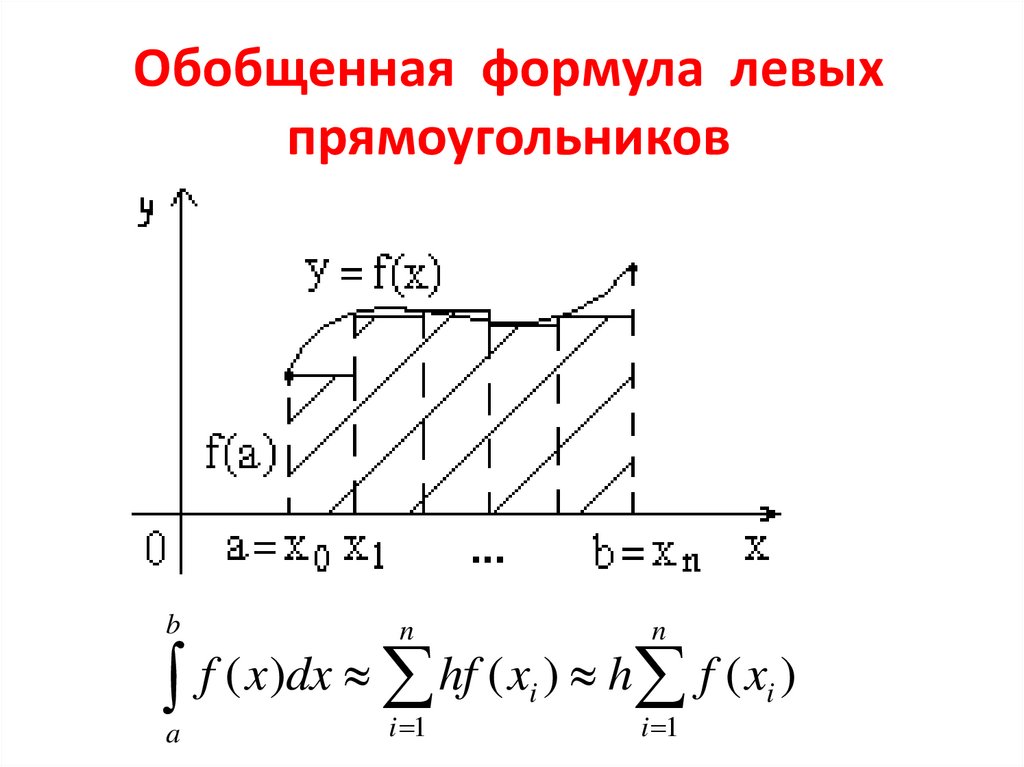
10. Обобщенная формула левых прямоугольников
bn
n
f ( x)dx hf ( x ) h f ( x )
a
i 1
i
i 1
i
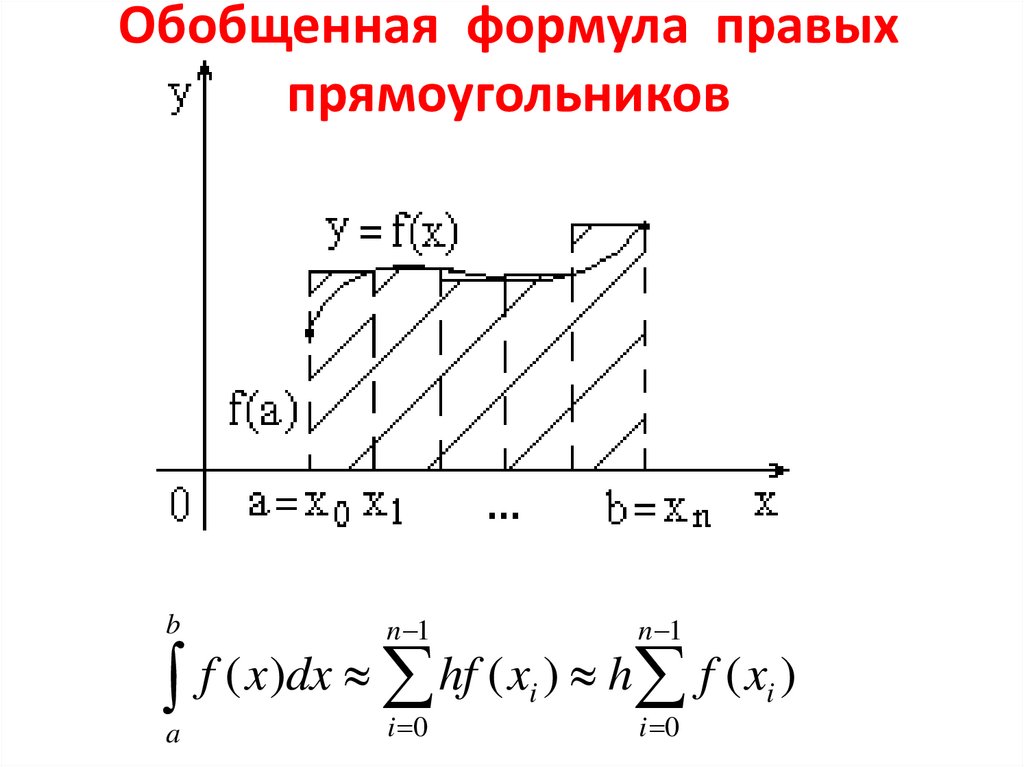
11. Обобщенная формула правых прямоугольников
bn 1
n 1
f ( x)dx hf ( x ) h f ( x )
a
i 0
i
i 0
i
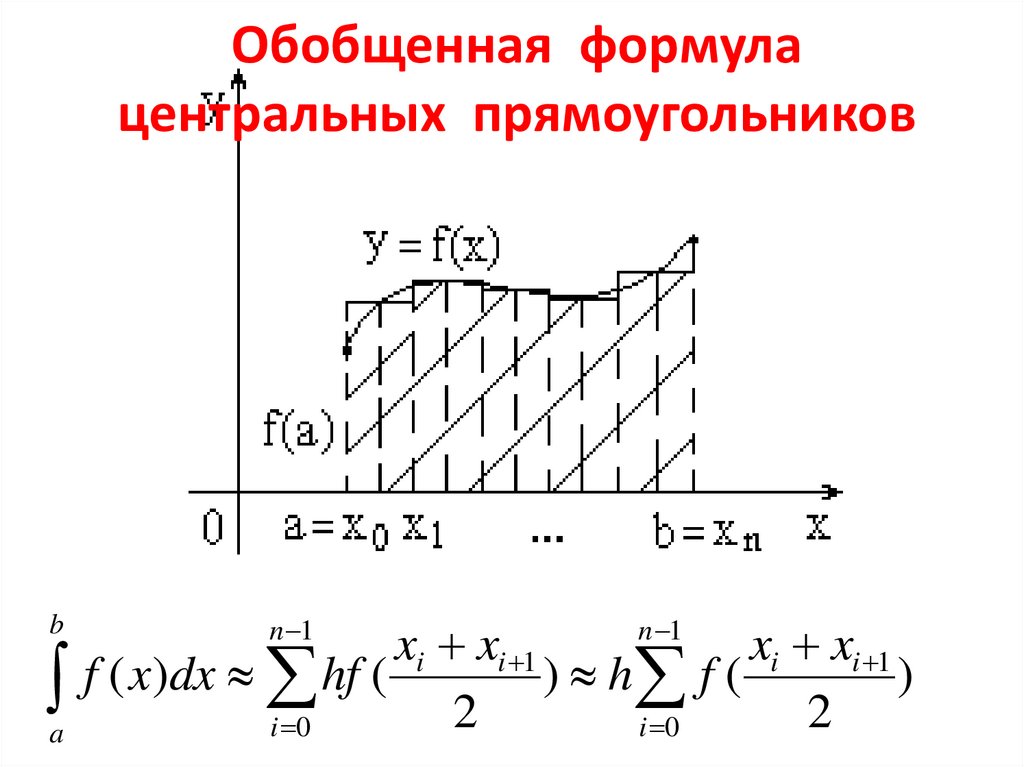
12. Обобщенная формула центральных прямоугольников
ba
n 1
xi xi 1
xi xi 1
f ( x)dx hf (
) h f (
)
2
2
i 0
i 0
n 1
13. Эмпирический критерий оценки точности вычисления интеграла
На практике широко применяетсяследующий прием, пригодный для
каждого из рассматриваемых методов.
Искомый интеграл вычисляется дважды:
при делении отрезка [a,b] на n частей и
на 2n частей. Полученные интегралы Jn
J2n сравниваются, и совпадающие
первые десятичные знаки считаются
верными.
14. Вычислить интеграл по формулам левых и правых прямоугольников при n=10, оценивая точность с помощью сравнения полученных
результатов.12
6 х 3dx
2
2
При n=10 разобьем отрезок
интегрирования на 10 частей с шагом
b a 12 2
h
1
n
10
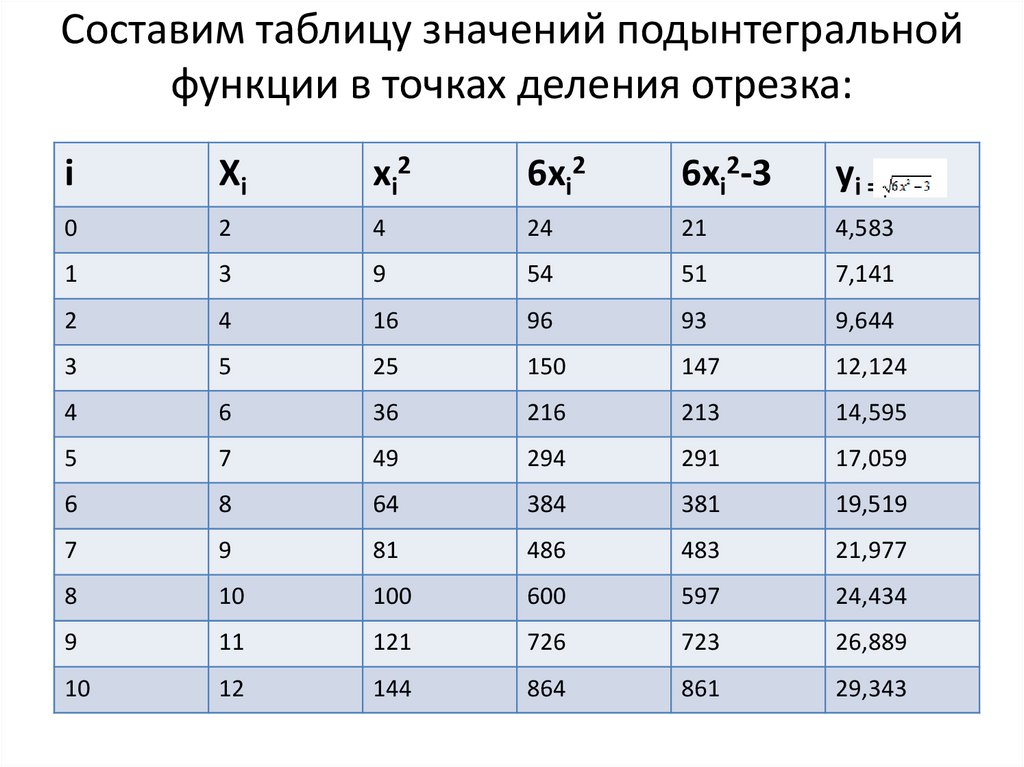
15. Составим таблицу значений подынтегральной функции в точках деления отрезка:
iXi
xi2
6xi2
6xi2-3
yi =
0
2
4
24
21
4,583
1
3
9
54
51
7,141
2
4
16
96
93
9,644
3
5
25
150
147
12,124
4
6
36
216
213
14,595
5
7
49
294
291
17,059
6
8
64
384
381
19,519
7
9
81
486
483
21,977
8
10
100
600
597
24,434
9
11
121
726
723
26,889
10
12
144
864
861
29,343









 Математика
Математика