Похожие презентации:
Численное интегрирование
1. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
2.
Если функция f(x)непрерывна на отрезке a,b
то определенный интеграл
от этой функции
в пределах от a до b
существует и имеет вид
b
f ( x )dx F ( b ) F ( a )
a
3. Задача численного интегрирования
Найти определенный интегрална отрезке a,b
если подынтегральная функция
на отрезке задана таблично.
Формулы
приближенного интегрирования
называются
квадратурными формулами.
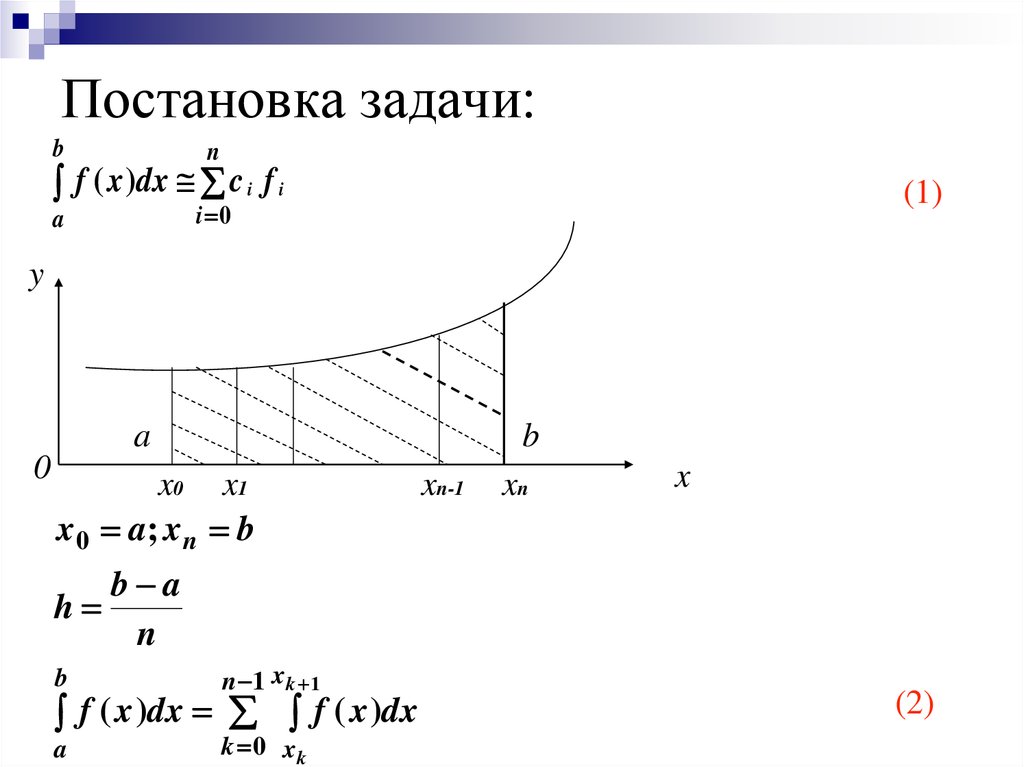
4. Постановка задачи:
bn
f ( x )dx c i f i
(1)
i 0
a
y
a
0
b
x0 x1
x 0 a; x n b
xn-1
xn
x
b a
h
n
b
n 1 x k 1
a
k 0 xk
f ( x )dx f ( x )dx
(2)
5. Погрешность численного интегрирования
x k 1k - погрешность вычисления интеграла f ( x )dx
xk
- погрешность в малом
En
- погрешность вычисления интеграла
b
n 1 x k 1
a
k 0 xk
f ( x )dx f ( x )dx - погрешность в целом
6. Связь
Пустьk
и En
k o( h )
p
b a
E n k n max k
max k
k
k
h
E n o( h
p 1
)
7. Метод прямоугольников
основан на непосредственномопределении интеграла:
b
n 1
a
i 0
f ( i ) xi
f ( x )dx nlim
n 1
где
f ( i ) xi - интегральная сумма, соответствующая
i 0
некоторому разбиению отрезка a,b
и некоторому выбору точек
0 , 1 ,…, n 1
на отрезках разбиения
8.
Вычисление определенногоинтеграла
b
I f ( x )dx
a
геометрически сводится
к вычислению площади
криволинейной трапеции,
ограниченной функцией f(x),
осью абсцисс и прямыми x = a и x = b.
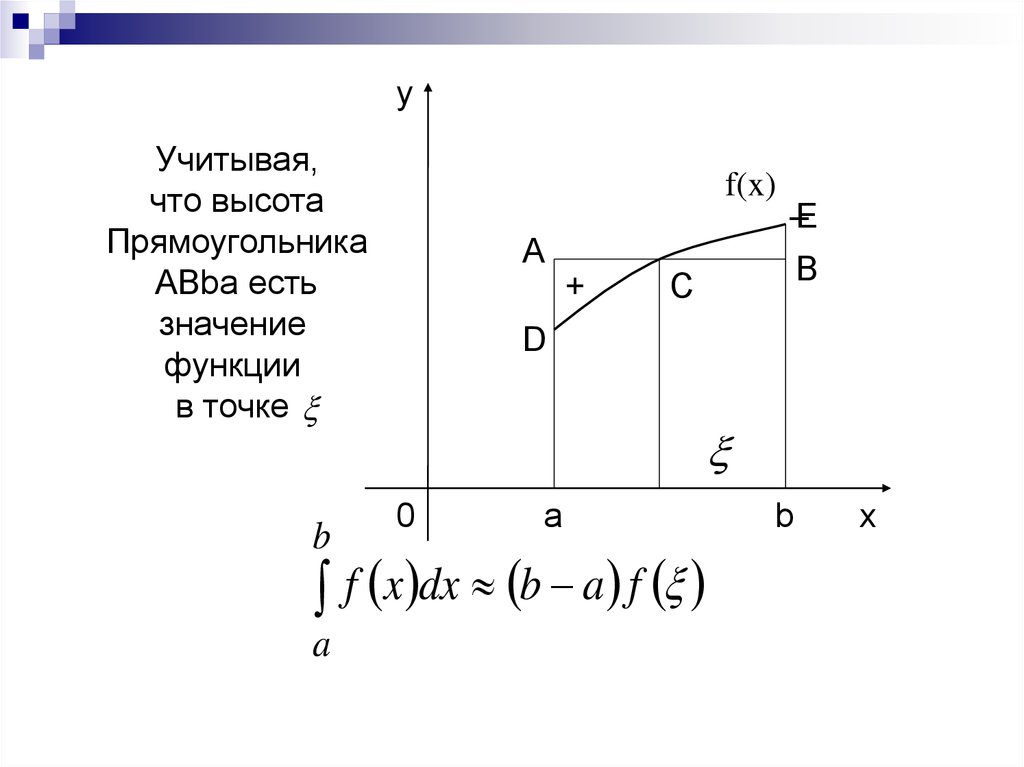
9.
yУчитывая,
что высота
Прямоугольника
ABba есть
значение
функции
в точке
b
f(x)
A
+
B
C
D
0
a
f x dx b a f
a
–E
b
x
10.
Для увеличения точностичисленного интегрирования
можно отрезок a,b
разбить на несколько частей
и для каждой из них вычислить
приближенное значение
площади криволинейной
трапеции, основанием которой
является отрезок
xi xi 1 xi (i = 0, 1, …,n – 1),
а высотой число
f i т.е. значение функции
в точке i xi , xi 1
b
f x dx f 0 x0 f 1 x1 f 2 x2 f n 1 xn 1
a
11.
Практически удобно делитьотрезок a,b
на равные части, а точки
i (i = 0, 1, …, n – 1) совмещать с левыми
f i f xi
или с правыми f i f xi 1
концами отрезков разбиения.
12.
Если точку iсовместить с левым концом
отрезка xi
то приближенное значение
интеграла может быть
представлено
формулой левых
прямоугольников:
n 1
b a
I л f x dx
y0 y1 y n 1 h y i
n
i 0
a
b
где
b a
h
n
– шаг.
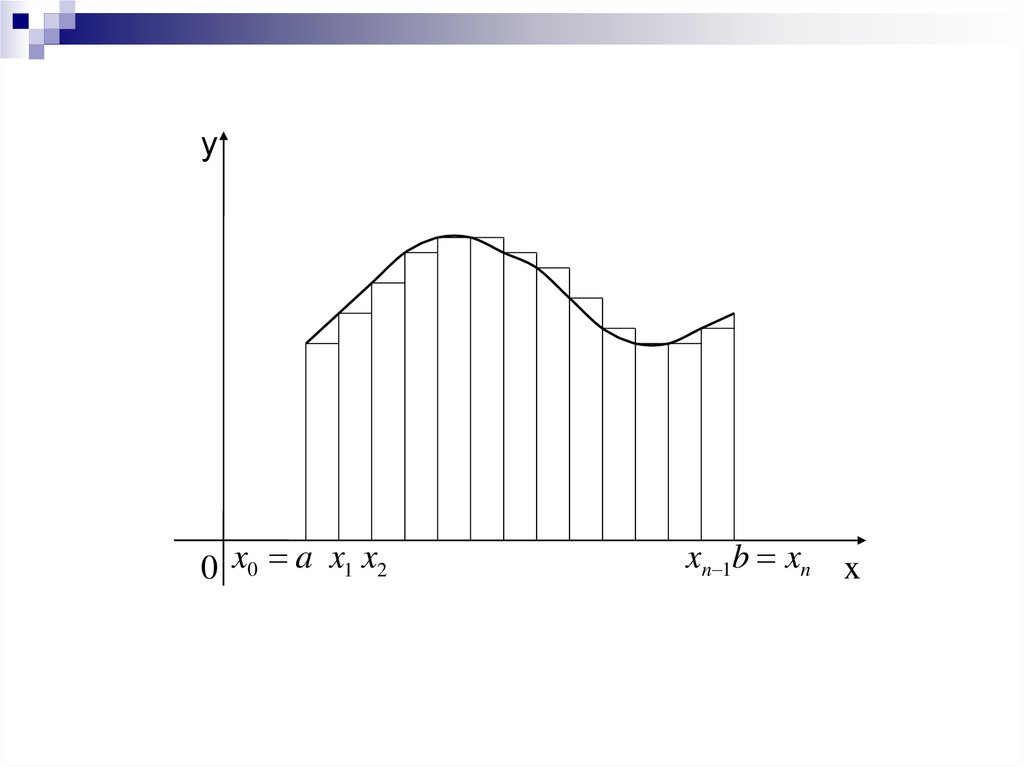
13.
y0 x0 a x1 x2
xn 1b xn x
14.
.Если же в качестве точки i
выбрать правый конец отрезка xi
то приближенное значение
интеграла вычисляется
по формуле правых
прямоугольников:
n
b a
I П f x dx
y1 y2 yn h yi
n
i 1
a
b
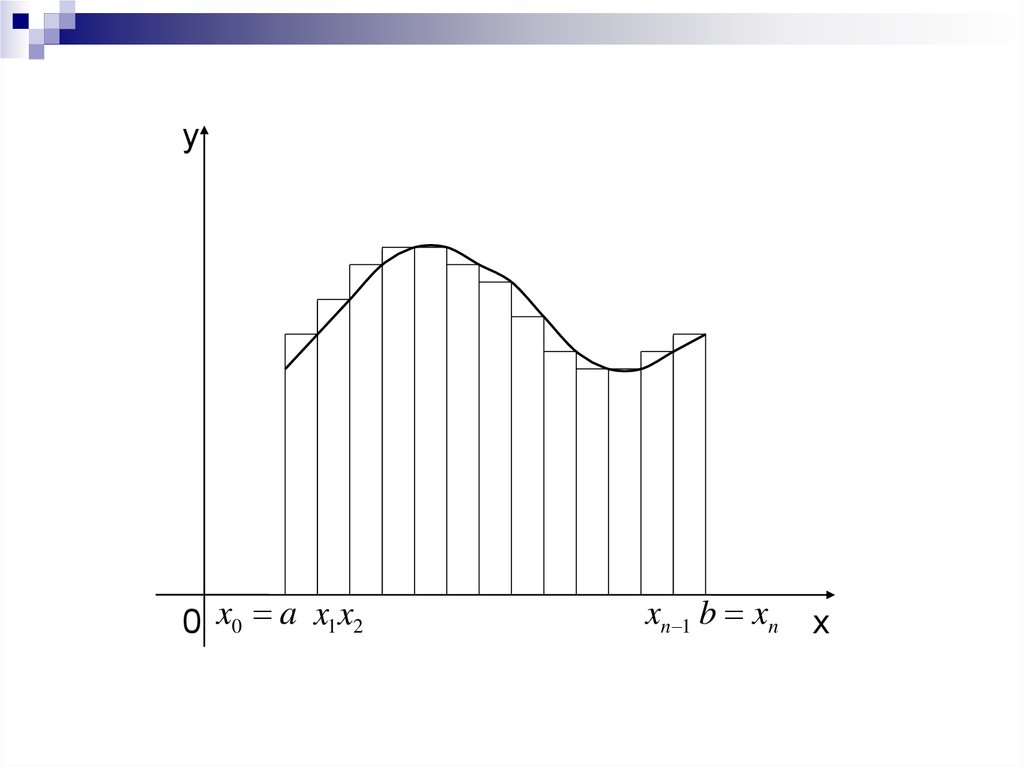
15.
y0 x0 a x1x2
xn 1 b xn
x
16.
Формула средних прямоугольниковy
xk 1
f ( x )dx f
xk
f
f(x)
1
k
2
f (x
1
k
2
1
k
2
)
b
n 1
a
k 0
f ( x )dx h f
a
b
x0
xn
h
k
1
2
– составная формула
x
17. Погрешность формул средних прямоугольников
kxk 1
f ( x)dx f
xk
k
xk 1
xk
k
1
2
h
xk 1
f ( x) f 1 dx f 1 x x k 1
k 2
k
2
2
xk
h
2
h
2
x x k 1
2
f 1
2
k 2
z2
h3
4
f 1 zdz f 1 dz o(h )
f 1 o(h 4 )
k
k
24 k 2
2
2
h
h 2
2
2
b a h3
(b a )h 2
E
M2
M2
h 24
24
об
M 2 max f 1
k 0 , n 1
k
2
2
o x x
1
k
2
3
dx
18. Метод трапеций
Заменим на отрезке a,bдугу AB графика
подынтегральной функции y = f(x)
стягивающей ее хордой и
вычислим площадь трапеции ABba.
Примем значение определенного
интеграла численно равным
площади этой трапеции:
f a f b
f x dx b a
2
a
Это и есть формула трапеций
b
19.
yf(x)
B
A
0
a
b
x
20.
Если отрезок a,bразделить на несколько
частей и применить
формулу трапеции
к каждому отрезку xi
Тогда
f xi f xi 1
xi
f x dx
2
xi
x i 1
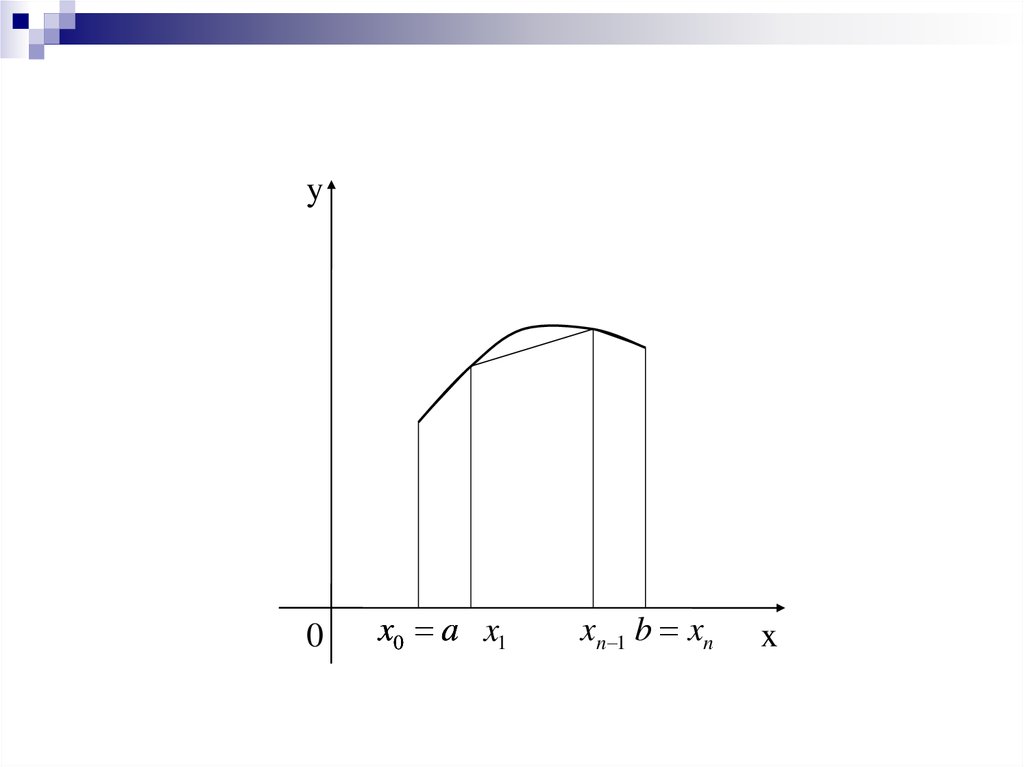
21.
y0
x0 a x1
xn 1 b xn
x
22.
Для простоты вычисленийудобно разделить отрезок a,b
на равные части,
в этом случае длина
каждого из отрезков
разбиения есть
b a
x i
n
Численное значение
интеграла на отрезке xi
равно
b a f xi f xi 1
f x dx n
2
xi
x i 1
23.
А на всем отрезкеa,b
соответственно
b a n 1 f xi f xi 1 b a n 1 yi yi 1
f x dx n
2
n i 0
2
i 0
a
b
Эта формула называется
общей формулой трапеции.
Ее можно переписать в виде
b
h
f x dx 2 y0 2 y1 2 y 2 2 y n 1 y n
a
b a
h
где
– шаг.
n
24. Погрешность формулы трапеций
kxk 1
xk 1
r ( x)dx
1
xk
M2
2
xk
xk 1
M2
x xk x xk 1 dx
2
M 2 h3
x x xk x xk 1 dx 12
k
M2 2
E
h (b a )
12
об
M 2 max f 1
k 0 , n 1
k
2
25. Составная формула трапеции
bh
f ( x )dx ( f 0 f1 f1 f 2 f 2 f 3 ...
2
a
n 1
h
f n 1 f n 1 f n ) f 0 f n 2 f k
2
k 1
об
M 2,k 3
k
h , где M 2 max f 1
k 0 , n 1 k
12
2
M2
2
En
(b a )h
12
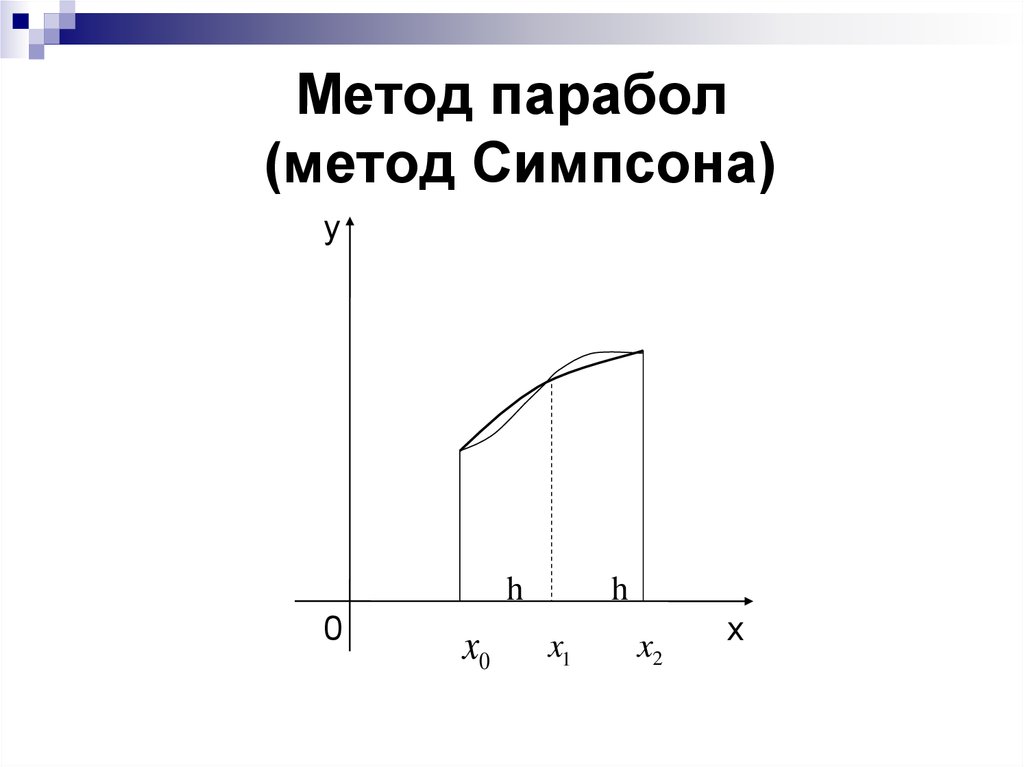
26. Метод парабол (метод Симпсона)
yh
0
x0
h
x1
x2
x
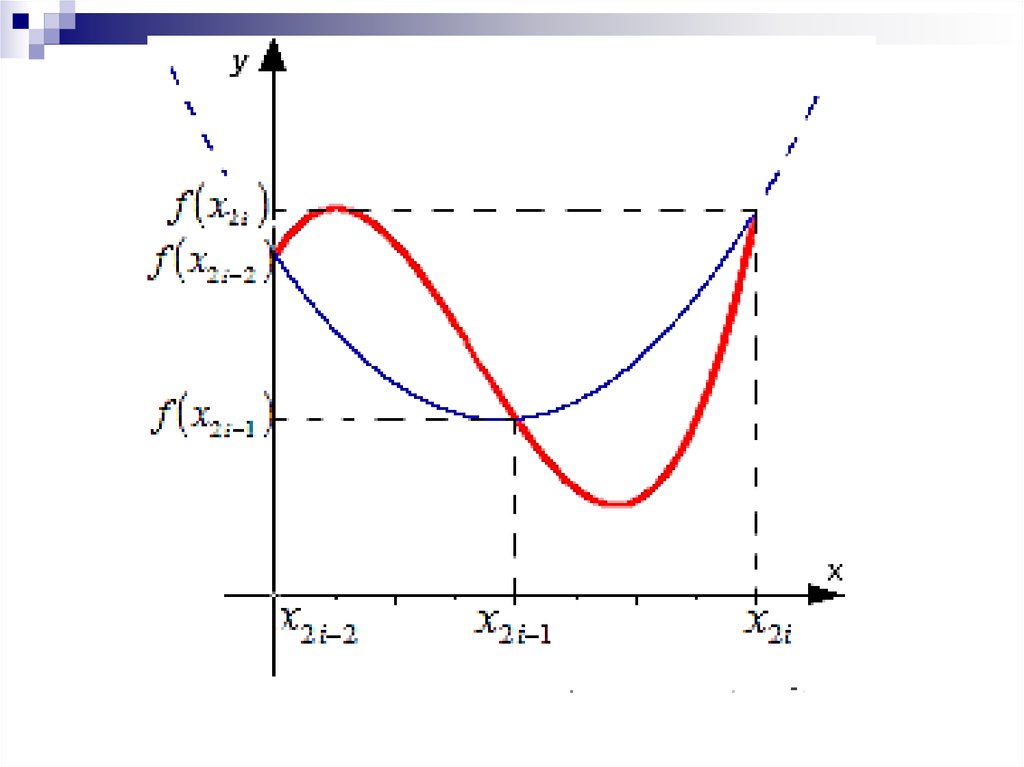
27. Графическая иллюстрация метода парабол (Симпсона)
28. Формула Симпсона
29.
30.
Определитель матрицы отличен от 0 =>система уравнений имеет единственное
решение
31. Через данные точки проходит единственная квадратичная парабола
32. Вычислим значение функции в точках
33. Найдём интеграл
34.
Для увеличения точностивычислений отрезок a,b
разбивают на n пар участков
x2i 2 , x2i 1 , x2i
и заменяя подынтегральную
функцию интерполяционным
многочленом Ньютона
второй степени, получают
приближенное значение
интеграла на каждом участке
длины 2h:
35.
x2f x dx
x0
x4
x2
h
y0 4 y1 y2
3
f x dx
h
y 2 4 y3 y 4
3
……………………………………
x2 n
h
f x dx y2 n 2 4 y2 n 1 y2 n
3
x2 n 2
36.
Тогда численное значениеопределенного интеграла
на отрезке a,b
будет равно сумме интегралов
b
f x dx
a
h
y0 y 2 n 4 y1 . y 2 n 1 2 y 2 y 2 n 2
3
Это соотношение называется
общей формулой Симпсона.
Ее можно записать также в виде
b
a
f x dx
b a
y0 y 2 n 4 y1 . y 2 n 1 2 y 2 y 2 n 2
6n
где h b a
2n
37. Составная формула Симпсона
bh
f ( x )dx ( f 0 4 f1 f 2 f 2 4 f 3 f 4 ...
3
a
n
n 1
2
2
h
f n 2 4 f n 1 f n )
f 0 f n 4 f 2 k 1 2 f 2 k
3
k 0
k 1
M4 5
k
h
90
M4
4
En
( b a )h
90
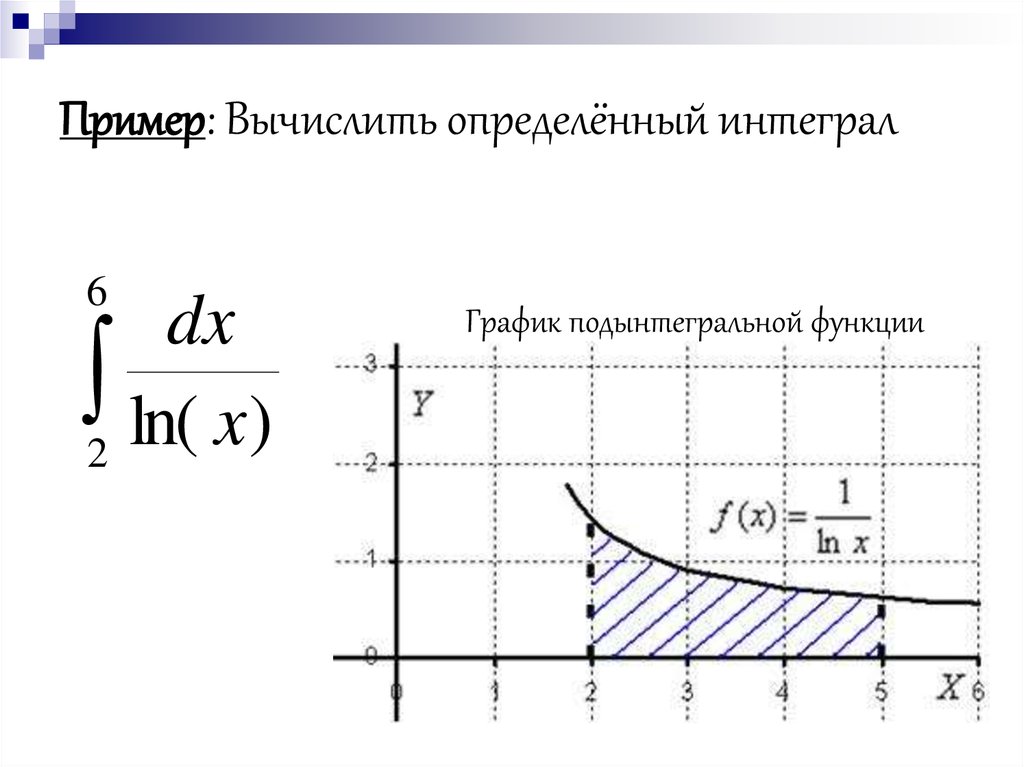
38. Пример: Вычислить определённый интеграл
6dx
2 ln( x)
График подынтегральной функции
39. Ответ:
40. Метод Монте-Карло
Методы Монте-Карло – это общееназвание группы методов для решения
различных задач с помощью случайных
последовательностей. Название этой
группе методов дал город Монте-Карло
– столица европейского игорного
бизнеса (казино).
41.
Сущность метода Монте-Карлосостоит в следующем:
Требуется найти значение а некоторой
изучаемой величины.
Для этого выбирают такую случайную
величину X, математическое ожидание
которой равно а:
М(Х)=A.
42. Пример использования метода Монте-Карло
Предположим, что нам нужно определить площадь плоскойфигуры, расположенной внутри квадрата, сторона которого
равна единице , при этом площадь квадрата Sкв=1. Выберем
внутри квадрата наугад N точек. Обозначим через M количество
точек, попавших при этом внутрь фигуры. Тогда площадь
фигуры S приближенно равна отношению M/N . Отсюда, чем
больше N, тем больше точность такой оценки.
S/Sкв≈M/N или
S ≈ M/N
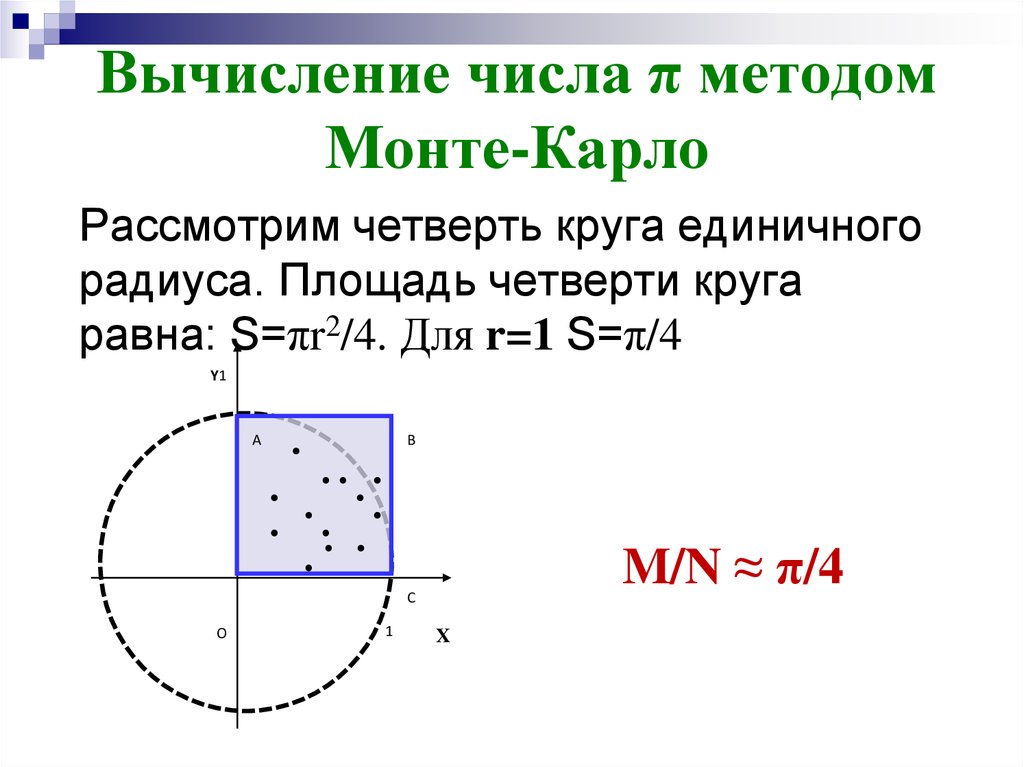
43. Вычисление числа π методом Монте-Карло
Рассмотрим четверть круга единичногорадиуса. Площадь четверти круга
равна: S=πr2/4. Для r=1 S=π/4
Y1
A
B
M/N ≈ π/4
C
O
1
X




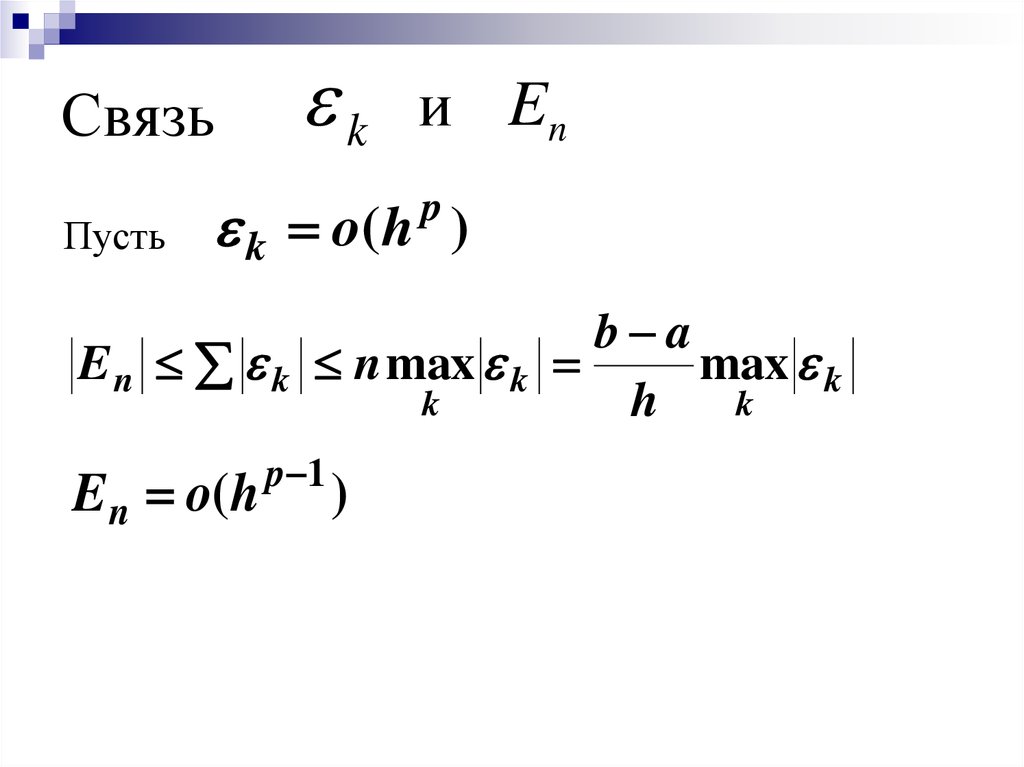





























 Математика
Математика