Похожие презентации:
§8. Теория систем линейных алгебраических уравнений
1.
§8. Теория систем линейныхалгебраических уравнений
п.1. Базисные и свободные переменные
Рассмотрим систему линейных уравнений
a11 x1 a12 x 2 a1n x n b1 ,
a x a x a x b ,
21 1 22 2
2n n
2
a m1 x1 a m 2 x 2 a mn x n bm .
2.
r( A) r( A)Совместная система линейных уравнений
называется определенной, если на имеет одно
решение.
Совместная система линейных уравнений
называется неопределенной, если на имеет
бесконечное количество решений.
r(A) n
r(A) r
3.
Неравный нулю минор r-го порядка матрицыранга r называется базисным.
Если коэффициенты при r переменных
совместной системы образуют базисный
минор матрицы системы, то эти r переменных
называют базисными (основными).
Остальные n r переменные называются
свободными (неосновными).
Базисные переменные можно выбрать
различными способами.
Решение, в котором все свободные
переменные равны нулю, называется
базисным.
4.
Пример.2 x1 x2 x3 x4 5,
x1 2 x2 2 x3 3 x4 6,
3 x x x 2 x 1.
4
1 2 3
Решение.
3 6
1 2 2 3 6 1 2 2
2
1
1
1
5
~
0
5
5
7
17
~
3 1 1 2 1 0 5 5 7 17
3 6
1 2 2
~
5 7 17
0 5
r 2
5.
x1 2 x 2 2 x3 3 x 4 6,5 x 2 5 x3 7 x 4 17;
x1 , x 2 ꟷ базисные
x 3 , x 4 ꟷ свободные
x1 2 x 2 6 2 x3 3 x 4 ,
5 x 2 17 5 x3 7 x 4 ;
17
7
x 2 x3 x 4
5
5
7
4 1
17
x1 6 2 x 3 x 4 2 x 3 3 x 4 x 4
5
5 5
5
4 1
17
7
x1 c 2 , x 2 c1 c 2 , x 3 c1 , x 4 c 2
5 5
5
5
6.
п.2. Однородные системы линейныхуравнений
Система вида
a11 x1 a12 x2 a1n x n 0,
a x a x a x 0,
21 1 22 2
2n n
a m1 x1 a m 2 x 2 a mn x n 0,
называется однородной системой линейных
уравнений.
7.
Замечание.Однородная система линейных уравнений
всегда совместна.
Решение однородной системы
x1 x 2 ... x n 0
называется тривиальным.
8.
Теорема 1.Для того, чтобы однородная система
линейных уравнений имела нетривиальное
решение, необходимо и достаточно, чтобы
ранг матрицы коэффициентов был меньше
количества неизвестных, т.е.
r( A ) n.
Доказательство.
Необходимость. От противного.
Пусть система имеет нетривиальное решение,
но
r( A ) n.
9.
Выпишем систему, состоящую из nсоответствующих уравнений.
Она имеет единственное решение, которое
находится по правилу Крамера.
При этом все
значит
i 0,
x1 x 2 ... x n 0 .
Получили противоречие с условием, поэтому
r( A ) n.
10.
Достаточность.Пусть
r( A ) n.
Так как система совместна, то она имеет
бесконечное количество решений (хотя бы
одно ненулевое).
11.
Следствие.Если число уравнений однородной системы
равно числу неизвестных, то она имеет
ненулевое решение тогда и только тогда, когда
определитель матрицы коэффициентов равен
нулю.
12.
Пример.2 x1 3 x 2 x3 0,
x1 2 x 2 x3 0,
x
2 x3 0 .
1
Решение.
2
3 1
det A 1 2
1 13 0 .
1
0
2
Учитывая следствие, система имеет
единственное тривиальное решение.
13.
п.3. Фундаментальная система решенийРассмотрим однородные системы линейных
уравнений с бесконечным количеством
решений.
r(A) r n
14.
Теорема 2.Пусть
x1
x1
x2
x2
e1
, e2
...
...
xn
xn
ꟷ решения однородной системы.
Тогда С 1
С 1 e1 , e1 e 2
ꟷ также решения этой однородной системы.
15.
Замечание.Любая линейная комбинация решений
однородной системы также является
решением этой системы.
Система линейно независимых решений
e 1 , e 2 , ...e k
называется фундаментальной, если каждое
решение системы является линейной
комбинацией решений e 1 , e 2 , ... e k .
Неопределенная система однородных
уравнений имеет бесконечное множество
фундаментальных систем.
16.
Теорема 3.Пусть ранг матрицы коэффициентов
однородной системы меньше числа
переменных,
r ( A ) r n.
Тогда всякая фундаментальная система
решений состоит из n r векторов.
17.
Общее решение однородной системы можнозаписать в виде
c1e1 c2 e2 ... ck ek ,
где e 1 , e 2 , ...e k ꟷ фундаментальная система
решений этой системы, c1 , c2 ,..., ck , k n r .
18.
Пример.3 x1 6 x2 9 x3 13 x4 0,
x1 2 x2 x3 x4 0,
x 2 x 2 x 3 x 0.
2
3
4
1
Решение.
1 2 2 3 0 1 2 2 3 0
1 2 1 1 0 ~ 0 0 3 4 0 ~
3 6 9 13 0 0 0 3 4 0
1 2 2 3 0
~
0 3 4 0
0
19.
1 2 2 3 00 3 4 0
0
r 2 ꟷ количество базисных переменных
n r 4 2 2 ꟷ количество свободных
переменных
(количество векторов в ФСР)
x1 , x 3 ꟷ базисные
x 2 , x 4 ꟷ свободные
x1 x3 x2 x4
1 2 2 3
0 3 0 4
20.
c1 c2x1 x3 x2 x4
1
1 2 2 3 1 0 2
1 2 2 3
3
4 ~
~
0 3 0 4 0 1 0 0 1 0 4
3
3
1
4
x1 2 c1 c 2 , x 2 c1 , x 3 c 2 , x 4 c 2
3
3
ꟷ общее решение однородной системы
21.
Найдем фундаментальную систему решений.1
4
x1 2 c1 c 2 , x 2 c1 , x 3 c 2 , x 4 c 2
3
3
c 1 1, c 2 0 :
x 1 2 , x 2 1, x 3 0 , x 4 0
c1 0 , c 2 1 :
1
4
x1 , x 2 0, x 3 , x 4 1
3
3
2
1 / 3
1
0
e1
, e2
ꟷ фундаментальная
0
4 / 3
система решений
1
0
22.
Общее решение однородной системы:2
1 / 3
1
0
, c , c
X c1e1 c2 e2 c1 c2
1 2
0
4 / 3
0
1
23.
Теорема 4.Общее решение неоднородной системы
линейных уравнений равно сумме общего
решения соответствующей однородной
системы и произвольного частного решения
неоднородной системы.
24.
x1 2 x2 x3 3 x4 0,x1 2 x2 2 x3 x4 3,
3 x1 6 x2 5 x4 3,
4 x1 8 x2 x3 x4 3.
а) найти общее решение;
б) используя результат предыдущего пункта,
найти общее решение соответствующей
однородной системы и записать его в
векторной форме.
Пример.
25.
Решение.1
1
3
4
2 1 3 0 1
2 2 1 3 0
~
2 2 1 3 0
8 1 1 3 0
1 2 1 3 0
~
0 0 3 4 3
2 1 3 0
0 3 4 3
~
0 3 4 3
0 3 4 3
26.
1 2 1 3 00 0 3 4 3
r 2 ꟷ количество базисных переменных
n r 4 2 2 ꟷ количество свободных
переменных
(количество векторов в ФСР)
x1 , x 3 ꟷ базисные
x 2 , x 4 ꟷ свободные
x2 x4
x1 x3
1 1 0 2 3
0 3 3 0 4
27.
1 1 0 2 31 1 0 2 3
~
~
4
0 3 3 0 4 0 1 1 0
3
5
1 0 1 2 3
~
4
0 1 1 0
3
28.
c2x1 x3
x4
5
1 0 1 2 3
4
0 1 1 0
3
c1
x2
5
4
x1 1 2 c1 c 2 , x 2 c1 , x 3 1 c 2 , x 4 c 2
3
3
ꟷ общее решение неоднородной системы
29.
54
x1 1 2 c1 c 2 , x 2 c1 , x 3 1 c 2 , x 4 c 2
3
3
Частное решение неоднородной системы:
c1 0 , c 2 0 :
x 1 1, x 2 0 , x 3 1, x 4 0
x он x оо xчн ,
x оо x он xчн
5
4
x1 2 c1 c 2 , x 2 c1 , x 3 c 2 , x 4 c 2
3
3
ꟷ общее решение однородной системы
30.
Найдем фундаментальную систему решений.5
4
x1 2 c1 c 2 , x 2 c1 , x 3 c 2 , x 4 c 2
3
3
c 1 1, c 2 0 :
x 1 2 , x 2 1, x 3 0 , x 4 0
c1 0 , c 2 1 :
5
4
x1 , x 2 0, x3 , x 4 1
3
3
2
5 / 3
1
0
e1
e2
ꟷ фундаментальная
0
4/3
система решений
0
1
31.
Общее решение однородной системы:2
5 / 3
1
0
, c , c
xоо c1e1 c2 e2 c1 c2
0
4/3 1 2
0
1
Общее решение неоднородной системы:
2
5 / 3 1
1
0
0
, c , c
xон xоо xчн c1 c2
0
4 / 3 1 1 2
0
1 0




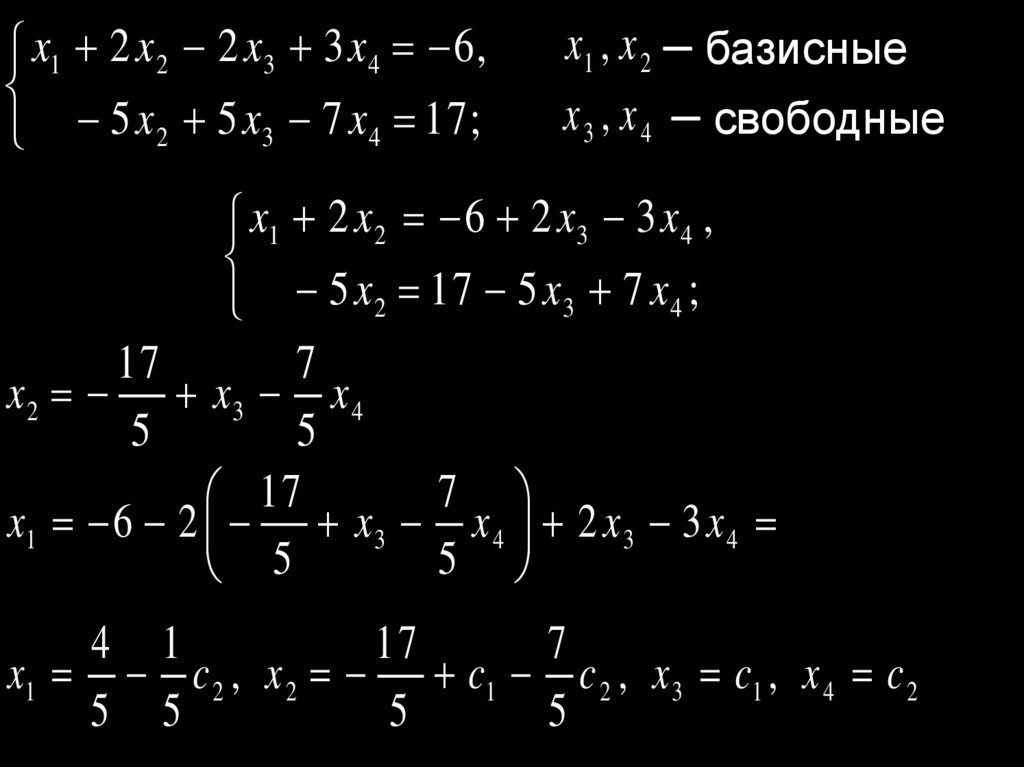

























 Математика
Математика








