«Электротехника» и «теоретические основы электротехники»

1.

1
«ЭЛЕКТРОТЕХНИКА» И
«ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ЭЛЕКТРОТЕХНИКИ»
Кафедра ФМПК, ФТИ УрФУ

2.

2
6 Переходные процессы
6.1 Установившиеся и переходные процессы.
Законы коммутации

3.

Установившейся режим
3
6.1 Установившиеся и переходные процессы. Законы коммутации
Установившимся режимом называется такой
режим, при котором токи и напряжения в цепи
являются
постоянными
величинами
или
периодическими функциями времени.
Режим покоя, когда все токи и напряжения в цепи
равны нулю также считается установившимся.
В установившемся режиме каждый ток или
напряжение имеет постоянную величину (режим
постоянного тока) или постоянную амплитуду, частоту
и начальную фазу (режим гармонического тока).

4.

Переходный процесс
4
6.1 Установившиеся и переходные процессы. Законы коммутации
Переходным процессом называется режим, при
котором токи и напряжения в цепи изменяются от
одних установившихся значений до других.
Во время переходного процесса токи и
напряжения в цепи не могут быть постоянными или
периодическими.
Задача
анализа
переходных
процессов
заключается в определении переходных токов и
напряжений как функций времени.

5.

Причины переходных процессов
5
6.1 Установившиеся и переходные процессы. Законы коммутации
При
изменении
действующих
в
электрической цепи задающих функций
источников питания
При изменении параметров самой цепи
– включение / отключение источника
– короткое замыкание участка цепи
Коммутация – процесс скачкообразного
(мгновенного)
изменения
какого-либо
параметра электрической цепи

6.

Идеальный ключ
6
6.1 Установившиеся и переходные процессы. Законы коммутации
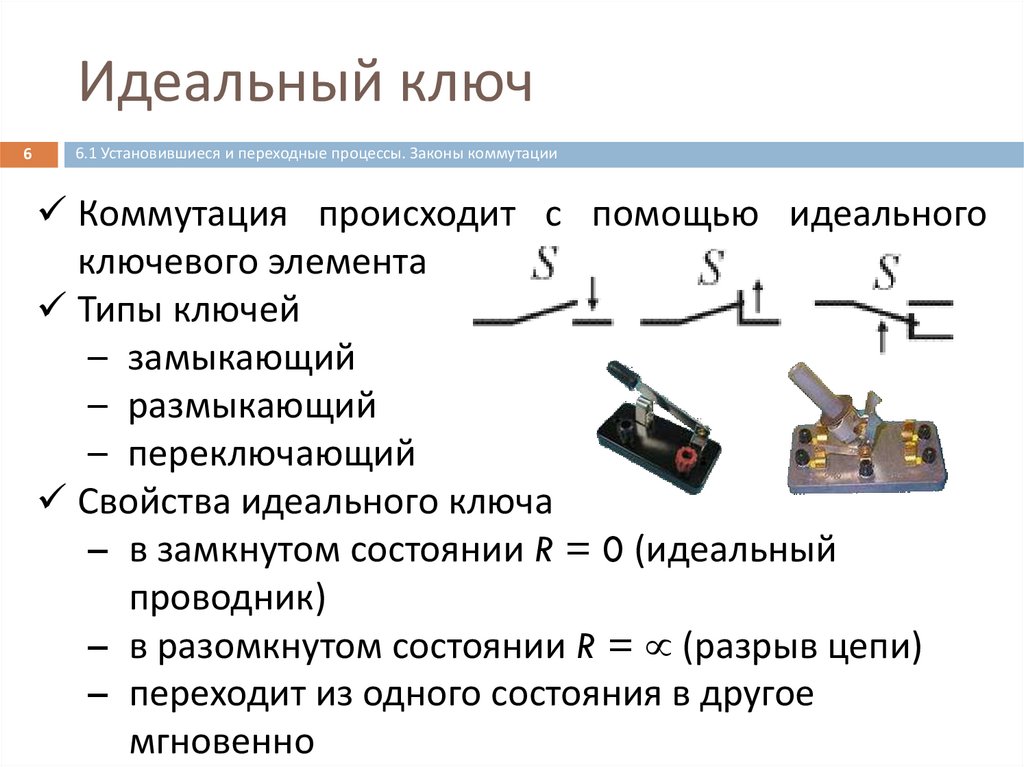
Коммутация происходит с помощью идеального
ключевого элемента
Типы ключей
– замыкающий
– размыкающий
– переключающий
Свойства идеального ключа
– в замкнутом состоянии R = 0 (идеальный
проводник)
– в разомкнутом состоянии R = (разрыв цепи)
– переходит из одного состояния в другое
мгновенно

7.

Моменты коммутации
7
6.1 Установившиеся и переходные процессы. Законы коммутации
t = 0 – момент коммутации
t = 0 – – последний момент перед коммутацией
t = 0+ – первый момент после коммутации
Установившийся
режим
Переходный
процесс
0- 0 0+
Установившийся
режим
t
Переходный процесс занимает некоторое время
(теоретически бесконечно большое)

8.

Энергия в электрической цепи
8
6.1 Установившиеся и переходные процессы. Законы коммутации
Установившийся режим характеризуется определенным
запасом энергии магнитного и электрического полей
Lk ik2 t
Cl ul2 t
W
2
2
k
l
ik – мгновенный ток в катушке Lk
ul – мгновенное напряжение на конденсаторе Cl
k и l – индексы суммирования
В переходном режиме происходит изменение запасенной в
цепи энергии и это изменение не может происходить
скачкообразно. Для мгновенного изменение энергии
требуется бесконечно большая мощность P = dW/dt в
электрической цепи, что лишено физического смысла

9.

Законы коммутации
9
6.1 Установившиеся и переходные процессы. Законы коммутации
Ток в любом индуктивном элементе является
непрерывной функцией времени и не может
изменяться скачком (для момента коммутации t = 0)
iL(0+) = iL(0-) = iL(0)
Напряжение на любом емкостном элементе
является непрерывной функцией времени и не
может
изменяться
скачком
(для
момента
коммутации t = 0)
uC(0+) = uC(0-) = uC(0)

10.

Выводы
10
6.1 Установившиеся и переходные процессы. Законы коммутации
iL и uC в начальный момент после коммутации имеют
те же значения, что и перед коммутацией и затем
плавно изменяются
iR и uR, а также iC и uL могут изменяться мгновенно

11.

11
6 Переходные процессы
6.2 Общий подход к анализу переходных
процессов

12.

Анализ переходных процессов
12
6.2 Общий подход к анализу переходных процессов
Задача заключается в определении мгновенных
значений токов и напряжений в любой момент
после коммутации
Задача сводится к решению дифференциального
уравнения
d y
d 1 y
dy
a a 1 1 ... a1 a0 y f t
dt
dt
dt
f(t) – воздействие на электрическую цепь
y(t) – отклик на воздействие

13.

Решение задачи
13
6.2 Общий подход к анализу переходных процессов
Определение начальных условий
y 0 , y 0 ,..., y 1 0
из законов коммутации
iL 0 iL 0 iL 0
uC 0 uC 0 uC 0
Решение дифференциального уравнения
– классическим методом
– операторным методом

14.

14
6 Переходные процессы
6.2 Общий подход к анализу переходных
процессов
6.2.1 Классический метод анализа

15.

Суть метода
15
6.2.1 Классический метод анализа
Метод основан на составлении системы дифференциальных
и алгебраических уравнений с использованием уравнений
для элементов и законов Кирхгофа для мгновенных токов и
напряжений в цепи
duC t
diL t
iC t C
, uL t L
, uR t RiR t , ik t 0, ul t 0
dt
dt
k
l
Для определения интересующей реакции систему исходных
уравнений путем исключения остальных переменных
приводят к одному линейному дифференциальному
уравнению -го порядка с постоянными коэффициентами
d y
d 1 y
dy
a a 1 1 ... a1 a0 y f t
dt
dt
dt

16.

Вид решения ЛДУ
16
6.2.1 Классический метод анализа
y t yСВ t yПР t
yСВ(t) – свободная или собственная составляющая –
это общее решение соответствующего однородного ДУ
цепи, которое получается при f(t) = 0 (в цепи
отсутствует внешнее воздействие, т.е. источник)
yПР(t)
–
принужденная
или
вынужденная
составляющая – это частное решение ДУ цепи,
которое находится при анализе установившегося
режима в цепи после коммутации и определяется
воздействием f(t)

17.

Свободная составляющая
17
6.2.1 Классический метод анализа
определяется свойствами самой цепи
существует во время переходного процесса
yСВ(t) 0 при t y(t) yПР(t)
Характеристическое уравнение
1
a p a 1 p
yСВK t AK e PK t
... a1 p a0 0
1
PK – корни уравнения
AK – постоянные интегрирования
yСВ t A1 A2t ... Ant n 1 e PK t
для корней кратности n

18.

Принужденная составляющая
18
6.2.1 Классический метод анализа
вид частного
воздействия
решения
определяется
видом
– если f(t) = const, то yПР(t) = const
– если f(t) = f(Аin, in, sin( t)), то yПР(t) = f(Аout, out, sin( t))
обусловлена воздействием источников в цепи
y(t) yПР(t) при t
принужденная
составляющая
называется
установившейся yПР(t) = yУСТ(t)
– установившееся значение (в случае постоянной
вынуждающей силы)
– установившаяся функция (в случае гармонической
вынуждающей силы)

19.

Этапы расчета
19
6.2.1 Классический метод анализа
1. Анализ цепи до коммутации
Определяются токи через индуктивности и напряжения на
емкостях в последний момент перед коммутацией.
2. Определение независимых начальных условий
В соответствии с законами коммутации определяются токи
через индуктивности и напряжения на ёмкостях в первый
момент после коммутации.
3. Составление ДУ цепи после коммутации
Составляется система уравнений электрического равновесия
для цепи после коммутации. Методом последовательного
исключения неизвестных система сводится к одному
дифференциальному уравнению цепи.

20.

Этапы расчета (продолжение)
20
6.2.1 Классический метод анализа
4. Определение свободной составляющей
По дифференциальному уравнению цепи определяется
характеристическое уравнение, находятся корни этого
уравнения и с точностью до постоянных интегрирования
определяется свободная составляющая
5. Определение принужденной составляющей
Анализируется цепь для установившегося режима после
коммутации
6. Запись общего вида решения ДУ
7. Определение постоянных интегрирования
Использование начальных условий
8. Нахождение решения ДУ
Подстановка постоянных интегрирования

21.

21
6 Переходные процессы
6.2 Общий подход к анализу переходных
процессов
6.2.1 Классический метод анализа
6.2.2 Переходные процессы в RL-цепи

22.

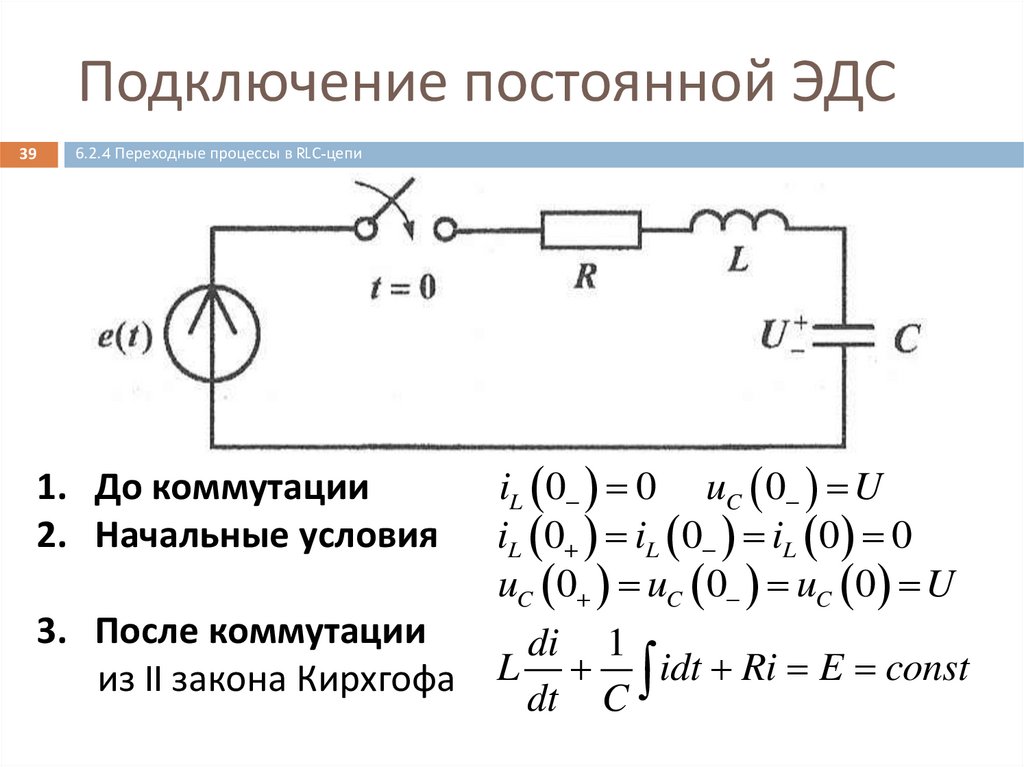
Подключение постоянной ЭДС
22
6.2.2 Переходные процессы в RL-цепи
До
После
1. До коммутации
iL 0 0
2. Начальные условия iL 0 iL 0 iL 0 0
3. После коммутации
di
из II закона Кирхгофа U L U R E; L Ri E
dt

23.

Анализ RL-цепи (продолжение)
23
6.2.2 Переходные процессы в RL-цепи
4. Определение свободной составляющей
Характеристическое уравнение LP R 0
L
Корень P R L
постоянная
t
R
t
R
L
времени ЭЦ
iСВ t Ae Ae
Постоянная времени – это время, в течение
которого
свободная
составляющая
процесса
уменьшается в е 2,72 раз по сравнению с начальным
значением.
Определяет скорость протекания переходного процесса: чем
меньше постоянная времени, тем быстрее заканчивается
переходный процесс.

24.

Анализ RL-цепи (продолжение)
24
6.2.2 Переходные процессы в RL-цепи
5. Определение принужденной составляющей
Анализ режима по постоянному току для установившегося
режима после коммутации
E
iПР t
R
6. Запись общего вида решения ДУ
t
E
i t iСВ t iПР t Ae
R
7. Определение постоянных интегрирования
0
E
E
i 0 0
0 Ae A
R
R

25.

Анализ RL-цепи (продолжение)
25
6.2.2 Переходные процессы в RL-цепи
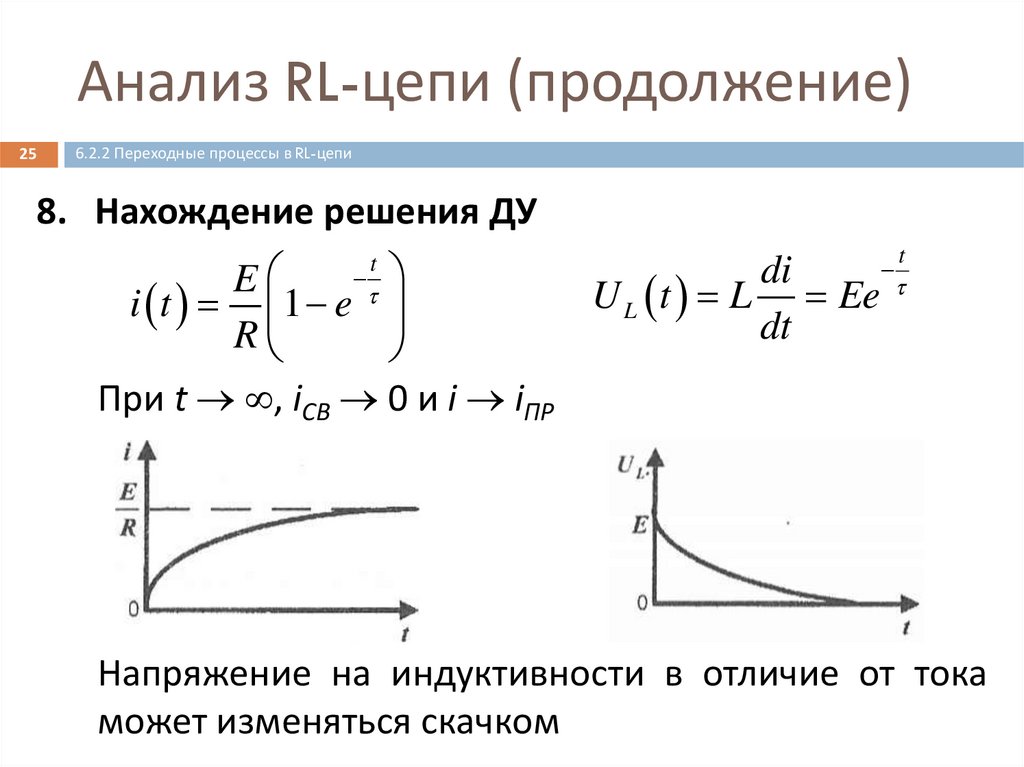
8. Нахождение решения ДУ
E
i t 1 e
R
t
t
di
U L t L Ee
dt
При t , iСВ 0 и i iПР
Напряжение на индуктивности в отличие от тока
может изменяться скачком

26.

Подключение гармонической ЭДС
26
6.2.2 Переходные процессы в RL-цепи
e t Em cos t
1. До коммутации
iL 0 0
2. Начальные условия iL 0 iL 0 iL 0 0
3. После коммутации
di
из II закона Кирхгофа U L U R e t ; L Ri e t
dt

27.

Анализ RL-цепи (продолжение)
27
6.2.2 Переходные процессы в RL-цепи
4. Определение свободной составляющей
Характеристическое уравнение LP R 0
L
Корень P R L
постоянная
t
R
t
R
L
времени ЭЦ
iСВ t Ae Ae
5. Определение принужденной составляющей
Используется метод комплексных амплитуд
Em
iПР t
cos t
2
2
R L
L
arctg
R

28.

Анализ RL-цепи (продолжение)
28
6.2.2 Переходные процессы в RL-цепи
6. Запись общего вида решения ДУ
i t iСВ t iПР t
Em
t
cos t Ae
R L
7. Определение постоянных интегрирования
Em
0
cos A
i 0 0
2
2
R L
2
2
A
Em
R 2 L
2
cos

29.

Анализ RL-цепи (продолжение)
29
6.2.2 Переходные процессы в RL-цепи
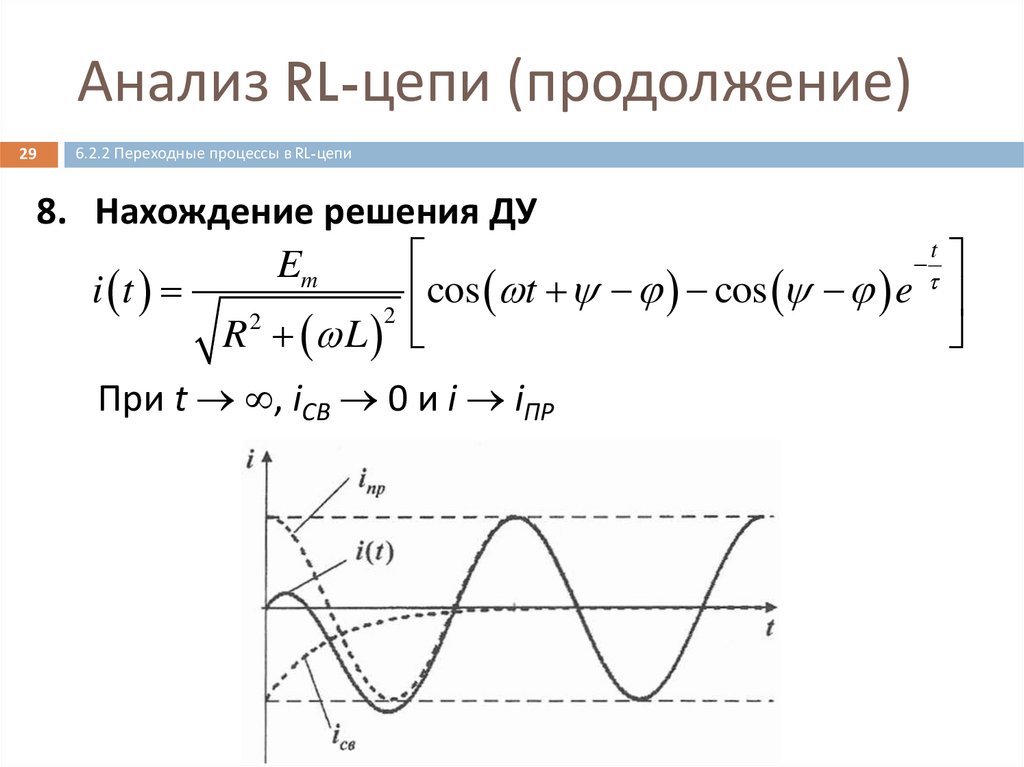
8. Нахождение решения ДУ
t
Em
i t
cos
t
cos
e
2
2
R L
При t , iСВ 0 и i iПР

30.

30
6 Переходные процессы
6.2 Общий подход к анализу переходных
процессов
6.2.1 Классический метод анализа
6.2.2 Переходные процессы в RL-цепи
6.2.3 Переходные процессы в RС-цепи

31.

Подключение постоянной ЭДС
31
6.2.3 Переходные процессы в RС-цепи
1. До коммутации
uС 0 U
2. Начальные условия uC 0 uC 0 uC 0 U
3. После коммутации
dU C
E
из II закона Кирхгофа U C U R E; U C RC
dt

32.

Анализ RС-цепи (продолжение)
32
6.2.3 Переходные процессы в RС-цепи
4. Определение свободной составляющей
Характеристическое уравнение RCP 1 0
1
Корень
P
RC постоянная
RC
t
времени ЭЦ
pt
uCСВ t Ae Ae
5. Определение принужденной составляющей
Анализ режима по постоянному току для установившегося
режима после коммутации
uСПР t E

33.

Анализ RС-цепи (продолжение)
33
6.2.3 Переходные процессы в RС-цепи
6. Запись общего вида решения ДУ
t
uC t E Ae
7. Определение постоянных интегрирования
uC 0 U
0
U E Ae A U E
t
8. Нахождение решения ДУ
uC t E U E e
E>U
E<U

34.

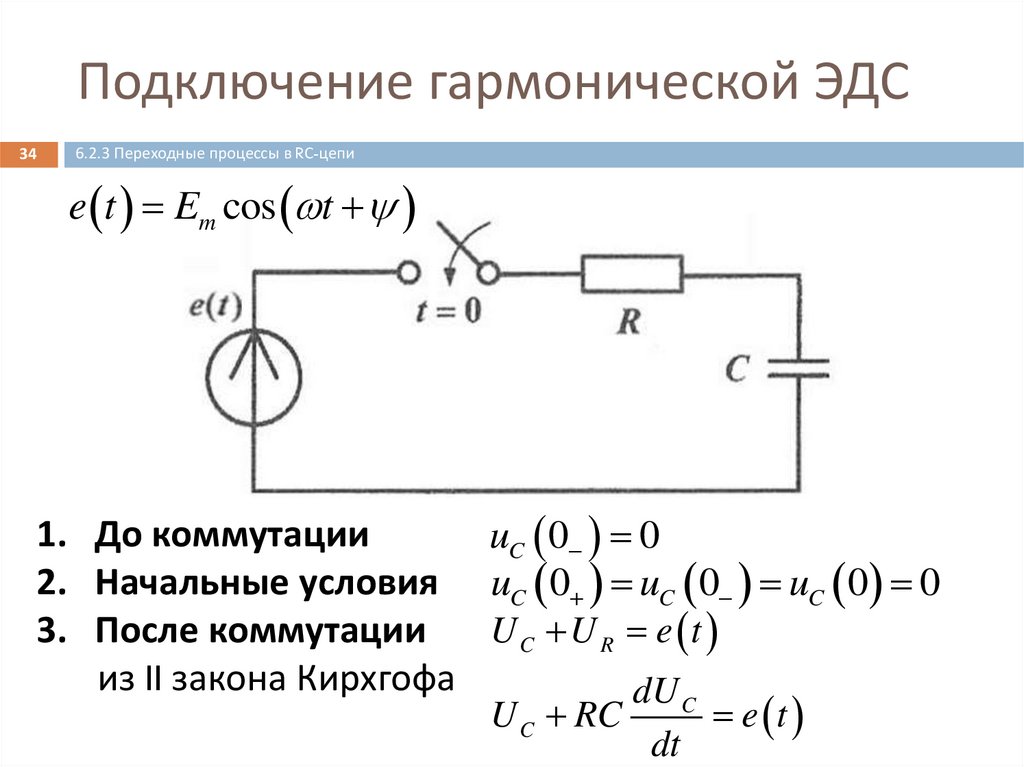
Подключение гармонической ЭДС
34
6.2.3 Переходные процессы в RС-цепи
e t Em cos t
1. До коммутации
uC 0 0
2. Начальные условия uC 0 uC 0 uC 0 0
3. После коммутации
UC U R e t
из II закона Кирхгофа
dU
U C RC
C
dt
e t

35.

Анализ RС-цепи (продолжение)
35
6.2.3 Переходные процессы в RС-цепи
4. Определение свободной составляющей
Характеристическое уравнение RCP 1 0
Корень P 1 RC
постоянная
RC
t
pt
времени ЭЦ
uCСВ t Ae Ae
5. Определение принужденной составляющей
Используется метод комплексных амплитуд
Im
Em
uCПР t
cos t I m
2
C
2
1
2
R
1
C
arctg
СR

36.

Анализ RС-цепи (продолжение)
36
6.2.3 Переходные процессы в RС-цепи
6. Запись общего вида решения ДУ
Im
uС t
cos t Ae
C
2
t
7. Определение постоянных интегрирования
Im
0
cos A
uC 0 0
C
2
Im
Im
A
cos
sin
C
2 C

37.

Анализ RС-цепи (продолжение)
37
6.2.3 Переходные процессы в RС-цепи
8. Нахождение решения ДУ
t
Im
uC t
cos t sin e
C
2
duC t
iС t С
dt

38.

38
6 Переходные процессы
6.2 Общий подход к анализу переходных
процессов
6.2.1 Классический метод анализа
6.2.2 Переходные процессы в RL-цепи
6.2.3 Переходные процессы в RС-цепи
6.2.4 Переходные процессы в RLС-цепи

39.

Подключение постоянной ЭДС
39
6.2.4 Переходные процессы в RLС-цепи
1. До коммутации
2. Начальные условия
3. После коммутации
из II закона Кирхгофа
iL 0 0 uC 0 U
iL 0 iL 0 iL 0 0
uC 0 uC 0 uC 0 U
di 1
L idt Ri E const
dt C

40.

Анализ RLС-цепи (продолжение)
40
6.2.4 Переходные процессы в RLС-цепи
4. Определение свободной составляющей
1
2
Характеристическое уравнение Lp Rp 0
C
2
Корни
R
1
R
p1,2
2L
2 L LC
или
где
p1,2 2 02
0
1
частота резонанса
LC
R
2L
коэффициент затухания

41.

Анализ RLС-цепи (продолжение)
41
6.2.4 Переходные процессы в RLС-цепи
5. Определение принужденной составляющей
Анализ режима по постоянному току
установившегося режима после коммутации
iПР t 0
6. Запись общего вида решения ДУ
i t iСВ t iПР t A1e p1t A2e p2t
для

42.

Анализ RLС-цепи (продолжение)
42
6.2.4 Переходные процессы в RLС-цепи
7. Определение постоянных интегрирования
iL 0 0 A1 A2 0
A1 A2
E U
E U
uC 0 U A1 p1 A2 p2
L
2 L 2 02
di 0
т.к. di t
A1 p1 A2 p2
dt t 0
dt
di 0
di 0 E U
L
uC 0 E
dt
dt
L

43.

Анализ RLС-цепи (продолжение)
43
6.2.4 Переходные процессы в RLС-цепи
8. Нахождение решения ДУ
i t
E U
e p1t e p2t
2
2 L 2 0
– Апериодический ( > 0, p1и p2 R)
i t
E U
e p1t e p2t
2
2 L 2 0
– Критический ( = 0, p1= p2 = - R)
E U t
E U
pt
i t
te , т.к. i t A1 A2t e , где A1 0; A2
L
L
– Колебательный ( < 0, p1= p2 =- ± j СВ С)
E U t
i t
e sin СВ t
L СВ

44.

Анализ RLС-цепи (продолжение)
44
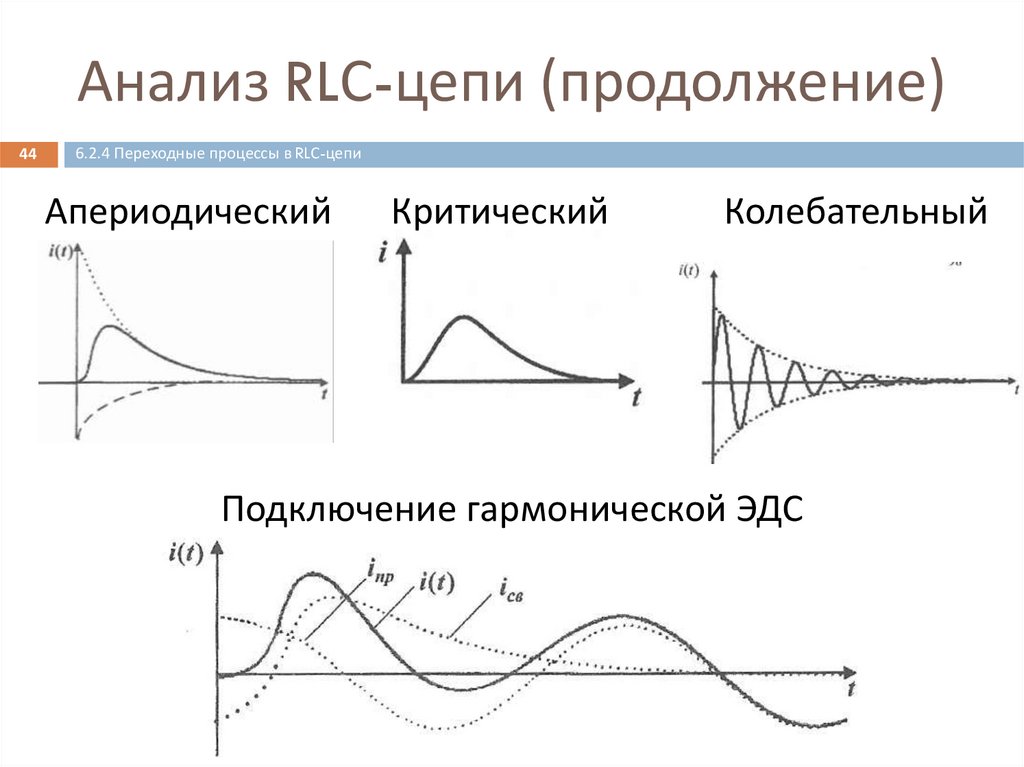
6.2.4 Переходные процессы в RLС-цепи
Апериодический
Критический
Колебательный
Подключение гармонической ЭДС

45.

45
6 Переходные процессы
6.2 Общий подход к анализу переходных
процессов
6.2.5 Операторный метод анализа

46.

Преобразование Лапласа
46
6.2.5 Операторный метод анализа
Прямое преобразование
A p L a t e pt a t dt
a t ke 0t
0
A(p) – операторное изображение функции a(t)
k и 0 – вещественные числа
Обратное преобразование
0 j
1
1
pt
a t L A p
A p e dp
2 j 0 j
a(t) – оригинал
a t
A p

47.

Свойства преобразования Лапласа
47
6.2.5 Операторный метод анализа
Свойство
линейности
n
n
k a t k A p , a t
i 1
i i
i 1
i
i
i
Ai p
Теорема дифференцирования Теорема подобия
da t
1 p
a t
A
pA p a 0
dt
Теорема интегрирования Теорема запаздывания
x
A p
pt0
a
t
t
e
A p
a
t
dt
0
0
p
Теорема смещения
Теорема свертывания
x
e t a t
A p
a a t d
1
0
2
A1 p A2 p

48.

Свойства преобразования Лапласа
48
6.2.5 Операторный метод анализа
Предельные соотношения
lim a t
t 0
lim pA p
p
lim a t lim pA p
t
p 0
Теорема разложения
N p an p n an 1 p n 1 ... a1 p a0
A p
M p bm p m bm 1 p m 1 ... b1 p b0
pk – простые корни знаменателя
n
N pk
N p
pk t
A p
e
M p k 1 dM p
dp p p
k

49.

Изображения некоторых функций
49
6.2.5 Операторный метод анализа

50.

50
Уравнения равновесия цепи в
операторной форме
6.2.5 Операторный метод анализа
Первый закон Кирхгофа
I p 0
k
k
Второй закон Кирхгофа
U p E p
n
n
m
m
U p
Z p
– операторное
I p
сопротивление
1
Y p
– операторная
Z p
проводимость
Операторным сопротивлением называется отношение
операторного изображения напряжения к операторному
изображению тока при нулевых начальных условиях

51.

Операторная схема замещения R
51
6.2.5 Операторный метод анализа
Эквивалентная схема
сопротивления
Операторная схема
замещения сопротивления
U R p RI R p
uR t RiR t
iR t GuR t
1
G
R
I R p GU R p
ZR p
YR p
UR p
IR p
IR p
UR p
R
1
G
R

52.

Операторная схема замещения C
52
6.2.5 Операторный метод анализа
Эквивалентная схема емкости
iC t C
duC t
dt
Операторная схема
замещения емкости
с источником тока
с источником ЭДС
t
1
uC t uC 0 iC d
C0
IC p
pC
UC p
I C p pCU C p CuC 0
YC p
uC 0 I C p
UC p
p
pC
При uC 0 0
I C p pCU C p
UC p
IC p
pC
ZC p
UC p
1
I C p pC

53.

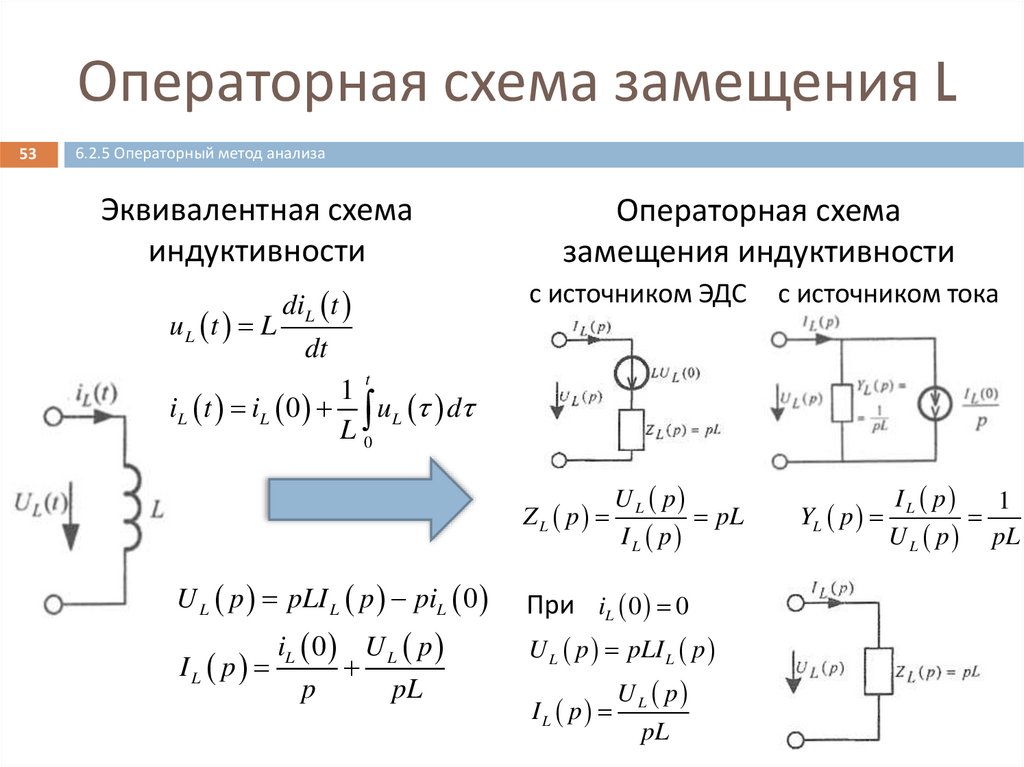
Операторная схема замещения L
53
6.2.5 Операторный метод анализа
Эквивалентная схема
индуктивности
di t
uL t L L
dt
t
1
iL t iL 0 u L d
L0
Операторная схема
замещения индуктивности
с источником ЭДС
ZL p
U L p pLI L p piL 0
i 0 U L p
IL p L
p
pL
UL p
pL
IL p
При iL 0 0
U L p pLI L p
IL p
UL p
pL
с источником тока
YL p
IL p
1
U L p pL

54.

Схема применения метода
54
6.2.5 Операторный метод анализа
1. Анализ цепи до коммутации. Определение независимых
начальных условий
2. Составление
операторной
эквивалентной
электрической цепи после коммутации
схемы
3. Составление системы уравнений электрического равновесия
цепи в операторной форме
4. Решение уравнений электрического равновесия цепи
относительно изображений искомых токов и напряжений
5. Определение оригиналов искомых токов и напряжений

55.

Анализ последовательной RC-цепи
55
6.2.5 Операторный метод анализа
1. Анализ
цепи
до
коммутации. Определение
независимых начальных
условий
uC 0 uC 0 uC 0 U
2. Составление операторной
схемы замещения цепи
после коммутации

56.

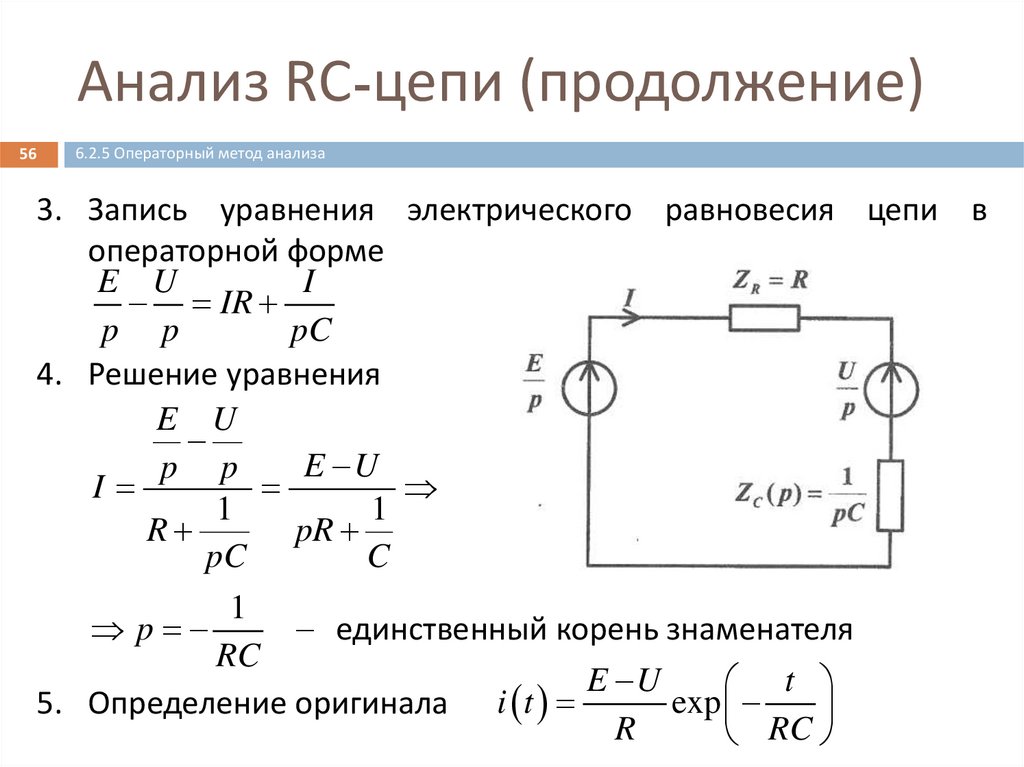
Анализ RС-цепи (продолжение)
56
6.2.5 Операторный метод анализа
3. Запись уравнения электрического равновесия цепи в
операторной форме
E U
I
IR
p p
pC
4. Решение уравнения
E U
E U
p p
I
1
1
R
pR
pC
C
1
единственный корень знаменателя
p
RC
E U
t
exp
5. Определение оригинала i t
R
RC

57.

Анализ последовательной RL-цепи
57
6.2.5 Операторный метод анализа
1. Анализ
цепи
до
коммутации. Определение
независимых начальных
условий
iL 0 iL 0 iL 0 0
2. Составление операторной
схемы замещения цепи
после коммутации
LiL 0
Z L pL

58.

Анализ RL-цепи (продолжение)
58
6.2.5 Операторный метод анализа
3. Запись уравнения электрического равновесия цепи в
операторной форме
E
LiL 0 I p R I p pL
p
4. Решение уравнения
E
R
I p
p1 0; p2
корни знаменателя
p Lp R
L
N p
I p
M p
N pk
dM p
e
pk t
k
dp
p pk
5. Определение оригинала
t
E 0t E RL t E
i t e e 1 e
R
R
R
N p1 N p2 E
dM p
2 Lp1 R R
dp p p
1
dM p
2 Lp2 R R
dp p p
2

59.

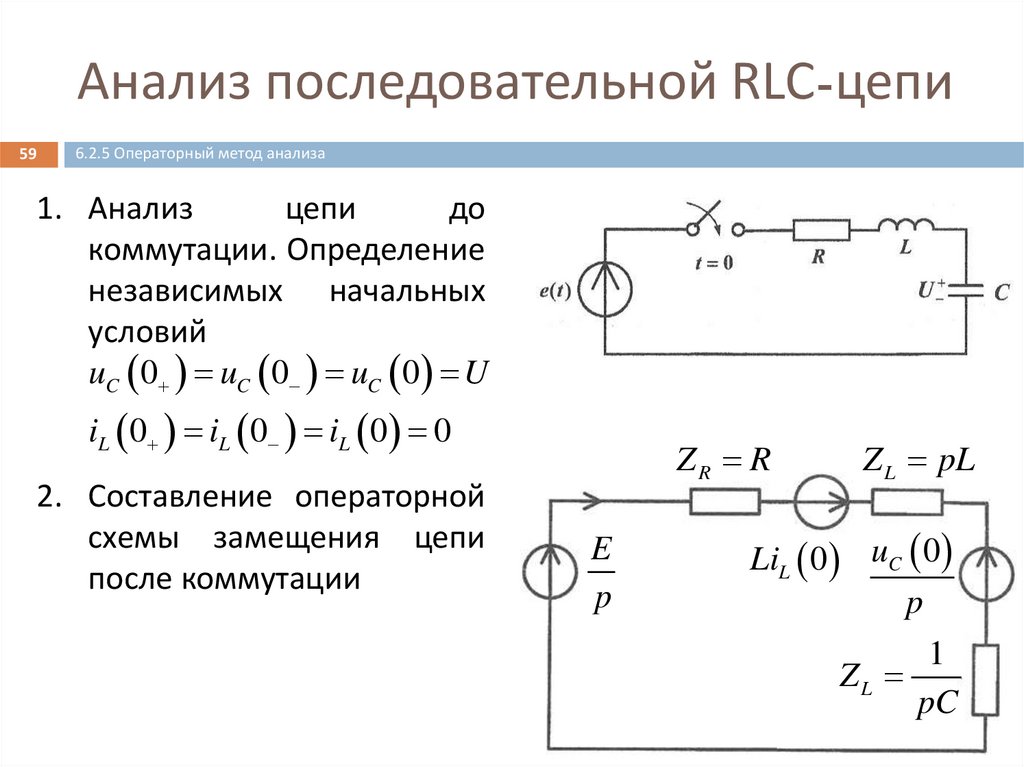
Анализ последовательной RLC-цепи
59
6.2.5 Операторный метод анализа
1. Анализ
цепи
до
коммутации. Определение
независимых начальных
условий
uC 0 uC 0 uC 0 U
iL 0 iL 0 iL 0 0
2. Составление операторной
схемы замещения цепи
после коммутации
ZR R
E
p
Z L pL
LiL 0 uC 0
p
1
ZL
pC

60.

Анализ RLС-цепи (продолжение)
60
6.2.5 Операторный метод анализа
3. Запись уравнения электрического равновесия цепи в
операторной форме
I p
E uC 0
LiL 0 I p R I p pL
p
p
pC
4. Решение уравнения
E U
C E U
N ( p)
p p
I p
2
1
LCp RCp 1 M ( p )
R pL
pC
p1,2 2 02 корни знаменателя
R
коэффициент
2L
затухания
0
1
частота
LC
резонанса

61.

Режимы работы RLC-цепи
61
6.2.5 Операторный метод анализа
5. Определение оригинала
– Апериодический ( > 0, p1и p2 R)
N p
N pk
A p
M p k dM p
dp
i t
E U
dM p
2 LCp1,2 R
dp p p
p pk
1,2
e e
p1t
2 L 2 02
N p1 N p2 C E U
e pk t
p2t
– Критический ( = 0, p1= p2 = - R)
I p
E U
L p
i t
2
E U t
te
L
– Колебательный ( < 0, p1= p2 =- ± j СВ С)
I t
E U
2L
2
2
0
e p1t e p2t
E U t j СВt j СВt
E U t
e e
e
e sin СВt
2 L СВ
2 L СВ

62.

Эквивалентные операторные схемы
62
6.2.5 Операторный метод анализа
Источники тока и напряжений i(t) и u(t) заменяются
соответствующими изображениями I(p) и U(p)
Сопротивление R заменяется на R
При нулевых начальных условиях:
индуктивность L заменяется на pL
емкость С заменяется на 1/pC
При не нулевых начальных условиях
индуктивность L заменяется на
pL с источником напряжения Li(0)
емкость С заменяется на 1/pC
с источник напряжения uC(0)/р

63.

Преимущества
63
6.2.5 Операторный метод анализа
простота
отсутствие громоздких операций по определению
постоянных интегрирования
можно рассчитать переходный процесс любым из
ранее рассмотренных методов:
контурных токов
узловых напряжений
и др.

64.

Операторные характеристики
64
6.2.5 Операторный метод анализа
Операторной характеристикой линейной электрической
цепи называется отношение операторного изображения
реакции цепи к операторному изображению воздействия при
нулевых начальных условиях
H nm p
Yn p
X m p
xm t
X m p воздействие
yn t Yn p
реакция
Комплексную частотную характеристику (КЧХ) можно
рассматривать как частный случай операторной при Re(p) = 0

65.

Виды операторных характеристик
65
6.2.5 Операторный метод анализа
Операторный коэффициент передачи по напряжению
u1 t U1 p воздействие
U2 p
KU p
u2 t U 2 p реакция
U1 p
Операторный коэффициент передачи по току
i1 t I1 p воздействие
I2 p
KI p
I1 p
i2 t I 2 p реакция
Операторное сопротивление
U p
Z p
I p
Операторная проводимость
I p
Y p
U p

66.

Нули и полюса
66
6.2.5 Операторный метод анализа
Любая операторная характеристика линейной электрической
цепи, не содержащей независимых источников энергии,
является рациональной функцией переменной р с
вещественными коэффициентами
N p an p n an 1 p n 1 ... a1 p a0
H nm p
M p bm p m bm 1 p m 1 ... b1 p b0
Нули р0i – значения р, при которых N(р0i)=0, M(р0i) 0
Полюса рxi – значения р, при которых N(рxi) 0, M(рxi)=0
an
масштабный коэффициент
K
bm

67.

Полюсно-нулевая диаграмма
67
6.2.5 Операторный метод анализа
Нули и полюса характеризуют Hnm(p) с точностью до постоянного
множителя K. По ним можно найти реакцию цепи на заданное
воздействие
H nm p
xm t
Yn p
X m p
X m p воздействие
yn t Yn p
реакция

68.

68
6 Переходные процессы
6.2 Общий подход к анализу переходных
процессов
6.2.6 Метод наложения (интегралы
наложения)

69.

Применение принципа
69
6.2.6 Метод наложения
Пусть внешнее воздействие x(t)
представлено
в
виде
взвешенной суммы некоторых
элементарных воздействий
x t k xk t
По принципу суперпозиции
отклик электрической цепи y(t)
y t k yk t

70.

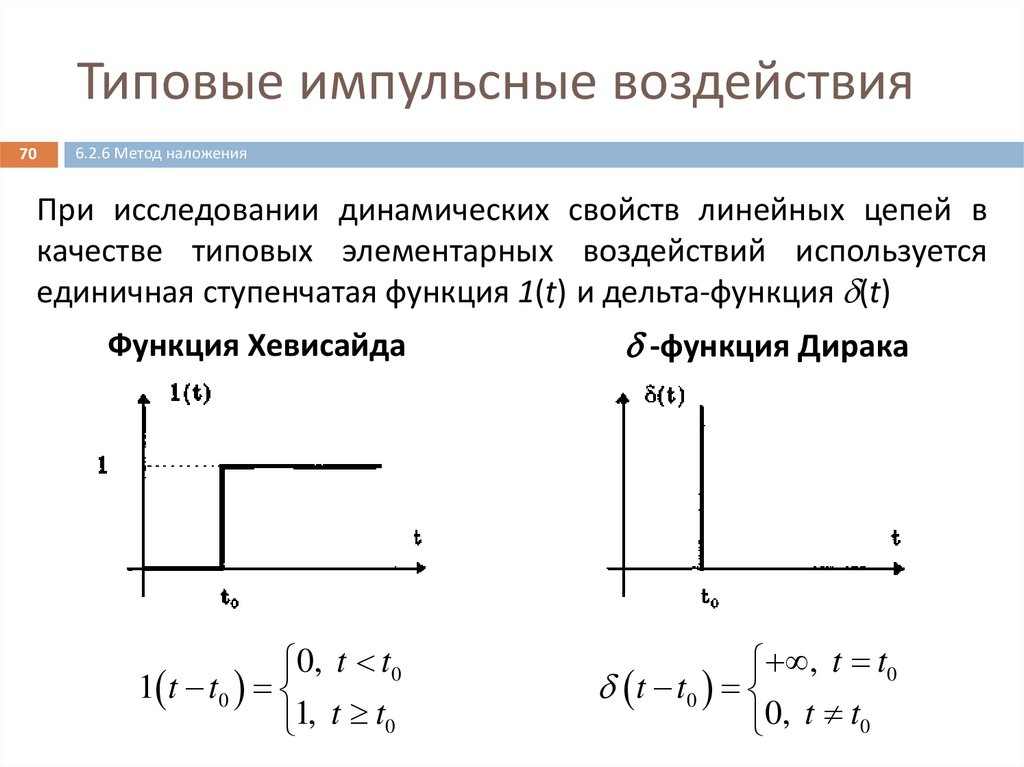
Типовые импульсные воздействия
70
6.2.6 Метод наложения
При исследовании динамических свойств линейных цепей в
качестве типовых элементарных воздействий используется
единичная ступенчатая функция 1(t) и дельта-функция (t)
Функция Хевисайда
-функция Дирака
0, t t0
1 t t0
1, t t0
, t t0
t t0
0, t t0

71.

Свойства и применение 1(t)
71
6.2.6 Метод наложения
• Коммутация электрических цепей
0, t t0
f t 1 t t0
f t , t t0
• Представление прямоугольного импульса
S1 x 1 t t1
S2 x 1 t t2
Sn x 1 t t1 1 t t2
• Преобразование Лапласа
pt0
e
L 1 t t0 1 t t0 e pt dt e pt dt
p
0
t0

72.

Переходная характеристика
6.2.6 Метод наложения
72
Переходной характеристикой h1(t-t0) линейной цепи, не
содержащей независимых источников энергии, называется
отношение реакции этой цепи на воздействие неединичного
скачка тока или напряжения к высоте этого сигнала при
нулевых начальных условиях
x t x 1 t t0 воздействие в виде неединичного скачка
y t реакция цепи
h t t0
1
y t
x
При x 1 h1 t t0 y t
Переходная характеристика цепи численно равна реакции цепи
на воздействие единичного скачка тока или напряжения

73.

Переходная характеристика
73
6.2.6 Метод наложения
pt0
xe
p
x t x 1 t t0
X p
воздействие на цепь
y t Y p реакция цепи
Y p
H p
X p
h1 t t0
операторная характеристика цепи
Y p H p X p H p xe pt0 H p e pt0
p
xp
x
x
При t0 0 h t
1
H p
p

74.

Порядок нахождения h1(t)
74
6.2.6 Метод наложения
1. Составление операторной схемы замещения цепи
для нулевых начальных условий
2. Нахождение операторной характеристики H(p)
3. Определение переходной характеристики
H p
1
h t
p

75.

75
Пример 1
RC-цепь с емкостью на выходе
6.2.6 Метод наложения
x t U1 t воздействие на цепь
y t U 2 t реакция цепи
1. Составление операторной схемы замещения цепи
для нулевых начальных условий

76.

76
Пример 1 (продолжение)
RC-цепь с емкостью на выходе
6.2.6 Метод наложения
2. Нахождение операторного коэффициента передачи по
напряжению
U2 p
1 pC
1
H p KU p
U1 p R 1 pC RCp 1
3. Определение переходной характеристики
h t
1
H p
p
1
p RCp 1
t
h t 1 exp
RC постоянная
времени цепи
1

77.

77
Пример 2
RC-цепь с сопротивление на выходе
6.2.6 Метод наложения
x t U1 t воздействие на цепь
y t U 2 t реакция цепи
1. Составление операторной схемы замещения цепи
для нулевых начальных условий

78.

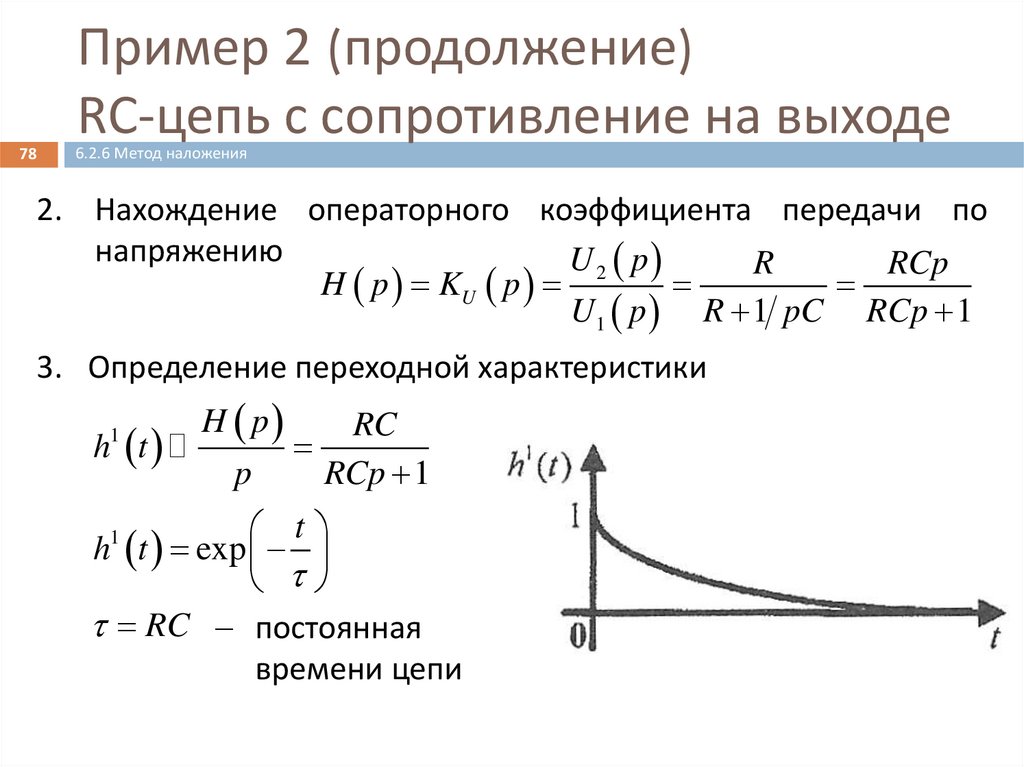
78
Пример 2 (продолжение)
RC-цепь с сопротивление на выходе
6.2.6 Метод наложения
2. Нахождение операторного коэффициента передачи по
напряжению
U2 p
R
RCp
H p KU p
U1 p R 1 pC RCp 1
3. Определение переходной характеристики
h t
1
H p
p
RC
RCp 1
t
h t exp
RC постоянная
времени цепи
1

79.

Интеграл Дюамеля
79
6.2.6 Метод наложения
Интеграл Дюамеля — метод расчета отклика линейных
пассивных систем на произвольно меняющийся во времени
входной сигнал.
Основан на принципе суперпозиции.
Отклик линейной пассивной системы на составной сигнал,
равный сумме нескольких сигналов, представляет собой сумму
откликов от каждого из слагаемых сигналов.
h1 t переходная характеристика
x t воздействие, x t 0 при t t0
x t x t0 1 t t0 x k 1 t k
k
x k
dx
dt t k

80.

Интеграл Дюамеля (продолжение)
80
6.2.6 Метод наложения
По принципу суперпозиции:
dx
y t x t0 h t t0
h1 t k
dt t k
k
1
При 0
dx 1
y t x t0 h t t 0
h t d интеграл Дюамеля
d
t0
t
1
Отклик системы выражается в виде интеграла от произведения
задержанной переходной характеристики на входное
воздействие (свертка функций), который носит название
интеграла Дюамеля

81.

Импульсная характеристика
81
6.2.6 Метод наложения
Импульсной характеристикой цепи называют
реакцию цепи на воздействие единичной импульсной
функции ( -функции)
1
dh
t
1
h t h 0 t
dt
t
t
0
0
h1 t h t dt h1 0 h t dt

82.

Контрольная работа № 1
82
Вариант 1
Вариант 2
1. Найти эквивалентное сопротивление между узлами A и D , а также
определить ток I для следующей цепи
Ri 1 кОм
Ri 2 кОм
U AD 5 В
U AD 10 В
2. Определить значения токов для всех ветвей цепи. Расчет произвести
методами контурных токов и узловых напряжений.
R1 R2 1 кОм
R1 R2 3 кОм
R3 3 кОм
R3 1 кОм
E1 5 В, E2 12 В
E1 12 В, E2 5 В

83.

Контрольная работа № 2
83
Вариант 1
1.
Записать
в
показательной
и
тригонометрической форме комплексные
амплитуды напряжения и тока. Определить
угол сдвига фаз между напряжением и
током, комплексное сопротивление и
проводимость цепи; активную, реактивную,
полную и комплексную мощности.
U 3 j4 B
2.
Вариант 2
1.
I 5 j A
К последовательной RL-цепи подключен
гармонический источник ЭДС
Записать
в
показательной
и
тригонометрической форме комплексные
амплитуды напряжения и тока. Определить
угол сдвига фаз между напряжением и
током, комплексное сопротивление и
проводимость цепи; активную, реактивную,
полную и комплексную мощности.
U 3 j4 B
2.
I 2 j7 A
К последовательной RC-цепи подключен
гармонический источник ЭДС
u t 220 2 sin 100 t .
u t 220 2 sin 100 t .
Определить R и L если действующее
значение тока в цепи I = 2.2 А, а сдвиг фаз
между напряжением и током равен 45 .
Построить
векторную
диаграмму
напряжений и тока. Чему равны активная,
реактивная и полная мощности цепи?
Определить R и С если действующее
значение тока в цепи I = 2.2 А, а сдвиг фаз
между напряжением и током равен 45 .
Построить
векторную
диаграмму
напряжений и тока. Чему равны активная,
реактивная и полная мощности цепи?