469.18K

Категория: $Математика$ Математика

Похожие презентации:

Решение нелинейных уравнений

Численное решение нелинейных уравнений

Решение нелинейных уравнений

Приближенное решение нелинейных уравнений

Решение нелинейных уравнений

Решение нелинейного уравнения. Тема 6

Решение нелинейных уравнений

2.

Методы решения
нелинейных уравнений
Метод половинного деления
Метод хорд
Метод касательных
Метод секущих
Метод простой итерации

Метод половинного
деления (дихотомии)
1.
В качестве первого приближения берем
x1
2.
3.
4.
a b
2
Если f(x1)=0, то это корень, иначе переход
к п.3.
Из двух половинок отрезка выбираем ту,
на концах которой функция имеет разные
знаки (роль a или b играет точка x1).
Если a b , то переход к п. 2., иначе
закончить вычисления.

4.

y
f (b)
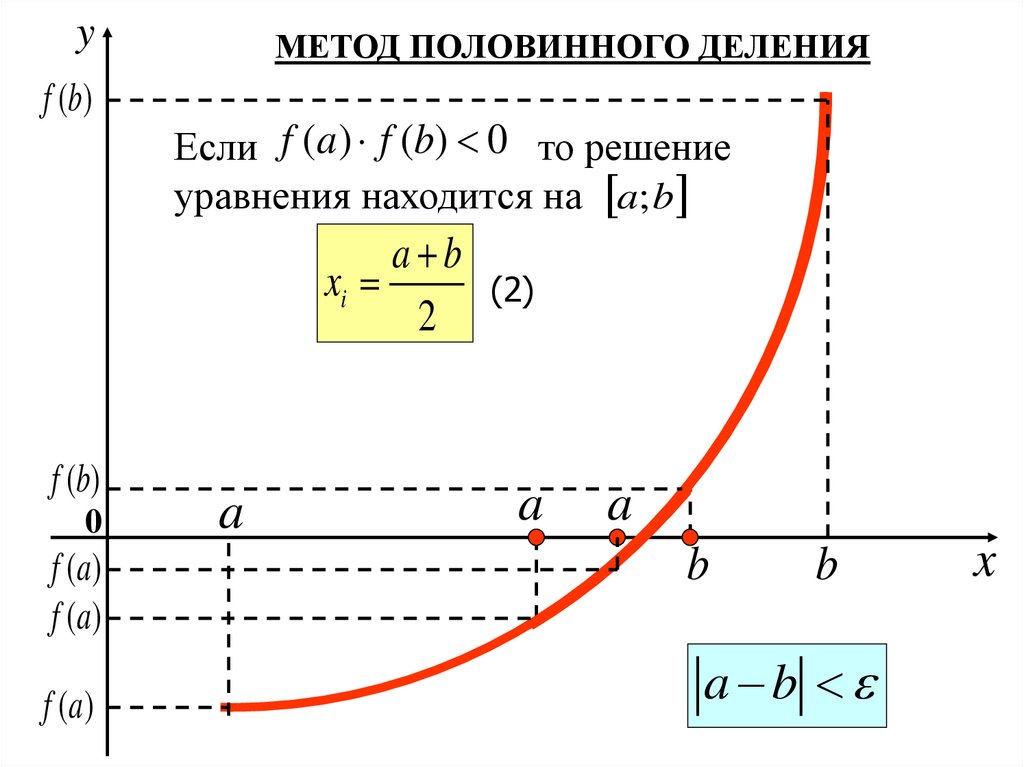
МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
Если f (a) f (b) 0 то решение
уравнения находится на a; b
a b
xi
(2)
2
f (b)
0
f (a)
f (a)
f (a)
a
a
a
b
b
a b
x

5.

Погрешность
половинного деления
На каждом шаге погрешность
гарантированно уменьшается ровно
вдвое. За n делений отрезок
уменьшается в 2n раз. Например, при
начальной длине отрезка 1, за 5
делений он уменьшается в 32 раза:
1 1
0,016
2 32

6.

Можно априорно рассчитать по заданной
погрешности количество шагов N(ε),
необходимых для достижения точности ε:
b a
,
n
2
b a
ln
b a
N
1, 4427 ln
1
ln 2
Например, для отрезка длиной 1 и =0,001
N 9,96... 1 10.

7.

Скорость сходимости
метода половинного
деления
В данном методе выполняется
условие:
|x*-xi+1|≤ q |x*-xi| при q=½,
т.е. имеет место линейная
сходимость.

8.

Особенности метода
половинного деления
Самый алгоритмически простой и надежный
метод.
Гарантированно сходится и скорость
приближения не зависит от гладкости
функции.
Обеспечивает двустороннее приближение к
корню.
Для увеличения точности приходится резко
увеличивать объем вычислений в силу
малой скорости сходимости.

9.

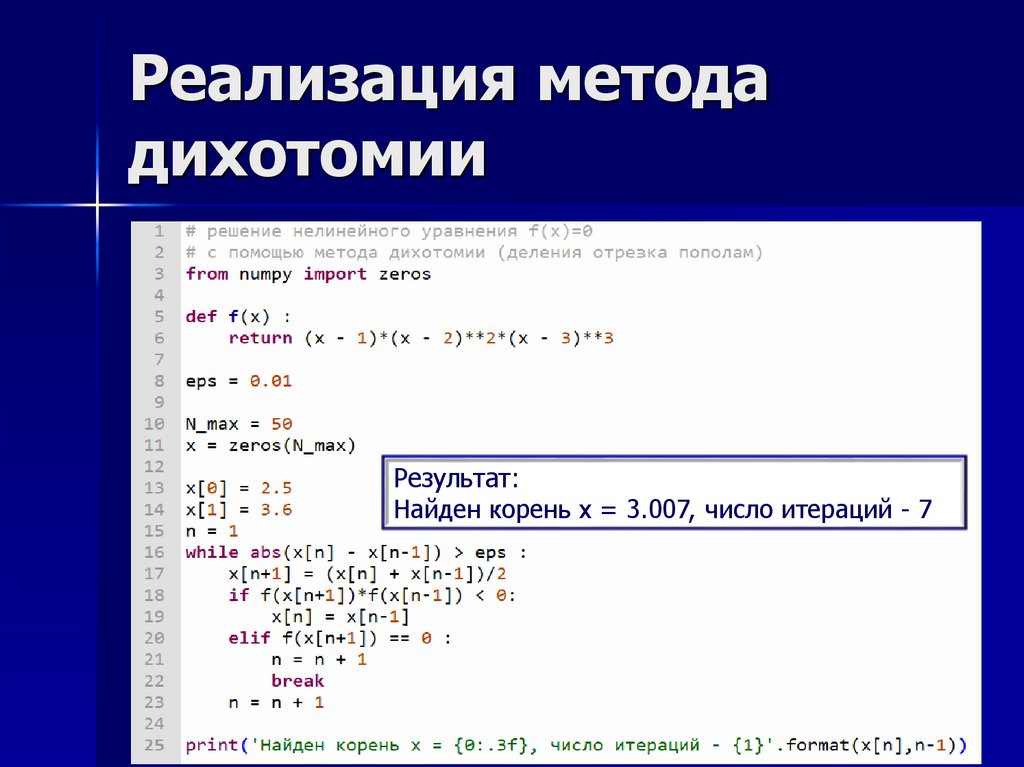
Реализация метода
дихотомии
Результат:
Найден корень x = 3.007, число итераций - 7

10.

Метод хорд
Идея метода основана на том, чтобы
использовать не только разность знаков
функции на концах отрезка, но и сами
значения в этих точках для построения
очередного приближения к корню.
Очередным приближением выбирается не
середина отрезка [a;b], а точка
пересечение с осью ОХ отрезка,
проходящего через точки (a, f(a)) и
(b,f(b)).

11.

МЕТОД ХОРД
y
Уравнение хорды:
f ( xi )
xi 1 xi
(b xi ) (3)
f (b) f ( xi )
x0=а
0
x1
x2
x3
x4
b
a x0 x1 ... xi xi 1 ... x* b
x

12.

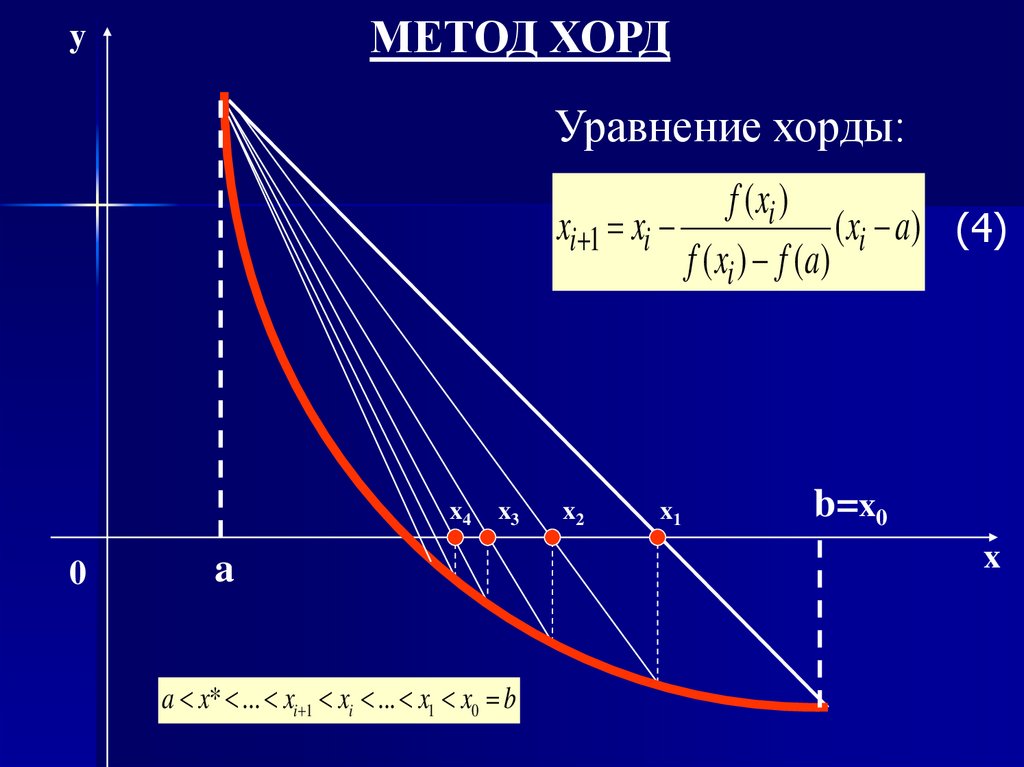
МЕТОД ХОРД
y
Уравнение хорды:
f ( xi )
xi 1 xi
( xi a) (4)
f ( xi ) f (a)
x4
0
x3
a
a x* ... xi 1 xi ... x1 x0 b
x2
x1
b=x0
x

13.

Формулы метода хорд
b xi
xi 1 xi f ( xi )
(3) f ( xi ) f (b) 0
f (b) f ( xi )
двигается левый конец интервала
xi a
xi 1 xi f ( xi )
(4) f ( xi ) f (a) 0
f ( xi ) f (a )
двигается правый конец интервала

14.

Оценка погрешности
b xi
xi 1 xi f ( xi )
f (b) f ( xi )
f (b) f ( xi )
f ( xi )
( xi xi 1 )
b xi
f ( i )( xi xi 1 ).

15.

Оценка погрешности
Теорема Лагранжа. Пусть функция f
определена на некотором
промежутке и имеет на нем
конечную производную f’. Если две
точки x и x0 находятся в данном
промежутке, то существует точка ξ
между x и x0 такая, что
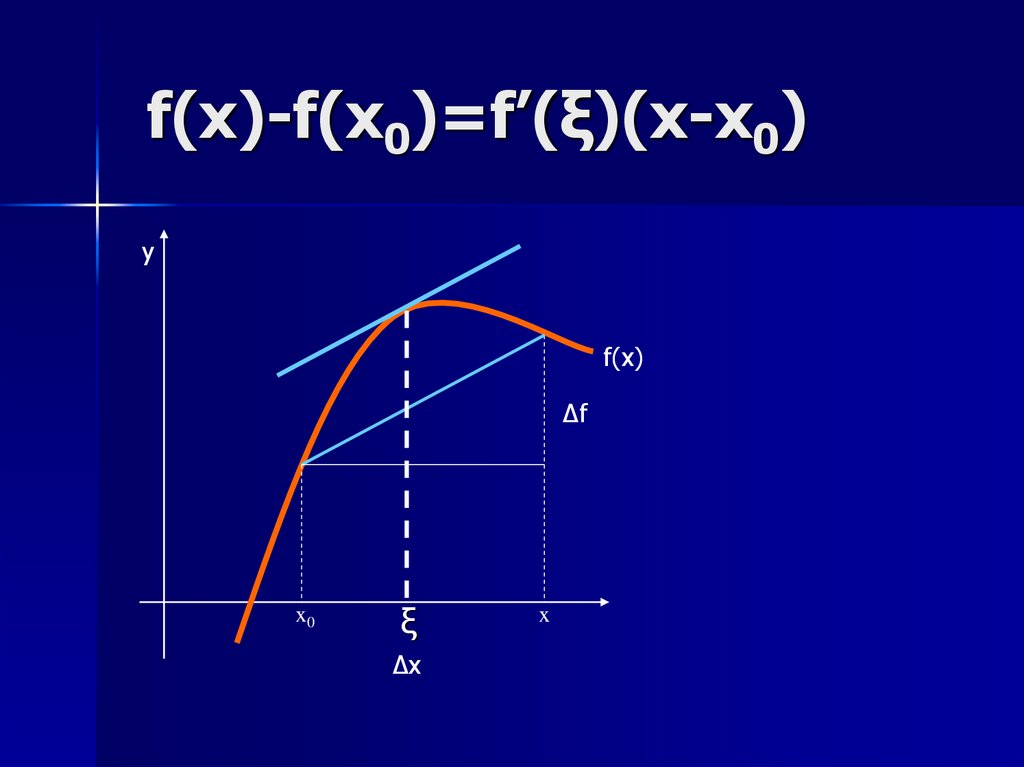
f(x)-f(x0)=f’(ξ)(x-x0)

16.

f(x)-f(x0)=f’(ξ)(x-x0)
y
f(x)
Δf
x0
ξ
∆x
x

17.

Погрешность метода
хорд
Если f’ и f’’ непрерывны, а числа m и M
такие, что
0 m f ( x) M , x a; b
тогда погрешность оценивается формулой
M m
xi xi 1 , i 1, 2,....
m
(5)

18.

Достижение точности
Для условия достижения заданной точности можно
воспользоваться оценкой (5):
m
M m
Однако, если интервал [a, b] небольшой, то
xi xi 1
можно предположить, что
M 2 m
Тогда для условия достижения заданной точности
можно воспользоваться соотношением:
x * xi xi xi 1

19.

Особенности метода
хорд
Обычно сходиться быстрее, чем
метод половинного деления.
Не зависит от вида конкретной
функции, хотя она должна быть
дифференцируема.
Имеет линейную скорость
сходимости.
Обладает односторонней
сходимостью.

20.

Метод касательных
(метод Ньютона)
Основная идея состоит в построении
очередного приближения не хордой,
а касательной к графику функции
y=f(x) в точке (xi, f(xi)).
Выбор начального приближения x0
зависит от вида графика функции на
данном отрезке.

21.

Метод касательных.
y
B0
Уравнение касательной:
y f ( xi ) f ( xi )( x xi )
B1
xi 1 xi
f ( xi )
(6)
f ( xi )
B2
a
0
B3
x3
x2
x1 b x
0
f ( xi )
x

22.

Анализ сходимости метода
Ньютона
Формула Тейлора с остаточным
членом в форме Лагранжа
f ( x0 )
f ( x) f ( x0 ) f ( x0 )( x x0 )
( x x0 ) 2 ...
2!
( n 1)
f ( n ) ( x0 )
f
(c )
n
( x x0 )
( x x0 ) n 1
n!
(n 1)!

23.

Пусть x* - точный корень из [a;b], xn ≈ x*.
Тогда между xn и x* найдётся точка ξn
такая, что
1
f ( x*) f ( xn ) f ( xn )( x * xn ) f ( n )( x * xn ) 2
2
Если xn достаточно близко к x*, то можно
отбросить третье слагаемое и получить
приближенное равенство:
f ( x*) 0 f ( xn ) f ( xn )( x * xn )
Отсюда
x* xn f ( xn ) f ( xn )
xn 1 xn f ( xn ) f ( xn )

24.

Оценка погрешности
метода касательных
Если f ( x ) m, f ( x ) M 2 , то
M2
2
x
( xn xn 1 ) (7)
2m
Фактически в окрестности корня на каждой
итерации погрешность возводиться в квадрат, т.е.
число верных знаков удваивается. Но в эту
окрестность еще надо попасть. Если область
сходимости мала, то метод чувствителен к
начальному приближению.

25.

Достижение точности
Для условия достижения заданной точности
и прекращения вычислений можно
использовать оценку (7):
2m
( xn xn 1 )
M2
2

26.

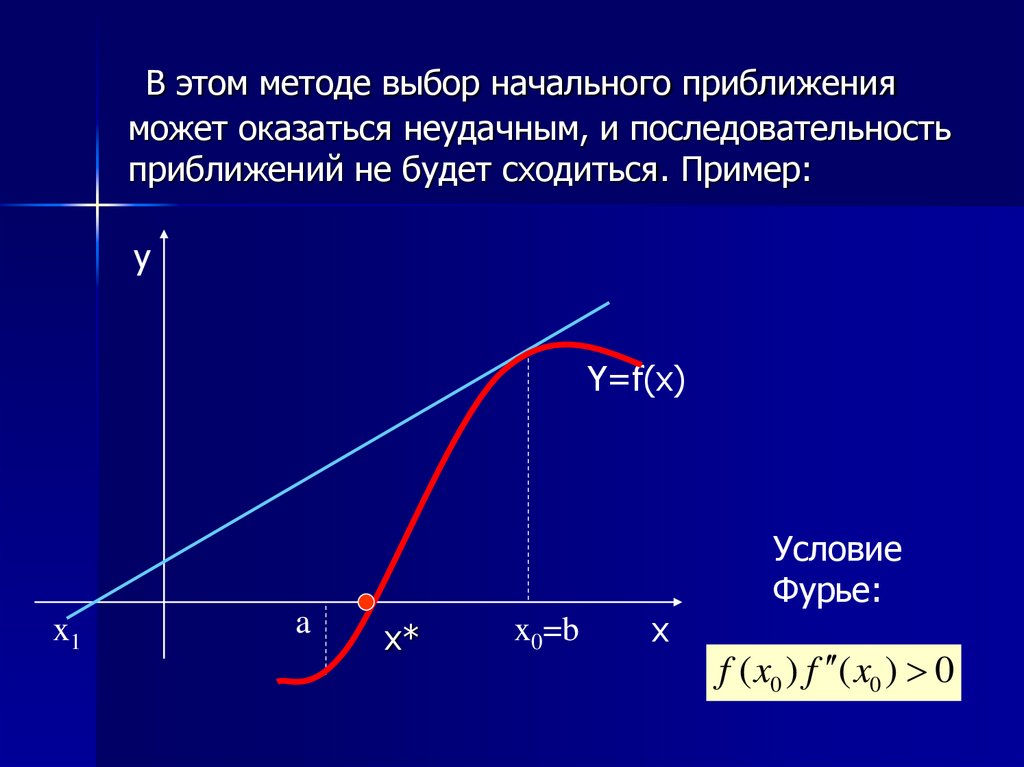
В этом методе выбор начального приближения
может оказаться неудачным, и последовательность
приближений не будет сходиться. Пример:
y
Y=f(x)
x1
a
x*
x0=b
x
Условие
Фурье:
f ( x0 ) f ( x0 ) 0

27.

Особенности метода
касательных
Наиболее быстро сходящийся метод
(квадратичная скорость
сходимости).
Необходимо вычислять в каждой
точке приближения производную.
Сходимость метода односторонняя.
Требует хорошего начального
приближения в случае малой
области сходимости.

28.

Недостатки метода Ньютона можно
преодолеть следующим образом:
Для выхода в непосредственную близость
корня сначала применяют
гарантированный медленный метод, а
затем переходят на метод Ньютона.
Затруднение с вычислением производной
можно избежать, заменив ее конечноразностным отношением:
f ( xi ) f ( x i 1 )
f
f ( xi )
x
xi xi 1

29.

Исторический пример
использования метода
Эмпирически метод касательных
применялся в древности для нахождения
квадратного корня (длины гипотенузы).
Пусть f(x)=x2 - a,
тогда решением уравнения f(x)=0
является:
a

30.

Пример
Составим рекуррентное соотношение:
f ( xi )
xi 1 xi
f ( xi )
xi a 1
a
xi 1 xi
( xi )
2 xi
2
xi
2

31.

Пример: a=9
1
a
xi 1 ( xi )
2
xi
x0 9
1
9
x1 (9 ) 5
2
9
1
9
x2 (5 ) 3.4
2
5
1
9
x3 (3.4
) 3.023529...
2
3.4
1
9
x4 (3.023529
) 3.000091...
2
3.023529
1
9
x5 (3.000091
) 3.000000...
2
3.000091

32.

Метод секущих
– это упрощение метода касательных, когда
затруднительно найти производную.
Заменим в методе касательных
производную конечно-разностным
отношением:
f (x ) f (x )
f ' ( xi )
xi 1 xi
i
i 1
xi xi 1
xi xi 1
f ( xi ) (8)
f ( xi ) f ( xi 1 )

33.

Особенности метода
секущих
Не требует дифференцированной
функции.
При его реализации на каждой итерации
вычисляется только одно новое значение
функции.
Требует два начальных приближения x0 и
x1. Обычно это один из концов отрезка и
близкая к нему точка.
Метод уступает в скорости сходимости
методу касательных (сверхлинейная
скорость с α=1.618).

34.

Метод простой итерации
Рассмотренные методы решения
уравнения f(x)=0 сводились к
итерационной процедуре вида
xi+1=φ(xi) (9)
Основная идея метода простой
итерации состоит в том, чтобы
построить универсальный метод
типа (9).

35.

Исходное уравнение f(x)=0 заменяют
эквивалентным ему x=φ(x).
После этого выбирается начальное
приближение x0, которое
подставляют в функцию φ(x):
x1= φ(x0)
x2= φ(x1)
……………
xi+1= φ(xi)
……………

36.

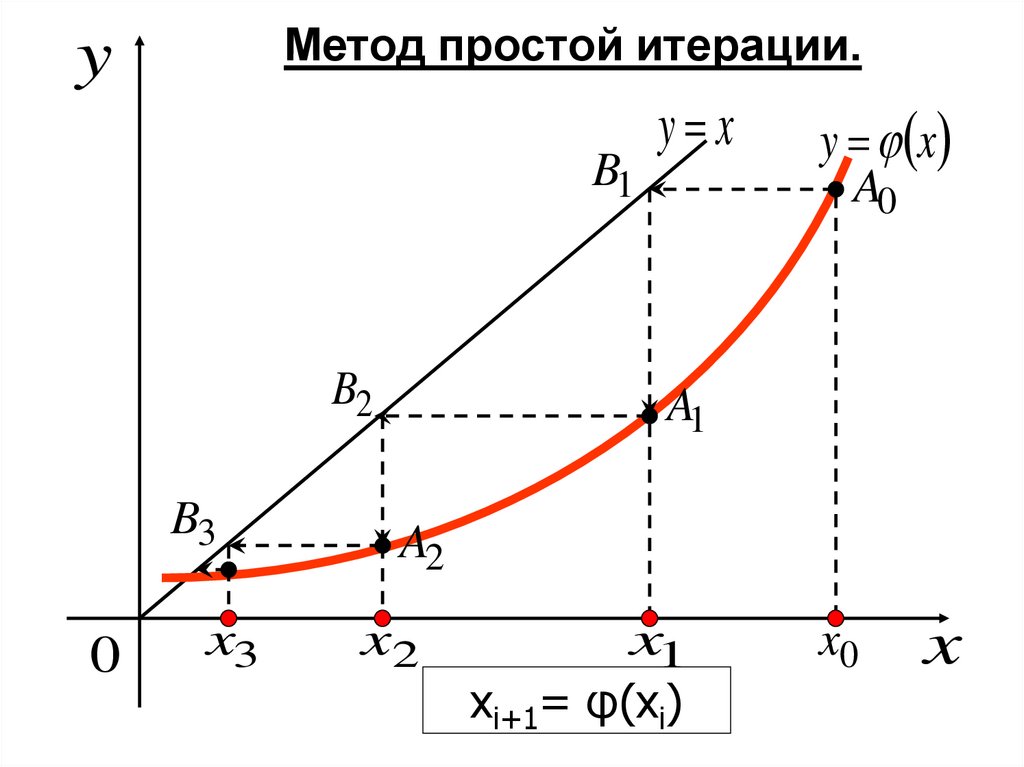
Метод простой итерации.
y
B1
B2
B3
0
x3
y x
y x
A0
A1
A2
x2
x1
xi+1= φ(xi)
x0
x

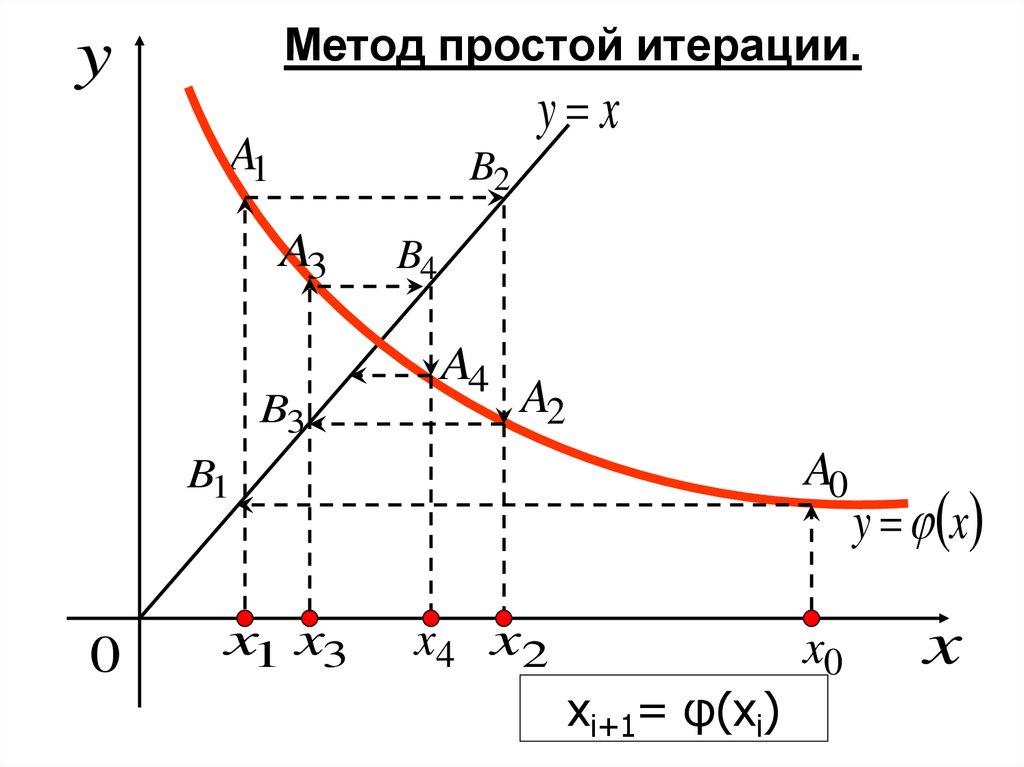
37.

Метод простой итерации.
y
y x
A1
B2
A3
B3
B4
A4
A2
B1
0
x1 x3
x4 x 2
xi+1= φ(xi)
A0
y x
x0
x

38.

Таким образом, получим
последовательность x0 ,x1 , x2 ,… , xi ,…
Рассмотрим, в каком случае она сходится.
Лагранжа
xi 1 x* ( x i ) ( x* )
( xi x* ) ' ( ) ' ( ) ( xi x* )
xi x
Условие сходимости:
*
' ( ) 1
Модуль φ’(x) в некоторой окрестности
корня должен быть меньше 1, чтобы
итерационный процесс сходился со
скоростью геометрической
прогрессии.

39.

Приведение уравнения к
итерационному виду
Пример 1.
f(x)=0
x=φ(x)
x tg ( x) 1 0
1
x arctg ( ) k
x

40.

Приведение уравнения к
итерационному виду
Пример 2.
x 3x 1 0
1
x=φ(x) x 2 3
x
f(x)=0
3
2

41.

Приведение уравнения к
итерационному виду
Способы приведения уравнения могут
быть различными, но важно добиться
выполнения условия сходимости:
' ( ) 1
в окрестности корня или на всем отрезке
[a;b]. Рассмотрим универсальный
способ приведения уравнения к
итерационному виду.

42.

В общем случае используется
следующий алгоритм:
f(x)=0 умножим на константу λ
• λ*f(x)=0 вычтем обе части из х
• x - λ*f(x) = x
• т.о., φ(x)= x- λ*f(x)
• подберем λ т. о., чтобы на [a,b]
выполнялось условие сходимости:
' 1

43.

Пример.
Пусть
f(x)=x3-x2-1000=0.
2
2
1
,
280 341 621 300
Итерационный вид уравнения:
Это ур-е имеет один
корень на [10,11].
x 3 x 2 1000
x x
.
300
Производная
f’(x)=3x2-2x на [10,11] x =10,
0
монотонно возрастает:
m1= f’(10)=280
M1= f’(11)=341.
x1=10.3333333,
x3=10.3446913,
x4=10.3446910.

44.

Подбор параметра λ
Пусть на отрезке [a;b] производная
функции f(x) ограничена:
0 < m1 ≤ f’(x) ≤ M1.
Положим λ=2/(M1+ m1).
Тогда
2m1
2
'( x) 1
f '( x) 1
M 1 m1
M 1 m1
M 1 m1
1.
M 1 m1

45.

Упражнение. На отрезке [1;2] привести к
итерационному виду уравнение
x4-2x-3=0.
Производная
f’(x)=4x3-2 на [1;2]
монотонно
возрастает:
m1= f’(1)=2
M1= f’(2)=30.
λ=2/(M1+ m1)
λ=2/(30+ 2)=1/16
φ(x)= x- λ*f(x)
x = x – (x4-2x-3)/16
3
’ = 1 – (2x3-1)/8
2
1
f(x)
0
0
-1
-2
-3
0,5
1
1,5
2
2,5
3
fi'(x)