Похожие презентации:
Неопределенный интеграл
1. Неопределенный интеграл
Лекция 13.10.2016 г.2. Элементы интегрального исчисления
1.Первообразная и неопределенный интеграл2.Основные приемы вычисления
неопределенных интегралов
3.Интегрирование функций, содержащих
квадратный трехчлен
4.Интегрирование дробно-рациональных
функций
5.Интегрирование тригонометрических
функций
6.Интегрирование некоторых
иррациональностей
3. Неопределенный интеграл, его свойства и вычисление
4. Первообразная и неопределенный интеграл
Определение. Функция F x называетсяпервообразной функции f x , определенной на
некотором промежутке, если F x f x для
каждого x из этого промежутка.
Например, функция cos x является
первообразной функции sin x , так как
cos x sin x .
5. Первообразная и неопределенный интеграл
Если F x - первообразная функции f x ,то F x C , где C - некоторая постоянная,
также является первообразной функции
f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.
6. Первообразная и неопределенный интеграл
Определение. Совокупность всехпервообразных функции f x ,
определенных на некотором
промежутке, называется
неопределенным интегралом от
функции f x на этом промежутке и
обозначается f x dx .
7. Первообразная и неопределенный интеграл
Если F x - некоторая первообразная функцииf x , то пишут f x dx F x C , хотя
правильнее бы писать f x dx F x C .
Мы по устоявшейся традиции будем писать
f x dx F x C .
Тем самым один и тот же символ
f x dx будет обозначать как всю
совокупность первообразных функции f x ,
так и любой элемент этого множества.
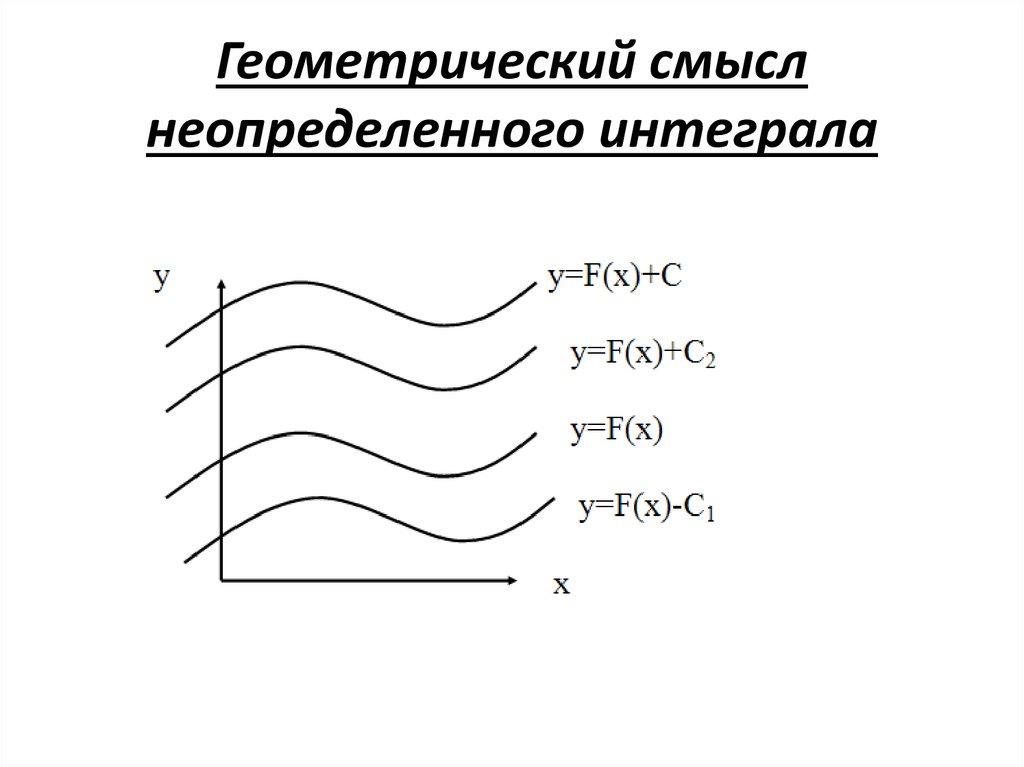
8. Геометрический смысл неопределенного интеграла
9. Свойства интеграла, вытекающие из определения
Производная неопределенного интеграларавна подынтегральной функции, а его
дифференциал- подынтегральному
выражению. Действительно:
1. ( f ( x)dx) ( F ( x) C ) F ( x) f ( x);
2. d f ( x)dx ( f ( x)dx) dx f ( x)dx.
10. Свойства интеграла, вытекающие из определения
Неопределенный интеграл от дифференциаланепрерывно дифференцируемой функции равен
самой этой функции с точностью до постоянной:
3. dF ( x) F ( x)dx F ( x) C ,
так как F (x) является первообразной для F (x).
11. Свойства интеграла
4. Если функции f1 x и f 2 x имеютпервообразные, то функция f1 x f 2 x
также имеет первообразную, причем
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx K f x dx ;
6. f x dx f x C ;
7. f x x dx F x C .
12. Таблица неопределенных интегралов
1. dx x C .a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
13. Таблица неопределенных интегралов
11.dx
arcsin x C .
1 x
dx
1
x
13. 2 2 arctg C .
a
a
a x
15.
12.
2
dx
1
x a
ln
C
2
2
2a x a
x a
14.
16.
dx
arcsin
x
C ..
a
a2 x2
dx
ln x x 2 a C .
x2 a
dx
1
a x
ln
a 2 x 2 2a a x C .
14. Использование свойств дифференциала
При интегрировании удобно пользоватьсясвойствами:
1
1. dx d (ax)
a
1
2. dx d (ax b),
a
1 2
3. xdx dx ,
2
1 3
2
4. x dx dx .
3
15. Примеры
Пример . Вычислить cos 5xdx .Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5
16. Примеры
Пример. Вычислить x 3x x 1 dx .Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
x
2
2
3
3 x 3 x 1 dx x 2 dx 3 x 3 dx xdx dx .
x4 x2
x3
3 x C
2
4
3
17. Интеграл от сложной функции, аргумент которой является линейной функцией
При вычислении интегралов удобно пользоватьсяследующими свойствами интегралов:
Если f x dx F x C , то f x b dx F x b C .
Если f x dx F x C , то f ax b dx F ax b C .
a
1
18. Пример
16
(2 3x) dx 3 6 (2 3x) C.
5
19. Методы интегрирования
20. Непосредственное интегрирование
Используя свойства неопределенного интеграла иформулы школьного курса, приводят
подынтегральную функцию к табличному виду.
21. Замена переменной
Требуется найти f x dx , причемнепосредственно подобрать первообразную
для f x мы не можем. Часто удается найти
первообразную, введя новую переменную,
по формуле
f x dx f t (t )dt , где x t , а t t
новая переменная.
Подынтегральное выражение представляет
собой дифференциал сложной функции.
Предположить вид новой переменной
поможет знание таблицы производных.
22. Интегрирование по частям
.Этот метод основан на формуле udv uv vdu
Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
в) x n arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
При вычислении интегралов а) и б) вводят
n 1
обозначения: x n u , тогда du nx dx , а, например
sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию
arctgx , ln x , а за dv берут x n dx .
23. Вспомогательная таблица для интегрирования по частям
24. Примеры
Пример. Вычислить x cos xdx .Решение.
u x, du dx
xcosxdx
dv cosxdx, v cosxdx
=
= x sin x sin xdx x sin x cos x C .
25.
Пример. Вычислитьdx
u ln x, du x x 2
x 2 dx
=
ln x
x
ln
xdx
2
2 x
x
2
dv xdx, v 2
x2
1
x2
1 x2
=
ln x xdx
ln x
C .
2
2
2
2 2
























 Математика
Математика








