Уравнения пространственного движения самолета (лекция 5)

1.

Дисциплина: Системы автоматического управления полетом
РАЗДЕЛ 1. ВОЗДУШНОЕ СУДНО КАК ОБЪЕКТ УПРАВЛЕНИЯ.
Тема 1. Основные положения динамики управления полетом
ЛЕКЦИЯ № 5 УРАВНЕНИЯ ПРОСТРАНСТВЕННОГО
ДВИЖЕНИЯ САМОЛЕТА
Учебные вопросы:
1 Кинематические уравнения движения самолета.
2 Нелинейная модель пространственного движения самолета.
3 Разделение пространственного движения самолета на продольное и
боковое.
Задание на самостоятельную работу:
[1] Вавилов Ю.А. Системы автоматического управления полетом. ВВИА им. проф. Н.Е.
Жуковского и Ю.А Гагарина, 2009. с. 19…22, 24...32.
[2] Мигунов А.И., Иванов Р.В., Серов А.Н. Системы автоматического управления полетом.
Электронный учебник. ВУНЦ ВВС «ВВА», 2016. Л-5, тематический план, учебная программа
[3] Красовский А.А., Вавилов Ю.А., Сучков А.И. Системы автоматического управления
летательных аппаратов. ВВИА им. проф. Н.Е. Жуковского, 1986. с. 17…24.
[7] Кичигин Е.К., Демчук В.А., Лущик А. В., Агеев А.М. Системы автоматического
управления полетом. Ч. 1: Учебное пособие. -Воронеж: ВАИУ, 2011. с. 9…13.

2.

Вопрос №1
Кинематические уравнения движения
самолета

3.

На предыдущей лекции были получены нелинейные динамические
уравнения пространственного движения самолета как ТТ в связанной СК:
Vx 0
m Vy z
Vz y
z
0
x
y Vx Fx
x Vy Fy
0 Vz Fz
I x x y z I z I y M x ;
I y y x z I x I z M y ;
I z z x y I y I x M z .
В результате решения этих дифференциальных уравнений можно получить текущие
значения линейной земной скорости VK и угловой скорости движения ЛА в
проекциях на оси связанной СК.

4.

Кроме векторов управления и возмущения необходимо иметь значения углов Эйлера
ϑ, γ, ψ, атаки α, скольжения β, скорости (воздушной) V , высоты полета Н самолета, а
также, угол наклона траектории θ и путевой угол Ψ.
Они вычисляются по кинематическим уравнениям движения и уравнений связи.
Кинематическими
называют
уравнения,
которые
связывают
кинематические параметры движения тела ( V , ) с параметрами его
положения L,H ,Z , , ,
в данном случае нормальной земной СК
(инерциальной) 0o X gYg Z g .
Кинематические уравнения поступательного движения определяют положение
ЦМ ЛА в пространстве (в нормальной земной СК) и имеют вид:
Wx
Wx
X g L W Xg
T
Y
H
W
M
W
M
M
M
W
y ,
gc y
g Yg
W
W
Z g Z W
Zg
z
z
(1)

5.

В развернутом виде
cos cos
L
sin
H
Z
sin cos
sin sin
cos sin cos
cos cos
cos sin
sin sin cos
sin cos
cos sin sin Wx
cos sin Wy
cos cos
Wz
sin sin sin
(2)
Для определения угловых параметров движения Ψ, θ самолета относительно
Земли представим вектор земной скорости W , в проекциях на оси нормальной
СК OXgYgZg:
Wxg
Wx
W
cos cos
0 W sin
W
M
,
,
W
M
,
yg
gc
gk
y
W
W
0 k
cos sin g
zg
z c
g
Кинематические уравнения поступательного движения в векторноматричной форме
cos cos
T
М gk М М sin cos
sin
sin
cos
0
sin cos
sin sin
cos
T
cos
М sin
0
sin
cos
0
0
0 ;
1
cos
М 0
sin
0 sin
1
0
(3)
0 cos

6.

Для
определения
параметров
углового положения самолета - углов
ϑ, γ, ψ пространственной ориентации
самолета
(связанной
СК)
воспользуемся
следующими
соображениями.
Последовательно
поворачивая нормальную СК OXgYgZg
относительно OYg ,OZ*,OX
осей
соответственно на углы ϑ, γ, ψ ее
можно совместить со связанной СК
OXYZ
Yg
Y*
X
Y
X*
Xg
Z*
Zg
Рис. 1
Z
Очевидно, что угловые скорости , , , направленные вдоль осей OYg ,OZ*,OX ,
являются проекциями угловой скорости ЛА относительно нормальной СК.

7.

Yg
Проецируя это векторное выражение на оси связанной
СК, получим:
Y*
X
Y
x
0
0
М 0 М М 0 М М М ,
y
z
0
0
X*
Xg
Z*
Zg
0
1
М 0 cos
0 sin
0
cos sin 0
cos
sin ; М sin cos 0 ; М 0
0
sin
cos
0
1
Z
0 sin
1
0
0 cos
(4)
В результате имеем кинематические уравнения вращательного движения
самолета:
x sin
y sin cos cos
z cos sin cos

8.

Вопрос №2
Нелинейная модель пространственного
движения самолета

9.

Динамические уравнения поступательного движения
VKx 0
m VKy z
VKz y
z
0
x
y VKx
X a Px
0
x VKy M ca , Ya Py M cg , , G
0 VKz
Z a Pz
(5)
0
Динамические уравнения вращательного движения
I x x y z I z I y M x M Px ;
I y y x z I x I z M y M Py ;
I z z x y I y I x M z M Pz ,
(6)
Кинематические уравнения вращательного движения самолета
x sin
y sin cos cos
z cos sin cos
Кинематические уравнения поступательного движения
Wxg
Wx
W
cos cos
W
M
,
,
yg
gc
Wy M gk , 0 W sin
W
W
0 k
cos sin g
z c
zg
g
(7)

10.

Приведем эти уравнения к одной форме записи и получим нелинейную
математическую модель пространственного движения ВС в общем виде:
Динамические уравнения поступательного движения
VKx 0
m VKy z
VKz y
z
0
x
y VKx Fx
x VKy Fy
0 VKz Fz
m(VKx zVKy yVKz ) Fx
m(VKy xVKz zVKx ) Fy (9)
m(VKz yVKx xVKy ) Fz
(8)

11.

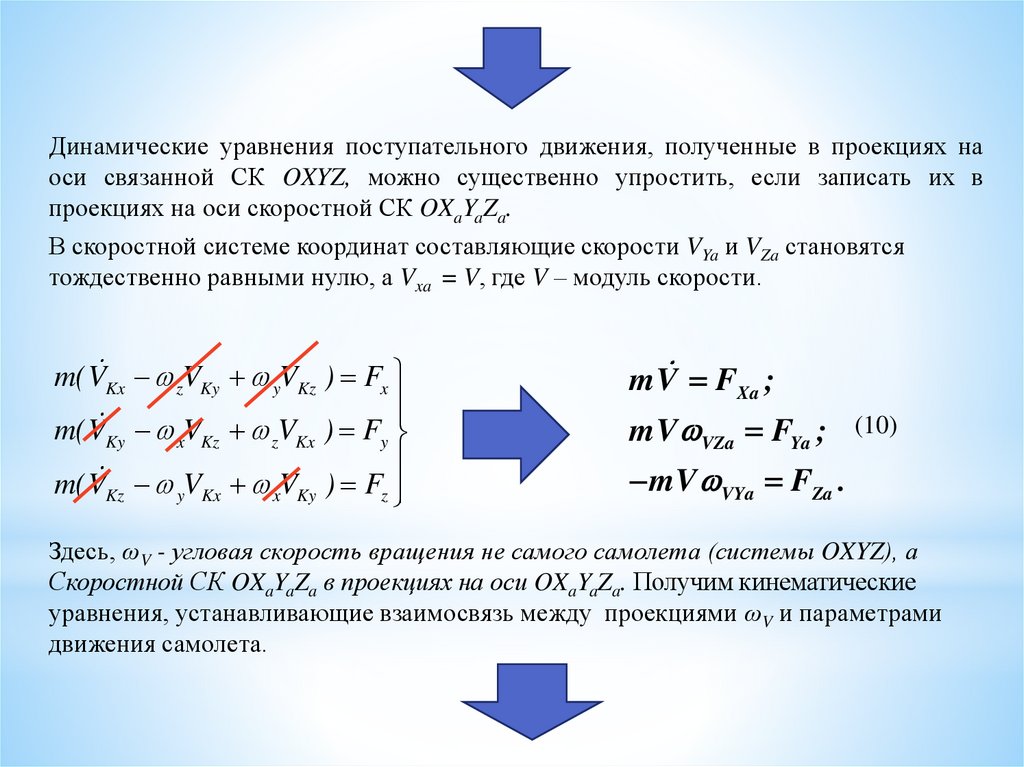
Динамические уравнения поступательного движения, полученные в проекциях на
оси связанной СК OXYZ, можно существенно упростить, если записать их в
проекциях на оси скоростной СК OXaYaZa.
В скоростной системе координат составляющие скорости VYa и VZa становятся
тождественно равными нулю, а Vxa = V, где V – модуль скорости.
m(VKx zVKy yVKz ) Fx
m(VKy xVKz zVKx ) Fy
m(VKz yVKx xVKy ) Fz
mV FXa ;
mV VZa FYa ;
(10)
mV VYa FZa .
Здесь, ωV - угловая скорость вращения не самого самолета (системы OXYZ), а
Скоростной СК OXaYaZa в проекциях на оси OXaYaZa. Получим кинематические
уравнения, устанавливающие взаимосвязь между проекциями ωV и параметрами
движения самолета.

12.

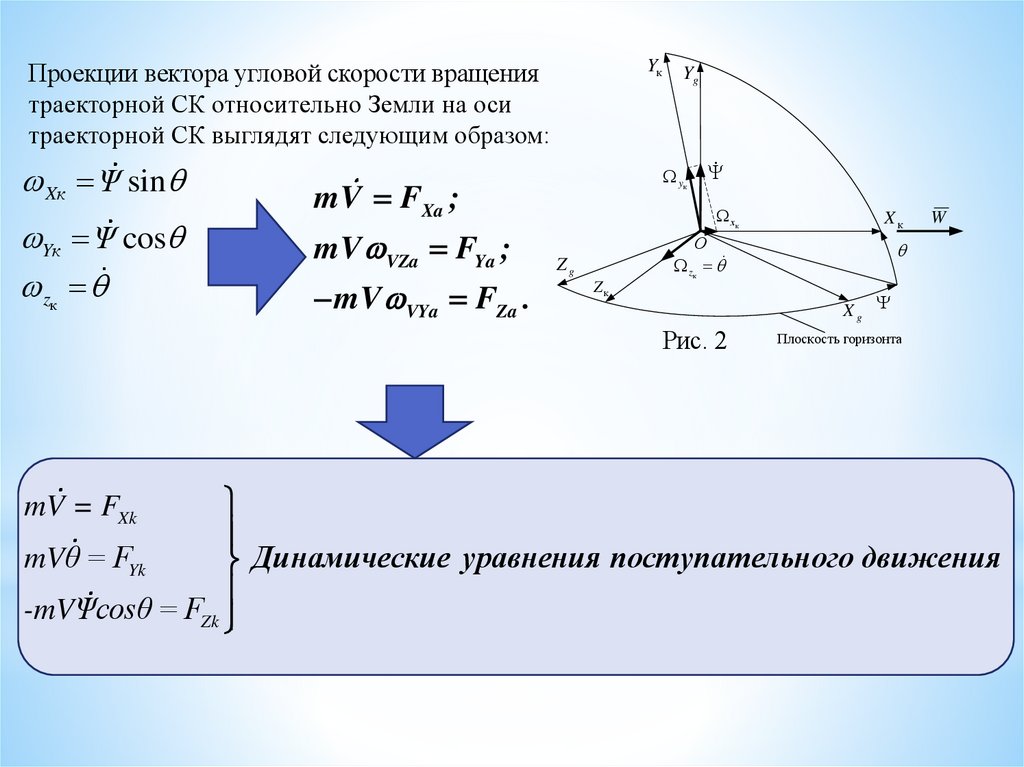
Проекции вектора угловой скорости вращения
траекторной СК относительно Земли на оси
траекторной СК выглядят следующим образом:
Xк Ψ sin
Yк Ψ cos
zк
Yк
yк
mV FXa ;
mV VZa FYa ;
mV VYa FZa .
Yg
хк
Xк
О
zк
Zg
Zк
W
Xg
Рис. 2
Плоскость горизонта
mVθ = FYk
Динамические уравнения поступательного движения
-mVΨcosθ = FZk
mV = FXk

13.

Динамические и кинематические уравнения вращательного движения, по-прежнему,
записываются в проекциях на оси Связанной СК OXYZ
I x x y z I z I y M x M Px
I y y x z I x I z M y M Py
I z z x y I y I x M z M Pz
x sin
y sin cos cos
z cos sin cos
Динамические уравнения вращательного
движения
(11)
Кинематические уравнения
вращательного движения самолета
(12)

14.

Кинематические уравнения поступательного движения
Wxg
Wx
W
cos cos
0 W sin
(13)
W
M
,
,
W
M
,
yg
gc
y
gk
W
W
0 k
cos sin g
zg
z c
g
Обозначим проекцию вектора Земной скорости на оси нормальной СК
W x , W y , W z , а сам вектор земной скорости W
xg
g
yg
g
zg
g
xg W cos cos
y g W sin
z g W cos sin

15.

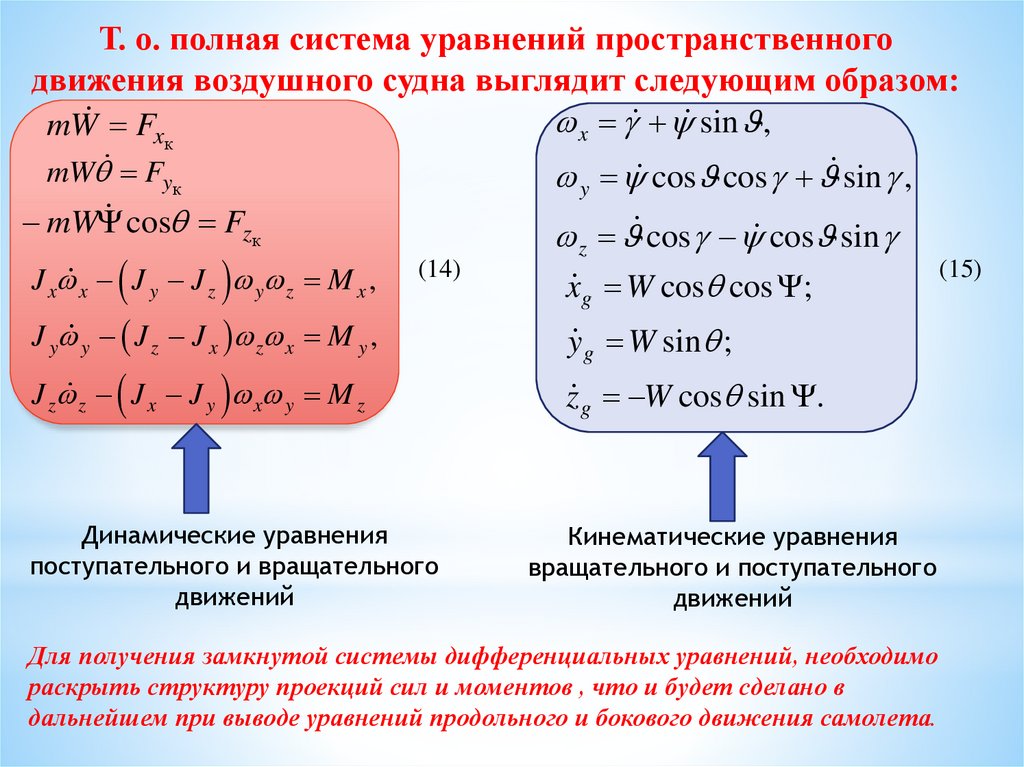
Т. о. полная система уравнений пространственного
движения воздушного судна выглядит следующим образом:
x sin ,
mW Fxк
mW Fyк
y cos cos sin ,
z cos cos sin
xg W cos cos ;
cos Fz
mW
к
J x x J y J z y z M x ,
(14)
J y y J z J x z x M y ,
J z z J x J y x y M z
Динамические уравнения
поступательного и вращательного
движений
y g W sin ;
z g W cos sin .
Кинематические уравнения
вращательного и поступательного
движений
Для получения замкнутой системы дифференциальных уравнений, необходимо
раскрыть структуру проекций сил и моментов , что и будет сделано в
дальнейшем при выводе уравнений продольного и бокового движения самолета.
(15)

16.

Вопрос №3
Разделение пространственного
движения самолета на продольное и
боковое.

17.

К ПРОДОЛЬНОМУ ДВИЖЕНИЮ САМОЛЕТА относят
движение центра масс в вертикальной плоскости и вращение относительно
поперечной связанной оси OZ (изменение угла тангажа).
Движение центра масс вдоль осей ОХ и ОУ и вращательное движение
относительно оси OZ.
К БОКОВОМУ – движение центра масс в плоскости горизонта и
угловые движения рыскания (вращение относительно OY) и крена
(вращение относительно OХ).
Движение центра масс вдоль оси OZ и вращательное движение
относительно осей ОХ и ОУ.
Рассмотрение
изолированных
движений
возможно
при
определенных условиях, поскольку в пространственном движении
значительную роль играют некоторые перекрестные связи –
аэродинамические, кинематические и инерционные, которые будут
рассмотрены в следующей лекции.

18.

Вопросы для подготовки
1.
Какие уравнения называются кинематическими?
2.
Чем обусловлена необходимость разделения пространственного
движения?
3.
Какое движение относят к продольному?
4.
Какое движение относят к боковому?
5.
Природа возникновения аэродинамических перекрестных связей?