Молекулярная физика

1.

Литература:
Трофимова Т.И. – Курс Физики
Савельев И.В. – Курс физики, том 1 – Механика и Молекулярная Физика
Савченко Н.Е. – Решение задач по физике
Фирганг Е.В. - Руководство к решению задач по курсу общей физике
1

2.

Молекулярная физика — раздел физики, в котором изучаются
строение и свойства вещества исходя из того, что все тела
состоят из молекул, находящихся в непрерывном хаотическом
движении.
Процессы, изучаемые молекулярной
физикой, являются результатом совокупного
действия огромного числа молекул
Термодинамика — раздел физики, в котором изучаются общие
свойства макроскопических систем, находящихся в состоянии
термодинамического равновесия, и процессы перехода между
этими состояниями. Термодинамика не рассматривает
микропроцессы, которые лежат в основе этих превращений.
2

3.

Молекулярно-кинетическая теория идеальных газов
модель идеального газа
1) собственный объем молекул
газа пренебрежимо мал по
сравнению с объемом сосуда;
2) между молекулами газа
отсутствуют силы
взаимодействия;
Эмпирические законы идеальных газов
Закон Бойля — Мариотта
Законы Гей-Люссака
1)
T = t+273.15
3) столкновения молекул газа
между собой и со стенками
сосуда абсолютно упругие.
2)
3

4.

Молекулярно-кинетическая теория идеальных газов
Эмпирические законы идеальных газов
Закон Авогадро:
1 моль любого газа при одинаковых температуре и давлении занимает
одинаковый объем.
При нормальных условиях этот объем равен 22.4·10-3 м3/моль
Закон Дальтона:
давление смеси идеальных газов p равно сумме парциальных давлений
р1, р2, ..., рn входящих в нее газов
Парциальное давление — давление, которое производил бы газ,
входящий в состав газовой смеси, если бы он один занимал объем,
равный объему смеси при той же температуре.
4

5.

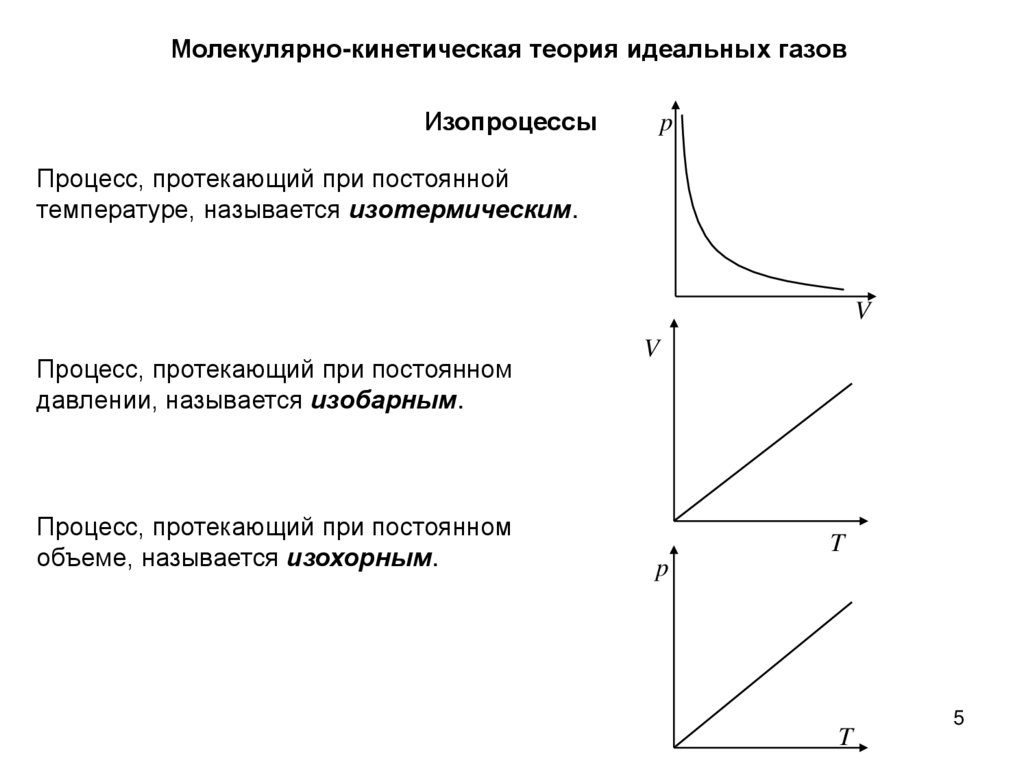
Молекулярно-кинетическая теория идеальных газов
Изопроцессы
p
Процесс, протекающий при постоянной
температуре, называется изотермическим.
V
Процесс, протекающий при постоянном
давлении, называется изобарным.
Процесс, протекающий при постоянном
объеме, называется изохорным.
V
T
p
T
5

6.

Молекулярно-кинетическая теория идеальных газов
Уравнение состояния идеального газа
Состояние некоторой массы газа определяется тремя термодинамическими
параметрами: давлением р, объемом V и температурой Т. Между этими
параметрами существует определенная связь, называемая
уравнением состояния
pV
m
RT RT - уравнение Клапейрона-Менделеева
для произвольной массы газа
R = 8.31 Дж/(моль К) – универсальная газовая постоянная
m
- Количество вещества
p nkT
- Альтернативная запись уравнения состояния
k = 1.38·10-23 Дж/К – постоянная Больцмана
n
N
V
- концентрация, т.е. число молекул в единице объема
6

7.

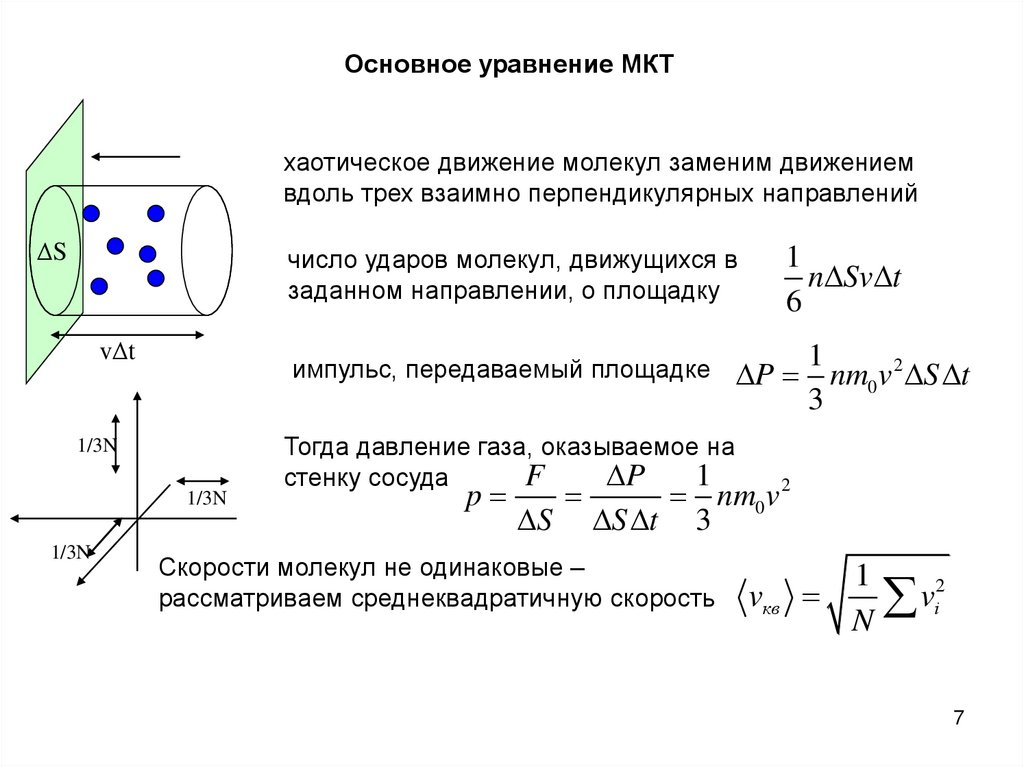
Основное уравнение МКТ
хаотическое движение молекул заменим движением
вдоль трех взаимно перпендикулярных направлений
ΔS
число ударов молекул, движущихся в
заданном направлении, о площадку
vΔt
импульс, передаваемый площадке
1/3N
1/3N
1/3N
1
n Sv t
6
1
P nm0 v 2 S t
3
Тогда давление газа, оказываемое на
F
P
1
стенку сосуда
p
S
nm0 v 2
S t 3
Скорости молекул не одинаковые –
рассматриваем среднеквадратичную скорость
vкв
1
2
v
i
N
7

8.

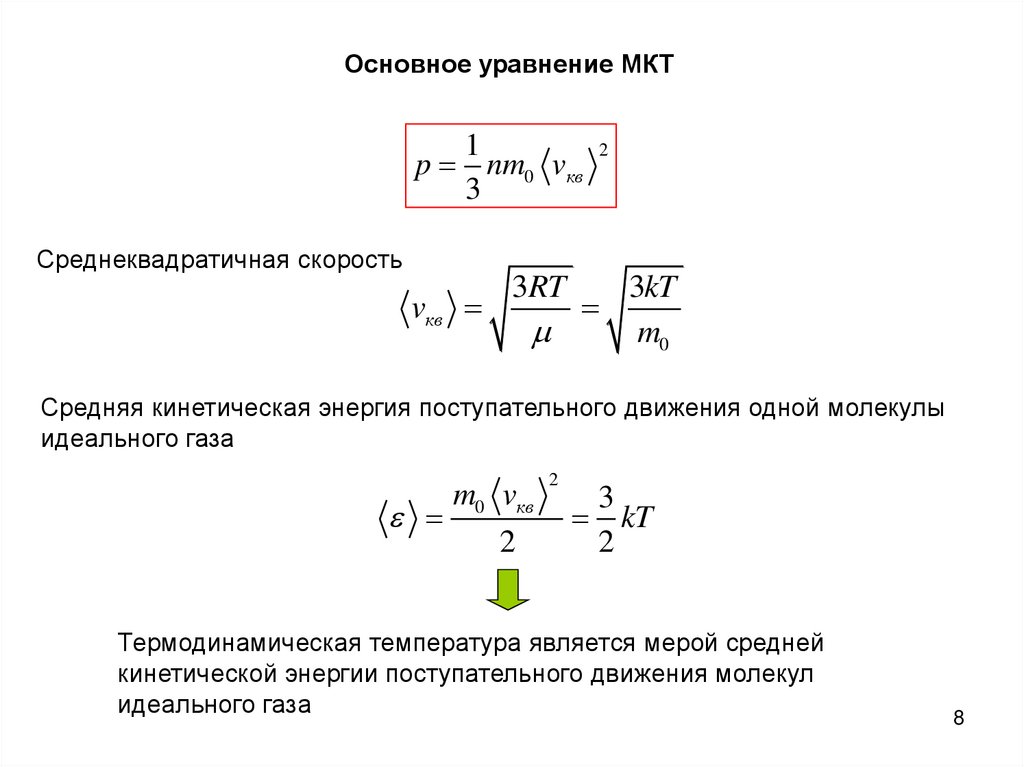
Основное уравнение МКТ
1
2
p nm0 vкв
3
Среднеквадратичная скорость
vкв
3RT
3kT
m0
Средняя кинетическая энергия поступательного движения одной молекулы
идеального газа
m0 vкв
2
2
3
kT
2
Термодинамическая температура является мерой средней
кинетической энергии поступательного движения молекул
идеального газа
8

9.

Молекулярно-кинетическая теория идеальных газов
По молекулярно-кинетической теории, как бы ни изменялись скорости
молекул при столкновениях, средняя квадратичная скорость молекул массой
m0 в газе, находящемся в состоянии равновесия при ( Т= const), остается
постоянной и равной <vкв>
В газе устанавливается некоторое стационарное, не меняющееся со
временем распределение молекул по скоростям, которое подчиняется
Закону Максвелла
Функция f(v) - функция распределения молекул по скоростям, определяет
относительное число (долю) молекул, скорости которых лежат в интервале от
v до v + dv
dN
f (v)dv
N
3/2
2
закон распределения молекул
m
m
v
0
2
0
f (v) 4
идеального газа по скоростям
v exp
2
kT
2
kT
f ( )
2
kT
3/2
функция распределения молекул по
exp
kT энергиям теплового движения
9

10.

Молекулярно-кинетическая теория идеальных газов
Закон Максвелла – внешние силы не действуют
Как ведут себя молекулы в поле тяготения Земли?
барометрическая формула позволяет найти атмосферное
давление в зависимости от высоты или, измерив давление,
найти высоту
g (h2 h1 )
p2 p1 exp
RT
gh h – высота над уровнем моря,
p p0 exp
RT р0 – давление на уровне моря
p nkT
m0 gh
распределение Больцмана для
n n0 exp
внешнего потенциального поля.
n0 exp
kT
kT
Если частицы имеют одинаковую массу и находятся в состоянии
хаотического теплового движения, то распределение Больцмана
справедливо в любом внешнем потенциальном поле, а не только в
поле сил тяжести.
10

11.

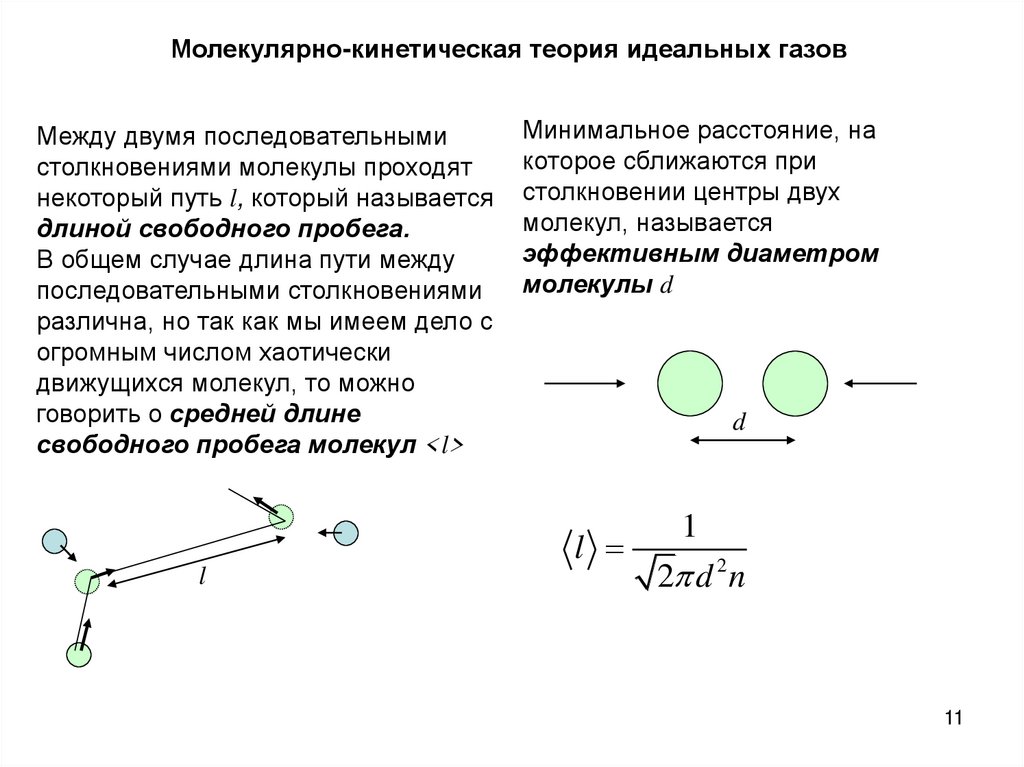
Молекулярно-кинетическая теория идеальных газов
Между двумя последовательными
столкновениями молекулы проходят
некоторый путь l, который называется
длиной свободного пробега.
В общем случае длина пути между
последовательными столкновениями
различна, но так как мы имеем дело с
огромным числом хаотически
движущихся молекул, то можно
говорить о средней длине
свободного пробега молекул <l>
l
Минимальное расстояние, на
которое сближаются при
столкновении центры двух
молекул, называется
эффективным диаметром
молекулы d
d
1
l
2 d 2 n
11

12.

явления переноса - процессы в результате которых
происходит пространственный перенос
теплопроводность обусловлена переносом энергии.
диффузия обусловлена переносом массы.
Если в одной области газа средняя кинетическая
энергия молекул больше, чем в другой, то с
течением времени происходит процесс
выравнивания средних кинетических энергий, т.е.,
иными словами, выравнивание температур.
Самопроизвольное проникновение и
перемешивание частиц двух соприкасающихся
газов, жидкостей и даже твердых тел; диффузия
сводится к обмену масс частиц этих тел,
возникает и продолжается, пока существует
градиент плотности.
Закон Фурье
jE
dT
dx
1
3
cV v l
jE – плотность теплового потока
внутреннее трение обусловлено переносом импульса.
Трение между параллельными слоями газа
(жидкости), движущимися с различными
скоростями. Из-за хаотического теплового
движения происходит обмен молекулами между
слоями, в результате чего импульс (и скорость)
слоев изменяется.
Закон Фика
jm D
d
dx
D
1
v l
3
jm – плотность потока массы
Закон Ньютона
F
dv
S
dx
1
3
v l
j p
dv
dx
jр – плотность потока импульса
12

13.

Основы Термодинамики
Внутренняя энергия U — энергия
хаотического (теплового) движения
микрочастиц системы и энергия
взаимодействия этих частиц.
Одноатомный газ i =3
Средняя энергия молекулы
i
kT
2
Число степеней свободы i –
число независимых величин,
полностью определяющих
положение системы в пространстве
Двухатомный газ i =5
Многоатомный газ i =6
Внутренняя энергия для произвольной
массы идеального газа
U
mi
i
RT RT
2
2
13

14.

Основы Термодинамики
Существует две формы передачи энергии от одних тел к другим: работа и
теплота. Энергия механического движения может превращаться в энергию
теплового движения, и наоборот. При этих превращениях соблюдается закон
сохранения и превращения энергии; применительно к термодинамическим
процессам - первое начало термодинамики
Q U A
Первое начало термодинамики: теплота, сообщаемая
системе, расходуется на изменение ее внутренней энергии и на
совершение ею работы против внешних сил.
14

15.

Основы Термодинамики
Элементарная работа, совершаемая газом при
изменении его объема
Работа, совершаемая газом при изменении его
объема от V1 до V2
dA pdV
V2
A pdV
V1
Удельная теплоемкость вещества — величина, равная количеству
теплоты, необходимому для нагревания 1 кг вещества на 1 К
c
dQ
mdT
Молярная теплоемкость — величина, равная количеству теплоты,
необходимому для нагревания 1 моль вещества на 1 К
dQ
C
dT
Связь удельной теплоемкости с молярной
C c
15

16.

Основы Термодинамики
Различают теплоемкости при постоянном объеме и постоянном давлении,
Изохорный процесс
CV
dQ dU pdV
dT
dT
V const
pdV 0
Изобарный процесс
dQ dU pdV
Cp
dT
dT
pdV
C p CV
dT
i
dU RdT
2
C p CV R
i
CV R
2
i 2
Cp
R
2
Уравнение Майера
16

17.

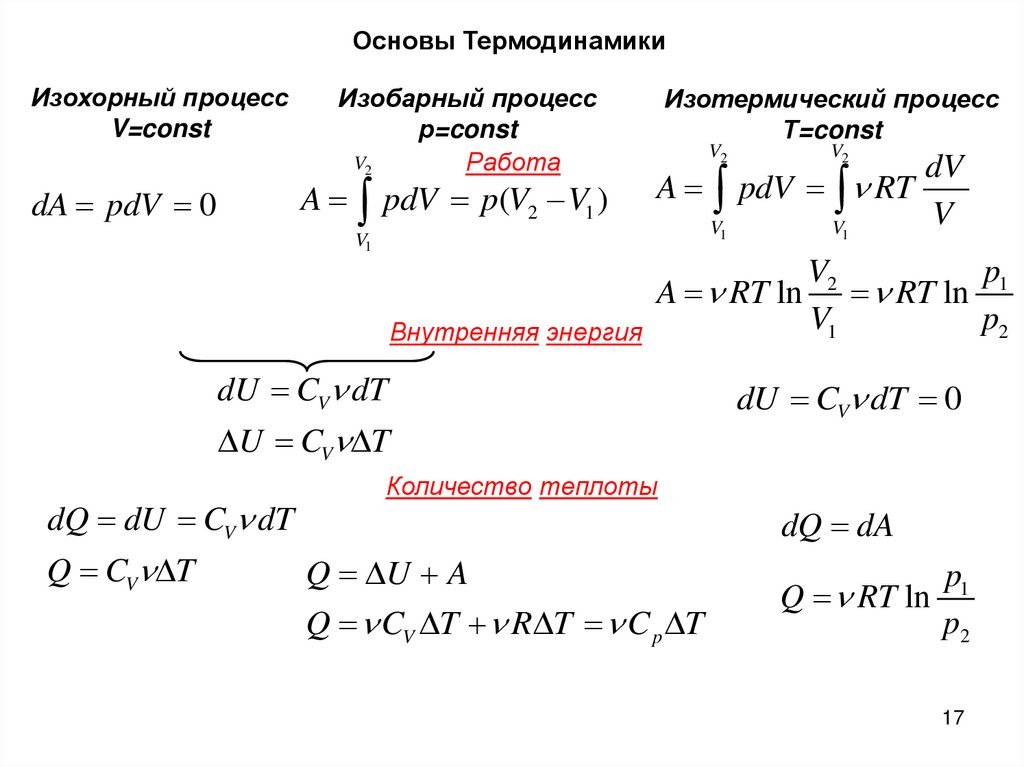
Основы Термодинамики
Изохорный процесс
V=const
Изобарный процесс
р=const
V2
Работа
A pdV p(V2 V1 )
dA pdV 0
V1
Изотермический процесс
Т=const
V2
V2
dV
A pdV RT
V
V1
V1
p1
V2
A RT ln RT ln
p2
V1
Внутренняя энергия
dU CV dT
U CV T
dQ dU CV dT
Q CV T
dU CV dT 0
Количество теплоты
dQ dA
Q U A
Q CV T R T C p T
p1
Q RT ln
p2
17

18.

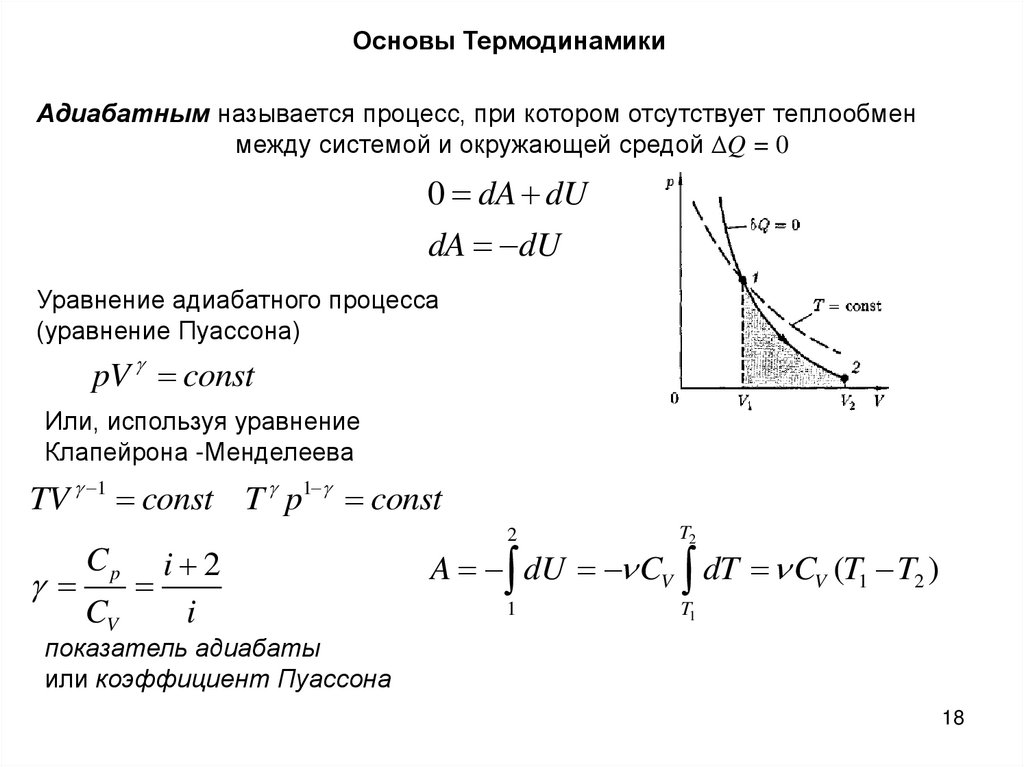
Основы Термодинамики
Адиабатным называется процесс, при котором отсутствует теплообмен
между системой и окружающей средой ΔQ = 0
0 dA dU
dA dU
Уравнение адиабатного процесса
(уравнение Пуассона)
pV const
Или, используя уравнение
Клапейрона -Менделеева
TV 1 const T p1 const
Cp
CV
i 2
i
2
T2
1
T1
A dU CV dT CV (T1 T2 )
показатель адиабаты
или коэффициент Пуассона
18

19.

Основы Термодинамики
Рассмотренные процессы имеют общую особенность —
они происходят при постоянной теплоемкости
Процесс, в котором теплоемкость остается постоянной,
называется политропным.
pV n const
n
C Cp
C CV
- Показатель политропы
все рассмотренные процессы являются частными
случаями политропного процесса
C n 1 получаем уравнение изотермы
pV const
pV const
C C p n 0 получаем уравнение изобары
p const
C 0 n
C CV n
получаем уравнение адиабаты
получаем уравнение изохоры
19

20.

Основы Термодинамики
Круговой процесс (цикл) - процесс, при котором система, пройдя через ряд
состояний, возвращается в исходное.
Работа А, совершаемая газом за цикл,
определяется площадью, охватываемой
замкнутой кривой
p
1
Если за цикл совершается положительная
работа (цикл протекает по часовой стрелке),
то он называется прямым, если за цикл
совершается отрицательная работа (цикл
протекает против часовой стрелки), то он
называется обратным
2
V
Прямой цикл используется в тепловых двигателях
Обратный цикл используется в холодильных машинах
термический коэффициент полезного действия для
кругового процесса
A Q1 Q2
Q1
Q1
20

21.

Основы Термодинамики
Энтропия - функция состояния, дифференциалом которой является
выражение
dS
Для обратимых
процессов
Q
T
S 0
Неравенство Клазиуса
энтропия замкнутой системы
S 0
может либо возрастать
Для необратимых S 0
(необратимые процессы),
процессов
либо оставаться постоянной
(обратимые процессы).
Энтропия незамкнутой системы может
вести себя любым образом
Если система совершает равновесный
переход из состояния 1 в состояние 2,
то изменение энтропии
2
S S2 S1
T2
V2
S CV ln R ln
T1
V1
1
Q
T
21

22.

Основы Термодинамики
Энтропия обладает свойством аддитивности: энтропия системы равна
сумме энтропий тел, входящих в систему
Термодинамическая вероятность состояния системы W — это число
способов, которыми может быть реализовано данное состояние
макроскопической системы, или число микросостояний, осуществляющих
данное макросостояние
S k ln W - формула Больцмана
Энтропия - мера вероятности состояния термодинамической системы.
Формула Больцмана позволяет дать энтропии следующее статистическое
толкование: энтропия является мерой неупорядоченности системы.
Принцип возрастания энтропии - все процессы в замкнутой
системе ведут к увеличению ее энтропии.
Процессы в замкнутой системе идут в направлении увеличения числа
микросостояний, иными словами, от менее вероятных состояний к
более вероятным
22

23.

Основы Термодинамики
Первое начало термодинамики
Q U A
закон сохранения и
превращения энергии
Второе начало термодинамики определяет направление
протекания термодинамических процессов
Закон возрастания энтропии замкнутой системы при необратимых
процессах: любой необратимый процесс в замкнутой системе происходит
так, что энтропия системы при этом возрастает.
Третье начало термодинамики
Теорема Нернста-Планка: энтропия всех тел в состоянии
равновесия стремится к нулю по мере приближения температуры к
нулю кельвин
lim S 0
T 0
23

24.

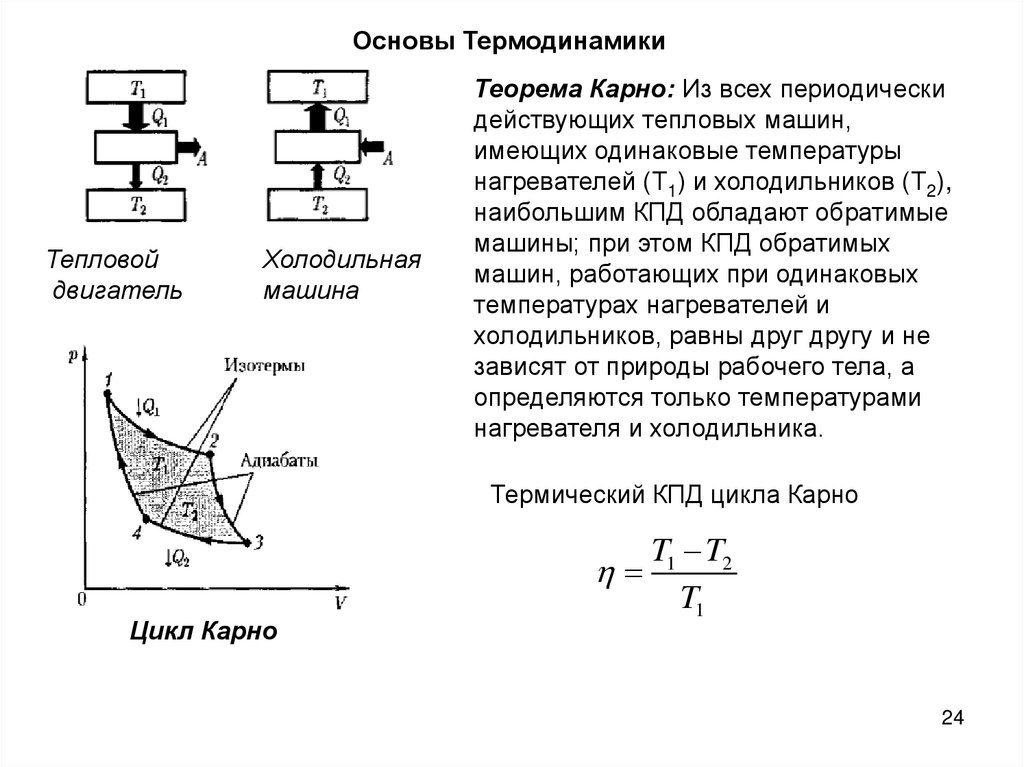
Основы Термодинамики
Тепловой
двигатель
Холодильная
машина
Теорема Карно: Из всех периодически
действующих тепловых машин,
имеющих одинаковые температуры
нагревателей (Т1) и холодильников (Т2),
наибольшим КПД обладают обратимые
машины; при этом КПД обратимых
машин, работающих при одинаковых
температурах нагревателей и
холодильников, равны друг другу и не
зависят от природы рабочего тела, а
определяются только температурами
нагревателя и холодильника.
Термический КПД цикла Карно
Цикл Карно
T1 T2
T1
24

25.

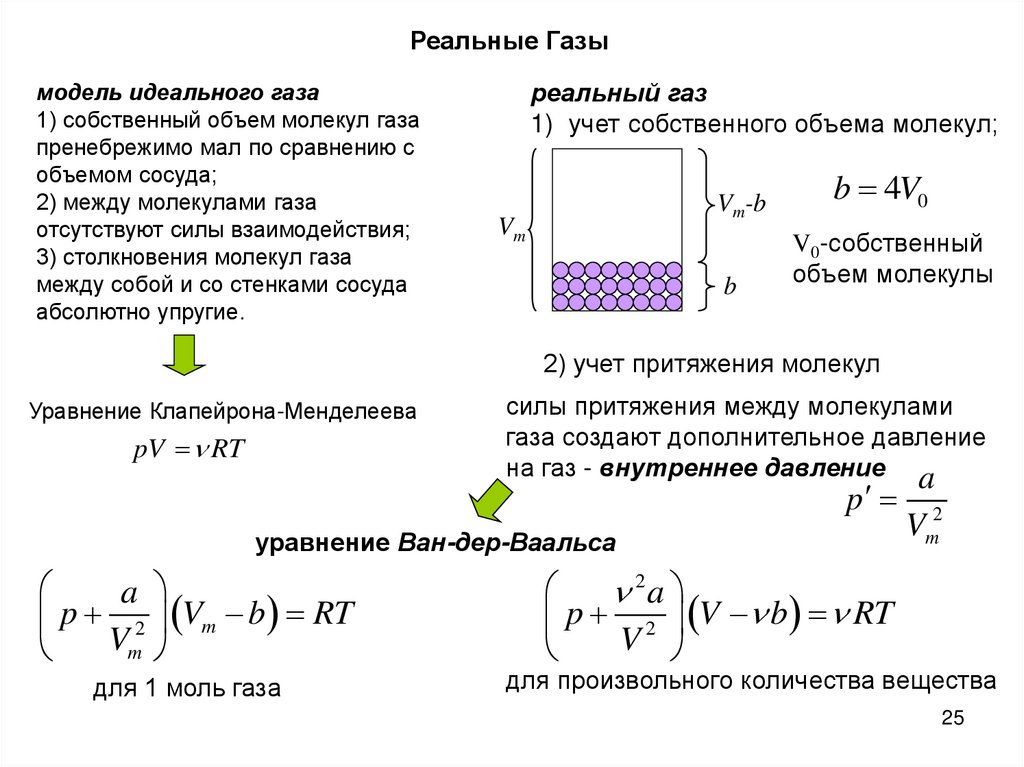
Реальные Газы
модель идеального газа
1) собственный объем молекул газа
пренебрежимо мал по сравнению с
объемом сосуда;
2) между молекулами газа
отсутствуют силы взаимодействия;
3) столкновения молекул газа
между собой и со стенками сосуда
абсолютно упругие.
реальный газ
1) учет собственного объема молекул;
Vm
Vm-b
b 4V0
b
V0-собственный
объем молекулы
2) учет притяжения молекул
Уравнение Клапейрона-Менделеева
pV RT
силы притяжения между молекулами
газа создают дополнительное давление
на газ - внутреннее давление a
p
уравнение Ван-дер-Ваальса
a
p 2 Vm b RT
Vm
для 1 моль газа
Vm2
2a
p 2 V b RT
V
для произвольного количества вещества
25

26.

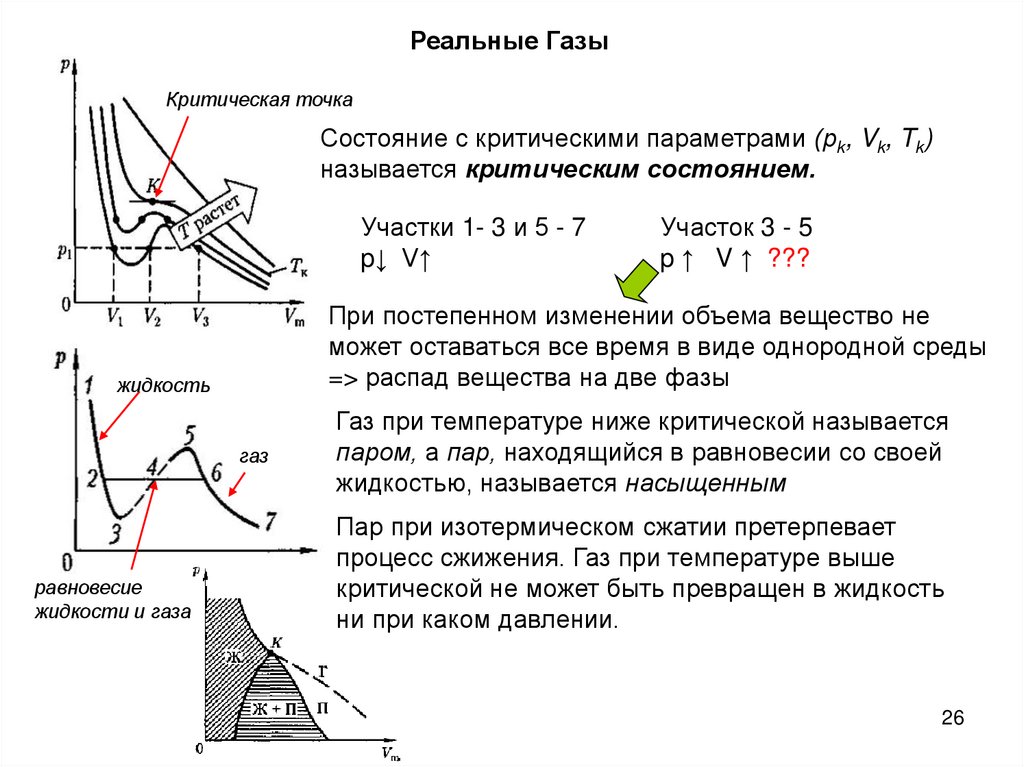
Реальные Газы
Критическая точка
Состояние с критическими параметрами (рk, Vk, Tk)
называется критическим состоянием.
Участки 1- 3 и 5 - 7
p↓ V↑
При постепенном изменении объема вещество не
может оставаться все время в виде однородной среды
=> распад вещества на две фазы
жидкость
газ
равновесие
жидкости и газа
Участок 3 - 5
p ↑ V ↑ ???
Газ при температуре ниже критической называется
паром, а пар, находящийся в равновесии со своей
жидкостью, называется насыщенным
Пар при изотермическом сжатии претерпевает
процесс сжижения. Газ при температуре выше
критической не может быть превращен в жидкость
ни при каком давлении.
26

27.

Реальные Газы
Внутренняя энергия реального газа складывается из кинетической энергии
теплового движения его молекул и потенциальной энергии межмолекулярного
взаимодействия. Для 1 моль реального газа имеем
U m CV T
a
Vm
Адиабатное расширение газа в вакуум
(ΔQ=0, A=0)
U1 U 2
при адиабатном расширении без совершения внешней работы внутренняя
энергия газа не изменяется.
идеальный газ
реальный газ
U1 U 2
T1 T2
при адиабатном
расширении идеального газа в
вакуум температура не
изменяется
T1 T2
a 1 1
CV V1 V2
при адиабатном расширении в вакуум
охлаждается. При адиабатном сжатии в
вакуум реальный газ нагревается
27

28.

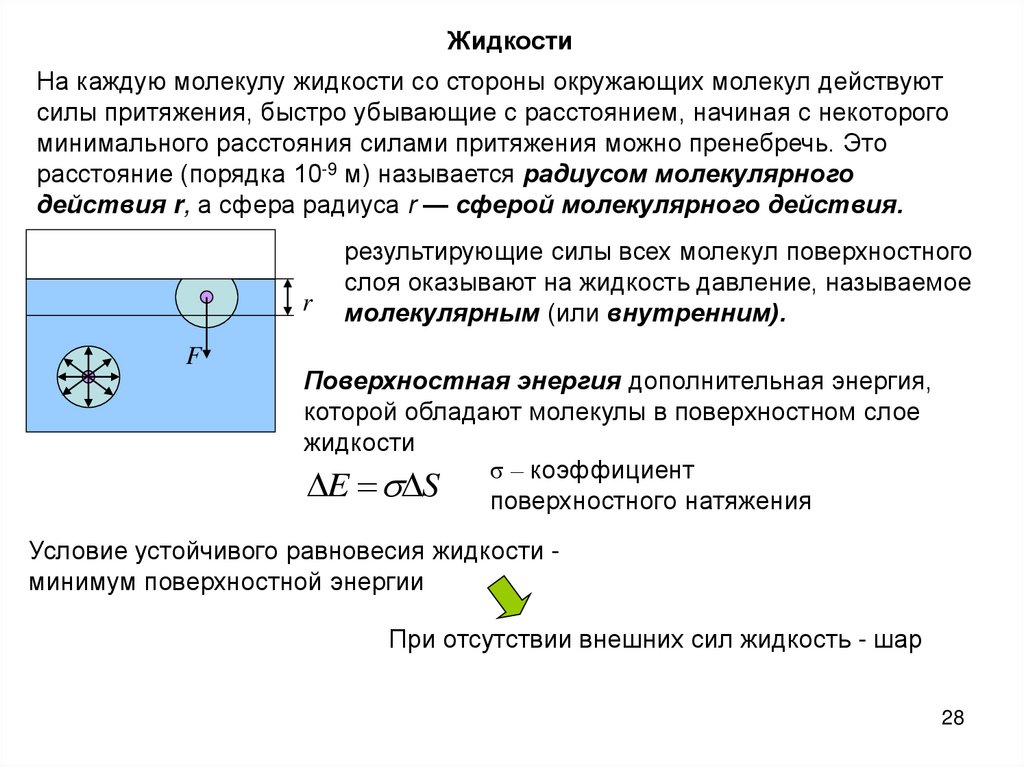
Жидкости
На каждую молекулу жидкости со стороны окружающих молекул действуют
силы притяжения, быстро убывающие с расстоянием, начиная с некоторого
минимального расстояния силами притяжения можно пренебречь. Это
расстояние (порядка 10-9 м) называется радиусом молекулярного
действия r, а сфера радиуса r — сферой молекулярного действия.
r
F
результирующие силы всех молекул поверхностного
слоя оказывают на жидкость давление, называемое
молекулярным (или внутренним).
Поверхностная энергия дополнительная энергия,
которой обладают молекулы в поверхностном слое
жидкости
σ – коэффициент
E S поверхностного натяжения
Условие устойчивого равновесия жидкости минимум поверхностной энергии
При отсутствии внешних сил жидкость - шар
28

29.

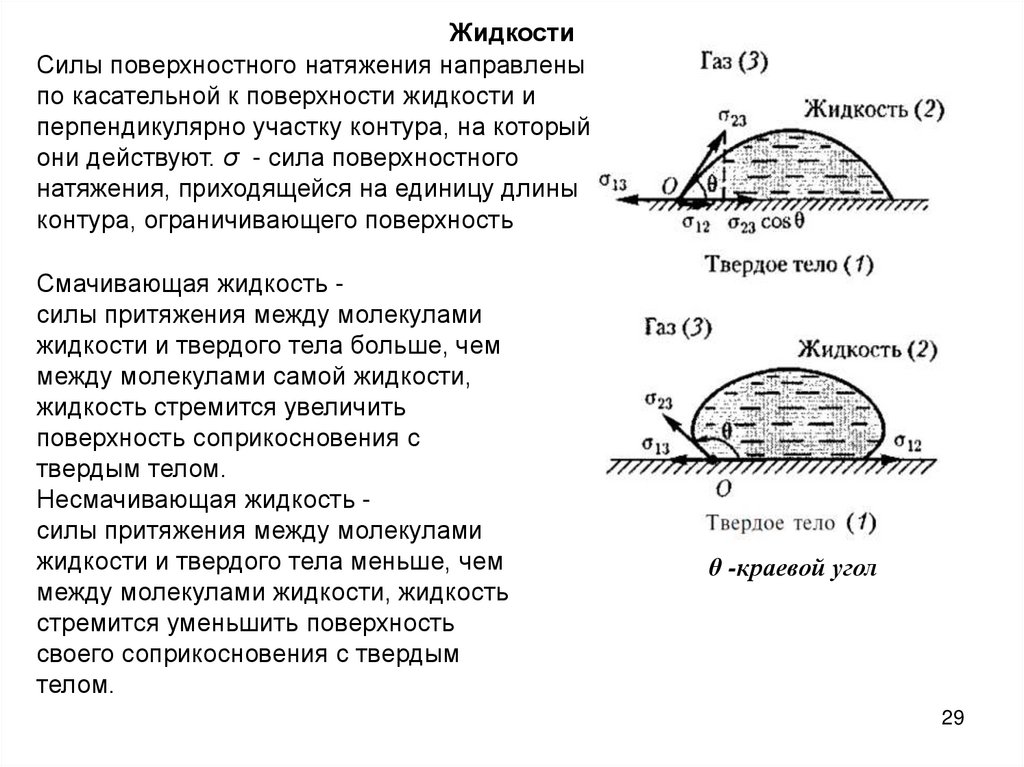
Жидкости
Силы поверхностного натяжения направлены
по касательной к поверхности жидкости и
перпендикулярно участку контура, на который
они действуют. σ - сила поверхностного
натяжения, приходящейся на единицу длины
контура, ограничивающего поверхность
Смачивающая жидкость силы притяжения между молекулами
жидкости и твердого тела больше, чем
между молекулами самой жидкости,
жидкость стремится увеличить
поверхность соприкосновения с
твердым телом.
Несмачивающая жидкость силы притяжения между молекулами
жидкости и твердого тела меньше, чем
между молекулами жидкости, жидкость
стремится уменьшить поверхность
своего соприкосновения с твердым
телом.
θ -краевой угол
29

30.

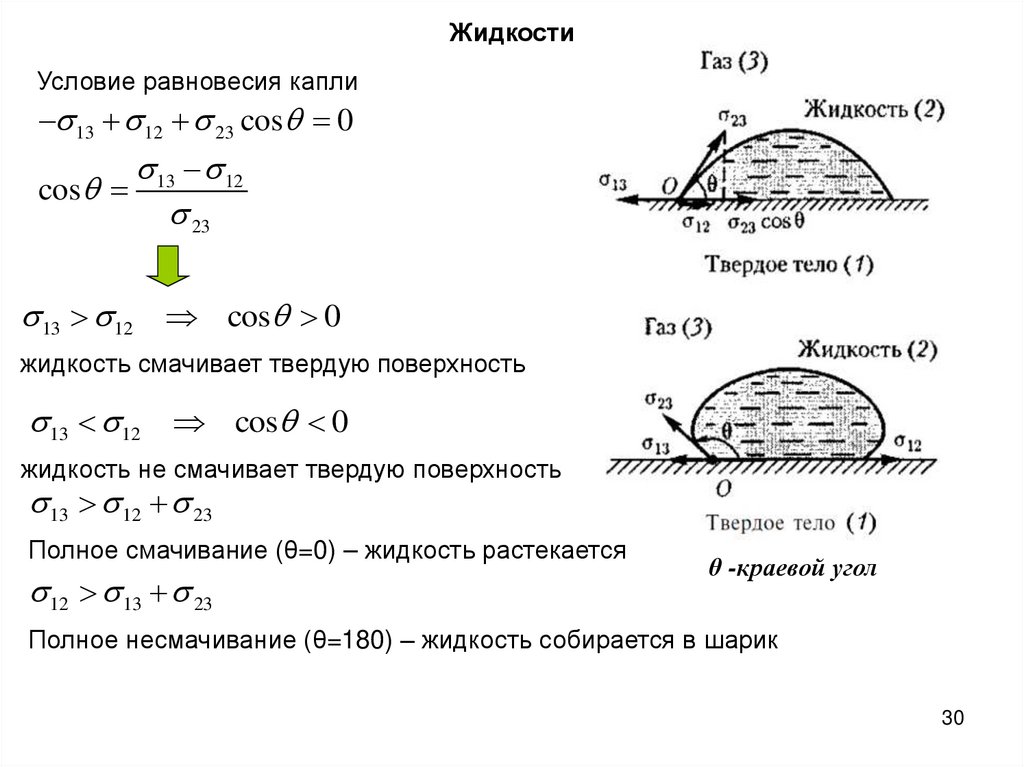
Жидкости
Условие равновесия капли
13 12 23 cos 0
13 12
cos
23
13 12 cos 0
жидкость смачивает твердую поверхность
13 12 cos 0
жидкость не смачивает твердую поверхность
13 12 23
Полное смачивание (θ=0) – жидкость растекается
12 13 23
θ -краевой угол
Полное несмачивание (θ=180) – жидкость собирается в шарик
30

31.

Жидкости
Если поверхность жидкости не плоская, а искривленная, то она оказывает на
жидкость избыточное (добавочное) давление. Это давление, обусловленное
силами поверхностного натяжения, для выпуклой поверхности положительно, а
для вогнутой — отрицательно
Избыточное давление для произвольной поверхности жидкости двоякой
кривизны
1 1
p
R1 R2
R1 и R2 – радиусы кривизны поверхности
Радиус кривизны положителен, если центр кривизны соответствующего
сечения находится внутри жидкости, и отрицателен, если центр кривизны
находится вне жидкости
Для сферической искривленной
поверхности
2
p
( R1 R2 R )
R
Для цилиндрической
искривленной поверхности
p
R
( R1 R, R2 )
31

32.

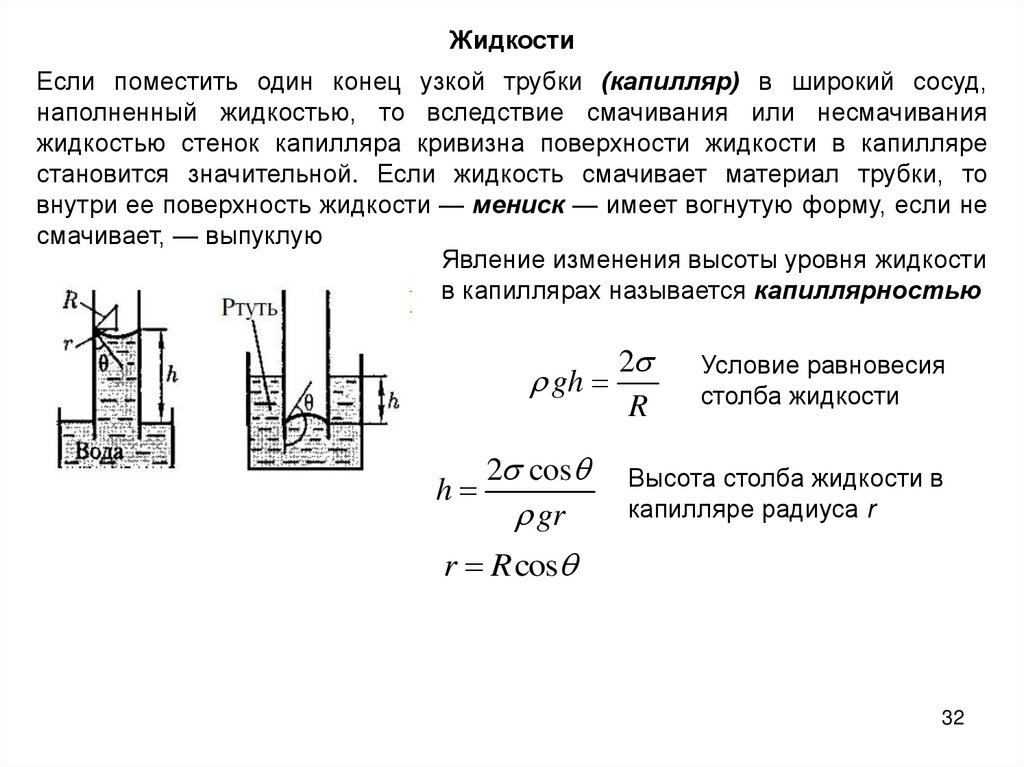
Жидкости
Если поместить один конец узкой трубки (капилляр) в широкий сосуд,
наполненный жидкостью, то вследствие смачивания или несмачивания
жидкостью стенок капилляра кривизна поверхности жидкости в капилляре
становится значительной. Если жидкость смачивает материал трубки, то
внутри ее поверхность жидкости — мениск — имеет вогнутую форму, если не
смачивает, — выпуклую
Явление изменения высоты уровня жидкости
в капиллярах называется капиллярностью
gh
h
2 cos
gr
2
R
Условие равновесия
столба жидкости
Высота столба жидкости в
капилляре радиуса r
r R cos
32