Молекулярная физика и термодинамика

1.

Молекулярная физика и термодинамика
Молекулярная физика и термодинамика — разделы физики, в которых
изучаются физические свойства тел (газы, жидкости, тв. тела) на основе
молекулярных представлений.
Все тела состоят из атомов и молекул. Атомы и молекулы
взаимодействуют друг с другом и находятся в непрерывном движении.
Существует 2 метода изучения:
company name
1. Статистический метод (молекулярно-кинетический) - свойства
макроскопической системы в конечном счете определяются свойствами
частиц системы, особенностями их движения и усредненными
значениями динамических характеристик этих частиц (скорости, энергии
и т.д.)
Молекулярная физика - раздел физики, в котором изучаются строение и
свойства вещества исходя из молекулярно-кинетических представлений,
основывающихся на том, что все тела состоят из молекул, находящихся в
непрерывном хаотическом движении.

2.

Термодинамика
2. Термодинамический метод не рассматривает микропроцессы.
Термодинамика - раздел физики, в котором изучаются общие свойства
макроскопических систем, находящихся в состоянии термодинамического
равновесия, и процессы перехода между этими состояниями.
Термодинамическая система - совокупность макроскопических тел,
которые взаимодействуют и обмениваются энергией как между собой, так
и с другими телами (внешней средой).
company name
Состояние системы задается термодинамическими параметрами
(параметрами состояния) - совокупностью физических величин,
характеризующих свойства термодинамической системы (температура,
давление, удельный объем).
Типы термодинамических параметров
экстенсивные
(пропорциональны
количеству
вещества в системе )
объем, внутренняя энергия
интенсивные
(не зависят от кол-ва вещества и
массы системы)
давление, температура

3.

Основные понятия
Удельный объем - объем единицы массы:
V уд
V 1
m
Давление создается ударами беспорядочно движущихся молекул:
company name
Температура
физическая
величина,
характеризующая состояние термодинамического
равновесия макроскопической системы.
2
основные
термодинамическая
практическая (оС).
температурные
шкалы:
(К)
и
Международная
T K t 273,15 C

4.

Идеальный газ
Модель идеального газа:
1) Собственный
объем
молекул
газа
пренебрежимо мал по сравнению с объемом
сосуда.
2) Между молекулами газа отсутствуют силы
взаимодействия.
3) Столкновения молекул газа между собой и со
стенками сосуда абсолютно упругие.
Воздух при н.у. t 0 C , p 10 Па можно считать идеальным газом,
cредняя длина свободного пробега
молекул
, эффективный
700
A
диаметр молекул воздуха 3 A .
company name
5
Уравнение состояния произвольного кол-ва
идеального газа.
Уравнение Клапейрона-Менделеева (1874 г.)
связывает параметры состояния ид. газа:
давление, объем, температуру.
M - масса газа,
- молярная масса.
pV
M
RT
R - унив. газовая const
R 8,31
Дж
моль K

5.

Идеальный газ
Другие варианты записи уравнения
состояния идеального газа
M
- количество вещества
pV RT
p RT
M RT
N RT N R
p
T
V
Na V
V Na
M
- плотность газа
V
M
pV
RT
company name
N
n - числовая плотность газа
V
R
k
- постоянная Больцмана
Na
p nkT
k 1,38 10 23
Дж
K

6.

Основное уравнение молекулярно-кинетической теории идеальных газов
Основное уравнение МКТ выражает связь
давления газа со средней кинетической
энергией поступательного движения молекул
При упругом соударении со
молекула передает ей импульс:
m0V m0V 2m0V
стенкой
За время t площадки S достигнут те молекулы, которые находятся
в объеме цилиндра с S и высотой V t :
N n S V t
V S l S V t
company name
n - число молекул в единице объема,
S - площадь поверхности стенки,
l V t - путь, пройденный молекулой за время t .
Число ударов молекул о стенку:
n S V t
6

7.

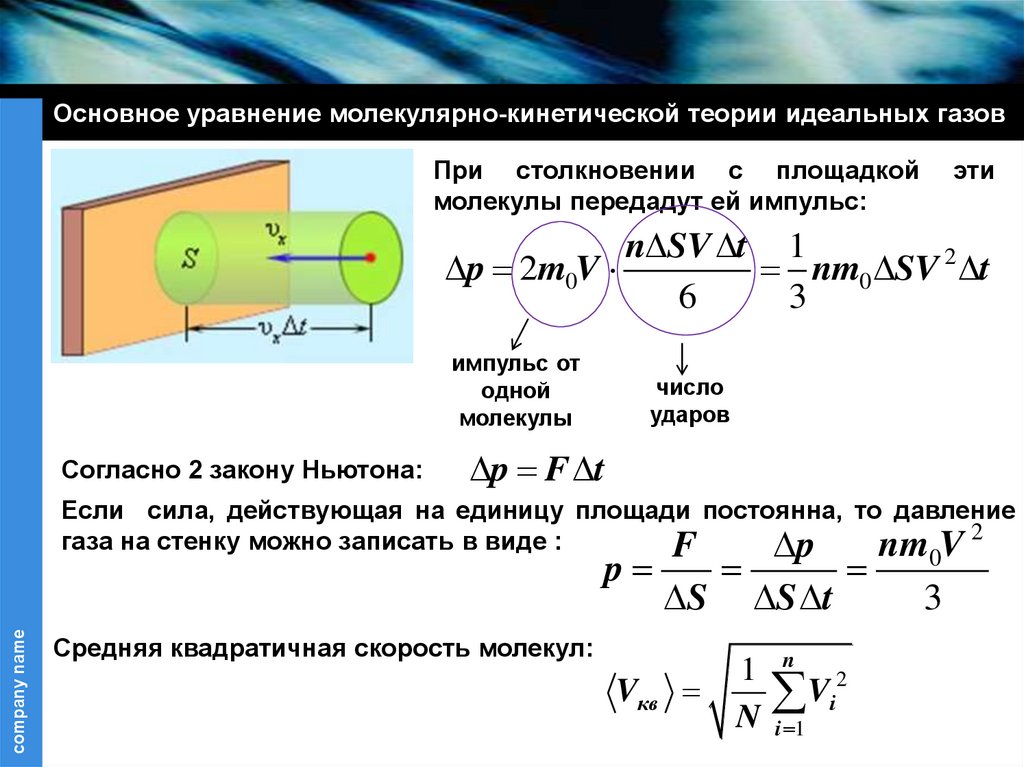
Основное уравнение молекулярно-кинетической теории идеальных газов
При столкновении с площадкой
молекулы передадут ей импульс:
эти
n SV t 1
p 2m0V
nm0 SV 2 t
6
3
импульс от
одной
молекулы
Согласно 2 закону Ньютона:
число
ударов
p F t
Если сила, действующая на единицу площади постоянна, то давление
газа на стенку можно записать в виде :
nm V 2
F
p
company name
p
S
Средняя квадратичная скорость молекул:
Vкв
S t
1 n 2
Vi
N i 1
0
3

8.

Основное уравнение молекулярно-кинетической теории идеальных газов
Давление газа, оказываемое на стенку
сосуда:
1
2
p nm0 Vкв
3
основное уравнение молекулярнокинетической теории ид. газов
m0 Vкв
wкин
- средняя кинетическая энергия поступательного
движения одной молекулы
N wкин Wкин
- кинетическая энергия поступательного движения
всех молекул
2
company name
2
2
pV Wкин
3
произведение давления газа на его объем равно
двум
третям
кин.
энергии
хаотического
поступательного движения всех его молекул

9.

Основное уравнение молекулярно-кинетической теории идеальных газов
Молекулярно – кинетический смысл температуры
Сопоставим уравнение
идеального газа:
состояния
p nkT
1
2
p nm0 Vкв
3
company name
средняя квадратичная скорость
молекул
k
R
- const Больцмана
Na
R
- унив. газовая const
T
- абсолютная температура
m0
Na
- масса одной молекулы
и
основное
Vкв
2
Vкв
уравнение
МКТ
3kT
m0
Vкв
2
Vкв
3kT
m0
3 RT
- молярная масса

10.

Основное уравнение молекулярно-кинетической теории идеальных газов
Молекулярно – кинетический смысл температуры
Сопоставим уравнение
идеального газа:
состояния
p nkT
1
2 m Vкв
2
p nm0 Vкв n
3
3
2
m Vкв
company name
2
2
Wкин
2
p n Wкин
3
2
и
основное
уравнение
МКТ
3
Wкин kT
2
Средняя
кинетическая
энергия
поступательного движения молекул
определяется только температурой
и не зависит от массы молекул, т.е.
температура есть количественная
мера энергии теплового движения
молекул.

11.

Основное уравнение молекулярно-кинетической теории идеальных газов
Кинетическая энергия всех молекул Wкин
Средняя кин. энергия поступательного дв-я
одной молекулы
3
wкин kT
2
Средняя кин. энергия поступательного дв-я
всех молекул
Wкин N wкин
N
- число молекул газа
company name
M
N Na
Na
M
3
3M
Wкин
Na kT
RT
2
2
Температура
–
мера
средней
кинетической
энергии
поступательного движения молекул газа.
Температура – характеристика всего газа, нельзя говорить о
температуре одной молекулы!!!

12.

Распределение Максвелла
company name
Распределение молекул по скоростям

13.

Распределение Максвелла
Распределение молекул идеального газа по скоростям и энергиям
теплового движения
Средняя квадратичная скорость молекул в газе, находящемся в
состоянии равновесия, остается постоянной:
T const
Vкв
Vкв
2
3kT
const
m0
В равновесном состоянии макроскопические параметры (P, V, T)
остаются постоянными, а микросостояния меняются.
company name
Средняя кинетическая энергия поступательного движения молекул:
Wкин
m0 Vкв
2
2
3
kT
2
Vкв
3 RT

14.

Распределение Максвелла
В равновесном состоянии распределение молекул по скоростям стационарное. Направления движения равновероятны, а абсолютные
значения – нет.
Пусть V - малый интервал, тогда число молекул,
приходящихся на него - N V
N (V ) f V N V
f V - функция распределения
молекул по скоростям
N
V
- общее число молекул
- интервал значений
скоростей
company name
Перейдя к пределу , получим
dN V f V NdV
Физический смысл f V в том, что это отношение числа молекул,
скорости которых лежат в определенном интервале скоростей, к
общему числу молекул в единичном интервале скоростей:

15.

Распределение Максвелла
Физический смысл
f V в том, что это отношение числа молекул,
скорости которых лежат в определенном интервале скоростей, к
общему числу молекул в единичном интервале скоростей:
f V
f V
dN V
NdV
m0V 2
A V 2e 2kT
m0
A 4
2
kT
company name
m0
f V 4
2
kT
, где
32
Множитель A находят из условия
нормировки:
f V dV 1
0
32
m0V 2
V 2 e 2 kT
закон распределения молекул
идеального газа по скоростям

16.

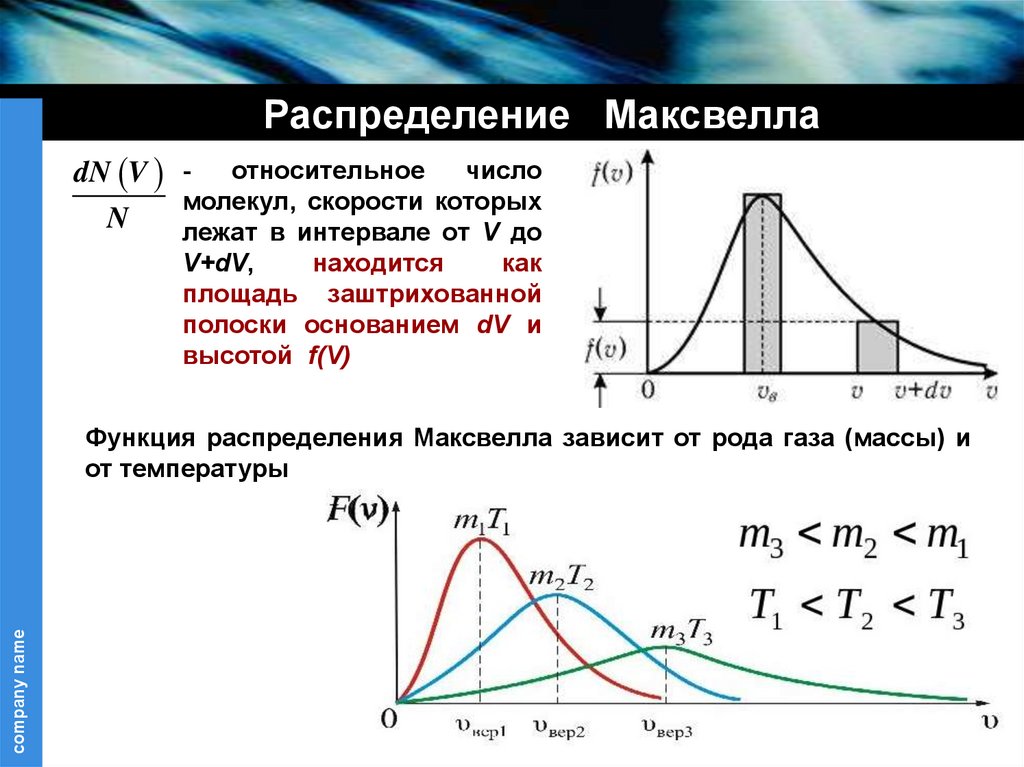
Распределение Максвелла
dN V N
относительное
число
молекул, скорости которых
лежат в интервале от V до
V+dV,
находится
как
площадь заштрихованной
полоски основанием dV и
высотой f(V)
company name
Функция распределения Максвелла зависит от рода газа (массы) и
от температуры

17.

Распределение Максвелла
Vв
- наиболее вероятная
скорость молекул
V
- средняя
молекул
Vкв
средняя
квадратичная
скорость молекул
f V 0
'
f V dV
company name
0
скорость
2kT
Vв
m0
8kT
V
m0
V f V dV
0
Vкв
3kT
m0

18.

Закон равномерного распределения энергии по степеням свободы
company name
Степенями
свободы
называются
независимые
координаты
(перемещения), полностью описывающие положение (движение) тела
в пространстве.
Число степеней свободы - i .
В жестких молекулах атомы не смещаются относительно друг друга.
В нежестких молекулах атомы могут смещаться относительно друг
друга. К имеющимся поступательным и вращательным степеням
свободы добавляются колебательные степени свободы.
Колебательные степени свободы характеризуют внутренние движения
атомов в молекуле, их учет необходим при высоких температурах.

19.

Закон равномерного распределения энергии по степеням свободы
Средняя
кинетическая
поступательного движения
молекулы
энергия
одноатомной
Число степеней
молекулы
одноатомной
свободы
3
wкин kT
2
i 3
У любой молекулы, независимо от общего числа степеней свободы,
3 – всегда поступательные, поэтому на каждую степень в среднем
должна приходиться одинакова я энергия, равная 1/3 общей.
company name
Средняя
кинетическая
энергия,
приходящаяся на одну степень свободы
Средняя кинетическая
возможных движений
целого
энергия всех
молекулы как
wкпост
3
kT
2
1
kT
3
2
iпост
wк
kT
iпост iвращ
2

20.

Закон равномерного распределения энергии по степеням свободы
Закон равномерного распределения энергии по
степеням свободы
На каждую поступательную степень свободы
молекулы приходится в среднем одинаковая
кинетическая энергия, равная
company name
Средняя кинетическая энергия
жестко связанными атомами:
молекулы,
с
1
kT
2
wк
ikT
2
Жесткой связи между атомами не существует, поэтому для реальных
молекул необходимо учитывать также степени свободы колебательного
движения.
Колебательная степень обладает вдвое большей энергией потому,
что на нее приходится не только кинетическая, но и потенциальная
энергия, причем средние значения кин. и потен. энергий одинаковы.
На каждую колебательную степень свободы – в среднем приходится
энергия равная kT.

21.

Закон равномерного распределения энергии по степеням свободы
i iпост iвращ 2iкол
полное число степеней свободы для
молекулы газа:
полная средняя энергия всех
возможных движений
молекулы:
kT
w iпост iвращ 2iкол
2
Внутренняя энергия идеального газа
энергия всевозможных видов движений и взаимодействия всех
частиц, образующих рассматриваемую систему
company name
Идеальный газ – газ, молекулы которого не
взаимодействуют друг с другом, т.е. их w п 0
U wкин
kT
U N w N i
2
число молекул газа
число всех степеней свободы молекулы

22.

Внутренняя энергия идеального газа
kT
U N w N i
2
M
M i
N Na
Na
U
RT
2
kNa R - универсальная газовая const
M i
U
RT
2
company name
внутренняя энергия является функцией
данного состояния системы
Зависит только от T и не зависит от P и V и складывается из
кинетической энергии молекул (величина аддитивная).
Изменение внутренней энергии определяется только ее начальным
и конечным состоянием, не зависит от процесса перехода.

23.

Реальный газ
Уравнение Ван-дер-Ваальса (1873 г.)
Исходные положения:
1) учитываются собственные
размеры молекул
Молекулы – абсолютно твердые
шарики, сферы с диаметром d эфф
company name
2) учитываются взаимодействия молекул
Между молекулами действуют силы притяжения
при r r0 .
При столкновениях молекул возникают силы
отталкивания.
r0
- положение устойчивого равновесия - положение, при
котором сила отталкивания равна силе притяжения.

24.

Реальный газ
company name
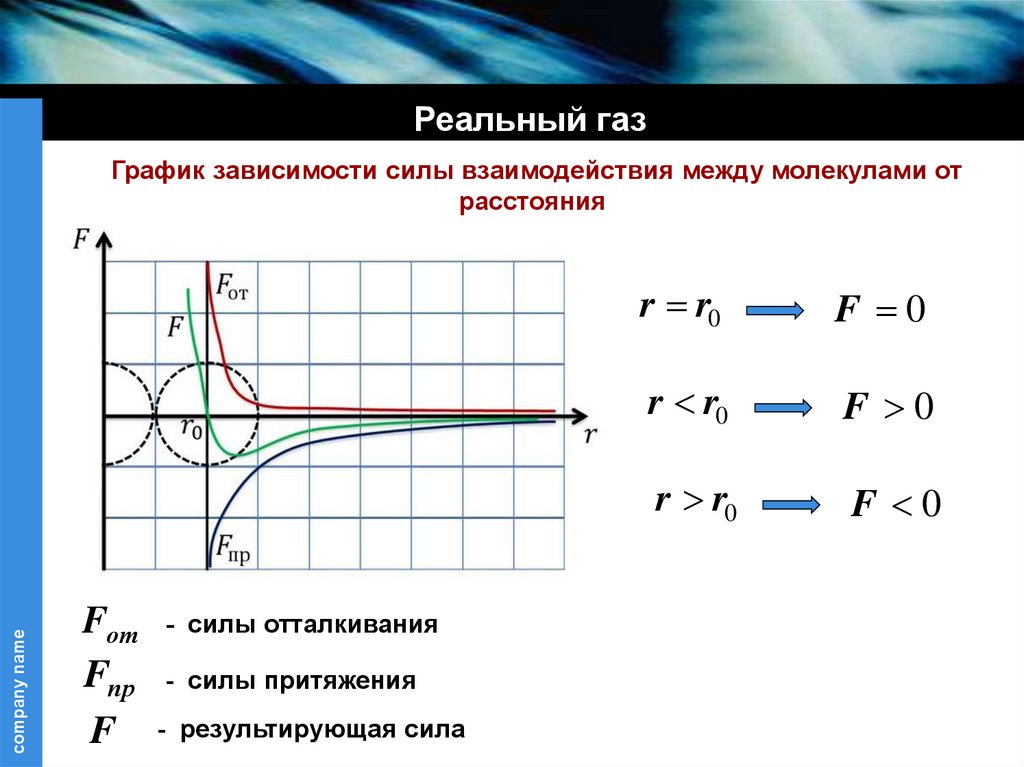
График зависимости силы взаимодействия между молекулами от
расстояния
Fот - силы отталкивания
Fпр - силы притяжения
F - результирующая сила
r r0
F 0
r r0
F 0
r r0
F 0

25.

company name
Реальный газ
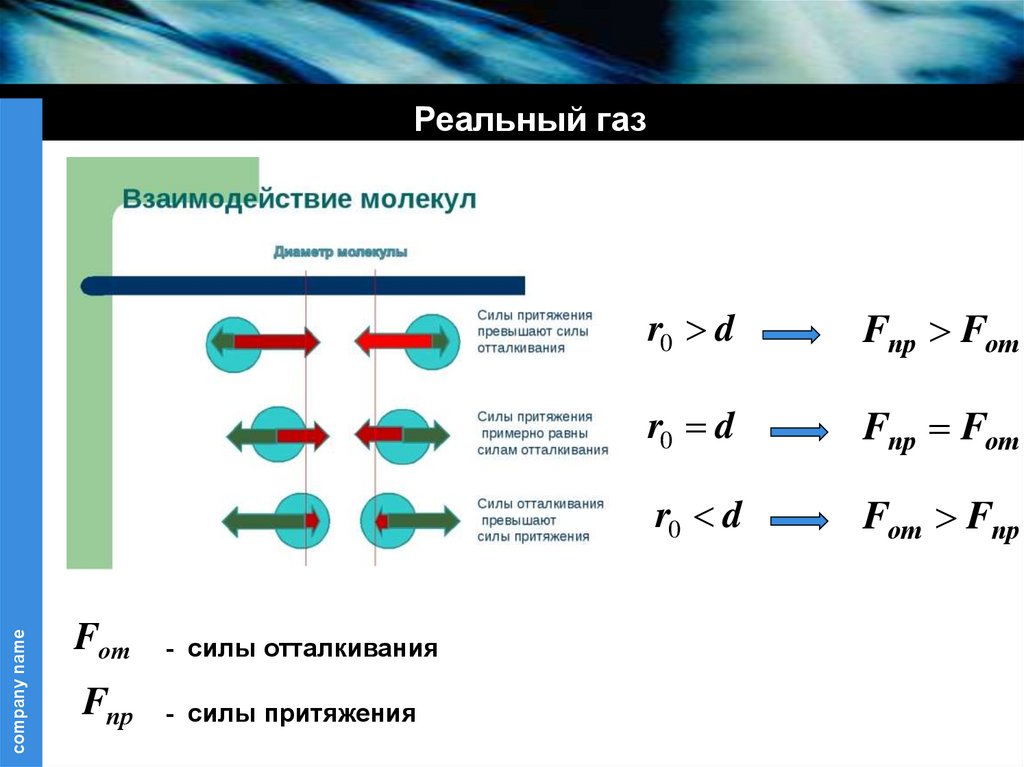
Fот
- силы отталкивания
Fпр
- силы притяжения
r0 d
Fпр Fот
r0 d
Fпр Fот
r0 d
Fот Fпр

26.

Реальный газ
company name
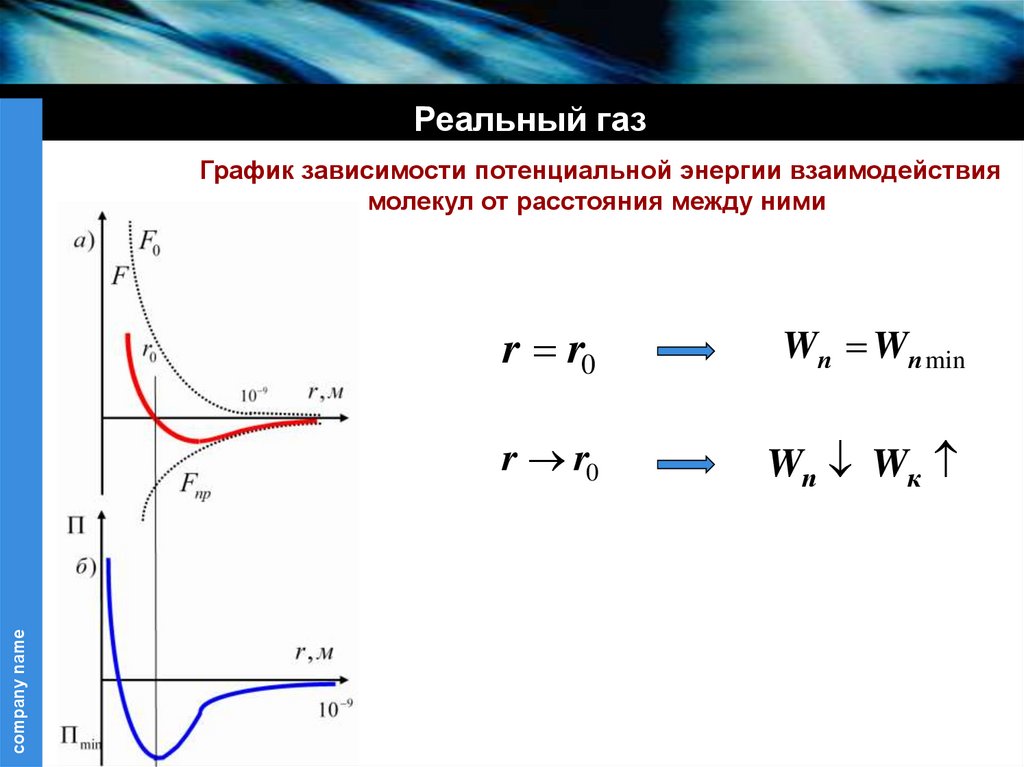
График зависимости потенциальной энергии взаимодействия
молекул от расстояния между ними
r r0
Wп Wп min
r r0
Wп Wк

27.

Реальный газ
Критерием различных агрегатных состояний вещества является
соотношение между величинами W п min и
kT
W п min
kT
company name
Если
- наименьшая потенциальная энергия взаимодействия
(определяет работу, которую нужно совершить против
сил притяжения для того, чтобы разъединить молекулы,
находящиеся в равновесии )
определяет
удвоенную
среднюю
энергию,
приходящуюся на одну степень свободы хаотического
(теплового) движения молекул
Wп min
kT
газообразное состояние
Wп min
kT
твердое тело
Wп min
kT
жидкость

28.

Реальный газ
Уравнение Ван-дер-Ваальса (1873 г.)
основывается
на
уравнении
состояния идеального газа
PVm RT
Уравнение Ван-дер-Ваальса для 1 моля газа:
a
P 2 Vm b RT
Vm
P'
a
- внутреннее давление
2
Vm
company name
Уравнение Ван-дер-Ваальса для произвольной массы газа:
M 2 a
M M
RT RT
P 2 2 V b
V
V - объем всей массы газа
V V
Vm
M

29.

Реальный газ
Уравнение Ван-дер-Ваальса (1873 г.)
a
P 2 V b RT
V
a, b
- постоянные Ван-дер-Ваальса (учитывают взаимодействие и
размеры молекул), определяются экспериментально
a
P 2
Vm
'
company name
b
- внутреннее давление (добавка к внешнему давлению),
учитывает взаимное притяжение молекул
- учитывает собственный объем, занимаемый молекулами газа
V b -
«свободный объем», объем доступный для движения
молекул (меньше полного объема сосуда)

30.

Реальный газ
При малых плотностях уравнение Ван-дер-Ваальса
уравнение состояния идеального газа
a
P 2 V b RT
V
a
0
2
0
при
V
V
V b
переходит в
PV RT
company name
Внутренняя энергия реального газа
Внутренняя энергия реального газа состоит из кинетической
энергии движения молекул W кин и потенциальной энергии их
взаимодействия W пот
U Wкин Wпот

31.

Реальный газ
U Wкин Wпот
р.г .
ид. г .
Wкин
Wкин
M
ид. г .
Wкин
i
RT
2
межмолекулярное взаимодействие не
влияет на движение молекул, т.е. W кин
молекул реального газа равна Wкин
идеального газа
M
р. г .
Wкин
cv T
i
R cv
2
Wпот - потенциальная энергия
V
A dA PdV
dW dA PdV
company name
V
2
M a
P Pвнутр 2
V

32.

Реальный газ
Wпот - потенциальная энергия
dW dA PdV
V
V
потенциальную
энергию
взаимодействия молекул определим
как работу против сил взаимного
притяжения молекул
A dA PdV
M
р. г .
Wпот
2
a
dV
2
V
company name
M a
P Pвнутр 2
V
M
р. г .
Wпот
2V
2
V
2
M a
a
V
V

33.

Реальный газ
Внутренняя энергия
произвольного количества
реального газа
2
U
M a
M i
RT
2
V
i
a
U RT
2
V
Внутренняя энергия 1 моля
реального газа
U f T , V
company name
В изохорном процессе (V=const) изменение внутренней энергии
реального газа определяется как и для идеального газа
р. г .
Wкин
const
M
dU
cv dT

34.

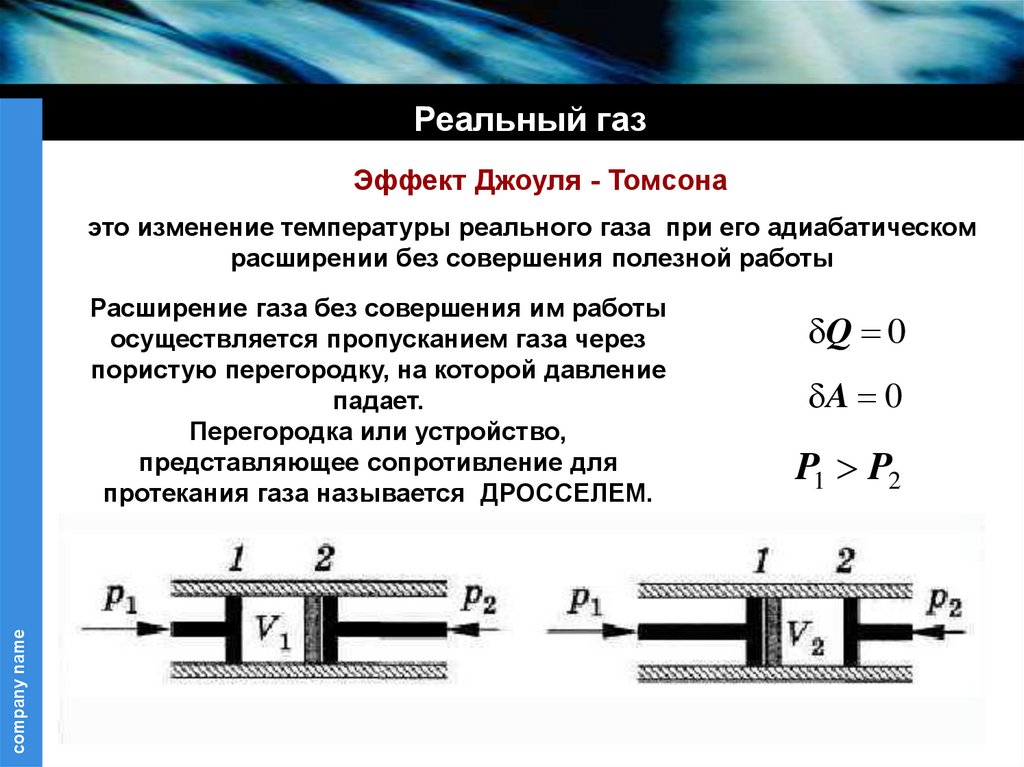
Реальный газ
Эффект Джоуля - Томсона
это изменение температуры реального газа при его адиабатическом
расширении без совершения полезной работы
company name
Расширение газа без совершения им работы
осуществляется пропусканием газа через
пористую перегородку, на которой давление
падает.
Перегородка или устройство,
представляющее сопротивление для
протекания газа называется ДРОССЕЛЕМ.
Q 0
A 0
P1 P2

35.

Реальный газ
Эффект Джоуля - Томсона
Эффект Джоуля – Томсона объясняется тем, что Wпот зависит от
среднего расстояния между молекулами, т.е. от плотности газа.
Адиабатическое расширение газа без совершения работы
происходит без изменения внутренней энергии.
dU 0
U Wкин Wпот
company name
dWкин dWпот
Для идеального газа эффект отсутствует.
Для реального газа эффект может быть как положительным , так
и отрицательным.

36.

Реальный газ
Эффект Джоуля - Томсона
Если в процессе адиабатического дросселирования :
а) плотность газа (межмолекулярные расстояния) изменилась так, что
потенциальная энергия взаимодействия молекул уменьшилась, то
увеличивается кинетическая энергия и увеличивается температура
dWпот 0
dWкин 0
dT 0
Отрицательный эффект Джоуля - Томсона
company name
а) плотность газа (межмолекулярные расстояния) изменилась так, что
потенциальная энергия взаимодействия молекул увеличилась, то
уменьшается кинетическая энергия и уменьшается температура
dWпот 0
dWкин 0
dT 0
Положительный эффект Джоуля - Томсона

37.

Реальный газ
Эффект Джоуля - Томсона
dWпот 0
dWкин 0
dT 0
company name
Отрицательный эффект Джоуля - Томсона
dWпот 0
dWкин 0
Положительный эффект Джоуля - Томсона
dT 0