Закон больших чисел. Лекция 7

1.

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Теория вероятностей и математическая статистика
лектор Макеева О.В.
Лекция 7
Закон
больших чисел
1. Неравенство Маркова
2. Неравенство Чебышёва
3. Теорема Чебышёва
4. Теорема Бернулли
5. Центральная предельная теорема
6. Теорема Ляпунова

2.

Пролог
При некоторых сравнительно широких условиях
суммарное поведение достаточно большого количества
случайных величин почти утрачивает случайный
характер и становится закономерным.
Знание условий, при выполнении которых
совокупное действие случайных причин приводит к
результату, почти не зависящему от случая, позволяет
предвидеть ход явлений.
Эти условия и указываются в теоремах, которые
носят общее название закона больших чисел.
Лекция 7. Закон больших чисел
2

3.

§1. Неравенство Маркова
Теорема 1.
Если случайная величина X принимает
только неотрицательные значения и имеет
математическое ожидание M(X), то для любого
положительного числа А верно неравенство:
M Х
P Х A
.
A
Условие:
Х - случайная величина;
х 0;
(1)
Заключение:
M Х
P Х A
,
A
М Х - математическое ожидание. где A R, A 0.
Лекция 7. Закон больших чисел
3

4.

Пример 1
Средний вес клубня картофеля равен 120 г. Какова
вероятность того, что взятый наугад клубень картофеля
весит не более 360 г?
Эксперимент: выбрать наугад клубень картофеля.
Величина Х: вес выбранного клубня картофеля.
х 0;
М Х =120 г. - средний вес клубня картофеля
(математическое ожидание случайной величины).
Событие Х 360 : клубень весит не более 360 г.
Лекция 7. Закон больших чисел
4

5.

Пример 1
Заключение:
Условие:
Х - случайная величина;
х 0;
M Х
P Х A
,
A
М Х - математическое ожидание. где A R, A 0.
M X
P Х А 1
A
120
P Х 360 1
360
2
P Х 360
3
Лекция 7. Закон больших чисел
5

6.

§1. Неравенство Маркова
Марков
Андрей Андреевич
(1856-1922)
А. А. Марков является
первооткрывателем
обширного класса
стохастических процессов с
дискретной и непрерывной
временной компонентой,
названных марковские
процессы. Он существенно
продвинул классические
исследования касающиеся
закона больших чисел и
центральной предельной
теоремы теории
вероятностей.
Лекция 7. Закон больших чисел
5

7.

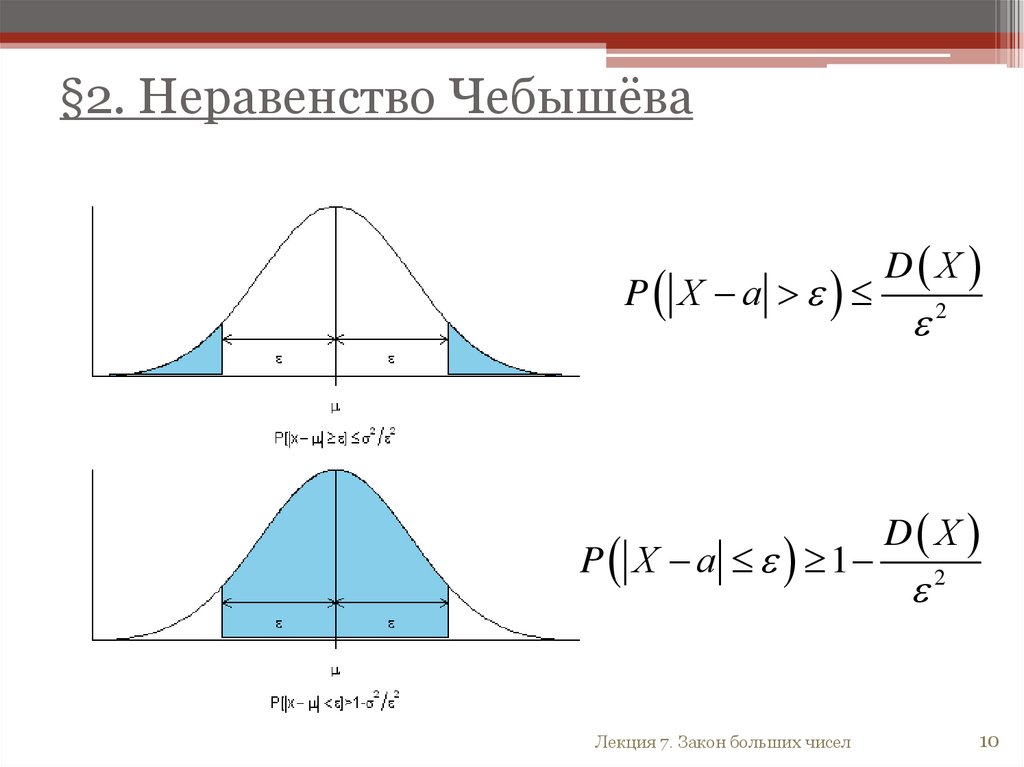
§2. Неравенство Чебышёва
Теорема 2.
Если
случайная
величина
X
имеет
математическое ожидание M(X)=a и дисперсию
D(X), то для любого положительного числа ε
верно неравенство:
P Х а
Условие:
Х - случайная величина;
М Х - матем. ожидание;
D X - дисперсия.
D Х
2
.
(2)
Заключение:
P X M X
где R, 0.
Лекция 7. Закон больших чисел
D X
2
,
7

8.

Пример 2
Всхожесть семян некоторой культуры составляет
75%. Оцените вероятность того, что из посеянных 1000
семян число взошедших окажется в диапазоне от 700 до
800 включительно.
Эксперимент: посадить 1000 семян.
Величина Х: число взошедших семян –
биномиальное распределение, p=0,75, n=1000.
имеет
М Х =np 1000 0, 75 750 - математическое ожидание;
D Х =npq 1000 0, 75 0, 25 187,5 - д исперсия.
Событие 700 Х 800 Х 750 50 : количество
взошедших семян окажется в диапазоне от 700 до 800.
Лекция 7. Закон больших чисел
8

9.

Пример 2
Условие:
Х - случайная величина;
М Х - матем. ожидание;
D X - дисперсия.
Заключение:
P X M X
D X
где R, 0.
P X M X 1
2
,
D X
2
187,5
P X 750 50 1
502
P X 750 50 0,925
Лекция 7. Закон больших чисел
9

10.

§2. Неравенство Чебышёва
P Х а
P Х а 1
Лекция 7. Закон больших чисел
D Х
2
D Х
2
10

11.

§2. Неравенство Чебышёва
Теорема 2.1.
Если случайная величина X=m имеет
биномиальное распределение, то неравенство
Чебышёва принимает вид:
P m np
npq
2
.
(2.1)
Теорема 2.2.
Если случайная величина X=m имеет
биномиальное распределение, то для частости
события
X=m/n
неравенство
Чебышёва
принимает вид:
т
pq
P p 2 .
n
n
(2.2)
Лекция 7. Закон больших чисел
11

12.

§2. Неравенство Чебышёва
Чебышёв
Пафнутий Львович
(1821-1894)
П.Л. Чебышёв стал первым
русским математиком
мирового уровня в теории
вероятностей.
В статье «О средних
величинах» (1866) Чебышёв
доказал и успешно применил
«неравенство Чебышёва»
для решения важной
проблемы — обоснования
закона больших чисел. Здесь
же было введено
общепринятое сегодня
понятие случайной величины.
Лекция 7. Закон больших чисел
5

13.

§3. Теорема Чебышёва
Теорема 3.
Если дисперсии n независимых случайных
величин X1, X2, …, Xn ограничены одной и той
же постоянной C, то при неограниченном
увеличении числа n средняя арифметическая
случайных величин сходится по вероятности к
средней арифметической их математических
ожиданий a1, a2, …, an, т.е.
X 1 X 2 ... X n a1 a2 ... an
lim P
1. (3)
n
n
n
Лекция 7. Закон больших чисел
13

14.

§3. Теорема Чебышёва
Замечание.
Подчеркнём смысл теоремы Чебышёва. При
большом числе n независимых случайных величин X1,
X2, …, Xn практически достоверно, что их средняя
(X1+X2+…+Xn)/n – случайная величина, сколь угодно
мало
отличается
от
неслучайной
величины
(a1+a2+…+an)/n.
Аналитическая
запись
утверждения
теоремы
Чебышёва более удобная для решения задач имеет вид:
X 1 X 2 ... X n a1 a2 ... an
С
P
1 2 . (3.1)
n
n
n
Лекция 7. Закон больших чисел
14

15.

§3. Теорема Чебышёва
Условие:
Х 1 , Х 2 , ..., Х n - независимые случайные величины;
a1 , a2 , ..., an - математические ожидания;
D1 , D2 , ..., Dn - дисперсии;
С const : D1 С, D2 С, ..., Dn С.
Заключение:
X 1 X 2 ... X n a1 a2 ... an
С
P
1 2 ,
n
n
n
где R, 0.
Лекция 7. Закон больших чисел
15

16.

§3. Теорема Чебышёва
Следствие.
Если дисперсии n независимых случайных величин
X1, X2, …, Xn ограничены одной и той же постоянной C,
а математические ожидания равны а, то теорема
Чебышёва принимает вид:
X 1 X 2 ... X n
С
P
а 1 2 .
n
n
Лекция 7. Закон больших чисел
(3.2)
16

17.

Пример 3
Определите, сколько надо произвести замеров
поперечного сечения деревьев, чтобы средний диаметр
деревьев отличался от истинного значения а не более
чем на 2 см с вероятностью не меньшей 95%, если
среднее квадратичное отклонение поперечного сечения
деревьев не превышает 10 см и измерения проводятся
без погрешности.
Эксперимент: измерить диаметр поперечного сечения
наугад выбранного дерева; n – число замеров (деревьев)
Величина Хi: диаметр поперечного сечения дерева при
i-ом измерении; σ(Хi)<10; i = 1, 2, …, n.
Событие X 1 X 2 ... X n / n а 2
:
средний
диаметр при n измерениях отличается от истинного
17
значения a не более чем на 2 см. Лекция 7. Закон больших чисел

18.

Пример 3
Условие:
Х 1 , Х 2 , ..., Х n - независимые случайные величины;
a1 a2 ... an a - математическое ожидание;
1 , 2 , ..., n - средние квадратичные отклонения;
С const : 1 С, 2 С, ..., n С
D1 С2 , D2 С2 , ..., Dn С2 .
Заключение:
X 1 X 2 ... X n
С2
P
а 1 2 ,
n
n
где R, 0.
Лекция 7. Закон больших чисел
18

19.

Пример 3
X 1 X 2 ... X n
102
P
а 2 1
2
n
n
2
Вероятность события
меньше чем 95%.
X X ... X / n а 2 не
1
2
n
102
1
0,95
2
n 2
100
25
0, 05; n
; n 500
n 4
0, 05
Лекция 7. Закон больших чисел
19

20.

§4. Теорема Бернулли
Теорема 4.
Частость
события
в
n
повторных
независимых испытаниях, в каждом из которых
оно может произойти с одной и той же
вероятностью
p,
при
неограниченном
увеличении числа n сходится по вероятности к
вероятности p
этого события в отдельном
испытании:
m
lim P p 1.
n
n
(4)
Утверждение является частным случаем теоремы
Чебышёва и непосредственно вытекает из неравенства
Чебышёва (стр.11, §2, Терема 2.2).
Лекция 7. Закон больших чисел
20

21.

§4. Теорема Бернулли
Условие:
Серия повторных испытаний;
n - количество испытаний;
А - событие, наступающее в результате испытания;
р - вероятность наступления события в каждом испытании;
m
- частость события.
n
Заключение:
m
pq
P p 1 2 ,
n
n
где R, 0.
Лекция 7. Закон больших чисел
21

22.

§4. Теорема Бернулли
Замечание.
Подчеркнём смысл теоремы Чебышёва. При
большом числе n повторных независимых испытаний
практически
достоверно,
что
частость
или
статистическая вероятность события m/n – случайная
величина, сколь угодно мало отличается от
неслучайной величины p – вероятности события, т.е.
практически перестаёт быть случайной.
Теорем Бернулли даёт теоретическое обоснование
замены неизвестной вероятности события его
частостью, полученной в повторных независимых
испытаниях, проводимых при неизменном комплексе
условий.
Лекция 7. Закон больших чисел
22

23.

Пример 4
При штамповке пластинок из пластмассы брак
составляет 3%. Найдите вероятность того, что при
проверке партии в 1000 пластинок выявится
отклонение от установленного процента брака меньше
чем на 1%.
Эксперимент: выбрать наугад пластинку для проверки
качества; n=1000 – число проверок (пластинок).
Событие
А:
выбрана
бракованная
пластинка,
p=P(A)=0,03.
Событие m / n 0, 03 0, 01 :
частость
выбора
бракованных пластинок отклоняется от установленного
процента брака меньше чем на 1%.
Лекция 7. Закон больших чисел
23

24.

Пример 4
Условие:
Серия повторных испытаний;
n - количество испытаний;
А - событие, наступающее в результате испытания;
р - вероятность наступления события в каждом испытании;
m
- частость события.
n
Заключение:
m
0, 03 0,97
P 0, 03 0, 01 1
2
n
1000
0,
01
m
P 0, 03 0, 01 0, 709
n
m
pq
P p 1 2 ,
n
n
где R, 0.
Лекция 7. Закон больших чисел
24

25.

§4. Теорема Бернулли
Теорема 5 (Пуассона).
Частость
события
в
n
повторных
независимых испытаниях, в каждом из которых
оно
может
произойти
соответственно
с
вероятностями p1, p2, …, pn, при неограниченном
увеличении числа n сходится по вероятности к
средней арифметической вероятностей события
в отдельных испытаниях, т.е.
m p1 p2
lim P
n
n
n
pn
1.
Утверждение
является
обобщением
Бернулли и следует из теоремы Чебышёва.
(5)
теоремы
Лекция 7. Закон больших чисел
25

26.

§5. Центральная предельная теорема
Рассмотренные
выше
формулировки
закона
больших чисел устанавливают факт приближения
средней большого числа случайных величин к
определённым постоянным.
Оказывается, что этим закономерности суммарного
действия случайных величин не исчерпываются. При
некоторых достаточно общих условиях совокупное
действие большого числа случайных величин приводит
к нормальному закону распределения.
Группа теорем, посвященных описанию условий
возникновения случайной величины, подчиняющейся
нормальному закону распределения, называется
центральной предельной теоремой. Важнейшее
место среди них занимает теорема Ляпунова.
Лекция 7. Закон больших чисел
26

27.

§6. Теорема Ляпунова
Теорема 6.
Если X1, X2, …, Xn – независимые случайные
величины, имеющие математические ожидания
M(Xi)=ai, дисперсии D(Xi)=σi2, абсолютные
центральные моменты третьего порядка
M(|Xi-ai|3)=mi и при этом выполняется условие
n
m
lim
n
i 1
i
n 2
i
i 1
3/ 2
0,
Лекция 7. Закон больших чисел
(6)
27

28.

§6. Теорема Ляпунова
то закон распределения суммы случайных
величин Y=X1+X2+…+Xn при n
неограниченно приближается к нормальному
с математическим ожиданием M Y
и дисперсией D Y
n
.
i 1
2
i
n
a
i 1
i
Замечание.
Условие
(6)
в
формулировке
центральной
предельной теоремы называют условием Ляпунова.
Лекция 7. Закон больших чисел
28

29.

§6. Теорема Ляпунова
Условие:
Х 1 , Х 2 , ..., Х n - независимые случайные величины;
a1 , a2 , ..., an - математические ожидания;
21 , 2 2 , ..., 2 n - дисперсии;
M X i ai
3
m - абсолютные центральные моменты третьего порядка,
i
n
m
lim
n
i 1
i
n 2
i
i 1
3
2
0 - условие Ляпунова.
Заключение:
Y X 1 X 2 ... X n - нормально распределенная случайная величина;
n
M Y ai - математическое ожидание;
i 1
n
D Y i2 - дисперсия.
i 1
Лекция 7. Закон больших чисел
29

30.

§6. Теорема Ляпунова
Следствие.
Если X1, X2, …, Xn – независимые случайные
величины, имеющие одинаковое математическое
ожидание M(Xi)=a, дисперсию D(Xi)=σ2 и абсолютный
центральный момент третьего порядка M(|Xi-a|3)=m, то
закон распределения суммы случайных величин
Y=X1+X2+…+Xn при n неограниченно
приближается к нормальному.
В частности, если все случайные величины Xi
одинаково распределены, то закон распределения их
суммы неограниченно приближается к нормальному
при n .
Лекция 7. Закон больших чисел
30

31.

§6. Теорема Ляпунова
Ляпунов
Александр Михайлович
(1857-1918)
Важнейшее достижение
А.М.Ляпунова – теория
устойчивости равновесия и
движения механических
систем. В теории
вероятностей он предложил
новый метод исследования
(метод «характеристических
функций»); доказал так
называемую центральную
предельную теорему при
значительно более общих
условиях, чем его
предшественники.
Лекция 7. Закон больших чисел
31

32.

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Теория вероятностей и математическая статистика
лектор Макеева О.В.
Продолжение следует…