Похожие презентации:
Закон больших чисел и центральная предельная теорема
1.
Глава 5. Закон большихчисел и центральная
предельная теорема
2.
Предельные теоремы можно разделить надва типа.
1. Теоремы, которые устанавливают, что
среднее значение достаточно большого
числа СВ обладает достаточной
устойчивостью и может быть предсказано
с высокой степенью точности.
2. Теоремы, в которых устанавливается,
что поведение средних величин в
пределе может быть оценено законом
распределения, близким к нормальному.
3.
§5.1. Последовательностислучайных величин и их
сходимость
4.
Пусть на вероятностном пространстве ( , F, P)определены случайные величины
Y (Y1, Y2,…, Yn) со значениями
Y( ) (Y1( ), Y2( ),…, Yn( )).
1. Говорят, что последовательность Yn сходится
по вероятности (п.в.) к Y, если
0:
( Yn -Y )=0 - (Ynп.в. Y )
2. Говорят, что последовательность Yn сходится к
Y почти наверное (п.н.) (с вероятностью 1,
почти всегда, почти
всюду на , mod P), если
P( A) 1
.
5.
Здесь A = { : nlimYn( )=Y( )}
п.н. Y )
(
Y
Обозначим эту сходимость в виде n
3. Говорят, что последовательность Yn
сходится к Y в среднем квадратическом
(с.к.), если
lim M[(Y – Y2)]=0
n
n
Сходимость Yn к Y в среднем
квадратическом обозначают Y= nlim
Yn
c.к.
или (Yn
Y)
6.
4. Говорят, что последовательность Ynсходится к Y по распределению (п.р.),
lim
(Ynп. р. Y ) , если
n Fn(y)=F(y).
Здесь Fn, F – функции распределения Yn и
Y , причем сходимость (Fn) к F
подразумевается для всех y, за
исключением, может быть, точек
разрыва F.
7.
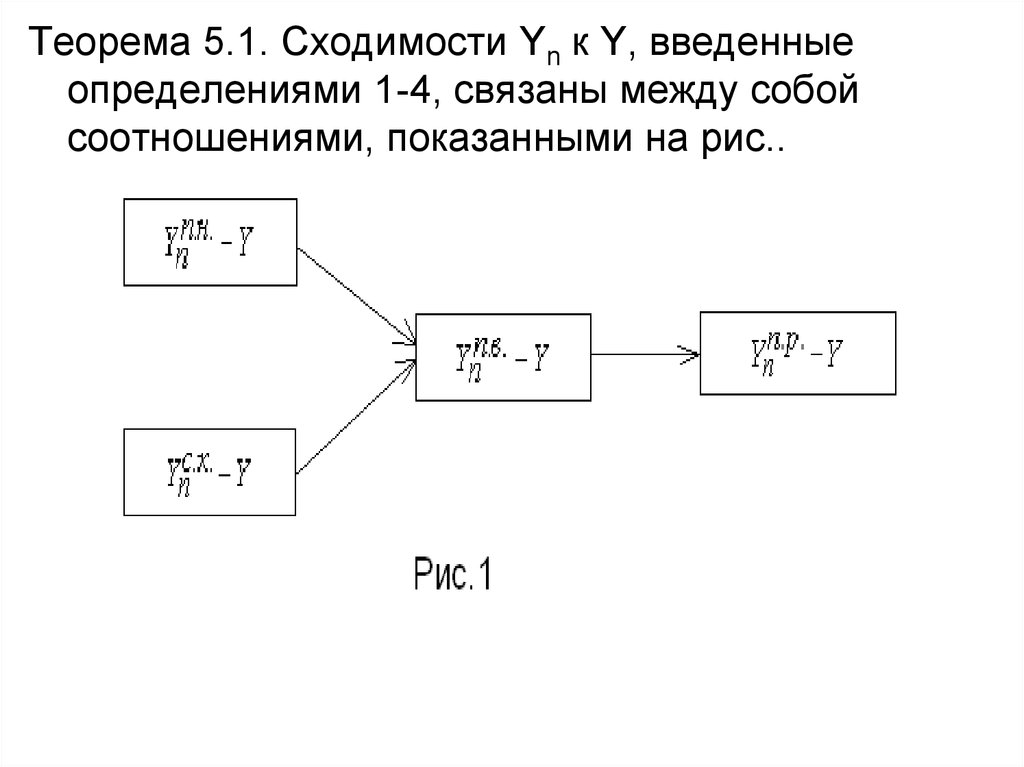
Теорема 5.1. Сходимости Yn к Y, введенныеопределениями 1-4, связаны между собой
соотношениями, показанными на рис..
(Ynп. р. Y )
8.
п.
р
.
Теорема 5.2. (Yn Y ) [P(Y=C)=1] (Ynп.в. Y ) .
Следующая теорема решает вопрос о сходимости
последовательности значений функции,
соответствующих элементам сходящейся
вероятности последовательности СВ-н. Эта
теорема, в частности, имеет важное применение
в математической статистике.
Теорема 5.3. Если g – непрерывная функция и
(Ynп.в. Y ) , то g (Y )п.в. g (Y ) .
n
.
9.
Эта теорема справедлива и в случае, когдаg представляет собой непрерывную
функцию более чем одного аргумента.
Например, если g - непрерывная функция
двух аргументов, то
( X nп.в. X ) (Ynп.в. Y )
g ( X , Y )п.в. g ( X , Y )
n n
10.
Теорема 5.4. Пусть последовательность{Хn} сходится по распределению к
случайной величине Х с функцией
распределения F(x) и последовательность
{Yn} сходится по вероятности к постоянной
величине 0. Тогда последовательность
{Zn}, где Zn =Xn/Yn, сходится по
распределению к СВ Z с функцией
распределения P(Z<z)=F( z).
11. §5.2.Неравенство Чебышева
СВ Х с МО M[X]=mx< и дисперсиейD[Х]=Dx< .
Вероятность того, что отклонение СВ
Х от ее МО mx по абсолютной величине
больше числа , ограничена сверху
величиной Dx/ 2, т.е.
P{ X-mx }<Dx/ 2 или
P{ X-mx < } 1 - Dx/ 2.
12.
Доказательство: P{ X-mx }=pi
xi mx
2
n
n
2
2
2
x
m
p
x
m
p
(
x
m
)
p
Dx= i
i
i
x i
i = i 1 i
i 1
x m
i
x
x m
i x
p 2 P{ X m }
i
x
13. §5.3. Теорема Чебышева
Теорема: При достаточно большом числеопытов n среднее арифметическое x
значений х1, …, хn СВ Х сходится по
P{ x m } 1
вероятности к ее МО mx, т.е. nlim
x
1 n
x xi
n i 1
Доказательство: х1, …, хn – независимы, M[Xi]=mx ;
D[Xi]=Dx
1 n
Хi
Y=
n i 1
14.
11 n 1 n 1 n
m y M [ Y ] M X i M X i M [ X i ] nmx m x
n i 1 n i 1 n i 1
n
Dy
1 n
D[Y ] D X i 1
n
2
i 1
n
n
n
1
1 nD
D X i
D
[
X
]
x
i
2
2
n
i 1
n i 1
Т.к. my=mx< , Dy=1/nDx< . то
lim P{ Y m } 1
x.
n
1 n
lim P X m 1
x
n n i 1 i
1
Dx
n
15.
Обобщенная теорема Чебышева.Пусть Х1, …, Хn – последовательность
независимых случайных величин с mxi< и
Dxi< L, i = 1, …, n, тогда при неограниченном
увеличении n
1 n
lim P X
ni 1 i
n
1 n
mx
ni 1 i
1
1 n
Доказательство: Пусть Y= Х i . Тогда
n i 1
1 n
1 n 1 n 1 n
m y M [ Y ] M X i M X i M [ X i ] mx
n i 1 n i 1 n i 1
n i 1 i
16.
Dy1
1 n 1 n 1 n
D[ Y ] D
n i 1 X i 2 D i 1 X i 2 i 1 D [ X i ] 2 nL
n
n
n
Применим неравенство Чебышева:
P{ Y m
y
} 1
1
n 2
D
y
1 n
1 n
1
P
L
X i mx 1
ni 1
ni 1
2
i
n
Отсюда следует справедливость теоремы:
1 n
lim P
Xi
ni 1
n
1 n
mx
ni 1
i
1
17. §5.4. Центральная предельная теорема
18.
Теорема Ляпунова. Если случайныевеличины в последовательности X1,
X2,...,Xn,... независимы, одинаково
распределены и имеют конечное
математическое ожидание mx и
дисперсию
, то для любого
действительного x
,
19.
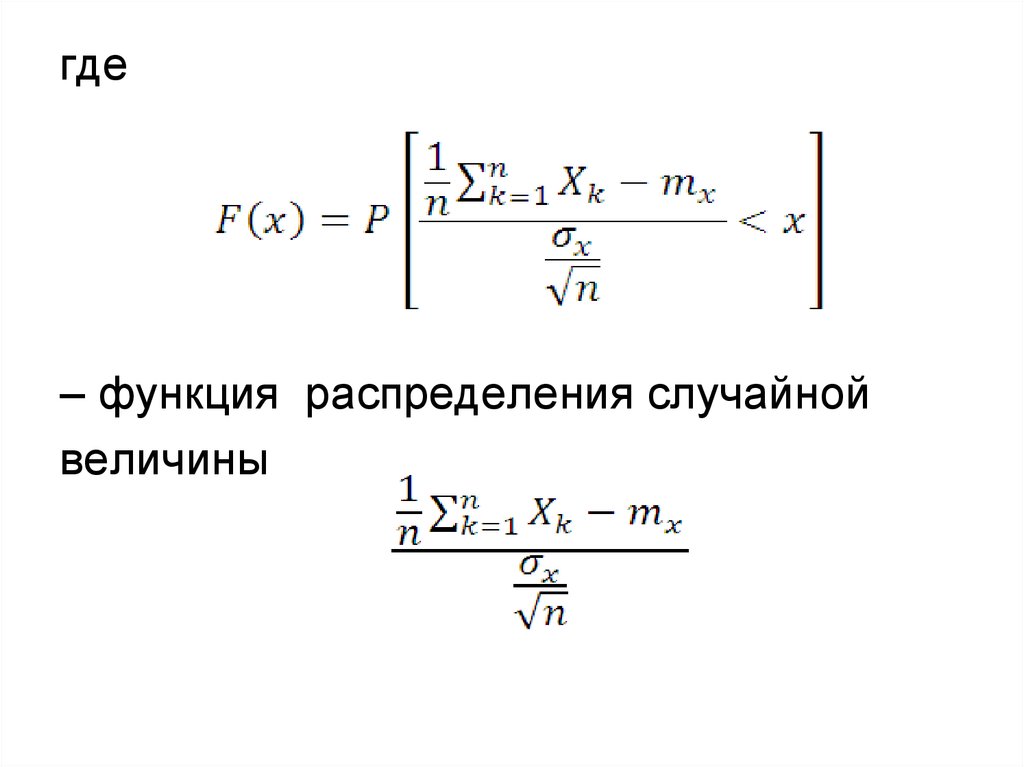
где– функция распределения случайной
величины
20. §5.5. Теорема Бернулли
21.
Теорема Бернулли. При неограниченном численезависимых опытов n частота появления
события А: р*=m/n (m – число появления события
А) сходится по вероятности к его вероятности р:
lim P р * р 1
n
Доказательство: Пусть Хi – дискретная случайная
величина с M[X]=mxi и D[Х]=Dxi характеризующая
появление события А в i-м опыте, закон
распределения которой определяется рядом
22.
Хi0
1
P(Xi)
1 – pi = qi
pi
где Хi =0 означает, что событие А не
произошло, а Хi =1 означает, что событие
А произошло.
Определим mxi и Dxi :
23.
mxi =0 q + 1 p = p;Dxi =(0-p)2q+(1-p)2p= p2q+q2p=pq(p+q)=pq<1/4.
Таким образом, математическое ожидание и
дисперсия являются ограниченными
величинами. Так как
,
то по т.Чебышева
или
1 n
lim P X
n n i 1 i
m
x
1
lim P р * р 1
n
24.
Теорема Бернулли используется дляобоснования замены вероятностей
событий частотой их появления. Теорема
Бернулли не позволяет утверждать, что
неравенство
m
n
p
будет выполняться для достаточно
больших чисел n. Она лишь утверждает,
что выполнение такого неравенства при
достаточно большом числе n будет очень
вероятным.
25.
Теорема Бернулли утверждаетустойчивость частоты при постоянных
условиях опыта.
26.
§5.6. Теорема ПуассонаПри переменных условиях опыта
свойства
устойчивости
частоты
доказывается теоремой Пуассона.
27.
Теорема: При неограниченном численезависимых опытов n частота
появления события А сходится по
вероятности к среднему арифметическому
вероятностей pi=P(Ai) появления события
А i-м опыте:
1 n
lim P p * pi
n
n i 1
1
28.
Доказательство: Появления события А вi-м опыте характеризуется законом
распределения, который определяется
рядом:
Хi
0
1
P(Xi)
1 – pi = qi
pi
где Хi =0 означает, что событие А не
произошло, а Хi =1 означает, что событие
А произошло.
29.
Определим mxi и Dxi :mxi = 0 qi+1 pi=pi;
Dxi =(0- pi)2qi+(1-pi)2pi=pi2qi+ qi2pi=piqi(pi+qi)=piqi<1/4.
Т.о., случайная величина Хi удовлетворяет
условиям обобщенной т.Чебышева. Так как
1 n
1 n
и
m pi
n i 1 xi n i 1
то получим:
lim P
n
1 n
1 n
Xi
m xi 1
n i 1
n i 1
30.
или1 n
lim P p * pi
n
n i 1
1
что завершает доказательство.












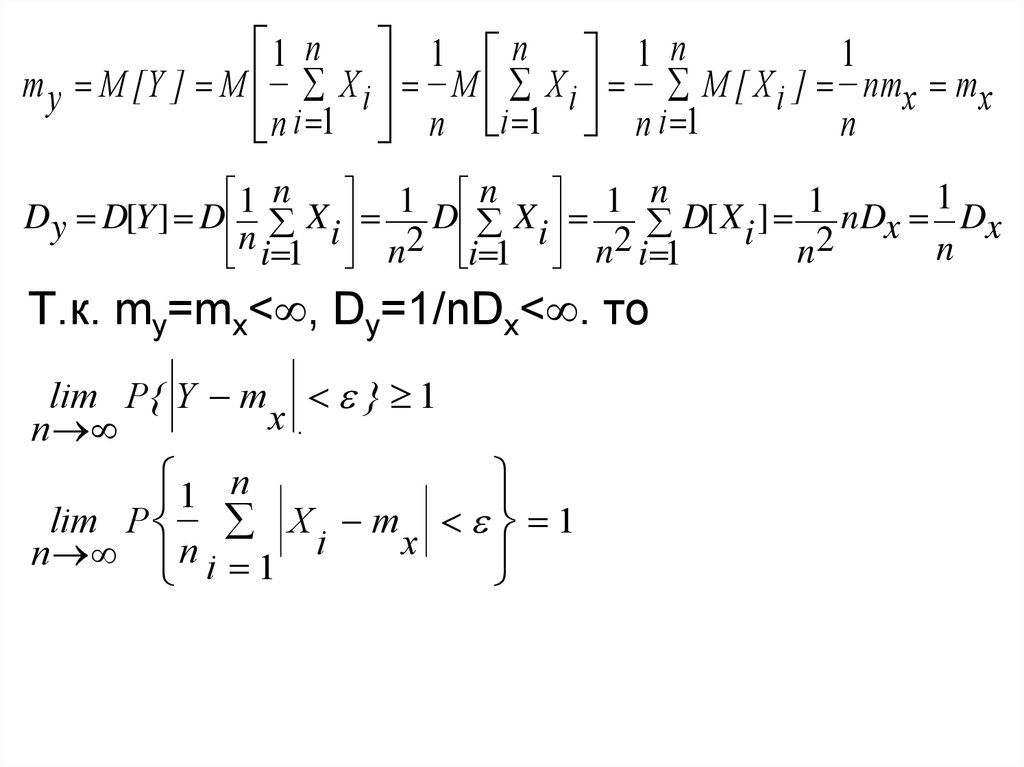















 Математика
Математика








