Механические колебания

1. Механические колебания

ВоГУ
Лекция 07
Механические колебания
Кузина Л.А.,
к.ф.-м.н., доцент
2019 г.
1

2. План

1. Колебательные процессы. Гармонические колебания.
Понятие о спектральном разложении.
2. Дифференциальное уравнение гармонических
колебаний.
3. Пружинный, физический и математический маятники.
4. Энергия гармонического осциллятора.
5. Сложение колебаний.
5.1. Сложение колебаний одинаковой частоты,
происходящих вдоль одной прямой.
5.2. Сложение взаимно перпендикулярных колебаний
одинаковой частоты.
5.3. Сложение взаимно перпендикулярных колебаний
кратных частот. Фигуры Лиссажу.
2

3.

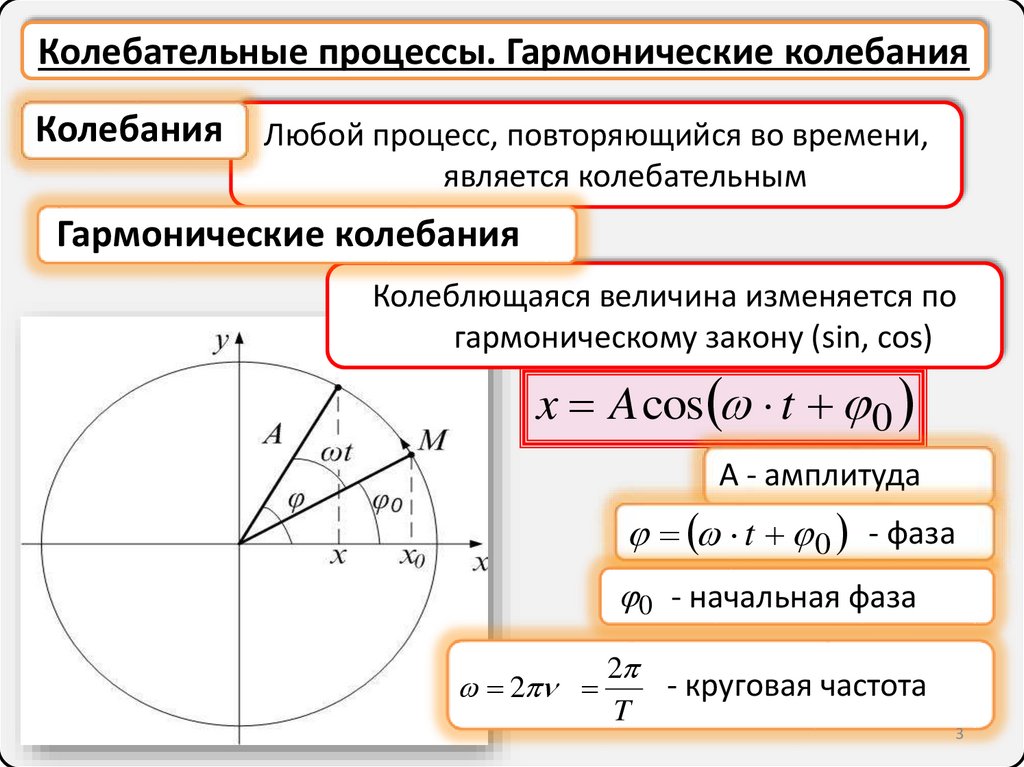
Колебательные процессы. Гармонические колебания
Колебания
Любой процесс, повторяющийся во времени,
является колебательным
Гармонические колебания
Колеблющаяся величина изменяется по
гармоническому закону (sin, cos)
x A cos t 0
А - амплитуда
t 0 - фаза
0 - начальная фаза
2
- круговая частота
2
T
3

4.

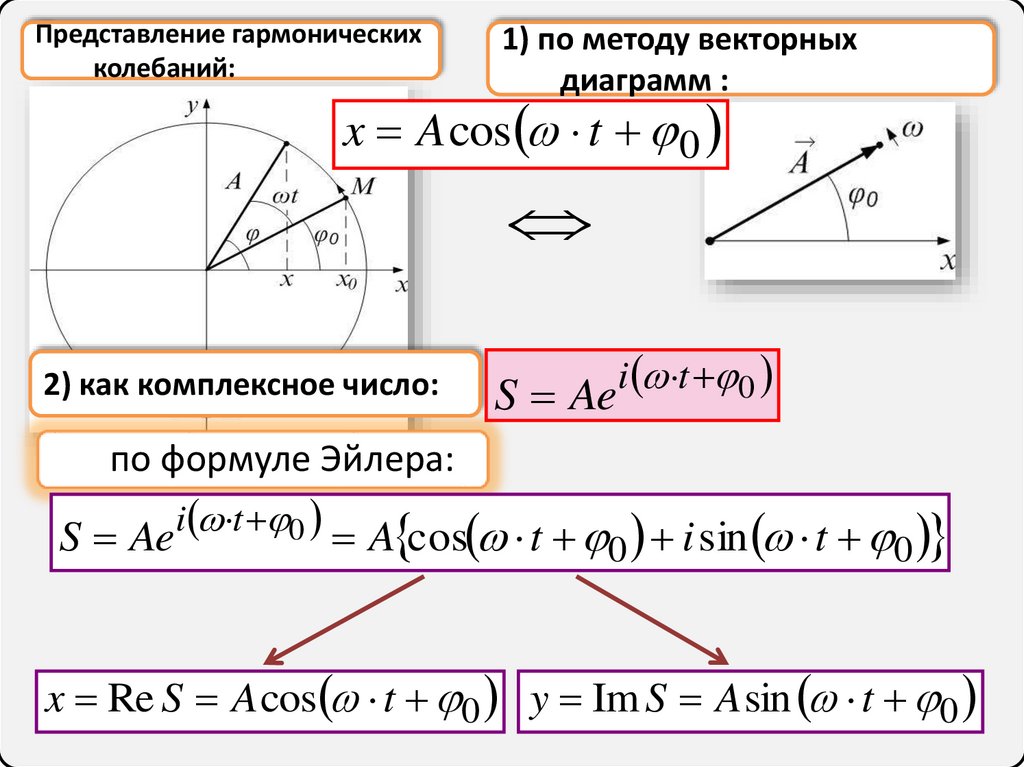
Представление гармонических
колебаний:
1) по методу векторных
диаграмм :
x A cos t 0
2) как комплексное число:
S Aei t 0
по формуле Эйлера:
i t 0
S Ae
A cos t 0 i sin t 0
x Re S A cos t 0 y Im S A sin t 0

5.

Понятие о спектральном разложении. Ряд Фурье
Теорема Фурье:
любую периодическую функцию можно
представить в виде ряда Фурье
(разложить по гармоническим составляющим)
f t f t T
T
2
0
f t a0 an cos n 0t bn sin n 0t
n 1
Для чётной функции:
f t f t
bn 0
f t a0 an cos n 0t
n 1

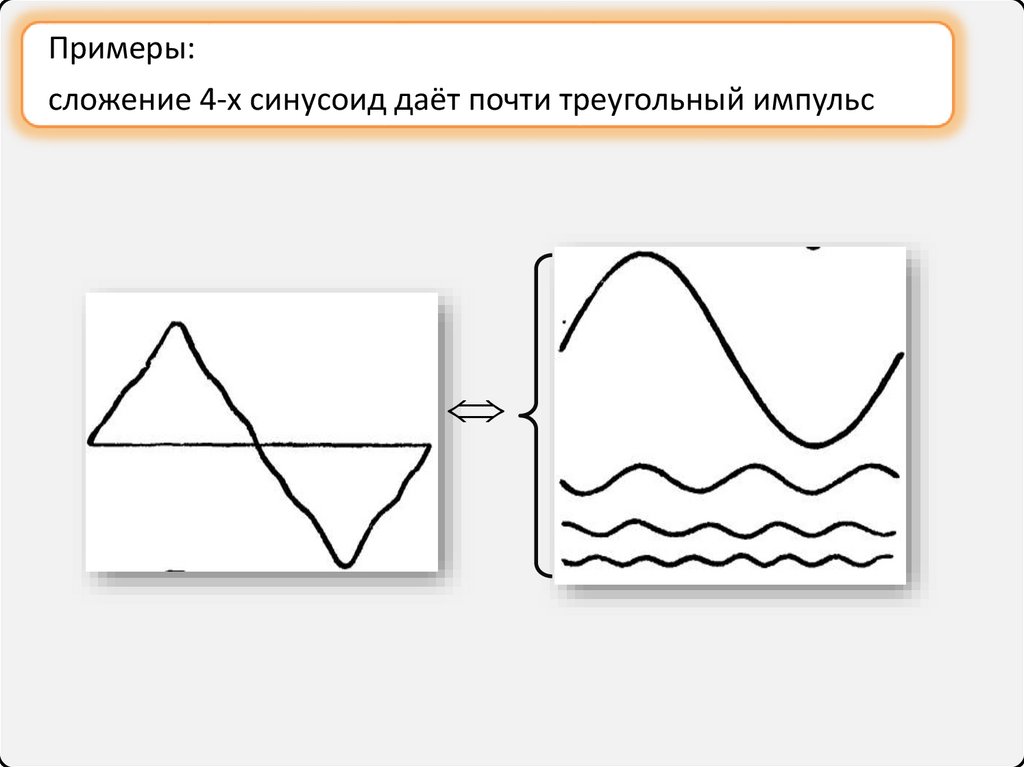
6.

Примеры:
сложение 4-х синусоид даёт почти треугольный импульс

7.

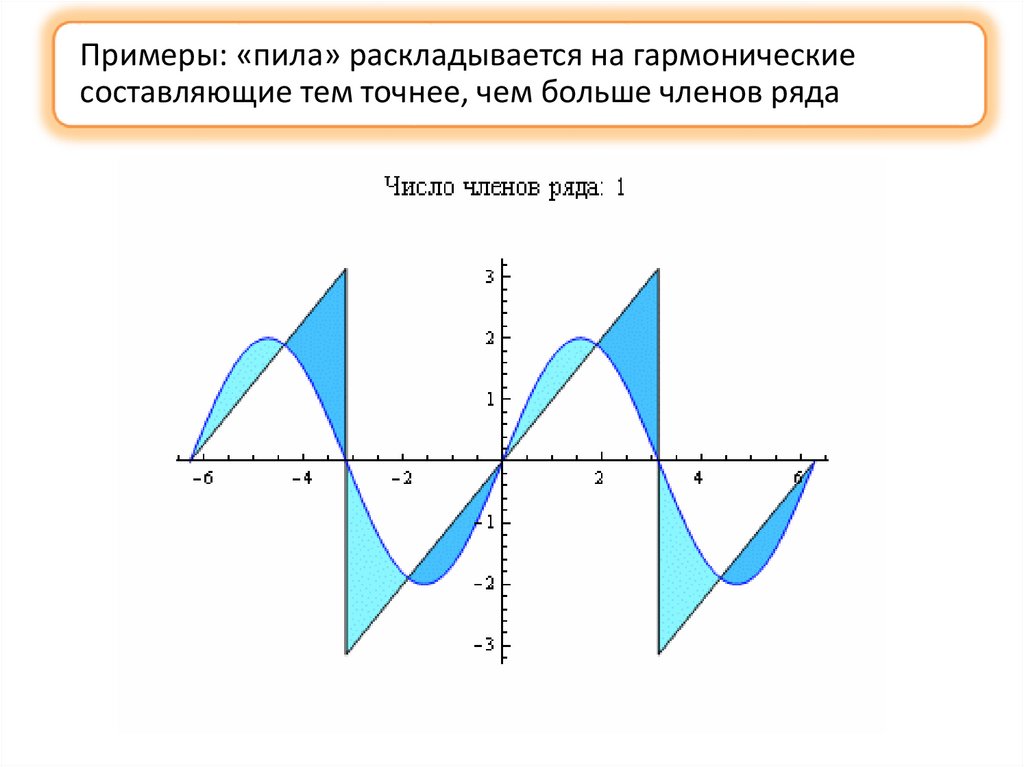
Примеры: «пила» раскладывается на гармонические
составляющие тем точнее, чем больше членов ряда

8.

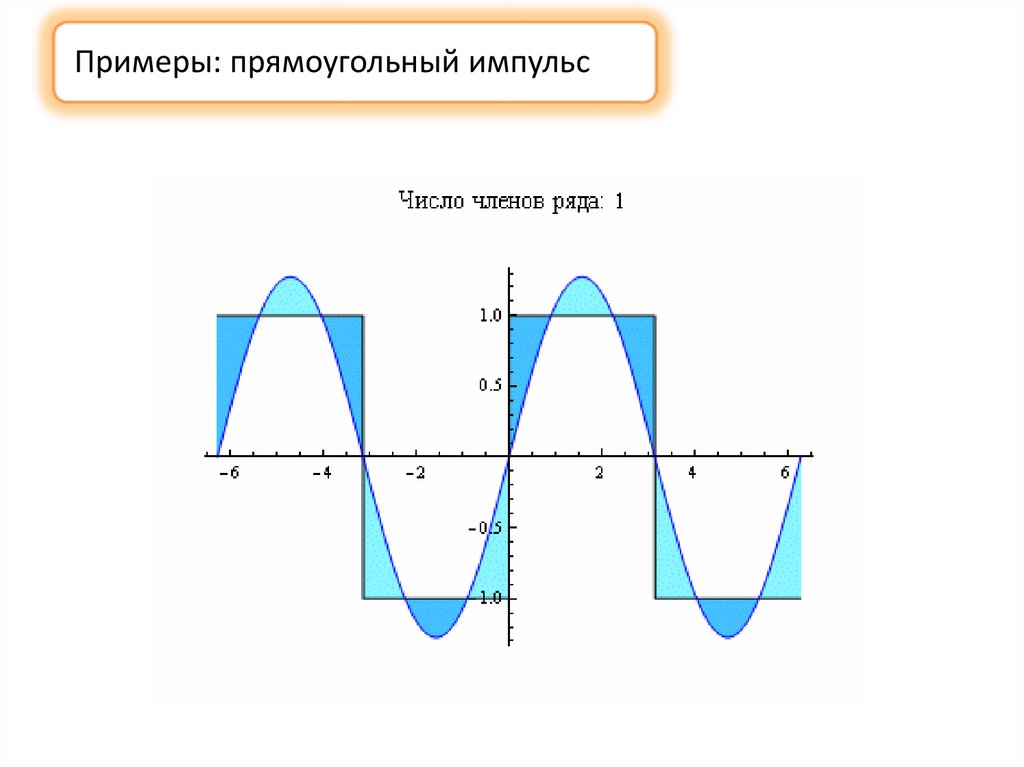
Примеры: прямоугольный импульс

9.

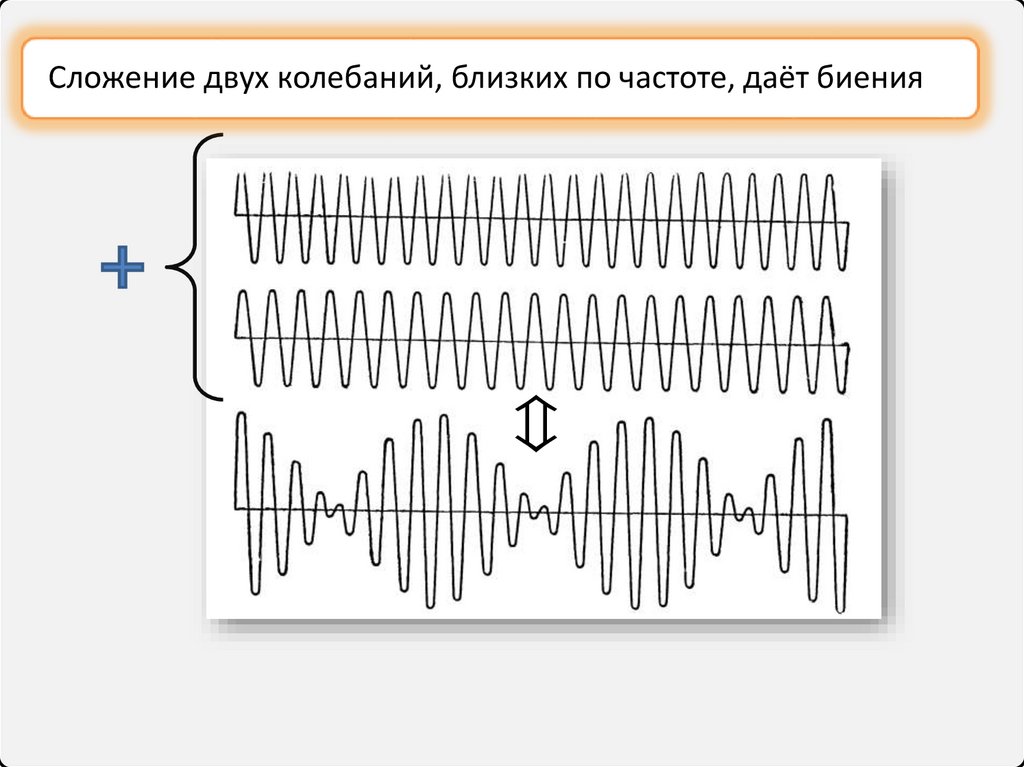
Сложение двух колебаний, близких по частоте, даёт биения

10.

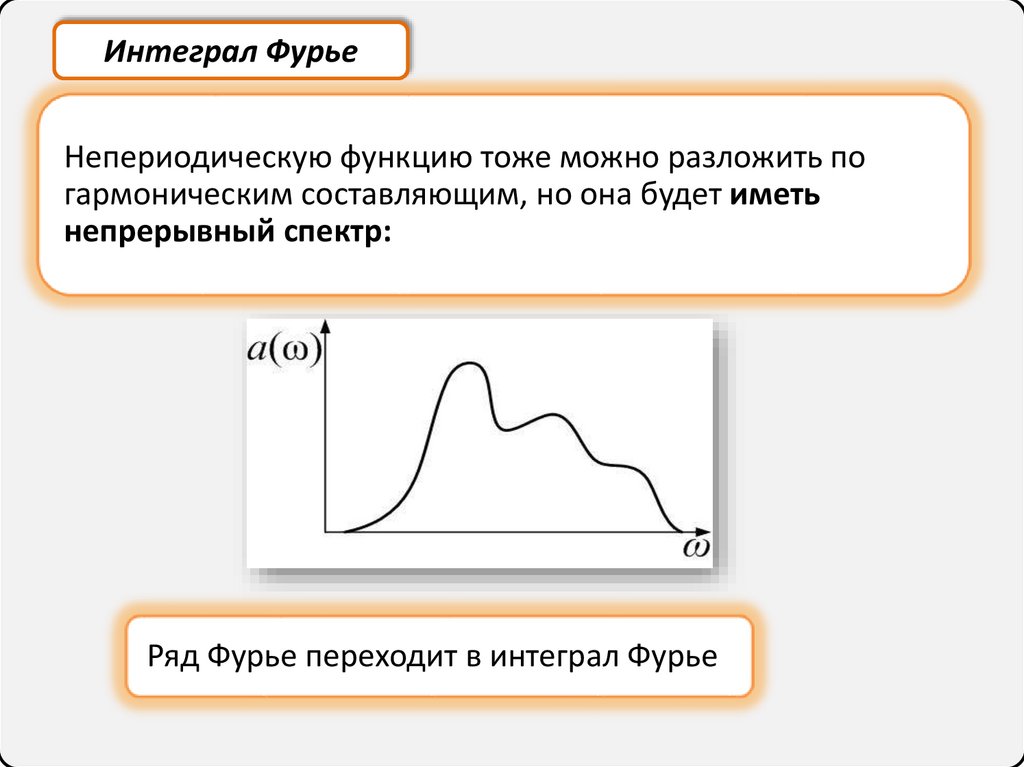
Интеграл Фурье
Непериодическую функцию тоже можно разложить по
гармоническим составляющим, но она будет иметь
непрерывный спектр:
Ряд Фурье переходит в интеграл Фурье

11.

Дифференциальное уравнение гармонических колебаний
x A cos t 0
x A sin t 0
a x 2 A cos t 0 2 x
2
x x 0
Решение этого дифференциального
уравнения – гармоническая функция:
Сила пропорциональна смещению
F ma m 2 x kx
(квазиупругая, возвращающая)
k m 2

12.

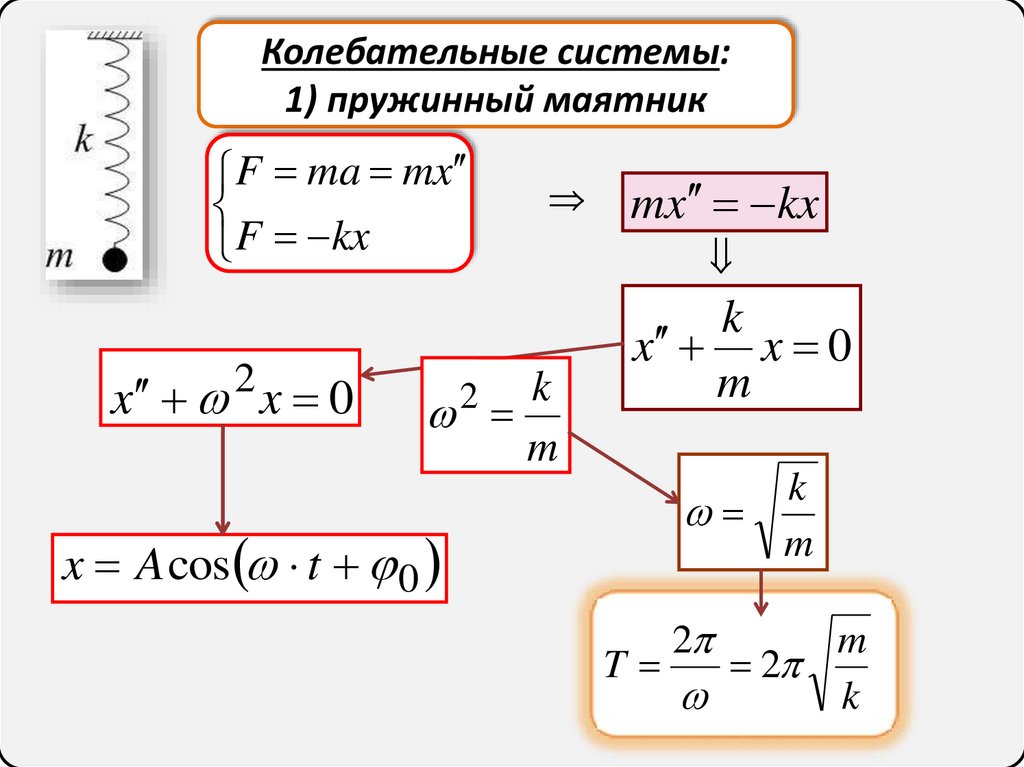
Колебательные системы:
1) пружинный маятник
F ma mx
F kx
x x 0
2
k
m
x A cos t 0
2
mx kx
k
x x 0
m
k
m
2
m
T
2
k

13.

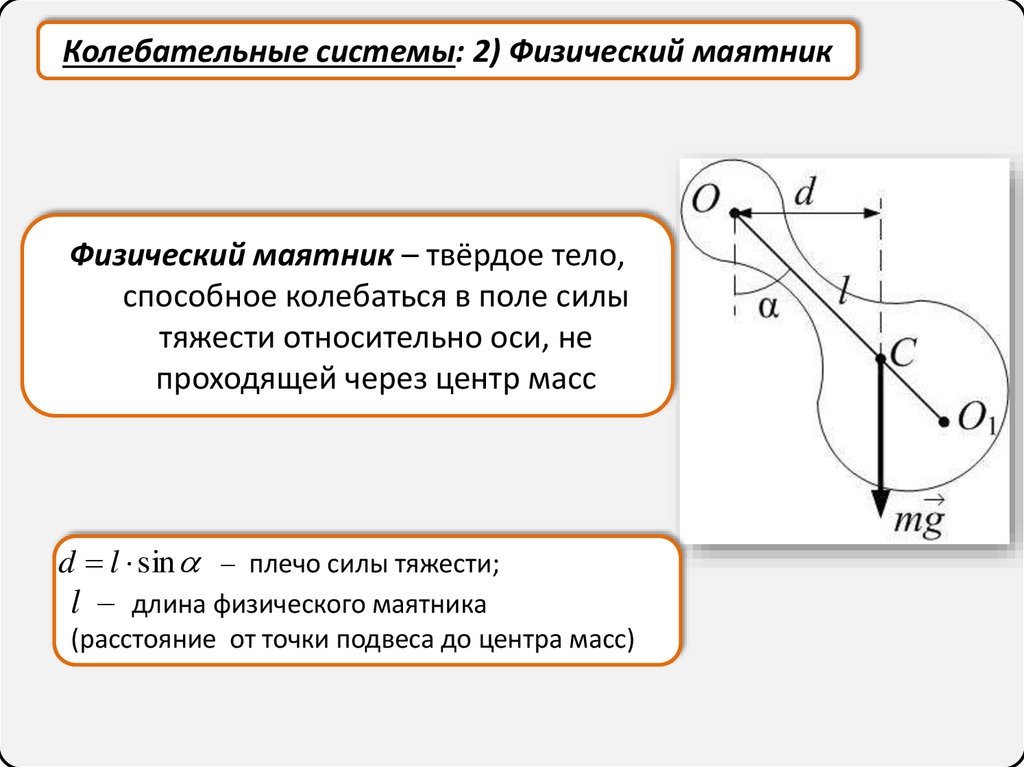
Колебательные системы: 2) Физический маятник
Физический маятник – твёрдое тело,
способное колебаться в поле силы
тяжести относительно оси, не
проходящей через центр масс
d l sin – плечо силы тяжести;
l – длина физического маятника
(расстояние от точки подвеса до центра масс)

14.

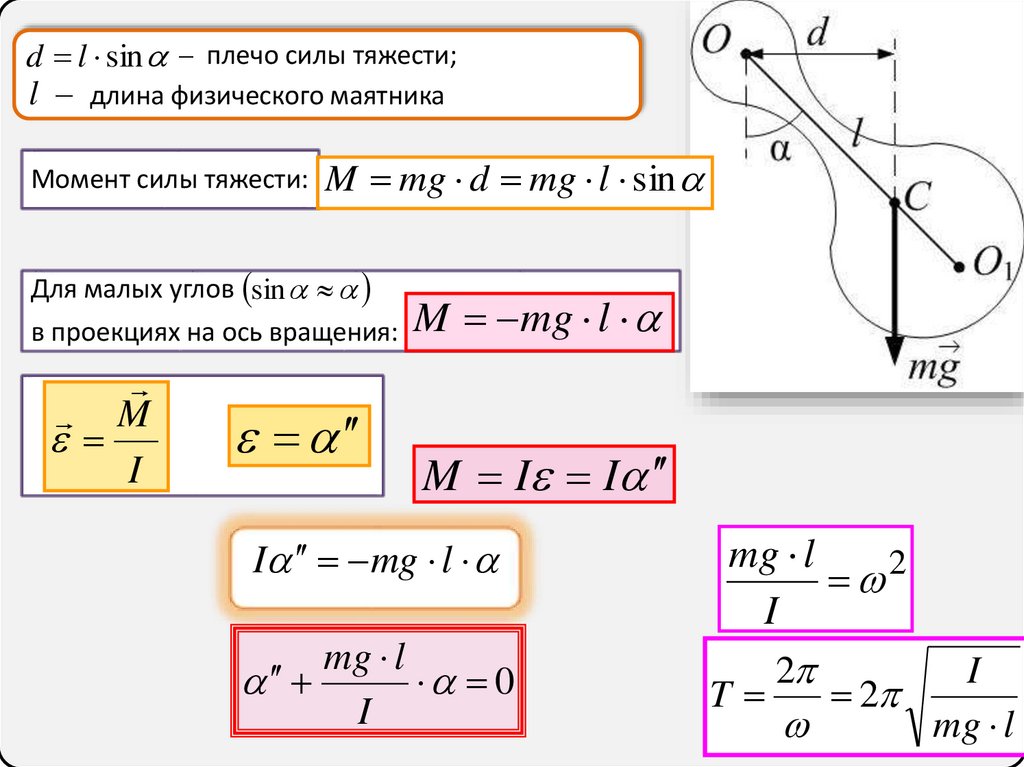
d l sin – плечо силы тяжести;
l – длина физического маятника
Момент силы тяжести: M mg d mg l sin
Для малых углов sin
в проекциях на ось вращения: M mg l
M
I
M I I
I mg l
mg l
0
I
mg l
2
I
2
I
T
2
mg l

15.

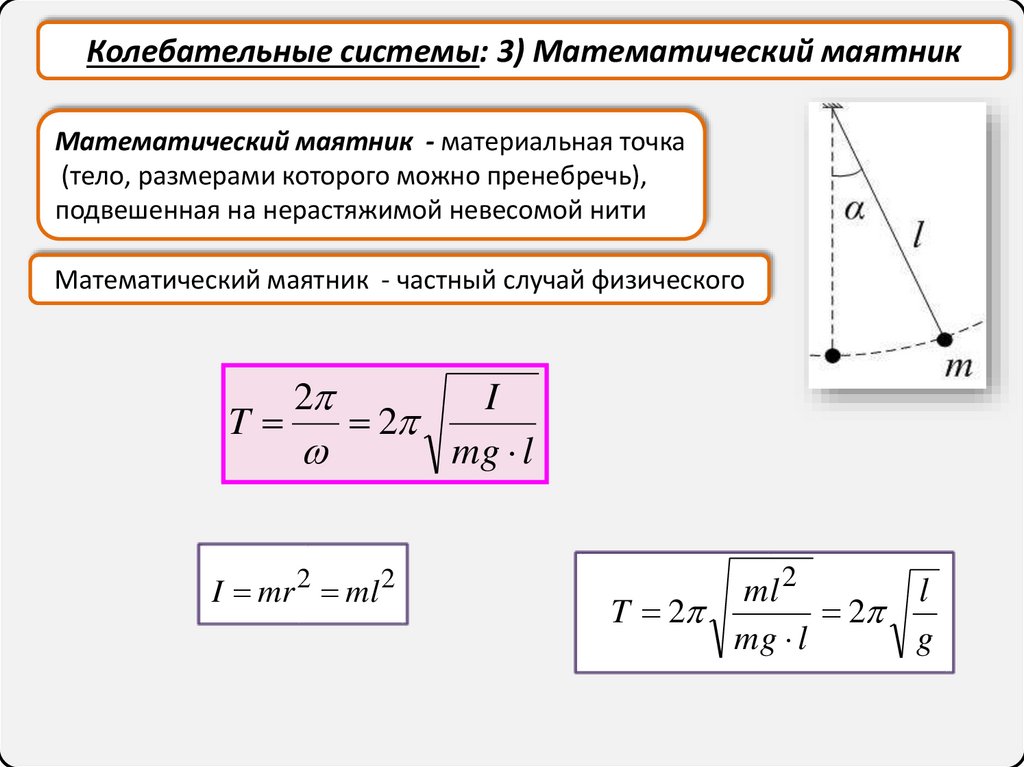
Колебательные системы: 3) Математический маятник
Математический маятник - материальная точка
(тело, размерами которого можно пренебречь),
подвешенная на нерастяжимой невесомой нити
Математический маятник - частный случай физического
2
I
T
2
mg l
I mr 2 ml 2
ml 2
l
T 2
2
mg l
g

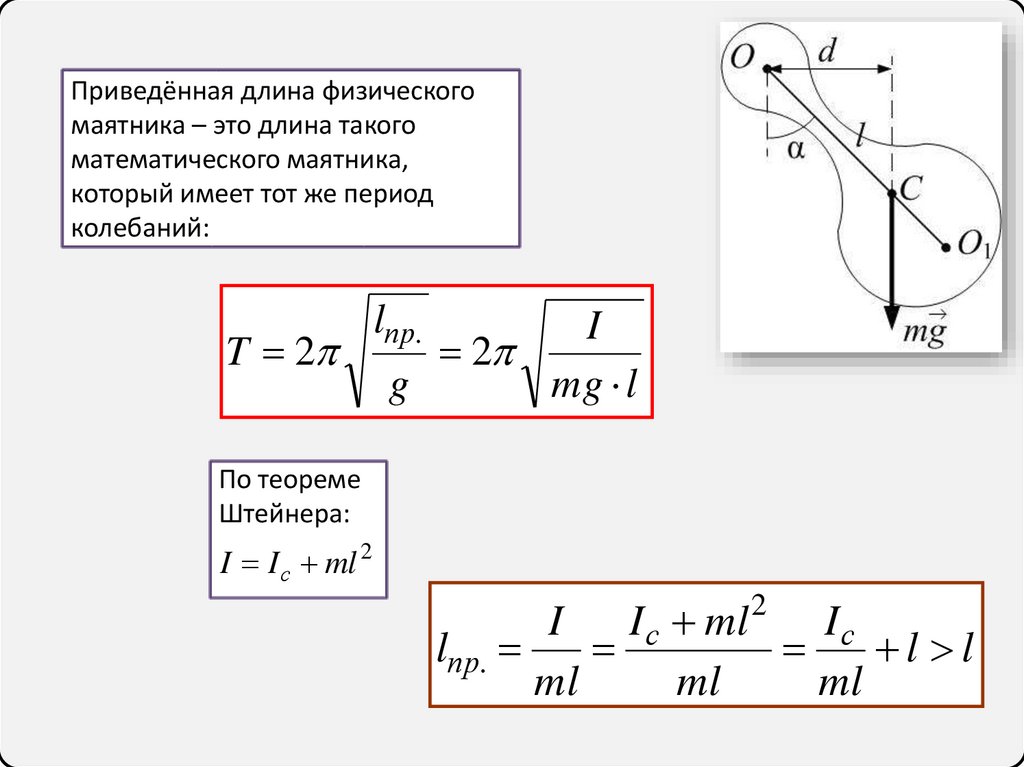
16.

Приведённая длина физического
маятника – это длина такого
математического маятника,
который имеет тот же период
колебаний:
T 2
lпр.
I
2
g
mg l
По теореме
Штейнера:
I I с ml 2
I
I с ml 2 I с
lпр.
l l
ml
ml
ml

17.

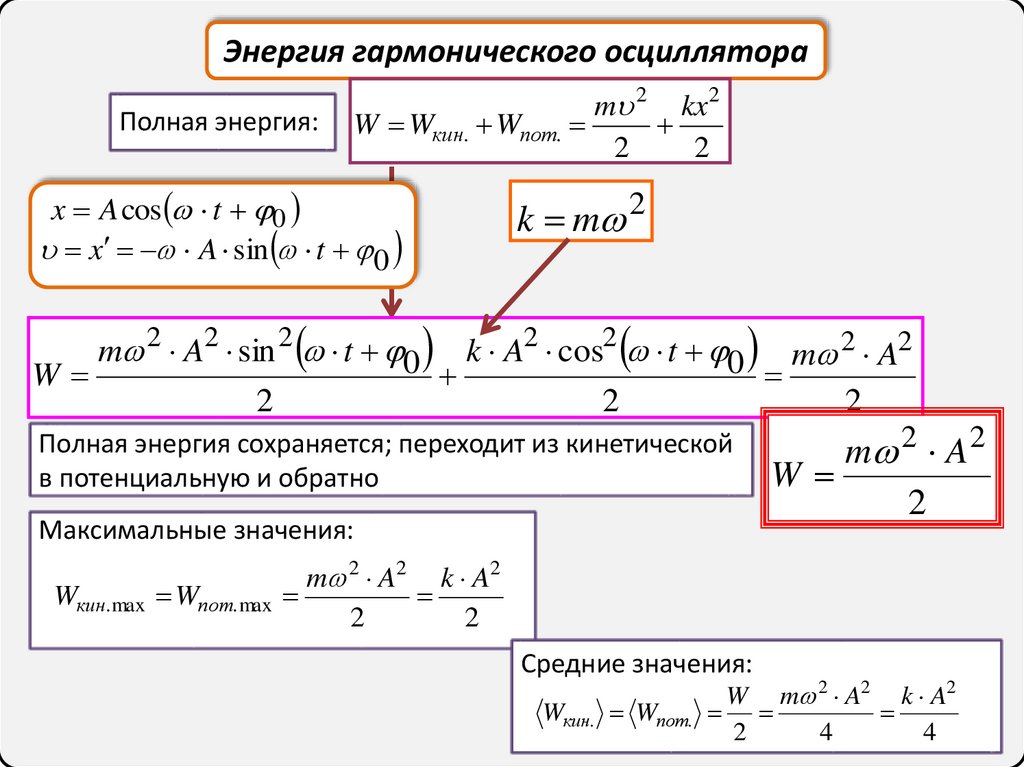
Энергия гармонического осциллятора
Полная энергия:
m 2 kx 2
W Wкин. Wпот.
2
2
x A cos t 0
x A sin t 0
k m 2
m 2 A2 sin 2 t 0 k A2 cos2 t 0 m 2 A2
W
2
2
2
Полная энергия сохраняется; переходит из кинетической
в потенциальную и обратно
Максимальные значения:
m 2 A 2
W
2
m 2 A2 k A2
Wкин. max Wпот. max
2
2
Средние значения:
W m 2 A2 k A2
Wкин. Wпот.
2
4
4

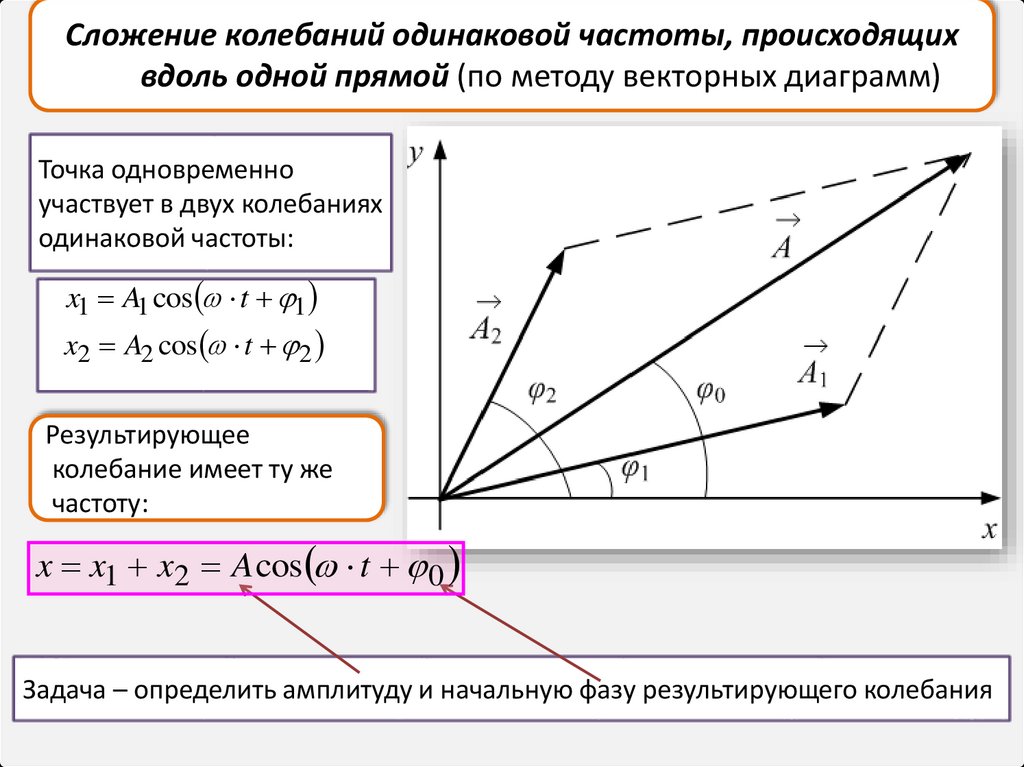
18.

Сложение колебаний одинаковой частоты, происходящих
вдоль одной прямой (по методу векторных диаграмм)
Точка одновременно
участвует в двух колебаниях
одинаковой частоты:
x1 A1 cos t 1
x2 A2 cos t 2
Результирующее
колебание имеет ту же
частоту:
x x1 x2 A cos t 0
Задача – определить амплитуду и начальную фазу результирующего колебания

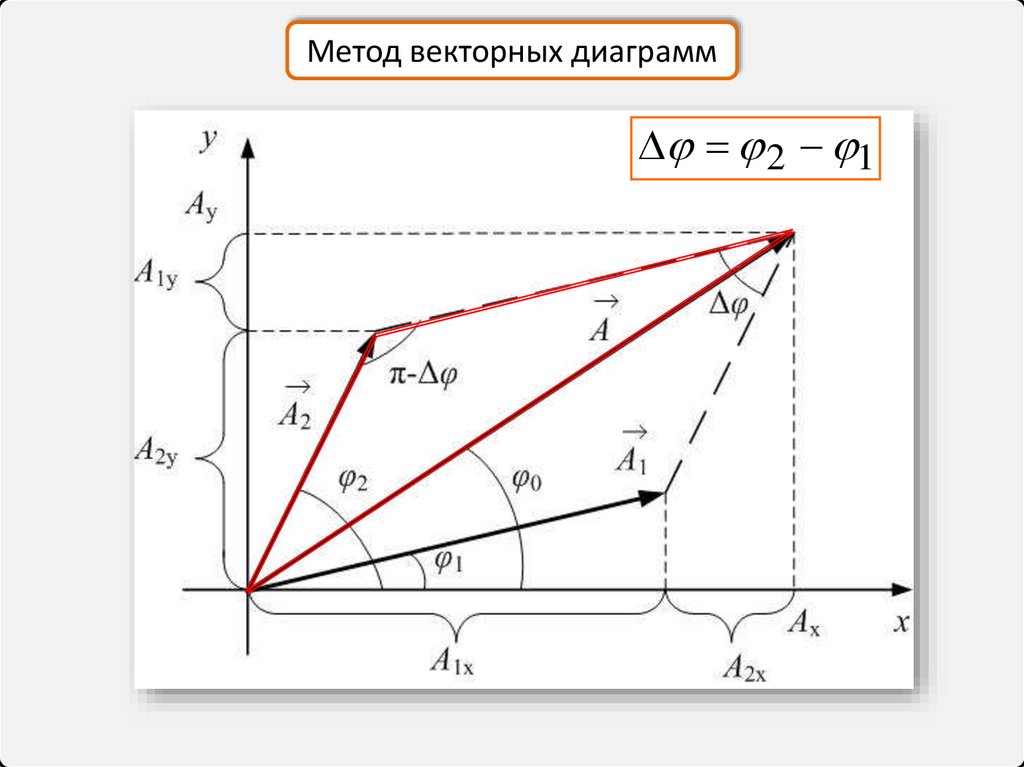
19.

Метод векторных диаграмм
2 1

20.

A A1 A2
Метод векторных диаграмм
Ax A1x A2 x
Ay A1 y A2 y
tg 0
Ay
Ax
A1 y A2 y
2 1
A1x A2 x
A sin 1 A2 sin 2
tg 0 1
A1 cos 1 A2 cos 2
По теореме косинусов:
A2 A12 A22 2 A1 A2 cos
A A12 A22 2 A1 A2 cos

21.

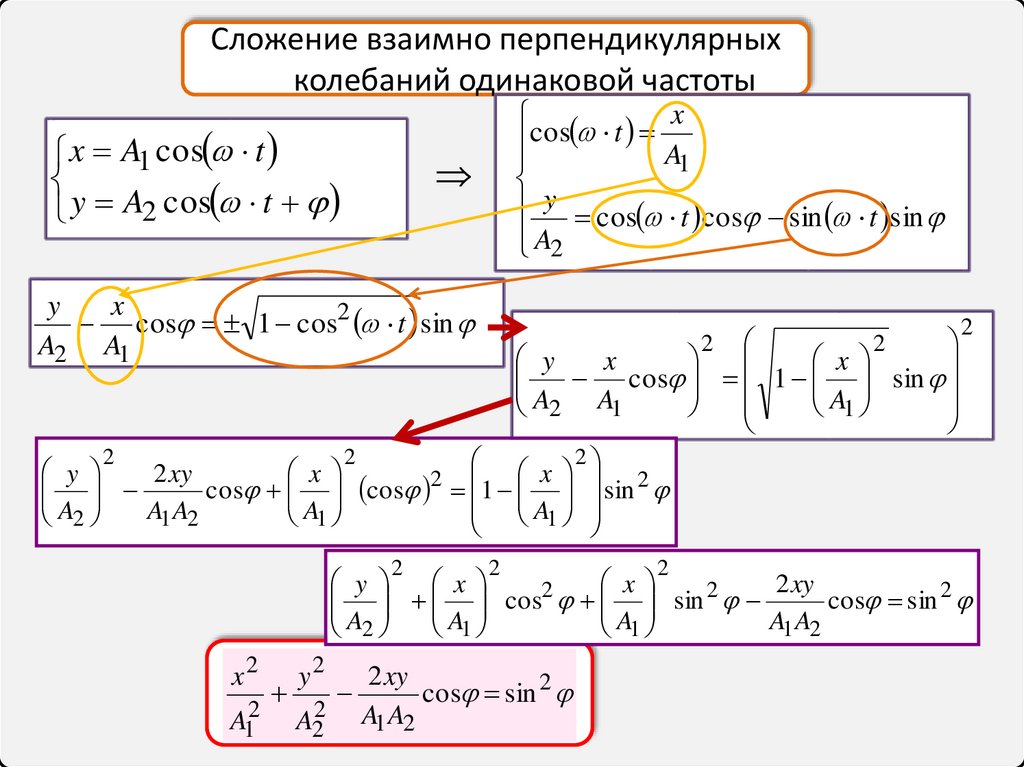
Сложение взаимно перпендикулярных
колебаний одинаковой частоты
x A1 cos t
y A2 cos t
x
cos t A
1
y cos t cos sin t sin
A2
y
x
cos 1 cos2 t sin
A2 A1
y
x
cos
A2 A1
2
2
x
1 sin
A1
2
2
2
x 2
y
x
2 xy
cos cos 2 1 sin 2
A1 A2
A1
A2
A1
2
2
2
y
x
x
2 xy
cos2 sin 2
cos sin 2
A1 A2
A2
A1
A1
x2
A12
y2
A22
2 xy
cos sin 2
A1 A2

22.

Сложение взаимно перпендикулярных
колебаний одинаковой частоты
x A1 cos t
y A2 cos t
x2
y2
2 xy
cos sin 2
A12 A22 A1 A2
В общем случае это уравнение эллипса:

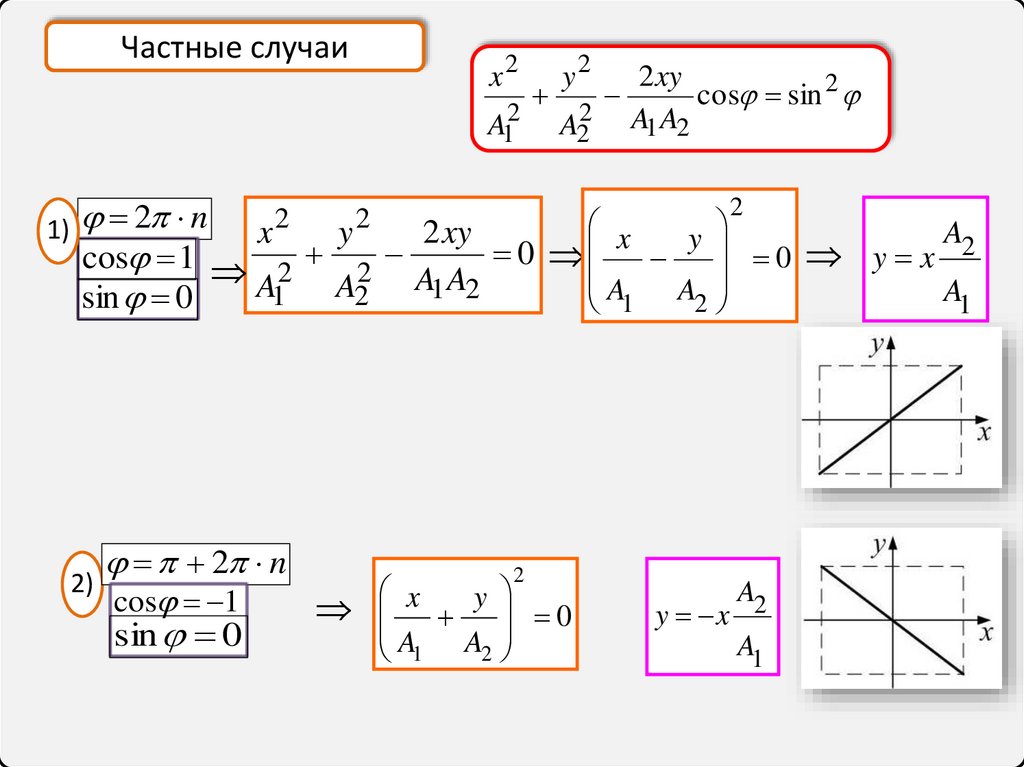
23.

Частные случаи
x2
A12
y2
A22
2 xy
cos sin 2
A1 A2
2
2
n
2
2
1)
A2
x
y
2 xy
x
y
0
0 y x
cos 1 2 2
A1 A2 A1 A2
A1
sin 0
A1 A2
2)
2 n
cos 1
sin 0
2
x
y
A A 0
1
2
y x
A2
A1

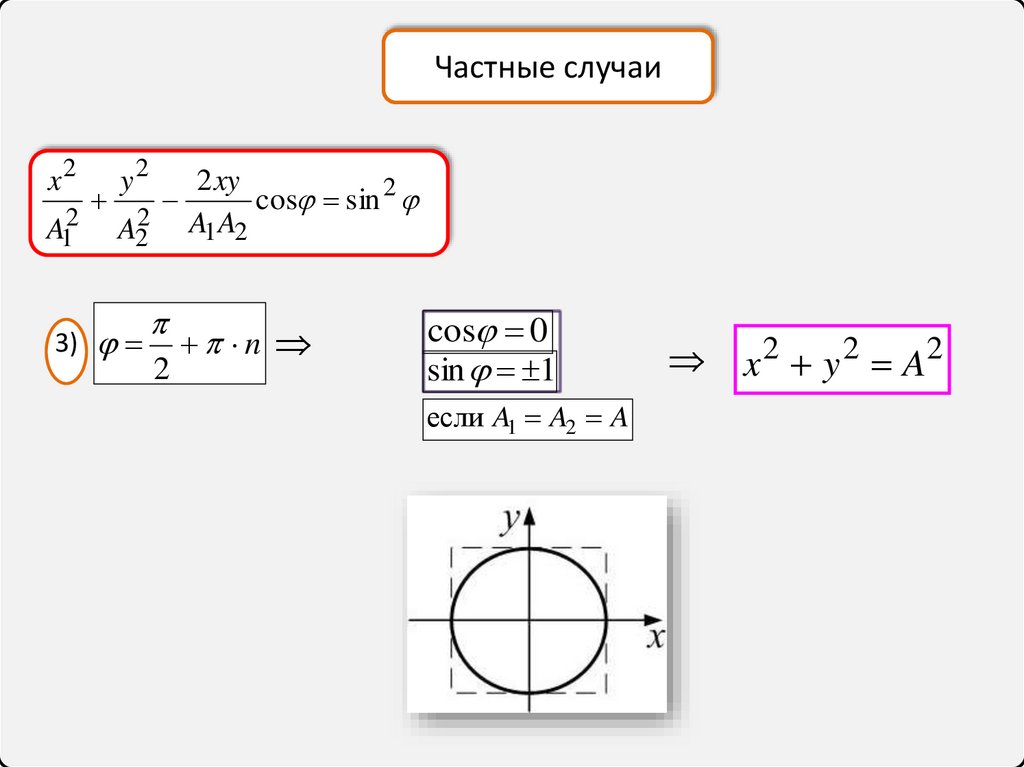
24.

Частные случаи
x2
A12
y2
A22
3)
2
2 xy
cos sin 2
A1 A2
n
cos 0
sin 1
если A1 A2 A
x 2 y 2 A2

25.

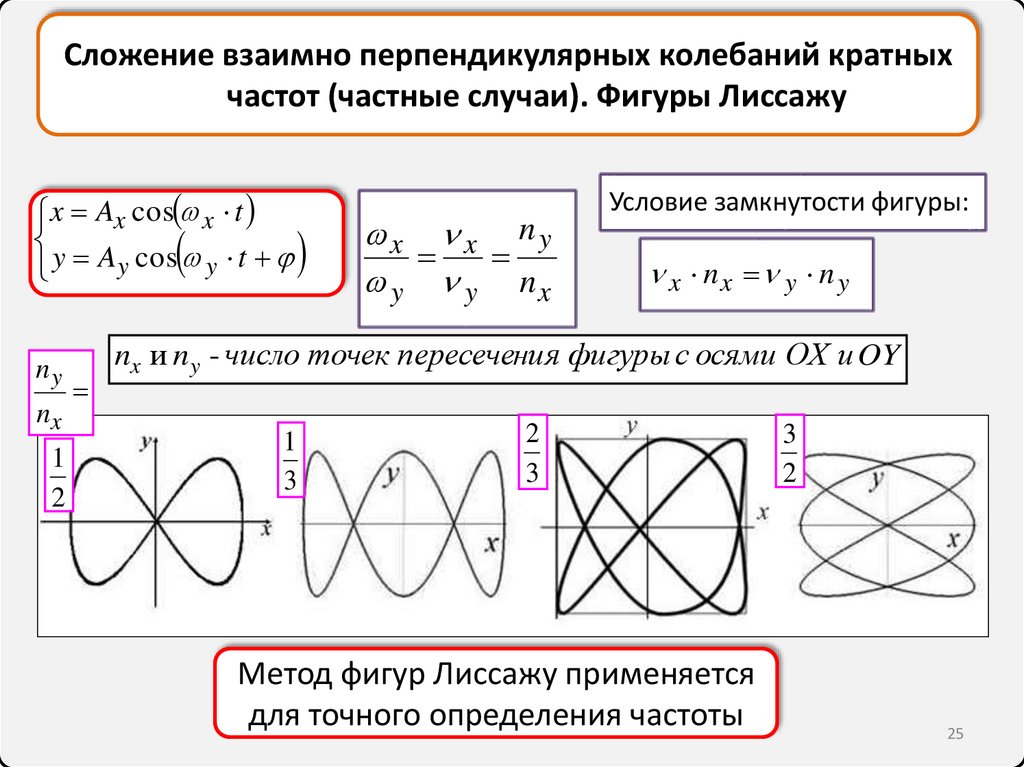
Сложение взаимно перпендикулярных колебаний кратных
частот (частные случаи). Фигуры Лиссажу
x Ax cos x t
y Ay cos y t
ny
nx
1
2
x x ny
y y nx
Условие замкнутости фигуры:
x nx y n y
nx и n y - число точек пересечения фигуры с осями OX и OY
1
3
2
3
Метод фигур Лиссажу применяется
для точного определения частоты
3
2
25

26.

Фигуры Лиссажу
На осциллографе:
https://youtu.be/hUu653khUlE
Запись песком:
https://youtu.be/rdWWvjH8cPM